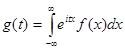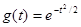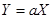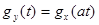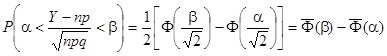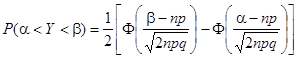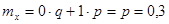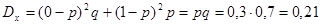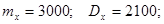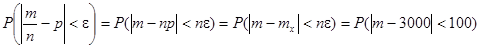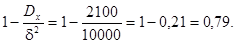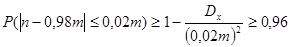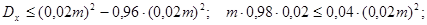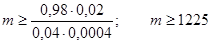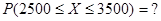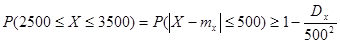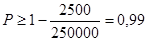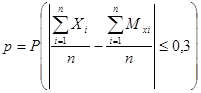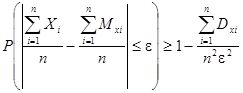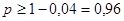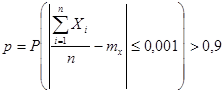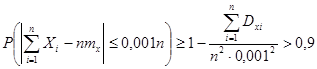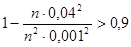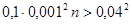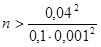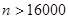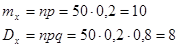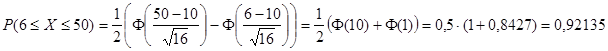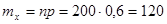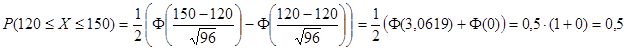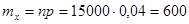вероятности того что произвольная деталь окажется бракованной в результате предварительного

Вероятность того, что деталь окажется бракованной, равна p. Составить закон распределения для случайной величины X – числа бракованных деталей в выборке объёма n. Определить вероятность того, что в вы

Готовое решение: Заказ №8392

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Теория вероятности

Дата выполнения: 30.09.2020

Цена: 208 руб.

Описание и исходные данные задания, 50% решения + фотография:

Вероятность того, что деталь окажется бракованной, равна p. Составить закон распределения для случайной величины X – числа бракованных деталей в выборке объёма n. Определить вероятность того, что в выборке будет бракованных:

1) ровно k деталей;

2) не более k деталей;

3) ни одна деталь не бракованная.

Найти F(х), математическое ожидание и дисперсию.

Решение.

где p = 0,6 – вероятность того, что деталь окажется бракованной;

q = 1 – p = 0,4 – вероятность того, что деталь окажется стандартной;

n = 3 – число деталей;

m = 0, 1, 2, 3 – число бракованных деталей среди трёх выбранных;

Составим закон распределения случайной величины X:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Презентация по решению задач по теории вероятностей

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Задачи на вероятность Левичева В.П., учитель математики МКОУ « Лодейнопольская СОШ №3 »

Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найти вероятность того,что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Решение: p=0,8∙0,8∙0,8∙(1-0,8)∙(1-0,8)=0,512∙0,2∙0,2=0,512∙0,04=0,02048

В барабане револьвера находятся 4 патрона из шести в произвольном порядке. Барабан раскручивают, после чего нажимают на спусковой крючок два раза. Найти вероятность двух осечек. Результат округлить до сотых. Решение Барабан раскручивают и нажимают на курок один раз, следовательно, p=2/6=1/3(2-число пустых, 6-число всех отверстий).Во второй раз р=1/5 (1-осталось пустых отверстий, 5-всех отверстий ).Тогда получим: Р=1/3∙1/5=1/15

Вероятность того, что взятая наугад деталь из некоторой партии деталей будет бракованной, равна 0,2.Найти вероятность того, что из трех взятых деталей две окажется не бракованными. Решение: Если вероятность того, что деталь бракованная, равна 0,2, то вероятность противоположного события : 1-0,2=0,8. Браком может быть деталь №1,№2,№3.Значит, Р=0,2∙0,8∙0,8+0,8∙0,2∙0,8+0,8∙0,8∙0,2=0,384

Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго-0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков. Решение: р=0,7∙(1-0,8)+0,8∙(1- 0,7)= 0,7∙0,2+0,8∙0,3= =0,14+0,24=0,38

В случайном эксперименте бросают две игральные кости. Найти вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. Решение: 1кубик: 2 3 4 5 6 2кубик: 6 3 4 3 2 значит, m=5, n=6∙6=36 тогда Р=5/36

Бросают два игральных кубика. Найти вероятность того, что в сумме выпадет четное число очков, не превосходящих шести. Решение: все равновозможные исходы при бросании двух кубиков: 1-1, 1-3, 2-2, 3-1,1-5, 2-4,3-3, 4-2,5-1.Значит,m=9. Так как бросают два кубика, то n=6∙6=36 Тогда вероятность p=m/n=9/36=0,25

Чему равна вероятность того, что при бросании трёх игральных костей 6 очков появится хотя бы на одной из костей? Решение: 3∙1/6∙5/6∙5/6+3∙1/6∙1/6∙5/6+1/6∙1/6∙1/6=91/216

0,42 Или 1-5/6∙5/6∙5/6=91/216=0,42 (Вероятность того, что не выпадет ни одной 6 или выпадет хотя бы одна 6 как вероятность противоположного события)

Перед началом первого тура чемпионата по настольному теннису участников разбивают на пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 спортсменов, среди которых 13 участников из России, в том числе Владимир Егоров. Найдите вероятность того, что в первом туре Владимир Егоров будет играть с каким-либо спортсменом из России. Решение: p=m/n=12/25=0,48

Два завода выпускают одинаковые автомобильные предохранители. Первый завод выпускает 40% предохранителей, а второй-60%.Первый завод выпускает 4% бракованных предохранителей,а второй-3%.Найдите вероятность того, что случайно выбранный предохранитель окажется бракованным. Решение:Н1-предохранитель с первого завода Н2-предохранитель со второго завода Р(Н1)=0,4 и Р(Н2)=0,6.Числа 0,04 и 0,03 являются условными вероятностями. Тогда Р=0,4∙0,04+0,6∙0,03=0,016+0,018=0,034

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Решение. Всего 4 варианта: о; о о; р р; р р; о. Благоприятных 2: о; р и р; о. Вероятность равна 2/4 = 1/2 = 0,5. Ответ: 0,5.

Задача 12 Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? Решение: Нужно учесть, что Руслан Орлов должен играть с каким-либо бадминтонистом из России. И сам Руслан Орлов тоже из России. Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна 9/25 = 36/100 = 0,36.

Задача 13 На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. Решение: Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: р = 0,2 + 0,15 = 0,35.

Задача 14 По отзывам покупателей Василий Васильевич оценил надёжность двух интернет ‐ магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,88. Василий Васильевич заказал товар сразу в обоих магазинах. Считая, что интернет ‐ магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар. Решение: Вероятность того, что первый магазин не доставит товар равна 1 − 0,8 = 0,2. Вероятность того, что второй магазин не доставит товар равна 1 − 0,88 = 0,12. Поскольку эти события независимы, вероятность их произведения (оба магазина не доставят товар) равна произведению вероятностей этих событий: 0,2· 0,12 = 0,024

Задача 16 Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнет игру с мячом. Команда «Олимпик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Олимпик» выиграет жребий ровно два раза. Решение: 3:8=0‚375 : № І 0 0 0 І І І І 0 № 2 0 І 0 0 І І 0 І № 3 0 0 І 0 І 0 І І

Агрофирма закупает куриные яйца в двух домашних хозяйствах. 55% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 35% яиц высшей категории. Всего высшую категорию получает 45% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства. Решение: Пусть x яиц из первого хозяйства,(1-x) из второго хозяйства. Тогда 0,55x+0,35(1-x)=0,45 0,55x-0,35x=0,1 0,2x =0,1 x=0,5 Ответ: 0,5

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах. Решение: Рассмотрим события А = кофе закончится в первом автомате, В = кофе закончится во втором автомате. Тогда A·B = кофе закончится в обоих автоматах, A + B = кофе закончится хотя бы в одном автомате. По условию P(A) = P(B) = 0,3; P(A·B) = 0,12. События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения: P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48. Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52. Задача 19

При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем – 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98? Решение: Можно решать задачу «по действиям», вычисляя вероятность уцелеть после ряда последовательных промахов: Р(1) = 0,6; Р(2) = Р(1) · 0,4 = 0,24; Р(3) = Р(2) · 0,4 = 0,096; Р(4) = Р(3) · 0,4 = 0,0384; Р(5) = Р(4) · 0,4 = 0,01536. Последняя вероятность меньше 0,02, поэтому достаточно пяти выстрелов по мишени. Задача 20

В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода Решение: Для погоды на 4, 5 и 6 июля есть 4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х – хорошая, О – отличная погода). Найдем вероятности наступления такой погоды: P(XXO) = 0,8 · 0,8 · 0,2 = 0,128; P(XOO) = 0,8 · 0,2 · 0,8 = 0,128; P(OXO) = 0,2 · 0,2 · 0,2 = 0,008; P(OOO) = 0,2 · 0,8 · 0,8 = 0,128. Указанные события несовместные, вероятность их сумы равна сумме вероятностей этих событий: P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = = 0,128 + 0,128 + 0,008 + 0,128 = 0,392. Задача 21

Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Задача 22 Решение : 0,52•0‚3= 0,156

Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов – математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов – математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку – 0,8, по иностранному языку – 0,7 и по обществознанию – 0,5. Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей. Таким образом, вероятность поступить хотя бы на одну из специальностей равна: 0,6∙0,8∙0,7∙0,5 + 0,6∙0,8∙0,3∙0,5 + 0,6∙0,8∙0,7∙0,5 = = 0,48∙0,35 + 0,48∙0,15 + 0,48∙0,35 = = 0,48∙(0,35 + 0,15 + 0,35) = 0,48∙0,85 = 0,408 Решение : Задача 23

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-172613

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Во Франции планируют ввести уголовное наказание за буллинг в школе

Время чтения: 1 минута

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Время чтения: 2 минуты

Апробацию новых учебников по ОБЖ завершат к середине 2022 года

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

34. Предельные теоремы

Как уже говорилось, при достаточно большом количестве испытаний, поставленных в одинаковых условиях, характеристики случайных событий и случайных величин становятся почти неслучайными. Это позволяет использовать результаты наблюдений случайных событий для предсказания исхода того или иного опыта.

Предельные теоремы теории вероятностей устанавливают соответствие между теоретическими и экспериментальными характеристиками случайных величин при большом количестве испытаний.

В рассмотренном выше законе больших чисел нечего не говорилось о законе распределения случайных величин.

Поставим задачу нахождения предельного закона распределения суммы

Когда число слагаемых П неограниченно возрастает. Эту задачу решает Центральная предельная теорема Ляпунова, которая была сформулирована выше.

В зависимости от условий распределения случайных величин Xi, образующих сумму, возможны различные формулировки центральной предельной теоремы.

Допустим, что случайные величины Xi взаимно независимы и одинаково распределены.

Теорема. Если случайные величины Xi Взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием т и дисперсией S2, причем существует третий абсолютный момент N3, то при неограниченном увеличении числа испытаний п закон распределения суммы 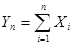неограниченно приближается к нормальному.

При доказательстве этой теоремы Ляпуновым использовались так называемые Характеристические функции.

Определение. Характеристической функцией случайной величины Х называется функция

эта функция представляет собой математическое ожидание некоторой комплексной случайной величины 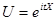, являющейся функцией от случайной величины Х. При решении многих задач удобнее пользоваться характеристическими функциями, а не законами распределения.

Зная закон распределения, можно найти характеристическую функцию по формуле (для непрерывных случайных величин):

Как видим, данная формула представляет собой не что иное, как преобразование Фурье для функции плотности распределения. Очевидно, что с помощью обратного преобразования Фурье можно по характеристической функции найти закон распределения.

Введение характеристических функций позволяет упростить операции с числовыми характеристиками случайных величин.

В случае нормального распределения характеристическая функция имеет вид:

Сформулируем некоторые свойства характеристических функций:

1) Если случайные величины Х И Y связаны соотношением

Где А – неслучайный множитель, то

2) Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых.

Случайные величины Xi, рассмотренные в центральной предельной теореме, могут обладать произвольными распределениями вероятностей.

Если все эти случайные величины одинаково распределены, дискретны и принимают только два возможных значения 0 или 1, то получается простейший случай центральной предельной теоремы, известный как Теорема Муавра – Лапласа.

Теорема. (Теорема Муавра – Лапласа) Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то для любого интервала (A, B) справедливо соотношение:

Где Y – число появлений события А в п опытах, Q = 1 – P, Ф(х) – функция Лапласа, 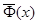— нормированная функция Лапласа.

Теорема Муавра – Лапласа описывает поведение бинОМинального распределения при больших значениях П.

Данная теорема позволяет существенно упростить вычисление по формуле биноминального распределения.

Расчет вероятности попадания значения случайной величины в заданный интервал 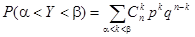при больших значениях П крайне затруднителен. Гораздо проще воспользоваться формулой:

Теорема Муавра – Лапласа очень широко применяется при решении практических задач.

Пример. Вероятность наступления события А в каждом испытании равна 0,3. Используя неравенство Чебышева, оценить вероятность того, что в 10000 испытаниях отклонение относительной частоты появления события А от его вероятности не превзойдет по абсолютной величине 0,01.

В соответствии с неравенством Чебышева вероятность того, что отклонение случайной величины от ее математического ожидания будет меньше некоторого числа e, ограничена в соответствии с неравенством .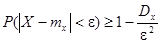

Надо определить математическое ожидание и дисперсию числа появления события А при одном опыте. Для события А случайная величина может принимать одно из двух значений: 1- событие появилось, 0- событие не появилось. При этом вероятность значения 1 равна вероятности Р=0,3, а вероятность значения 0- равна вероятности ненаступления события А

По определению математического ожидания имеем:

Дисперсия:

В случае П независимых испытаний получаем 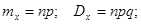Эти формулы уже упоминались выше.

В нашем случае получаем:

Вероятность отклонения относительной частоты появления события А в П испытаниях от вероятности на величину, не превышающую e=0,01 равна:

Выражение полученное в результате этих простых преобразований представляет собой не что иное, как вероятность отклонения числа Т появления события А от математического ожидания на величину не большую, чем d=100.

В соответствии с неравенством Чебышева эта вероятность будет не меньше, чем величина

Пример. Сколько следует проверить деталей, чтобы с вероятностью, не меньшей 0,96, можно было ожидать, что абсолютная величина отклонения относительной частоты годных деталей от вероятности детали быть годной, равной 0,98, не превысит 0,02.

Условие задачи фактически означает, что выполняется неравенство:

Здесь П— число годных деталей, Т— число проверенных деталей. Для применения неравенства Чебышева преобразуем полученное выражение:

После домножения выражения, стоящего в скобках, на Т получаем вероятность отклонения по модулю количества годных деталей от своего математического ожидания, следовательно, можно применить неравенство Чебышева, т. е. эта вероятность должна быть не меньше, чем величина 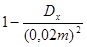, а по условию задачи еще и не меньше, чем 0,96.

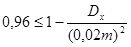
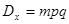
Таким образом, получаем неравенство . Как уже говорилось в предыдущей задаче, дисперсия может быть найдена по формуле .

Итого, получаем:

Т. е. для выполнения требуемых условий необходимо не менее 1225 деталей.

Пример. Суточная потребность электроэнергии в населенном пункте является случайной величиной, математическое ожидание которой равно 3000 кВт/час, а дисперсия составляет 2500. Оценить вероятность того, что в ближайшие сутки расход электроэнергии в этом населенном пункте будет от 2500 до 3500 кВт/час.

Требуется найти вероятность попадания случайной величины в заданный интервал:

Крайние значения интервала отклоняются от математического ожидания на одну и ту же величину, а именно – на 500. Тогда можно записать с учетом неравенства Чебышева:

Т. е. искомая вероятность будет не меньше, чем 0,99.

Пример. Среднее квадратическое отклонение каждой из 2500 независимых случайных величин не превосходит 3. Оценить вероятность того, что абсолютная величина отклонения среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий не превосходит 0,3.

Требуется найти вероятность

Неравенство Чебышева в случае суммы случайных величин имеет вид:

Если среднее квадратическое отклонение не превосходит 3, то, очевидно, дисперсия не превосходит 9. Величина e по условию задачи равна 0,3.

Тогда 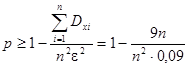. Отсюда получаем при N=2500:

Пример. Выборочным путем требуется определить среднюю длину изготавливаемых деталей. Сколько нужно исследовать деталей, чтобы с вероятностью, большей чем 0,9, можно было утверждать, что средняя длина отобранных изделий будет отличаться от математического ожидания этого среднего (средняя длина деталей всей партии) не более, чем на 0,001 см.? Установлено, что среднее квадратическое отклонение длины детали не превышает 0,04 см.

По условию если среднее квадратическое отклонение не превышает 0,04, то дисперсия, очевидно, не превышает (0,04)2. Также по условию задано, что

Если преобразовать соотношение, стоящее в скобках и после этого применить неравенство Чебышева, получаем:

Т. е. для достижения требуемой вероятности необходимо отобрать более 16000 деталей.

Описанный подход, как видно, позволяет решить множество чисто практических задач.

Пример. Вероятность того, что наудачу выбранная деталь окажется бракованной, при каждой проверке одна и та же и равна 0,2. Определить вероятность того, что среди 50 наугад выбранных деталей бракованных окажется не менее 6.

Фактически в задаче требуется определить вероятность того, что бракованных деталей будет не менее шести, но и, очевидно, не более 50- ти.

Значения функции Лапласа находятся по таблице. Конечно, значения функции Лапласа Ф(10) в таблице нет, но т. к. в таблицах указано, что Ф(3)=1,0000, то все значения от величин, превышающих 3 также равны 1. Дополнительно см. Функция Лапласа.

Пример. Известно, что 60% всего числа изготавливаемых заводом изделий являются изделиями первого сорта. Приемщик берет первые попавшиеся 200 изделий. Чему равна вероятность того, что среди них окажется из от 120 до 150 изделий первого сорта?

Вероятность того, что деталь окажется первого сорта, равна, очевидно, 0,6.

Математическое ожидание числа изделий первого сорта равно:

Пример. Проверкой установлено, что 96% изделий служат не меньше гарантируемого срока. Наугад выбирают 15000 изделий. Найти вероятность того, что со сроком службы менее гарантируемого будет от 570 до 630 изделий.

Вероятность того, что срок службы изделия будет менее гарантированного равна:

Математическое ожидание числа таких изделий равно

Источник