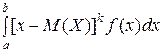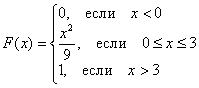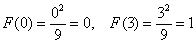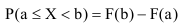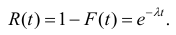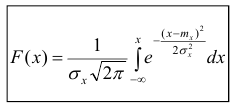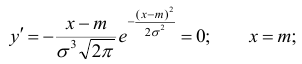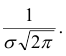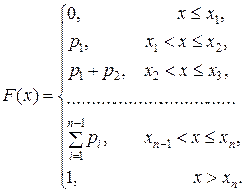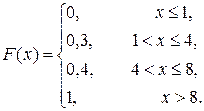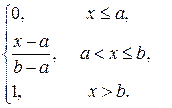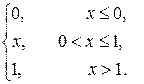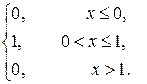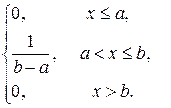вероятность того что непрерывная случайная величина примет точно заданное значение
2.4.1. Непрерывная случайная величина и её функция распределения
В отличие от дискретной случайной величины, НСВ может принять любое действительное значение из некоторого промежутка ненулевой длины, что делает невозможным её представление в виде таблицы (т.к. действительных чисел несчётно много). И посему непрерывную случайную величину задают функциями двух типов:
1) функцией распределения 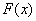
2) функцией плотности распределения 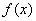
Начнём с функции распределения.
Как отмечалось ранее, функция распределения 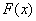
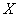
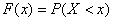
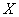
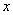
С увеличением 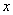
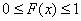
Важной особенностью непрерывного случая является тот факт, что функция распределения ЛЮБОЙ непрерывной случайной величины всюду непрерывна! Часто её можно встретить в кусочном виде, например:
однако в точках «стыка» всё хорошо:
и если там разрыв, то вы имеете дело с опечаткой или откровенной ошибкой!
! Но сама по себе непрерывность и ноль слева, единица справа – ещё не означают, что перед нами функция распределения.
При ручном построении чертежа целесообразно найти опорные точки; в нашем примере удобно взять: 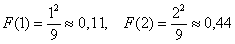
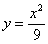
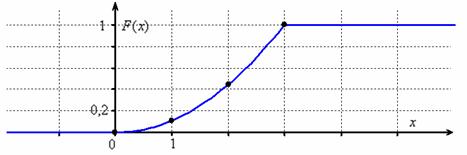
Напоминаю, что левый нижний луч следует прочертить жирно (чтобы он не сливался с осью), а правый верхний луч продолжить за остриё оси (т.к. график бесконечен). Функция распределения не можетубывать, и если вдруг окажется, что какой-то кусок графика идёт «сверху вниз», то ищите ошибку или опять же – имеет место опечатка. А может просто дрогнула рука 🙂
Что касаемо масштаба, то смотрим по ситуации, чаще всего оптимальный масштаб составляет 1 ед. = 1 см (две клетки), но поскольку я строю графики не от руки, то особо не слежу за пропорциями – в данном случае по оси ординат вышло примерно в 2 раза больше, чем по оси абсцисс.
Теперь вернёмся к смыслу функции распределения и рассмотрим пару конкретных значений 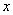
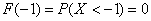
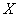
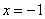
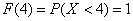
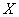
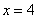
Ну и очевидно, что рассматриваемая случайная величина принимает случайные, наперёд неизвестные значения из отрезка 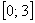
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Вероятность того что непрерывная случайная величина примет точно заданное значение
§ 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
3.3. Непрерывные случайные величины.
Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины:
Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х.
Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины.
Случайная величина 

 | (22) |
Функция 
Так как 
, то
 | (24) |
Пользуясь формулой (22), найдем 

 | (25) |
Заметим, что для непрерывной случайной величины функция распределения F(х) непрерывна в любой точке х, где функция 
На основании формулы (23), полагая x1=x, 
В силу непрерывности функции F(х) получим, что
Таким образом, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю.
Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств



Имеют одинаковую вероятность, т.е.
В самом деле, например,
так как
Замечание. Как мы знаем, если событие невозможно, то вероятность его наступления равна нулю. При классическом определении вероятности, когда число исходов испытания конечно, имеет место и обратное предложение: если вероятность события равна нулю, то событие невозможно, так как в этом случае ему не благоприятствует ни один из исходов испытания. В случае непрерывной случайной величины число возможных ее значений бесконечно. Вероятность того, что эта величина примет какое-либо конкретное значение x1 как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение x1. Поэтому в случае непрерывной случайной величины имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение.
Так, например, при изготовлении валика нас не интересует вероятность того, что его диаметр будет равен номиналу. Для нас важна вероятность того, что диаметр валика не выходит из поля допуска.
Пример. Плотность распределения непрерывной случайной величины задана следующим образом:

График функции 


Следующие два пункта посвящены часто встречающимся на практике распределениям непрерывных случайных величин — равномерному и нормальному распределениям.
Дальше. * Функция называется кусочно-непрерывной на всей числовой оси, если она на любом сегменте или непрерывна, или имеет конечное число точек разрыва I рода.
** Правило дифференцирования интеграла с переменной верхней границей, выведенное в случае конечной нижней границы, остается справедливым и для интегралов с бесконечной нижней границей. В самом деле,
Содержание:
Непрерывные случайные величины: функция распределения случайной величины:
Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.
Функция распределения непрерывной случайной величины
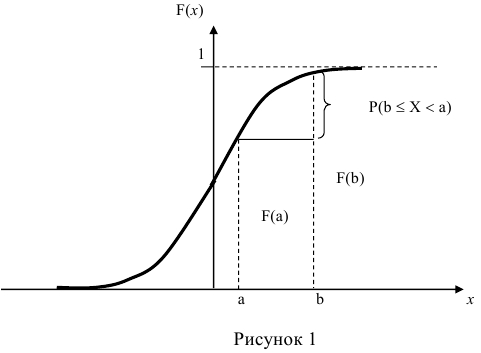
Зная функцию распределения непрерывной случайной величины, задача определения вероятности её попадания на интервал (а; b) может быть решена следующим образом.
По известной функции распределения вероятность попадания непрерывной случайной величины на интервал (а; b) равна приращению функции распределения на этом участке (рис. 1).
Во всех рассмотренных выше случаях случайная величина определялась путём задания значений самой величины и вероятностей этих значений.
Однако такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, её значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.
Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?
Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.
Функция надежности
Определение. Функцией надёжности R(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.
Часто на практике длительность безотказной работы подчиняется показательному закону распределению.
Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.
Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.
Функция надёжности для какого- либо устройства при показательном законе распределения равна:
Данное соотношение называют показательным законом надежности.
Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.
Таким образом, безотказная работа устройства зависит только от интенсивности отказов 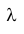
прошлом.
Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.
Нормальный закон распределения
Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.
Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
Можно легко показать, что параметры 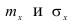
Найдём функцию распределения F(x).
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.
Нормальная кривая обладает следующими свойствами:
1) Функция определена на всей числовой оси.
2) При всех х функция распределения принимает только положительные значения.
3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента л\ значение функции стремится к нулю.
4) Найдём экстремум функции.
Т.к. при 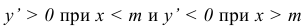
5) Функция является симметричной относительно прямой x = а, т.к. разность
6) Для нахождения точек перегиба графика найдем вторую производную функции плотности. 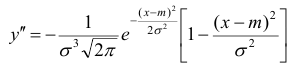
При 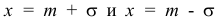
В этих точках значение функции равно 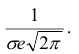
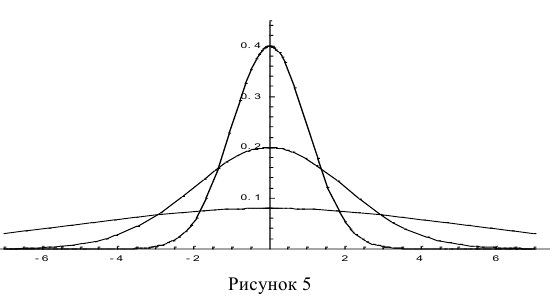
Построим график функции плотности распределения (рис. 5).
Построены графики при м =0 и трёх возможных значениях среднеквадратичного отклонения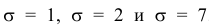
Если а > 0, то график сместится в положительном направлении, если а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Непрерывные случайные величины
( НСВ )
Непрерывной называют случайную величину, возможные значения которой непрерывно занимают некоторый интервал.
Если дискретная величина может быть задана перечнем всех её возможных значений и их вероятностей, то непрерывную случайную величину, возможные значения которой сплошь занимают некоторый интервал (а, b) задать перечнем всех возможных значений невозможно.
Следствие 1. Вероятность того, что случайная величина примет значение, заключённое в интервале (а, b), равна приращению функции распределения на этом интервале:
Следствие. Если возможные значения НСВ расположены на всей числовой оси ОХ (−∞, +∞), то справедливы предельные соотношения:
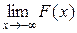
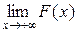
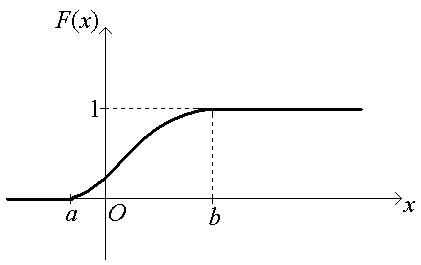
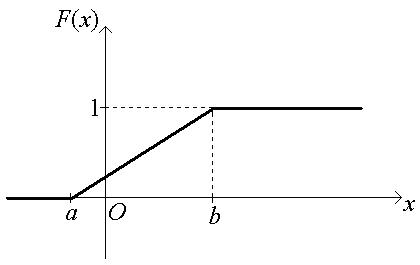
Рассмотренные свойства позволяют представить общий вид графика функции распределения непрерывной случайной величины:
Функцию распределения НСВ Х часто называют интегральной функцией.
Дискретная случайная величина тоже имеет функцию распределения:
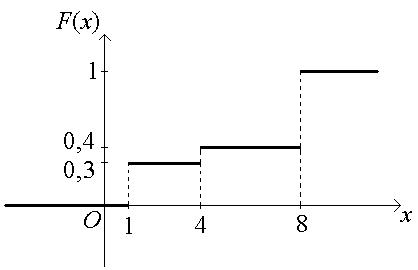
График функции распределения дискретной случайной величины имеет ступенчатый вид.
Пример. ДСВ Х задана законом распределения
Найти её функцию распределения и построить график.
Если 1 8, то F(x) = 1 (или F(x) = 0,3 + 0,1 + 0,6 = 1).
Итак, функция распределения заданной ДСВ Х:
График искомой функции распределения:
НСВ можно задать плотностью распределения вероятностей.
Плотностью распределения вероятностей НСВ Х называют функцию f(x) – первую производную от функции распределения F(x):
f(x) = 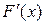
Функция распределения является первообразной для плотности распределения. Плотность распределения ещё называют: плотность вероятности, дифференциальной функцией.
График плотности распределения называют кривой распределения.
Теорема 1. Вероятность того, что НСВ Х примет значение, принадлежащее интервалу (а, b), равна определённому интегралу от плотности распределения, взятому в пределах от а до b:
Свойства плотности распределения:
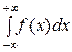
В частности, если все возможные значения случайной величины принадлежат интервалу (а, b), то
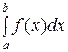
Пусть f(x) – плотность распределения, F(х) – функция распределения, тогда
F(х) = 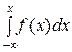
○ F(x) = Р(Х b, то F(х) = 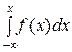
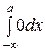
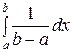
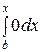
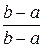
Итак, функция распределения имеет вид:
F(x) =
График искомой функции:
Числовые характеристики НСВ
Математическим ожиданием НСВ Х, возможные значения которой принадлежат отрезку [a, b], называют определённый интеграл
М(Х) = 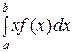
Если все возможные значения принадлежат всей оси ОХ, то
М(Х) = 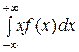
Предполагается, что несобственный интеграл сходится абсолютно.
Дисперсией НСВ Х называют математическое ожидание квадрата её отклонения.
Если возможные значения Х принадлежат отрезку [a, b], то
D(X) = 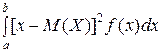
Если возможные значения Х принадлежат всей числовой оси (−∞; +∞), то
D(X) = 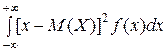
Легко получить для вычисления дисперсии более удобные формулы:
Среднее квадратическое отклонение НСВ Х определяется равенством
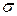
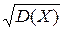
Замечание.Свойства математического ожидания и дисперсии ДСВ сохраняются и для НСВ Х.
Пример. Найти М(Х) и D(X) случайной величины Х, заданной функцией распределения
F(x) =
Найдём плотность распределения
f(x) = 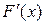
М(Х) = 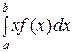
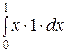
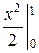
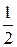
D(X) = 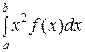
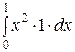
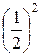
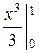
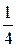
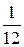
Пример (**).Найти М(Х), D(X) и 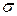
f(x) =
М(Х) = 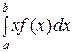
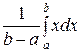
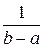
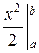
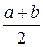
D(X) =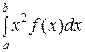
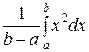
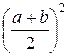
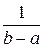
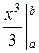
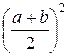
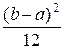
Найдем 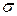
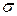
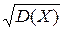
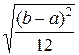
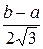
Теоретические моменты НСВ.
Начальный теоретический момент порядка k НСВ Х определяется равенством
νk = 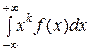
Центральный теоретический момент порядка k НСВ Х определяется равенством
μk = 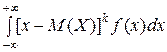
В частности, если все возможные значения Х принадлежат интервалу (a, b), то
νk = 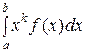
μk =