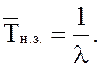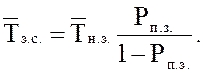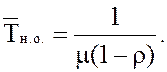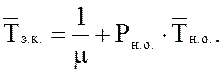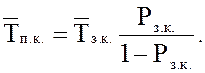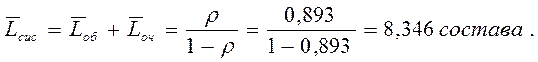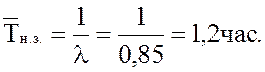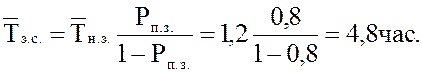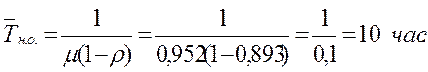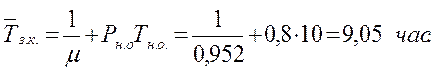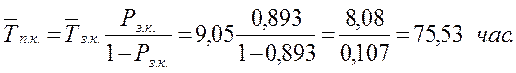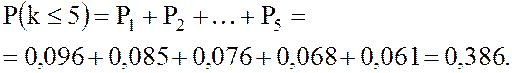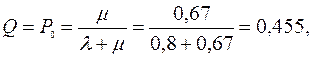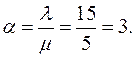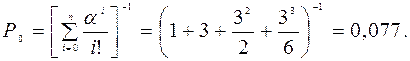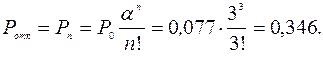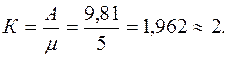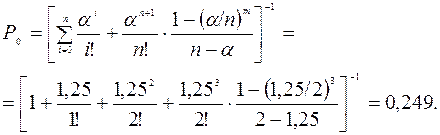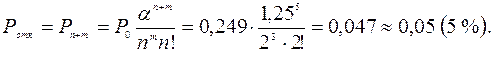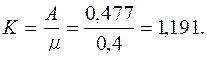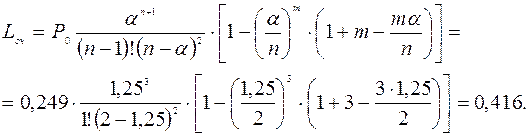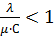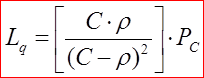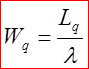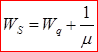вероятность того что канал обслуживания занят пункт разгрузки работает

Экономико-математические методы и модели (стр. 11 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

& Рекомендуемая литература: [1, 3–6, 9, 11].

4. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ

4.1. Постановка задачи

При исследовании операций часто приходится сталкиваться с системами, предназначенными для многоразового использования при решении однотипных задач. Возникающие при этом процессы получили название процессов обслуживания, а системы – систем массового обслуживания (СМО).

Главная особенность процессов массового обслуживания – случайность. При этом имеются две взаимодействующие стороны – обслуживаемая и обслуживающая.

Примерами процессов этого типа являются:

1) обслуживание покупателей в сфере розничной торговли;

2) транспортное обслуживание;

3) медицинское обслуживание населения;

4) ремонт аппаратуры, машин, механизмов, находящихся в эксплуатации;

5) обработка документов в системе управления;

6) туристическое обслуживание.

Неотъемлемой частью системы массового обслуживания является узел обслуживания, через который осуществляется взаимодействие входного и выходного потоков заявок. В случае транспортного обслуживания каналом может считаться отдельная единица транспортного средства.

Вид графической модели зависит как от числа каналов n, так и от допустимой длины очереди m. По указанным признакам различается ряд типов СМО, перечисленных в табл. 4.1.

Типы систем массового обслуживания

Одноканальная, без очереди

Многоканальная, без очереди

Многоканальная, с неограниченной очередью

По числу обслуживающих каналов различают одноканальные и многоканальные СМО.

Находящиеся в СМО заявки могут либо ожидать обслуживания, либо находиться под обслуживанием. Часть заявок, ожидающих обслуживания, образует очередь.

В зависимости от целочисленного значения m используются следующие названия в классификации типов СМО:

1) m = 0 – без очереди;

2) m > 0 – с очередью.

Если число мест в очереди m является конечным, то в СМО могут происходить отказы в предоставлении обслуживания некоторым заявкам. В связи с этим СМО указанного типа называются системами с отказами. Отклоняются от обслуживания те заявки, в момент прихода которых все места в очереди случайно оказались занятыми, или, если m = 0, все каналы оказались занятыми. Считается, что заявка, получившая отказ в обслуживании, навсегда теряется для СМО. Таким образом, пропускная способность СМО этого типа всегда меньше 100 %.

Если m не ограничено, что иногда условно записывают как m = , то соответствующая СМО называется системой с ожиданием. В СМО данного типа пришедшая заявка при отсутствии возможности немедленного обслуживания ожидает обслуживания, какой бы длинной ни были очередь и продолжительность времени ожидания.

4.2. Примеры решения задач систем массового обслуживания

Требуется решить задачи 1–3. Исходные данные приведены в табл. 4.2–4.4.

Некоторые обозначения, применяемые в теории массового обслуживания, для формул:

n – число каналов в СМО;

λ – интенсивность входящего потока заявок Пвх;

v – интенсивность выходящего потока заявок Пвых;

μ – интенсивность потока обслуживания Поб;

ρ – показатель нагрузки системы (трафик);

m – максимальное число мест в очереди, ограничивающее длину очереди заявок;

i – число источников заявок;

pк – вероятность k-го состояния системы;

pо – вероятность простаивания всей системы, т. е. вероятность того, что все каналы свободны;

pсист – вероятность принятия заявки в систему;

pотк – вероятность отказа заявке в принятии ее в систему;

роб – вероятность того, что заявка будет обслужена;

А – абсолютная пропускная способность системы;

Q – относительная пропускная способность системы;

оч – среднее число заявок в очереди;

об – среднее число заявок под обслуживанием;

сист – среднее число заявок в системе;

оч – среднее время ожидания заявки в очереди;

об – среднее время обслуживания заявки, относящееся только к обслуженным заявкам;

сис – среднее время пребывания заявки в системе;

ож – среднее время, ограничивающее ожидание заявки в очереди;

– среднее число занятых каналов.

Абсолютная пропускная способность СМО А – среднее число заявок, которое может обслужить система за единицу времени.

Относительная пропускная способность СМО Q – отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок.

При решении задач массового обслуживания необходимо придерживаться нижеприведенной последовательности:

1) определение типа СМО по табл. 4.1;

2) выбор формул в соответствии с типом СМО;

4) формулирование выводов по задаче.

Вариант выбирается следующим образом: две последние цифры зачетной книжки студента делятся с остатком на количество вариантов, представленных в таблицах. К остатку от деления прибавляется единица. Полученное число явится номером варианта для информации соответствующего вида.

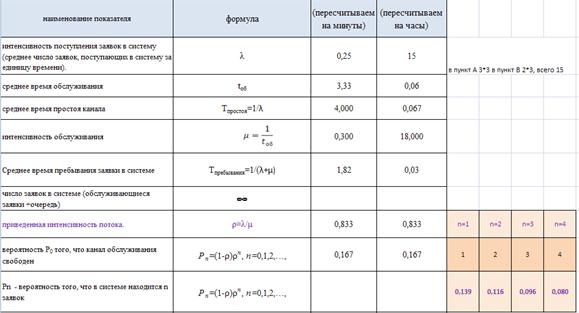
Задача 1. На сортировочную станцию прибывают составы с интенсивностью 0,9 состава в час. Среднее время обслуживания одного состава 0,7 часа. Определить показатели эффективности работы сортировочной станции: интенсивность потока обслуживаний, среднее число заявок в очереди, интенсивность нагрузки канала (трафик), вероятность, что канал свободен, вероятность, что канал занят, среднее число заявок в системе, среднее время пребывания заявки в очереди, среднее время пребывания заявки в системе (табл. 4.2).

Исходные данные для решения задачи 1

Источник

16. Вероятность того, что обслуживание ожидает не более ν заявок, т.е. в очереди будет не более ν заявок: .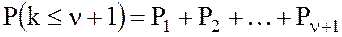

18. Среднее время неполной загрузки системы

19. Среднее время полной загрузки системы

20. Среднее время наличия очереди

22. Среднее время занятости канала

23. Среднее время простоя канала

Пример 7.— Железнодорожная сортировочная станция (ЖСС), на которую поступает простейший поток составов с интенсивностью λ = 0,85 состава/час, представляет собой одноканальную СМО с неограниченной очередью.

— Обслуживание (расформирование) состава длится случайное (показательное) время с₀ со средним значением 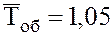час. Требуется:

1. Найти показатели эффективности СМО.

2. Построить граф состояний системы.

Решение.1. Интенсивность простейшего потока обслуживания или среднее число составов, обслуживаемых одним каналом за час при непрерывной его работе 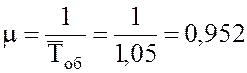составов/час.

2. Показатель нагрузки СМО .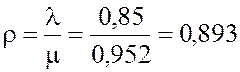

4. Вероятность любого состояния s_k СМО k = 1,2,…

Р₁ = (1 – ρ)∙ρ = (1-0,893)∙0,893 = 0,096;

Р₂ = (1 – ρ)∙ρ 2 = (1-0,893)∙0,893 2 = 0,085;

Р₃ = (1 – ρ)∙ρ 3 = (1-0,893)∙0,893 3 = 0,076;

Р₄ = (1 – ρ)∙ρ 4 = (1-0,893)∙0,893 4 = 0,068;

Р₅ = (1 – ρ)∙ρ 5 = (1-0,893)∙0,893 5 = 0,061 и т.д.

5. Вероятность того, что канал занят: Р_з.к. = 1 – Р₀ = ρ = 0,893.

6. Вероятность отказа в обслуживании состава Р_отк = 0.

7. Вероятность того, что пришедший состав будет принят в систему ЖСС: Р_сист = 1 – Р_отк = 1.

8. Относительная пропускная способность q = Р_сист = 1 – Р_отк = 1.

9. Абсолютная пропускная способность

A = λ∙q = λ∙1 = λ = 0,85 состава/час.

10. Среднее число составов, находящихся под обслуживанием:

.

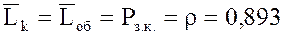
11. Среднее число составов, ожидающих очереди на расформирование (все равно, на каких путях): .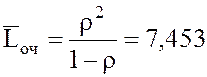

12. Среднее число составов, связанных со станцией:

13. Среднее время пребывания составов на очереди

час.

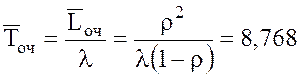
14. Среднее время (продолжительность) пребывания состава при станции (на внутренних, внешних путях и под обслуживанием)

час.

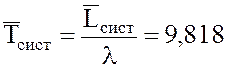
15. Среднее время обслуживания одного состава

час.

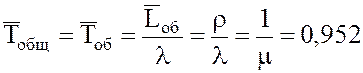
16. Среднее время неполной загрузки системы

17. Вероятность того, что система полностью загружена:

Р_п.з. = ρ 2 = (о,893) 2 = 0,8.

18. Среднее время полной загрузки системы

19. Среднее время наличия очереди

20. Вероятность наличия очереди в системе Р_н.о. = ρ 2 =0,8.

21. Среднее время занятости канала

22. Среднее время простоя канала

— Касса продает билеты в пунктах X и Y.

— Пассажиров, желающих купить билет в пункт Х, приходит в среднем трое за 20 мин., в пункт Y – двое.

— Поток пассажиров можно считать простейшим.

— Кассир в среднем обслуживает трех пассажиров за 10 мин.

— Время обслуживания распределяется по показательному закону, т.е. поток обслуживания простейший. Требуется:

Найти показатели эффективности СМО.

Решение.1. Среднее число пассажиров, желающих купить билет в пункт Х 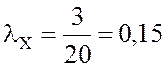заявки/мин.

2. Среднее число пассажиров, желающих купить билет в пункт У

заявки/мин.

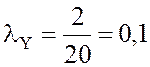
3. Общая интенсивность потока заявок 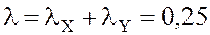заявки/мин.

4. Интенсивность потока обслуживания 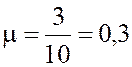заявки/мин.

5. Показатель нагрузки системы , это означает, что вероятности состояния системы существуют.

6. Р₀ = 1 – ρ = 1-0,833=0,167.

7. и т.д.

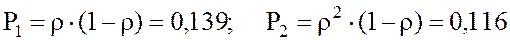
8. Вероятность того, что канал занят: Р_з.к. = 1 –Р₀ = ρ = 0,833,

12. A = λ∙q = 1∙0,25 = 0,25.

13. .

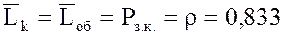
14. заявки.

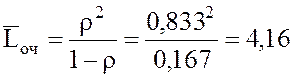
15. заявки.

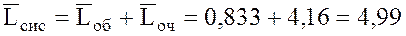
16. мин.

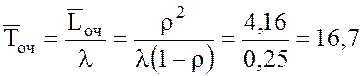
17. мин.

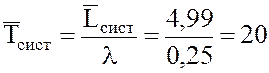
12.5.Многоканальная СМО с неограниченной очередью

— На m-канальную СМО поступает простейший поток заявок с интенсивностью λ = const.

— Поток обслуживаний также простейший с интенсивностью μ=const>0.

Источник

Примеры решения заданий

Пример 1.Телефонная АТС имеет одну линию, на которую в сред-
нем приходит 0,8 вызова в мин. Среднее время разговора 1,5 мин. Вызов, пришедший во время разговора, не обслуживается. Считая потоки вызовов пуассоновскими, найти абсолютную и относительную пропускную способности станции, вероятность отказа в обслуживании, а также среднее время пребывания заявки в системе.

Решение:

Телефонную станцию рассматриваем как одноканальную СМО с отказами. За единицу времени примем 1 мин.

Параметры системы следующие:

мин;

вызовов/мин.

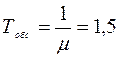
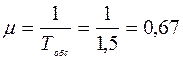
Рассчитаем относительную пропускную способность следующим образом:

т. е. в среднем обслуживается 45 % поступающих в систему заявок.

Абсолютная пропускная способность (интенсивность выходного потока заявок) равна:

A = lQ = 0,8 × 0,455 = 0,364 вызовов/мин.

мин.

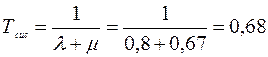
Пример 2.В отделении банка на обслуживании клиентов работают 3 оператора. Среднее время обслуживания одного клиента оператором – 12 мин. В среднем за час в банк обращаются 15 клиентов. Если все операторы заняты, клиенты не обслуживаются банком. Найти основные характеристики работы банка, а также вероятность того, что не менее двух каналов простаивают.

Решение:

Банк можно рассматривать как многоканальную СМО с отказами. За единицу времени примем 1 час.

Параметры системы равны:

клиентов/ч.

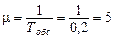
Рассчитаем параметр a по следующей формуле:

Вероятность того, что система свободна, определяется по формуле

Вероятность отказа в обслуживании равна

Относительная пропускная способность равна

Это означает, что из каждых 100 клиентов, обратившихся в банк, в среднем будут обслужены 65 клиентов. При этом абсолютная пропускная способность СМО составит следующую величину:

A = lQ = 15 × 0,654 = 9,81 клиентов/ч,

таким образом, банк обслуживает не 15 клиентов/ч, а меньше, что вызвано случайностью потока заявок.

Среднее число каналов, занятых обслуживанием заявок, вычисляется следующим образом:

Так как число каналов равно 3, а занято 2 канала, то это означает, что простаивает 1 канал.

Пример 3.В пункте обмена валюты работают два оператора, каждый их которых обслуживает клиента в среднем за 2,5 мин. По условиям безопасности в помещении пункта может находиться одновременно не более 5 человек, включая обслуживаемых клиентов. Если помещение заполнено, то очередной клиент не становится в очередь, а уходит. В среднем клиенты приходят каждые 2 мин. Найти основные характеристики работы обменного пункта.

Решение:

Математической моделью данного обменного пункта является двух-
канальная СМО (n = 2) с ожиданием и ограничением на длину очереди (m = 3). За единицу времени примем 1 мин.

Параметры системы следующие:

мин;

клиентов/мин;

клиентов /мин.

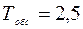
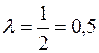
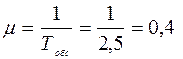
Рассчитаем параметр a следующим образом:

.

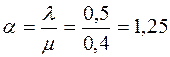
Вероятность того, что система свободна (оба канала свободны) равна

Вероятность отказа в обслуживании рассчитывается следующим образом:

Это означает, что из каждых 100 клиентов, обратившихся в пункт, в среднем будут обслужены около 95 человек.

Относительная пропускная способность рассчитывается следующим образом:

Абсолютная пропускная способность равна

A = l× Q = 0,5 × 0,953 = 0,477 клиентов/мин,

т. е. из обменного пункта в среднем выходят 0,48 клиентов/мин.

Среднее число каналов, занятых обслуживанием заявок, вычисляется по формуле

Средняя длина очереди рассчитывается следующим образом:

Среднее число заявок, находящихся в системе равно

Среднее время ожидания заявки в очереди равно

мин.

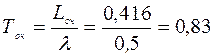
Среднее время пребывания заявки в системе равно

мин.

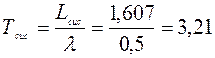
Пример 4. В кассе метрополитена, продающей карточки на проезд, работают два окна. В среднем один кассир тратит на обслуживание одного пассажира 0,5 мин. В среднем к кассе подходит 3 человека в мин. Найти основные характеристики работы кассы.

Решение:

Касса метрополитена моделируется двухканальной СМО с ожиданием и без ограничения на длину очереди. За единицу времени примем 1 мин.

Параметры системы следующие:

мин;

чел/мин;

чел/мин.

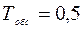
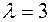
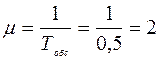
Рассчитаем параметр 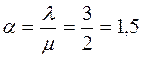и проверим выполнение условия a/n

Источник

Многоканальная СМО с ожиданием

Входной и выходной потоки имеют интенсивности λ и μ соответственно, параллельно обслуживаться могут не более С клиентов, то есть система имеет С каналов обслуживания.

Средняя продолжительность обслуживания одного клиента равна 1/µ.

Вероятности того, что в системе находятся п заявок (С обслуживаются, остальные ожидают в очереди) равна:

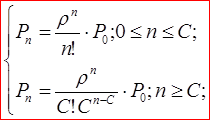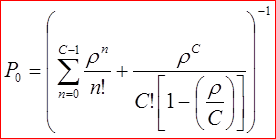Решение будет действительным, если выполняется следующее условие:

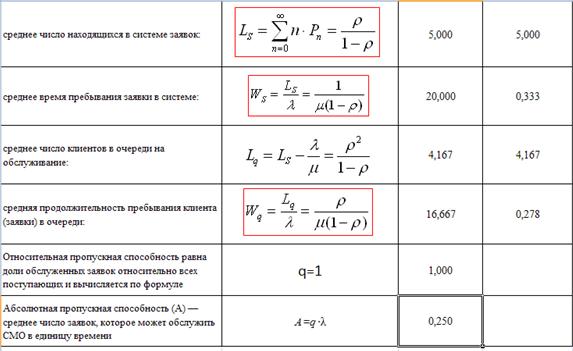
Остальные вероятностные характеристики функционирования в стационарном режиме многоканальной СМО с ожиданием и неограниченной очередью определяется по следующим формулам:
среднее число заявок в очереди на обслуживание

среднее число находящихся в системе заявок (на обслуживание и в очереди)
L_S=L_q+ρ;
средняя продолжительность пребывания заявки в очереди (заявки на обслуживание)

средняя продолжительность пребывания клиента в системе

Рассмотрим примеры многоканальной системы массового обслуживания с ожиданием.

Задача 4.5.:. Дана СМО с тремя каналами. Интенсивность потока λ=2,5 заявок в сутки, среднее время обслуживания одной заявки распределено по показательному закону и равно t_об=0,5 сут. Очередь заявок может расти практически неограниченно.
Требуется вычислить следующие предельные значения вероятностных характеристик системы:
— вероятность состояний системы;
— среднее число заявок в очереди на обслуживание;
— среднее число находящихся в системе заявок;
— среднюю продолжительность пребывания заявки в очереди;
— среднюю продолжительность пребывания заявки в системе.

Решение

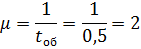
ρ=λ/μ=2,5/2,0=1,25,
λ/μ ∙с=2,5/2∙3=0,41

Пассажиров, желающих купить билет в пункт А, приходит в среднем трое за 20 мин, в пункт В — двое за 20 мин. Поток пассажиров простейший.

Кассир в среднем обслуживает трех пассажиров за 10 мин. Вычислить среднее число заявок в системе и в очереди, среднее время пребывания заявки в системе, среднее время пребывания заявки в очереди.

Контрольная работа к лекции 4. Элементы теории массового обслуживания. (выполнение не обязательно даже на оценку «отлично». Только для ознакомления)

1. Междугородный аэропорт предполагает открыть четыре пропускных терминала. В среднем за сутки поступает 320пассажиров. Средняя длительность проверки составляет 5мин. Длина очереди не должна

превышать 6 пассажиров. Определить вероятность простоя каналов, вероятность отказа, вероятность обслуживания, среднее число занятых каналов, среднее число заявок в очереди, среднее число заявок в системе, абсолютную

пропускную способность, относительную пропускную способность, среднее

время заявки в очереди, среднее время заявки в системе, среднее время заявки под обслуживанием).

2. В отделение сбербанка для оплаты коммунальных услуг и др. счетов 9-10 числа каждого месяца заходит в среднем 28 человек в час(примем, что этот поток приблизительно постоянен в течение всего рабочего времени кассы). Опыт показывает, что оператор тратит в среднем 4 мин на человека.

— Сколько Вы бы задействовали операторов (окошек), чтобы обслужить этот

— Как Вы оцениваете, будет ли при этом очередь? Сколько людей будет ожидать обслуживания (в среднем)?

— Как Вы оцениваете, сколько примерно времени (в среднем) каждый посетитель будет проводить в сберкассе для оплаты своих счетов?

3. В газете бесплатных объявлений имеются 4 телефонные линии, на которых работают 4 оператора. В редакцию газеты в среднем звонит 1 клиент в минуту и попадает автоматически на любую свободную линию. Время обслуживания клиента в среднем составляет 3 минуты. Сколько в среднем клиентов за час обслужат операторы?

4. В газете бесплатных объявлений имеются 3 телефонные линии, на которых работают 3 оператора. В редакцию газеты в среднем звонит 1 клиент в минуту и попадает автоматически на любую свободную линию. Время обслуживания клиента в среднем составляет 2 минуты. Сколько в среднем клиентов за час обслужат операторы?

5. Среднее время обслуживания клиента в магазине –одна минута. В среднем магазин посещает тридцать человек в час. Какая вероятность того, что при долгой работе магазина в очереди будет находиться три человека.
Задания по вариантам.

6. В киоске одно торговое место. Средний поток покупателей – 50 человек в час. Среднее время обслуживания покупателя – 2 минуты. Если очередной подошедший покупатель обнаруживает, что кто-то уже обслуживается, то он переходит к соседнему киоску. Время работы киоска – 12 часов в день. Каждый покупатель в среднем приносит прибыль киоску 10 рублей. Определить среднюю ежедневную прибыль киоска. На сколько возрастет прибыль, если в киоске открыть второе торговое место.

7. В магазине имеются 3 продавца, каждый обслуживает в среднем покупателя 10 минут. Если все они заняты, то образуется очередь, длина которой не превышает 2 человека. В магазин приходит в среднем 15 посетителей в час. Сколько посетителей в час в среднем обслуживается.

8. В газете бесплатных объявлений имеются 4 телефонные линии, на которых работают 4 оператора. В редакцию газеты в среднем звонит 1 клиент в минуту и попадает автоматически на любую свободную линию. Время обслуживания клиента в среднем составляет 3 минуты. Сколько в среднем клиентов за час обслужат операторы?

9.В газете бесплатных объявлений имеются 3 телефонные линии, на которых работают 3 оператора. В редакцию газеты в среднем звонит 1 клиент в минуту и попадает автоматически на любую свободную линию. Время обслуживания клиента в среднем составляет 2 минуты. Сколько в среднем клиентов за час обслужат операторы?

10.Пусть одноканальная СМО с отказами представляет собой один пост ежедневного обслуживания для мойки автомобилей. Заявка — автомобиль, прибывший в момент, когда пост занят, — получает отказ в обслуживании. Интенсивность потока автомобилей λ=2 (автомобиль в час). Средняя продолжительность обслуживания — t_об=0,8 часа. Требуется определить в установившемся режиме предельные значения: относительной пропускной способности q; абсолютной пропускной способности А; вероятности отказа Р_отк. Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый автомобиль обслуживался точно 0,8 часа и автомобили следовали один за другим без перерыва.

11.Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограниченно и равно 5. Если все стоянки заняты, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику имеет интенсивность λ=3 (автомобиля в час). Время диагностики автомобиля в среднем равно t=0,5 час. Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.

12. Среднее время обслуживания клиента в магазине – одна минута. В среднем магазин посещает тридцать человек в час. Какая вероятность того, что при долгой работе магазина в очереди будет находиться три человека.

Лекция 7. Модели производства и потребления (конспект необязателен. Только для ознакомления)

Модели производства строятся с помощью производственных функций, а модели потребления на основе целевой функции потребления.

Источник