вероятность события а при условии что произошло событие в называется
2.05. Условная вероятность. Вероятность произведения событий
Определение 2.2. Вероятность события А, Вычисленная при условии, что произошло событие В, Называется Условной вероЯтностью события А при наличии события В И обозначается Р(А|В).
Пример 2.10. Опыт: подбрасывание двух монет. События:
Найти вероятность Р(А). Общее число возможных исходов опыта N=4 (Оо, Ор, рр, ро), благоприятствующий исход один (оо), следовательно, Р(А)=1/4.
Найти теперь условную вероятность Р(А|В). Поскольку известно, что произошло событие В, Число возможных исходов испытания П–1 (оо, ор, ро), благоприятствующий исход по–прежнему один, следовательно, Р(А|В)=1/3.
Теорема. Вероятность произведения двух событий А И В, Равна произведению вероятности одного из этих событий на условную вероятность другого при наличии первого:
Эта теорема обобщается на любое конечное число событий следующим образом:

Определение 2.3. Два события называются независимыми, если появление любого из них не изменяет вероятности другого, т. е. события А И В Независимы, если Р(А|В)=Р(А).
Из формул (2.1) следует, что если выполняется равенство Р(А|В)=Р(А),.То выполняется и равенство Р(В\А)=Р(В).
Пример 2.11. Из урны, содержащей 3 белых и 7 черных шаров, наудачу извлекают два шара. Найти вероятность того, что оба шара белые.
Решение. Считаем, что шары извлекаются поочередно. Пусть
Пример 2.12. Два стрелка стреляют по одной мишени. Вероятность поражения мишени первым стрелком равна 0.6, вторым – 0.8. Найти вероятность того, что в мишени будет две пробоины.
Решение. Введем в рассмотрение события, вероятности которых известны:
Интересующее нас событие выразим через эти события. Для того, чтобы имело место событие С=<две пробоины в мишени>, надо, чтобы произошли вместе события А И В, Т. е. С=АВ.
Естественно считать события А И В Независимыми, поэтому
Математика — онлайн помощь
Случайное событие определяется как событие, которое при осуществлении определенного комплекса условий S может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий S не налагается, то такую вероятность называют безусловной, если же налагаются другие дополнительные условия, то вероятность называют условной. Например, часто приходится вычислять вероятность одного события при дополнительном условии, что произошло другое событие.
Пусть А и В – наблюдаемые события в испытании.
Условной вероятностью Р(В/А) наступления события В при условии, что событие А произошло в результате испытания, называется величина определяемая равенством 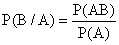
Аналогично определяется условная вероятность Р(А/В)
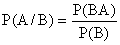
Основанием для подобного введения условной вероятности служит свойство 5, справедливое для статистического и классического определения вероятности.
ПРИМЕР 13.1.12 В урне 3 белых и 2 красных шара. Из урны последовательно без возвращения извлекают два шара (испытание). Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен красный шар (событие А).
Решение. После первого испытания, когда произошло событие А, в урне осталось 4 шара, из них 3 белых.
Искомая условная вероятность равна 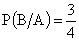
Определим теперь 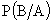
Вероятность появления красного шара в первом испытании 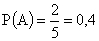
Найдем вероятность 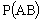
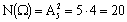
При этом событию 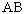
Следовательно, 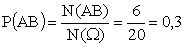
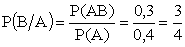
Как и следовало ожидать, ответ получился такой же, как и при непосредственном вычислении.
Теоремы умножения вероятностей
Из формул (13.1.10), (13.1.11) получается теорема умножения вероятностей для зависимых событий. Случайные события называются зависимыми, если вероятность наступления одного из них зависит от того, имело место или нет другое событие. Если для примера 13.1.12 в первом испытании наступило бы событие А (извлечен не красный, а белый шар), то
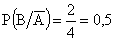
Следовательно, событие В зависит от события А.
ТЕОРЕМА 13.1.1 Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.
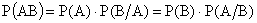
ПРИМЕР 13.1.13 Вероятность попадания ракеты в цель (событие А) 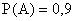
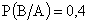
Решение. Событие АВ – ракета попала в цель и цель поражена.
По теореме 13.1.1: 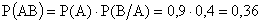
Теорему 13.1.1 можно обобщить на случай любого числа событий.
ТЕОРЕМА 13.1.2 Вероятность произведения нескольких событий равна произведению вероятности одного из них на условные вероятности остальных событий, причем вероятность каждого последующего события вычисляется в предположении, что предыдущие события уже наступили.
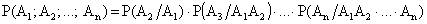
В частности, для трех событий:
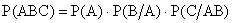
Событие А называется независимым от события B, если выполняется условие
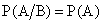
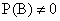
Если событие А не зависит от события В, то и событие В не зависит от события А, что следует из формулы (13.1.13) с учетом формулы (13.1.15): 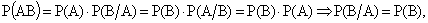
где 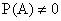
Это означает, что свойство независимости событий взаимно.
События А и В называются независимыми, если 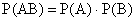
Формула (13.1.17) выражает теорему умножения для независимых событий.
Теорема 13.1.3 Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
События 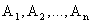
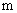
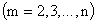
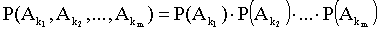
ТЕОРЕМА 13.1.4 Вероятность произведения нескольких независимых в совокупности событий равна произведению вероятностей этих событий: 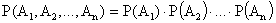
Независимость событий
Формулы (13.1.17), (13.1.18) позволяют установить независимость (зависимость) событий, если известны вероятности всех нужных событий. На практике независимость событий обычно устанавливают из физических соображений.
ПРИМЕР 13.1.14 Два стрелка производят по одному выстрелу по цели. Вероятность попадания в цель для первого стрелка (событие А1) 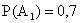
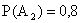
Чему равна вероятность того, что оба стрелка попадут в цель?
Решение. События 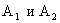
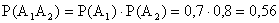
Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Полная вероятность и формула Байеса
п.1. Зависимые события и условные вероятности
Чтобы вспомнить о сложении и умножении вероятностей и независимых событиях – см. §39 справочника для 9 класса.
Напомним, что два случайных события A и B называют независимыми, если наступление одного из них не изменяет вероятность наступления другого.
Например: при бросании монеты несколько раз каждый следующий бросок совершенно не зависит от предыдущих.
Например:
Рассмотрим урну, в которой находится 3 белых и 3 черных шара.
Мы достаем шары, смотрим на их цвет и не возвращаем их на место. События в последовательности становятся зависимыми.
Пусть событие A=»в 1й раз достаем черный шар»,
Событие B=»во 2й раз достаем белый шар»
Событие C=»во 2й раз достаем черный шар»
После того, как произошло событие A, в урне остается 3 белых и 2 черных шара.
Тогда условная вероятность для события B при условии, что событие A произошло:
\(P(B|A)=\frac35\)
Аналогично, условная вероятность для события C:
\(P(B|A)=\frac25\)
п.2. Вероятность совместного появления событий
п.3. Формула полной вероятности
| i | Класс | К-во учеников | \(P(B_i)\) | К-во знатоков | \(P(A|B_i)\) | \(P(B_i)\cdot P(A|B_i)\) |
| 1 | 11A | 35 | 35/100=0,35 | 10 | 10/35=2/7 | 0,1 |
| 2 | 11Б | 35 | 35/100=0,35 | 7 | 7/35=1/5 | 0,07 |
| 3 | 11В | 30 | 30/100=0,3 | 10 | 3/30=1/10 | 0,03 |
| Всего | 100 | 1 | 20 | × | 0,2 | |
Получаем полную вероятность \(P(A)=\sum_
В данном случае ответ можно получить и проще: 20 знатоков на 100 человек дает \(P(A)=0,2\).
п.4. Формула Байеса
п.5. Примеры
Пример 1. Двигатель работает в трех режимах: нормальном (65% времени), форсированном (25% времени) и холостом. Вероятность поломки в каждом из режимов соответственно равна \(p_1=0,1;\ p_2=0,8;\ p_3=0,05\).
а) найдите вероятность поломки двигателя во время работы;
б) двигатель сломался. Какова вероятность, что он в этот момент работал в форсированном режиме?
| i | Режим | Часть времени \(P(B_i)\) | Вероятность поломки \(P(A|B_i)\) | \(P(B_i)\cdot P(A|B_i)\) |
| 1 | Нормальный | 0,65 | 0,1 | 0,065 |
| 2 | Форсированный | 0,25 | 0,8 | 0,2 |
| 3 | Холостой | 0,1 | 0,05 | 0,005 |
| Всего | 1 | × | 0,27 | |
Ответ: a) 0,27; б) \(\frac<20><27>\approx 0,741\)
Пример 2. В состязании лучников участвуют три стрелка. Вероятность попадания в мишень для каждого из них равна 0,3; 0,5 и 0,7. Один из стрелков стреляет и не попадает. Какова вероятность, что это был:
а) первый стрелок;
б) второй стрелок;
в) третий стрелок;
| i | \(P(B_i)\) | Вероятность промаха \(P(A|B_i)\) | \(P(B_i)\cdot P(A|B_i)\) |
| 1 | \(\frac13\) | 1-0,3=0,7 | \(\frac13\cdot 0,7=\frac<7><30>\) |
| 2 | \(\frac13\) | 1-0,5=0,5 | \(\frac13\cdot 0,5=\frac<1><6>\) |
| 3 | \(\frac13\) | 1-0,7=0,3 | \(\frac13\cdot 0,3=\frac<1><10>\) |
| ∑ | 1 | × | 0,5 |
Пример 3. Три фрилансера на площадке выполняют заказы в отношении по количеству 3:4:3. Доля успешно выполненных заказов для каждого из них составляет 98%, 95% и 90%.
а) найдите вероятность успешного выполнения заказа на площадке;
б) найдите вероятность неуспеха на площадке;
в) кто из фрилансеров, вероятнее всего, виноват в неуспешной работе?
| i | \(P(B_i)\) | Вероятность успеха \(P(A|B_i)\) | \(P(B_i)\cdot P(A|B_i)\) |
| 1 | 0,3 | 0,98 | 0,294 |
| 2 | 0,4 | 0,95 | 0,38 |
| 3 | 0,3 | 0,9 | 0,27 |
| ∑ | 1 | × | 0,944 |
Ответ: а) 0,944; б) 0,056; в) третий фрилансер.
Условная вероятность. Теорема умножения вероятностей
Пусть А и В – два события, рассматриваемые в данном испытании. При этом наступление одного из событий может влиять на возможность наступления другого. Например, наступление события А может влиять на событие В или наоборот. Для учёта такой зависимости одних событий от других вводится понятие условной вероятности.
Определение. Если вероятность события В находится при условии, что событие А произошло, то получаемая вероятность события В называется условной вероятностью события В. Для обозначения такой условной вероятности используются символы: рА(В) или р(В / А).
Замечание 2. В отличие от условной вероятности, рассматривается и “безусловная” вероятность, когда какие-либо условия наступления некоторого события В отсутствуют.
Пример. В урне 5 шаров, среди которых 3 красных и 2 синих. Поочерёдно из неё извлекают по одному шару с возвратом и без возврата. Найти условную вероятность извлечения во второй раз красного шара при условии, что в первый раз извлечён: а) красный шар; б) синий шар.
Пусть событие А – извлечение красного шара в первый раз, а событие В – извлечение красного шара во второй раз. Очевидно, что р(А) = 3 / 5; тогда в случае, когда вынутый 1-й раз шар возвращается в урну, р(В)=3/5. В случае же когда вынутый шар не возвращается, вероятность извлечения красного шара р(В) зависит от того, какой шар был извлечён в первый раз – красный (событие А) или синий (событие 

Теорема умножения вероятностей событий, одно из которых совершается при условии совершения другого
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло:
Доказательство. Действительно, пусть n – общее число равновозможных и несовместных (элементарных) исходов испытания. И пусть n1 – число исходов, благоприятствующих событию А, которое наступает вначале, а m – число исходов, в которых наступает событие В в предположении, что событие А наступило. Таким образом, m – это число исходов, благоприятствующих событию В. Тогда получим:
р(А ∙ В) = 




Если события А и В поменять ролями в отношении первичного и вторичного совершения, то получим:
Таким образом, в общем случае будем иметь:
Теорема умножения (формула (1.7)) для произвольного числа событий обобщается и имеет вид:
Т.е. вероятность произведения нескольких событий равна произведению вероятности одного из этих событий на условные вероятности других, причём условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.
Пример. В команде из 10 спортсменов 4 мастера спорта. По жеребьёвке из команды выбирают 3-х спортсменов. Какова вероятность того, что все выбранные спортсмены – мастера спорта?
Решение. Приведём задачу к “урновой” модели, т.е. будем считать, что в урне, содержащей 10 шаров, имеется 4 красных шара и 6 белых. Из этой урны наудачу извлекаются 3 шара ( выборка S = 3 ). Пусть событие А состоит в извлечении 3-х шаров. Задачу можно решить двумя способами: по классической схеме и по формуле (1.9).
Первый способ, основанный на формуле комбинаторики:
Второй способ (по формуле (1.9)). Из урны последовательно без возвращения извлекаются 3 шара. Пусть А1 – первый извлечённый шар красный, А2 – второй извлечённый шар красный, А3 – третий извлечённый шар красный. Пусть также событие А означает, что все 3 извлечённых шара – красные. Тогда: А = А1 ∙ (А2 / А1) ∙ А3 / (А1 ∙ А2), т.е.
Пример. Пусть из совокупности карточек а, а, р, б, о, т последовательно извлекаются карточки по одной. Какова вероятность получения слова “работа” при последовательном складывании их в одну строку слева направо?
Пусть В – событие, при котором получается заявленное слово. Тогда по формуле (1.9) получим:
р( В ) = 1/6 ∙ 2/5 ∙ 1/4 ∙ 1/3 ∙ 1/2 ∙ 1/1 = 1/360.
Теорема умножения вероятностей приобретает наиболее простой вид, когда произведение образуется независимыми друг от друга событиями.
Определение. Событие В называется независимым от события А, если его вероятность не меняется от того, произошло событие А или нет. Два события называются независимыми ( зависимыми ), если появление одного из них не изменяет (изменяет) вероятность появления другого. Таким образом, для независимых событий р(В/A) = р(В) или 


Утверждение. Если событие В не зависит от А, то и событие А не зависит от В.
Действительно, если по условию событие В не зависит от А, то р(В/A) = р(В). Запишем теорему умножения вероятностей (1.8) в двух формах:
Заменяя р(В/A) на р(В), получим р(А) ∙ р(В) = р(В) ∙ р(А/B), откуда, предполагая р(В) 
Таким образом, независимость и зависимость событий всегда взаимны. Поэтому справедливо следующее определение независимости (зависимости) событий.