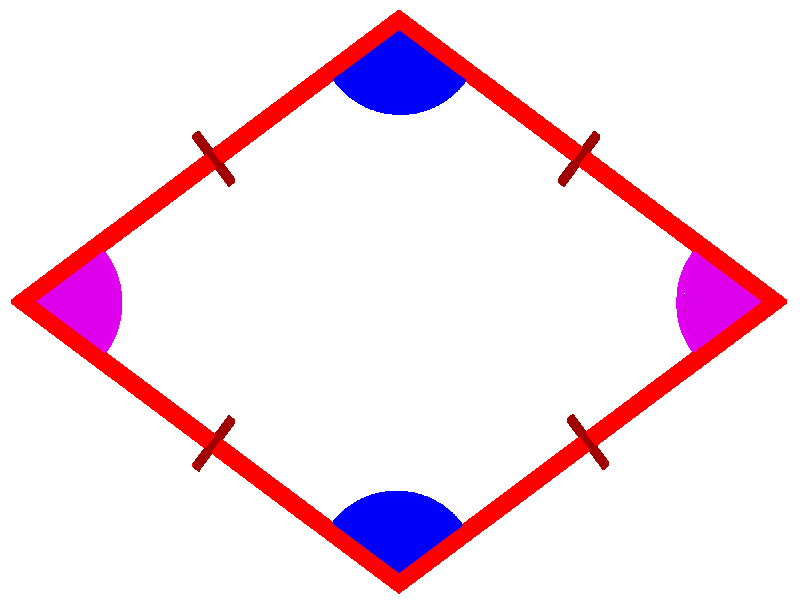
верно ли утверждение что любой квадрат ромб
Любой квадрат является прямоугольником верно или нет
Здравствуйте!
Есть утверждения:
Любой квадрат является прямоугольником.
Можно найти квадрат, который не будет ромбом.
Любой квадрат является ромбом.
Какие верные, а какие нет? Помогите, пожалуйста!
Спасибо!
Утверждение №1.
Любой квадрат является прямоугольником.
Ответ.
Утверждение является совершенно верным.
Чтобы разобраться в правильности этого утверждения достаточно вспомнить определение квадрата. Согласно определению квадратом называют прямоугольник со всеми одинаковыми по длине сторонами. То есть по определению любой квадрат уже прямоугольник.
Утверждение №2.
Можно найти квадрат, который не будет ромбом.
Ответ.
Утверждение является неверным.
Рассмотрим свойства ромба.
Ромбом называется фигура, у которой все стороны равны, противолежащие углы равны, обе диагонали пересекаются под прямым углом. Все эти свойства присущи и квадрату, поэтому утверждение неверно.
А вот обратное утверждение, что можно найти ромб, который не будет квадратом, будет совершенно правильным, так как у ромба не все углы должны быть равны по 90 градусов, как обязательно для квадрата.
Утверждение №3.
Любой квадрат является ромбом.
Ответ.
Утверждение является совершенно верным.
Для определения правильности или неправильности данного утверждения достаточно прочесть объяснение для предыдущего утверждения.
Можно добавить, что квадрат является частным случаем ромба.
Верно ли утверждение что любой квадрат ромб
Укажите номера верных утверждений.
1) Любой квадрат является ромбом.
2) Против равных сторон треугольника лежат равные углы.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Проверим каждое из утверждений.
1) «Любой квадрат является ромбом» — верно, т. к. квадрат — частный случай ромба.
2) «Против равных сторон треугольника лежат равные углы» — верно, т. к. у всякого равнобедренного треугольника при основании равные углы.
3) «Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности» — верно по свойству окружности.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
Проверим каждое из утверждений.
1) «Против большей стороны треугольника лежит меньший угол» — неверно, против большей стороны треугольника лежит больший угол.
2) «Любой квадрат можно вписать в окружность» — верно, по свойству квадрата.
3) «Площадь трапеции равна произведению средней линии на высоту» — верно, по свойству трапеции.
Какие из следующих утверждений верны?
1. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2. В тупоугольном треугольнике все углы тупые.
3. Любой квадрат является прямоугольником.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Рассмотрим каждое из утверждений:
Какие из следующих утверждений верны?
1. Две прямые, перпендикулярные третьей прямой, перпендикулярны.
2. Всякий равносторонний треугольник является остроугольным.
3. Любой квадрат является прямоугольником.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Рассмотрим каждое из утверждений:
1. Две прямые, перпендикулярные третьей прямой, перпендикулярны — неверно, они параллельны.
2. Всякий равносторонний треугольник является остроугольным — верно, в равностороннем треугольнике углы по 60 градусов, следовательно, он остроугольный.
3. Любой квадрат является прямоугольником — верно, т. к. квадрат удовлетворяет всем признакам прямоугольника.
Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.» — неверно, квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
2) «Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.» — верно, по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
3) «Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.» — верно, остроугольным называется треугольник у которого все углы меньше 90°.
4) «В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.» — верно, по теореме Пифагора.
Какие из следующих утверждений верны?
1) Любые два прямоугольных треугольника подобны.
2) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
3) Стороны треугольника пропорциональны косинусам противолежащих углов.
4) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Любые два прямоугольных треугольника подобны.» — неверно, так как нет второго равного угла.
2) «Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.» — верно, по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
3) «Стороны треугольника пропорциональны косинусам противолежащих углов.» — неверно, по теореме синусов стороны треугольника пропорциональны синусам противолежащих сторон.
4) «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.» — верно, по теореме косинусов.
Какие из следующих утверждений верны?
1) Около любого правильного многоугольника можно описать не более одной окружности.
2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.
3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.
4) Около любого ромба можно описать окружность.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Около любого правильного многоугольника можно описать не более одной окружности.»— верно, около любого правильного многоугольника можно описать окружность, и притом только одну.
2) «Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.» — верно, треугольник с такими сторонами является прямоугольным, таким образом, центр окружности лежит на гипотенузе.
3) «Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.» — верно, диагонали квадрата точкой пересечения делятся пополам, таким образом, центром окружности является точка пресечения диагоналей.
4) «Около любого ромба можно описать окружность.» — неверно, чтобы около четырёхугольника можно было описать окружность, необходимо, чтобы сумма противоположных углов четырёхугольника составляла 180°. Это верно не для любого ромба.
Вспоминаем геометрию: ромб и квадрат – в чем отличие? (4 фото)
Что представляет собой ромб
Что представляет собой квадрат
Основные свойства квадрата следующие:
1. Если провести биссектрисы всех углов квадрата (напомним, что углы прямые), то отрезки диагоналей квадрата будут лежать на этих биссектрисах.
2. Если провести диагонали между противоположными углами квадрата, то в центре симметрии квадрата, где эти диагонали пересекутся, они поделятся пополам.
3. Все отрезки диагоналей квадрата будут равны между собой.
Так в чем же отличие?
Проще всего это понять и продемонстрировать ребенку с помощью спичек или зубочисток. Возьмите 4 спички и сделайте из них ромб. Обратите внимание на то, что у ромба разные углы: 2 острых и 2 тупых. А теперь превратите ромб в квадрат – просто сдвиньте спички таким образом, чтобы все углы стали прямыми, то есть по 90º.
Таким образом, получается, что квадрат – это как бы частный случай ромба (хотя настоящему специалисту это определение может показаться не совсем научным).
Еще одно отличие заключается в том, что у квадрата диагонали равны друг другу, а у ромба одна длиннее, а другая короче.
Вывод: каждый квадрат – это ромб с прямыми углами, но не каждый ромб – это квадрат.
Верно ли утверждение что любой квадрат ромб
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны» — верно по признаку подобия треугольников.
2) «Вертикальные углы равны» — верно, это теорема планиметрии.
3) «Любая биссектриса равнобедренного треугольника является его медианой» — неверно, это утверждение справедливо только для равностороннего треугольника.
Заметим, что признак подобия треугольников в учебнике геометрии сформулирован так: «если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны». В утверждении номер 1 опущено слово «соответственно», что не меняет сути.
Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Существует квадрат, который не является прямоугольником» — некорректное утверждение, корректное — «Существует прямоугольник, который не является квадратом».
2) «Если два угла треугольника равны, то равны и противолежащие им стороны» — верно, т. к. треугольник, два угла которого равны является равнобедренным, причём равные стороны лежат напротив равных углов.
3) «Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны» — верно, это теорема планиметрии.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части» — верно по свойству равнобедренного треугольника.
2) «В любом прямоугольнике диагонали взаимно перпендикулярны» — неверно, это утверждение справедливо только для прямоугольника, у которого все стороны равны, то есть для квадрата.
3) «Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу» — верно, т. к. окружность — множество точек, находящихся на заданном расстоянии от данной точки.
Параллелограмм: свойства и признаки
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
Как найти площадь параллелограмма:
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.