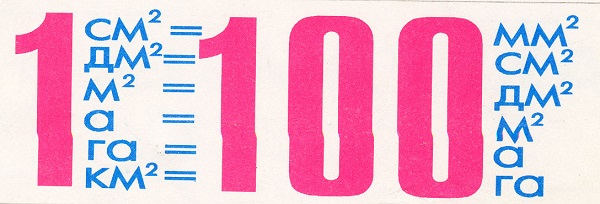величина что это в математике

Величина (математика)

Величина — одно из основных математических понятий, смысл которого с развитием математики подвергался ряду обобщений.

Содержание

История

Ещё в «Началах» Евклида (3 в. до н. э.) были отчётливо сформулированы свойства величины, называемых теперь, для отличия от дальнейших обобщений, положительными скалярными величинами. Это первоначальное понятие величины является непосредственным обобщением более конкретных понятий: длины, площади, объёма, массы и т. п. Каждый конкретный род величины связан с определённым способом сравнения физических тел или др. объектов. Например, в геометрии отрезки сравниваются при помощи наложения, и это сравнение приводит к понятию длины: два отрезка имеют одну и ту же длину, если при наложении они совпадают; если же один отрезок накладывается на часть другого, не покрывая его целиком, то длина первого меньше длины второго. Общеизвестны более сложные приёмы, необходимые для сравнения плоских фигур по площади или пространственных тел по объёму.

Свойства

В более общем смысле слова величинами называют векторы, тензоры и другие «не скалярные величины». Такие величины можно складывать, но отношение неравенства (а 0).

Так как система действительных положительных чисел удовлетворяет перечисленным выше свойствам 1-10, а система всех действительных чисел обладает всеми свойствами скалярных величин, то вполне законно сами действительные числа называть величинами. Это особенно принято при рассмотрении переменных величин. Если какая-либо конкретная величина, например длина l нагреваемого металлического стержня, изменяется во времени, то меняется и измеряющее её число х = l / l_o (при постоянной единице измерения l_o). Само это меняющееся во времени число х принято называть переменной величиной и говорить, что х принимает в какие-либо последовательные моменты времени t₁, t₂,… «числовые значения» X₁, X₂,… В традиционной математической терминологии говорить о «переменных числах» не принято. Однако логичнее такая точка зрения: числа, как и длины, объёмы и т. п., являются частными случаями величины и, как всякие величины, могут быть и переменными, и постоянными. Столь же законно и рассмотрение переменных векторов, тензоров и т. п.

Источник

Измерение величин

Величина — это то, что можно измерить. Такие понятия, как длина, площадь, объём, масса, время, скорость и т. д. называют величинами. Величина является результатом измерения, она определяется числом, выраженным в определённых единицах. Единицы, в которых измеряется величина, называют единицами измерения.

Для обозначения величины пишут число, а рядом название единицы, в которой она измерялась. Например, 5 см, 10 кг, 12 км, 5 мин. Каждая величина имеет бесчисленное множество значений, например длина может быть равна: 1 см, 2 см, 3 см и т. д.

Одна и та же величина может быть выражена в разных единицах, например килограмм, грамм и тонна — это единицы измерения веса. Одна и та же величина в разных единицах выражается разными числами. Например:

Измерить величину — значит узнать, сколько раз в ней содержится другая величина того же рода, принятая за единицу измерения.

Например, мы хотим узнать точную длину какой-нибудь комнаты. Значит нам нужно измерить эту длину при помощи другой длины, которая нам хорошо известна, например при помощи метра. Для этого откладываем метр по длине комнаты столько раз, сколько можно. Если он уложится по длине комнаты ровно 7 раз, то длина её равна 7 метрам.

В результате измерения величины получается или именованное число, например 12 метров, или несколько именованных чисел, например 5 метров 7 сантиметров, совокупность которых называется составным именованным числом.

В каждом государстве правительство установило определённые единицы измерения для различных величин. Точно рассчитанная единица измерения, принятая в качестве образца, называется эталоном или образцовой единицей. Сделаны образцовые единицы метра, килограмма, сантиметра и т. п., по которым изготавливают единицы для обиходного употребления. Единицы, вошедшие в употребление и утверждённые государством, называются мерами.

Меры называются однородными, если они служат для измерения величин одного рода. Так, грамм и килограмм — меры однородные, так как они служат для измерения веса.

Единицы измерения

Ниже представлены единицы измерения различных величин, которые часто встречаются в задачах по математике:

Меры веса/массы:

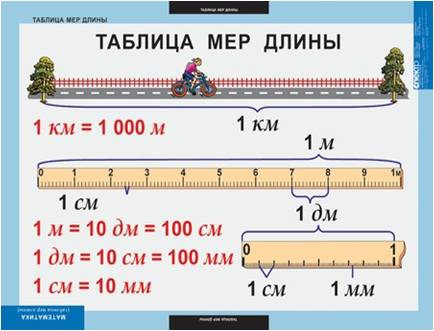
Меры длины:

Меры площади (квадратные меры):

Меры объёма (кубические меры):

Рассмотрим ещё такую величину как литр. Для измерения вместимости сосудов употребляется литр. Литр является объёмом, который равен одному кубическому дециметру (1 литр = 1 куб. дециметру).

Меры времени:

Кроме того, используют такие единицы измерения времени, как квартал и декада.

Месяц принимается за 30 дней, если не требуется определить число и название месяца. Январь, март, май, июль, август, октябрь и декабрь — 31 день. Февраль в простом году — 28 дней, февраль в високосном году — 29 дней. Апрель, июнь, сентябрь, ноябрь — 30 дней.

Год представляет собой (приблизительно) то время, в течении которого Земля совершает полный оборот вокруг Солнца. Принято считать каждые три последовательных года по 365 дней, а следующий за ними четвёртый — в 366 дней. Год, содержащий в себе 366 дней, называется високосным, а годы, содержащие по 365 дней — простыми. К четвёртому году добавляют один лишний день по следующей причине. Время обращения Земли вокруг Солнца содержит в себе не ровно 365 суток, а 365 суток и 6 часов (приблизительно). Таким образом, простой год короче истинного года на 6 часов, а 4 простых года короче 4 истинных годов на 24 часа, т. е. на одни сутки. Поэтому к каждому четвёртому году добавляют одни сутки (29 февраля).

Об остальных видах величин вы узнаете по мере дальнейшего изучения различных наук.

Сокращённые наименования мер

Сокращённые наименования мер принято записывать без точки:

Измерительные приборы

Для измерения различных величин используются специальные измерительные приборы. Одни из них очень просты и предназначены для простых измерений. К таким приборам можно отнести измерительную линейку, рулетку, измерительный цилиндр и др. Другие измерительные приборы более сложные. К таким приборам можно отнести секундомеры, термометры, электронные весы и др.

Измерительные приборы, как правило, имеют измерительную шкалу (или кратко шкалу). Это значит, что на приборе нанесены штриховые деления, и рядом с каждым штриховым делением написано соответствующее значение величины. Расстояние между двумя штрихами, возле которых написано значение величины, может быть дополнительно разделено ещё на несколько более малых делений, эти деления чаще всего не обозначены числами.

Определить, какому значению величины соответствует каждое самое малое деление, не трудно. Так, например, на рисунке ниже изображена измерительная линейка:

Цифрами 1, 2, 3, 4 и т. д. обозначены расстояния между штрихами, которые разделены на 10 одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует 1 мм. Эта величина называется ценой деления шкалы измерительного прибора.

Перед тем как приступить к измерению величины, следует определить цену деления шкалы используемого прибора.

Для того чтобы определить цену деления, необходимо:

В качестве примера определим цену деления шкалы термометра, изображённого на рисунке слева.

Возьмём два штриха, около которых нанесены числовые значения измеряемой величины (температуры).

Например, штрихи с обозначениями 20 °С и 30 °С. Расстояние между этими штрихами разделено на 10 делений. Таким образом, цена каждого деления будет равна:

Следовательно, термометр показывает 47 °С.

Измерять различные величины в повседневной жизни приходится постоянно каждому из нас. Например, чтобы прийти вовремя в школу или на работу, приходится измерять время, которое будет потрачено на дорогу. Метеорологи для предсказания погоды измеряют температуру, атмосферное давление, скорость ветра и т. д.

Источник

Глава 6. Ознакомление детей с величиной(размером) предметов. Обучение измерению

§ 1. Понятие о величине (размере) предметов

Понятие величина в математике рассматривается как основное. Возникло оно в глубокой древности и на протяжении истории развития общества подвергалось ряду обобщений и конкретизации. Величина — это и протяженность, и объем, и скорость, и масса, и число и т. д. В данном же случае мы сужаем понятие «величина» и будем характеризовать им только размер предметов.

Различают два понятия: «прерывная величина» и «непрерывная величина».

Прерывная величина — множество, т. е. величина, в которой составляющие ее элементы строго фиксированы, могут быть отделены друг от друга. Такая величина определяется в основном посредством счета (с помощью чисел или без них).

Непрерывная величина определяется на основе измерения. В этой величине составляющие ее элементы трудно или невозможно отделить друг от друга и пересчитать (сыпучие, жидкие вещества, протяженность, объем).

Понятие величины широко применяется не только в математике, но и в физике, биологии, астрономии и других науках. В методике формирования элементарных математических представлений это понятие используется не всегда корректно: считаются синонимами термины «величина» и

«количество», смешивают понятия «величина» и «значение величины» и др. Объясняется это тем, что понятие величины не является чисто математическим. Применение его во многих отраслях науки привело к разночтению, употреблению его в различных смыслах. В методике обучения математике долгое время понятие величины вообще связывали только с понятием «именованное число». Однако и до настоящего времени педагогическая практика сосредоточивает основное внимание на наиболее характерных признаках величины. Это нередко приводит к смешению понятия величины с понятием меры (числа, выражающего величину после выбора некой единицы измерения).

В математике на вопрос: «Что такое величина?» — ответа в виде определения нет. Однако с помощью исходных свойств, характеризующих величины, строится вся теория и практика формирования представлений и понятий о величине.

Источник

Интернет-урок по математике «Величины и их единицы измерения»

Cartoon Character of Book with sign and pencil

В жизни нам часто приходится что-то исследовать — измерять.

Что мы измеряем в современном мире?

Когда хотим сшить карнавальный костюм, нам надо измерить размер, рост человека, отмерить ткань.

В магазине продавцы взвешивают фрукты, овощи, конфеты.

В больнице измеряют температуру тела человека и давление.

Прежде чем построить дом, следует измерить земельный участок, который потребуется для него, количество материалов, измерить само здание….

Приведи свои примеры измерений …

Ты не забыл про «время»? Ведь время тоже можно измерить. Приведи примеры…

Величина — это это свойство предметов или явлений, которые можно измерить.

1. Найди среди этих слов величины : масса, цвет, длина, запах, объем, аппетит, время, температура.

На нашем интернет-уроке мы познакомимся с величинами: длина, масса, площадь и объём. О времени мы говорили здесь Интернет-урок по математике «Время. Единицы измерения времени»

Величина — длина

В каких случаях мы измеряем длину?…. Верно, расстояние между городами, рост человека, длина стола (чтобы купить для него скатерть), ткань, чтобы хватило на пошив одежды и т.д.

Единицу измерения мы выбирает ту, которая лучше всего подходит для измерения данного предмета.

Если ты будешь измерять расстояние между городами для своего путешествия, ты возьмёшь самую большую единицу измерения — километр.

Если ты будешь делать поделку по технологии и тебе надо вырезать из бумаги шаблон, ты будешь использовать единицу измерения — сантиметр.

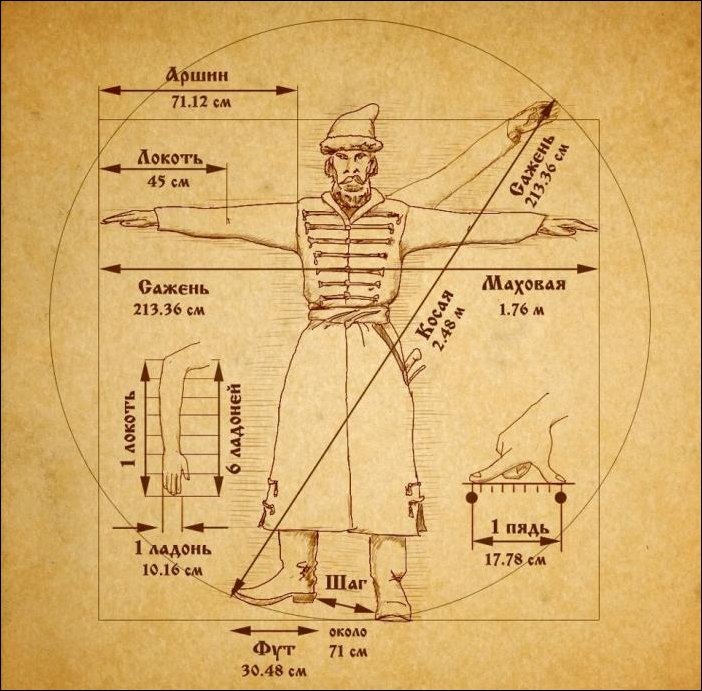
А вот в древности, мерой длины всегда был человек. Система древнерусских мер длины включала в себя следующие основные меры:

Запомни:

Потренируйся:

1. Вырази в сантиметрах:

2. Вырази в дециметрах:

3. Вырази:

5 дм 3 см = … см
7 м = … см
6 м 8 дм = …. см

64 см = … мм
1 дм 5 см = … мм
5 м 82 см = … мм

1 км 4 м = …. м
280 дм = … м
3500 см = … м

4. Реши задачу.

В начале своих занятий в спортивной школе Ваня прыгал в высоту на 1 м 18 см. после нескольких тренировок он стал прыгать на 25 см выше. Какого результата в прыжках в высоту добился Ваня?

Величина — масса

Перед вами две коробки… Чем они отличаются? Нет ответа?

Эти коробки разные по массе! Есть свойства, которые мы не всегда можем увидеть.

Весы — один из древнейших приборов. В Древнем Египте около 5 тысяч лет назад люди уже умели взвешивать.

Сейчас существуют разные весы: в есы для новорожденных детей, аптечные весы, медицинские весы, магазинные весы, бытовые весы, грузовые…

Посмотрим, что изменилось с весами? Почему одна чашечка опустилась, а другая — поднялась? (Одна коробка тяжелее, а другая легче.)

Раньше мерами сыпучих тел были бочка и кадь.
Существовало и много местных мер: короб, рогожа и другие. Позже появились фунт, пуд и другие единицы.
Ещё раньше люди пользовались различными мерками: камнями, яблоками и др. Затем у каждого народа появились свои меры массы. Но все они были неудобны в использовании, так как возникала путаница. Люди долго не могли придумать единую мерку.

В математике принято записывать килограмм КГ

В магазине всегда соль продаётся пачками весом 1 кг!

Величина — площадь

1 км 2 = 1 000 000 м 2

При измерении земельных участков часто ис­пользуются единицы измерения ар и гектар (крат­кая запись а ига).

Величина объём

6. Вырази в заданных единицах длины

4 дм2=…см2
25 дм2=…см2
80 дм2=…см2
1300дм2=…см2
3 дм2 10 см2=..см2
42 дм2 75 см2=…см2
50 дм2 30 см2=…см2
17 дм2 5 см2=..см2

[accordion auto_height=»false» ui_theme=»ui-smoothness»][accordion_panel title=»Проверь себя»] [/accordion_panel] [accordion_panel title=»Ответы»]4 дм2=400см2 25 дм2=2500см2 80 дм2=8000см2 1300дм2=130000см2 3 дм2 10 см2=310см2 42 дм2 75 см2=4275см2 50 дм2 30 см2=5030см2 17 дм2 5 см2=1705см2 [/accordion_panel] [/accordion]

Источник

Понятие величины и её измерения в математике

Длина, площадь, масса, время, объём – величины. Первоначальное знакомство с ними происходит в начальной школе, где величина наряду с числом является ведущим понятием.

1) Любые две величины одного рода сравнимы: они либо равны, либо одна меньше (больше) другой. То есть, для величин одного рода имеют место отношения «равно», «меньше», «больше» и для любых величин и справедливо одно и только одно из отношений: Например, мы говорим, что длина гипотенузы прямоугольного треугольника больше, чем любой катет данного треугольника; масса лимона меньше, чем масса арбуза; длины противоположных сторон прямоугольника равны.

2) Величины одного рода можно складывать, в результате сложения получится величина того же рода. Т.е. для любых двух величин а и b однозначно определяется величина a+b, её называют суммой величин а и b. Например, если a-длина отрезка AB, b – длина отрезка ВС (рис.1), то длина отрезка АС, есть сумма длин отрезков АВ и ВС;

3) Величину умножают на действительное число, получая в результате величину того же рода. Тогда для любой величины а и любого неотрицательного числа x существует единственная величина b= x а, величину b называют произведением величины а на число x. Например, если a – длину отрезка АВ умножить на x= 2, то получим длину нового отрезка АС. (Рис.2)

4) Величины одного рода вычитают, определяя разность величин через сумму: разностью величин а и b называется такая величина с, что а=b+c. Например, если а – длина отрезка АС, b – длина отрезка AB, то длина отрезка ВС есть разность длин отрезков и АС и АВ.

5) Величины одного рода делят, определяя частное через произведение величины на число; частным величин а и b-называется такое неотрицательное действительное число х, что а= х b. Чаще это число – называют отношением величин а и b и записывают в таком виде: a/b = х. Например, отношение длины отрезка АС к длине отрезка АВ равно 2.(Рис №2).

6) Отношение «меньше» для однородных величин транзитивно: если А

Процесс сравнения зависит от рода рассматриваемых величин: для длин он один, для площадей – другой, для масс- третий и так далее. Но каким бы ни был этот процесс, в результате измерения величина получает определённое численное значение при выбранной единице.

Вообще, если дана величина а и выбрана единица величины e, то в результате измерения величины а находят такое действительное число x, что а=x e. Это число x называют численным значением величины а при единице е. Это можно записать так: х=m (a).

Величины, которые вполне определяются одним численным значением, называются скалярными величинами. Такими, к примеру, являются длина, площадь, объём, масса и другие. Кроме скалярных величин, в математике рассматривают ещё векторные величины. Для определения векторной величины необходимо указать не только её численное значение, но и направление. Векторными величинами являются сила, ускорение, напряжённость электрического поля и другие.

В начальной школе рассматриваются только скалярные величины, причём такие, численные значения которых положительны, то есть положительные скалярные величины.

Измерение величин позволяет свести сравнение их к сравнению чисел, операции над величинами к соответствующим операциям над числами.

1. Если величины а и b измерены при помощи единицы величины e, то отношения между величинами a и b будут такими же, как и отношения между их численными значениями, и наоборот.

a=b m (a)=m (b),

a>b m (a)>m (b),

a

Например, если массы двух тел таковы, что а=5 кг, b=3 кг, то можно утверждать, что масса а больше массы b поскольку 5>3.

2. Если величины а и b измерены при помощи единицы величины e, то, чтобы найти численное значение суммы a+b достаточно сложить

численные значения величин а и b. а+b= c m (a+b) = m (a) + m (b). Например, если а = 15 кг, b=12 кг, то а+b=15 кг + 12 кг = (15+12) кг = 27кг

Рассмотренные понятия – объект, предмет, явление, процесс, его величина, численное значение величины, единица величины – надо уметь вычленять в текстах и задачах.

Рассмотрим определения некоторых величин и их измерений.

Источник