векторная и скалярная величина в чем разница
Разница между векторной и скалярной величиной
В физике выделяют 2 категории величин — векторные и скалярные. Что представляют собой те и другие?
Что представляет собой векторная величина?
Под векторной принято понимать величину, имеющую 2 основные характеристики:
Так, два вектора признаются равными, если модули, а также направления обоих совпадают. Записывается рассматриваемая величина чаще всего как буква, над которой прорисовывается стрелка.
В числе самых распространенных величин соответствующего типа — скорость, сила, а также, например, ускорение.
С геометрической точки зрения вектор может представлять собой направленный отрезок, длина которого соотносится с его модулем.
Если рассматривать векторную величину обособленно от направления, то ее принципиально можно измерить. Правда, это будет, так или иначе, частичная характеристика соответствующей величины. Полная — достигается только в случае ее дополнения параметрами направленного отрезка.
Что представляет собой скалярная величина?
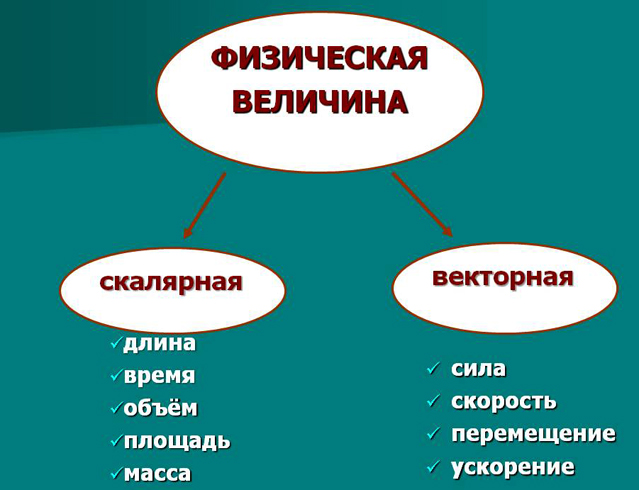
Под скалярной принято понимать величину, которая имеет только 1 характеристику, а именно — численное значение. При этом рассматриваемая величина может принимать положительное или же отрицательное значение.
К распространенным скалярным величинам можно отнести массу, частоту, напряжение, температуру. С ними возможно производить различные математические действия — сложение, вычитание, умножение, деление.
Направление (как характеристика) не свойственно для скалярных величин.
Сравнение
Главное отличие векторной величины от скалярной заключается в том, что у первой ключевые характеристики — модуль и направление, у второй — численное значение. Стоит отметить, что векторную величину, как и скалярную, принципиально можно измерить, правда, в этом случае ее характеристики определятся только частично, поскольку будет недоставать направления.
Определив,в чем разница между векторной и скалярной величиной, отразим выводы в небольшой таблице.
Два вида физических величин: скалярные величины и векторные величины
«Что-то я не помню такой темы в физике» — первое, что, наверное, пришло вам в голову. Да, вы правы — тема незаметная, но в некоторых учебниках она присутствует. «А нужна она мне для ЕГЭ?» Нужна. Точно нужна. Очень нужна. Постоянно нужна.
Давайте приступим. Надо запомнить, что в физике (школьной) есть два типа физических величин:
Векторная величина. Что это такое? Давайте вспомним (а для тех, кто не знал — узнаем), что
Направление вектора изображается на картинке. Куда показывает вектор — туда он и направлен. Например, бывает так, что вектор направлен вверх, вниз и т.д. Вектор может быть направлен вдоль какой-то плоскости. Примеры можете видеть на картинках.
Ну, самое простое — это опыт. Решая задачи, читая теоретический материал, вы со временем запомните, какие величины векторные, а какие скалярные. Физических величин не так много, как может показаться.
А способ чуть посложнее — это представить эти величины и решить для себя: могут они иметь направление? Если да — то это вектор, если нет — скаляр.
Например: заряд конденсатора. Если заряд имеет направление, то куда он направлен? Непонятно — поэтому, скорее всего, заряд — это скалярная величина.
Другой пример: длина отрезка. Если эта физическая величина имеет направление, то откуда куда она направлена: от точки 1 до точки 2? Или от точки 2 до точки 1? Трудно выбрать — поэтому, скорее всего, длина отрезка — это скаляр.
Какие из представленных на рисунках величин являются скалярными, а какие — векторными?
Скаляры и векторы: что это такое
В физике используется много различных математических величин. Например, ускорение, скорость, сила, работа, мощность и так далее. Ученые делят эти величины на два типа: «скалярные» и «векторные». Что же означают эти типы и чем они отличаются?
Скаляр – это величина, которая описывается только значением. Значение этой величины выражает только число. Примеры скалярных величин: скорость, объем, масса, температура, мощность, энергия, время и т.д. Более о скорости читайте в учебнике по физике за 7 класс В.Г. Баряхтяра.
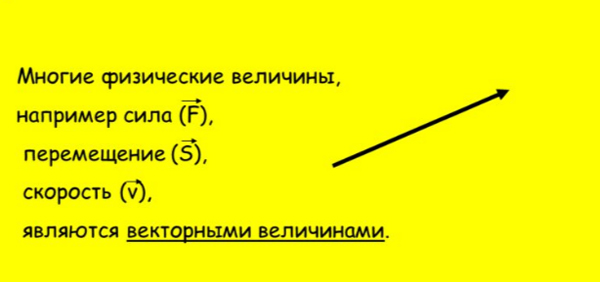
Вектор – это величина, которая имеет как значение, так и направление. Векторные величины важны при изучении движения. Некоторые примеры векторных величин: сила, скорость, ускорение, перемещение и импульс.
Вектор имеет и направление, и значение, а скаляр имеет только значение. Вы можете сказать, является ли величина вектором, просто если поймете, имеет ли эта величина направление.
Как нарисовать вектор?
Вектор нарисован в виде стрелки с головой и хвостом. Величину вектора часто описывают длиной стрелки. Стрелка указывает в направлении вектора.
Векторы обычно пишутся в виде жирных букв. Они также могут быть написаны в виде стрелки над буквой.
Пример вопросов: скаляр или вектор?
1) Футболист бежал со скоростью 15 км в час по направлению к концу зоны.
Это вектор, так как он представляет и значение (15 км/ч) и направление (по направлению к концу зоны).
2) Температура помещения составляет 15 градусов по Цельсию.
Это скаляр, направления нет.
3) Автомобиль разогнался на север со скоростью 4 м/с2 (четыре метра в секунду в квадрате).
Это вектор, поскольку он имеет как направление, так и величину. Мы также знаем, что ускорение – это векторная величина.
Векторная и скалярная величина — чем они отличаются?
В физике существует несколько категорий величин: векторные и скалярные.
Что такое векторная величина?
Векторная величина имеет две основные характеристики: направление и модуль. Два вектора будут одинаковыми, если их значение по модулю и направление совпадают. Для обозначения векторной величины чаще всего используют буквы, над которыми отображается стрелочка. В качестве примера векторной величины можно привести силу, скорость или ускорение.
Для того, чтобы понять сущность векторной величины, следует рассмотреть ее с геометрической точки зрения. Вектор представляет собой отрезок, имеющий направление. Длина такого отрезка соотносится со значением его модуля. Физическим примером векторной величины является смещение материальной точки, перемещающейся в пространстве. Такие параметры, как ускорение этой точки, скорость и действующие на нее силы, электромагнитного поля тоже будут отображаться векторными величинами.
Если рассматривать векторную величину независимо от направления, то такой отрезок можно измерить. Но, полученный результат будет отображать только лишь частичные характеристики величины. Для ее полного измерения следует дополнить величину другими параметрами направленного отрезка.
В векторной алгебре существует понятие нулевого вектора. Под этим понятием подразумевается точка. Что касается направления нулевого вектора, то оно считается неопределенным. Для обозначения нулевого вектора используется арифметический нуль, набранный полужирным шрифтом.
Что такое скалярная величина?
В отличие от вектора, скалярная величина обладает только лишь одним параметром – это ее численное значение. Стоит отметить, что анализируемая величина может иметь как положительное численное значение, так и отрицательное.
В качестве примера можно привести массу, напряжение, частоту или температуру. С такими величинами можно выполнять различные арифметические действия: сложение, деление, вычитание, умножение. Для скалярной величины такая характеристика, как направление, не свойственна.
Скалярная величина измеряется числовым значением, поэтому ее можно отображать на координатной оси. Например, очень часто строят ось пройденного пути, температуры или времени.
Основные отличия между скалярными и векторными величинами
Из описаний, приведенных выше, видно, что главное отличие векторных величин от скалярных заключается в их характеристиках. У векторной величины есть направление и модуль, а у скалярной только численное значение. Безусловно, векторную величину, как и скалярную, можно измерить, но такая характеристика не будет полной, так как отсутствует направление.
Для того, чтобы более четко представить отличие скалярной величины от векторной, следует привести пример. Для этого возьмем такую область знаний, как климатология. Если сказать, что ветер дует со скоростью 8 метров в секунду, то будет введена скалярная величина. Но, если сказать, что северный ветер дует со скоростью 8 метров в секунду, то речь пойдет о векторном значении.
Векторы играют огромную роль в современной математике, а также во многих сферах механики и физики. Большинство физических величин может быть представлено в виде векторов. Это позволяет обобщить и существенно упростить используемые формулы и результаты. Часто векторные значения и векторы отождествляются друг с другом. Например, в физике можно услышать, что скорость или сила является вектором.
Некоторые формулы векторной алгебры используются в таких областях науки, как:
Четкое осознание разницы между векторной и скалярной величиной позволит специалистам решать сложные задачи и более подробно характеризовать используемые данные.
Векторная и скалярная величина в чем разница
В физике существуют скалярные величины (скаляры) и векторные величины (векторы). Хотя, правильнее в последнем случае все-таки говорить векторная величина, часто говорят, например, «вектор скорости».
Чтобы совсем запутаться, рекомендую обратиться к Википедии: https://ru.wikipedia.org/wiki/Векторная_величина.
Для нас важно понять два момента:
1) Примерами скаляров являются: длина, площадь, время, масса, плотность, температура и т.п.
Для наших задач достаточно понимания скаляра, как величины (числа с размерностью) без направления.
2) Под вектором мы будем понимать направленный отрезок. То есть три числа (мы ведь живем в трехмерном пространстве), которые преобразуются по определенным правилам при переходе от одной системы координат к другой.
Попробуем обойтись без математических формул этих правил. Просто представим в нашем трехмерном пространстве направленный отрезок. Некую стрелку, которая, для простоты, неподвижна, неизменна, и имеет направление от одного конца к другому. Или даже представим, что у нас есть определенная операция перемещения в пространстве. У нее есть величина (расстояние перемещения по прямой из начальной точки в конечную) и направление.
И представим систему координат (например, прямоугольную), которая неподвижна относительно нас, и начало отсчета которой совпадает с началом нашего направленного отрезка.
Отлично! Тогда координаты «заостренного» конца нашего «направленного» отрезка с началом в точке (0,0,0) в этой системе координат будут выражаться тремя числами (Ах, Аy, Аz). Будет ли эта тройка чисел вектором?
Теперь мы берем и поворачиваем произвольно нашу систему координат (но пока не сдвигаем начало координат). Тогда в новой системе координат координаты нашего вектора будут (Аx’, Аy’, Аz’). Заметьте, сам наш вектор (направленный отрезок в трехмерном пространстве) не изменился. Как бы мы не вращали систему координат, тройка чисел будет меняться, но вектор (в смысле направленного отрезка) останется на своем месте. Он смотрит в одну и ту же «точку вселенной». О как! И длина его не меняется из-за вращения системы координат.
А теперь вывод. То, что важно для физики!
Формулы можно посмотреть у Фейнмана или еще где-нибудь. Они пока для понимания не столь важны. А важно следующее!
Теперь посмотрим, что есть что.
Путь вектор или скаляр? Скаляр. Почему?
Далее сами перебираем физические величины и определяем, что есть скаляр, а что вектор!