в сопротивлении материалов вводится допущение о сплошности материала что позволяет
Тема 2.1 Основные понятия и допущения
Элементы сооружений отличаются друг от друга формами, размерами, материалом, функциональным назначением, рядом специальных требований. При этом следует отметить, что все без исключения элементы как искусственного, так и естественного происхождения обладают такими свойствами, как прочность и жесткость, то есть способностью, не разрушаясь воспринимать различные нагрузки и сопротивляться изменению своих первоначальных форм и размеров, без чего не может нормально функционировать сооружение. Цель расчетов в сопротивлении материалов – создание прочных, устойчивых, обладающих достаточной жесткостью, долговечностью и вместе с тем экономичных элементов сооружений
Например, конструкции стропильной фермы, междуэтажных перекрытий зданий должны выдерживать нагрузки от атмосферных воздействий, оборудования и людей и обладать достаточной жесткостью, обеспечивающей ограничение прогибов для создания нормальных условий функционирования сооружения.
Рис. 1. Характер деформирования и разрушения стержня под нагрузкой:
а) – элемент до нагружения; б) – деформация стержня при изгибе; в) – вид излома элемента при изгибе; г) – изгиб стержня при сжатии
Прочностные и жесткостные качества элементов сооружений зависят от многих факторов: материала, размеров, характера возникающих деформаций и др. Металлические конструкции обладают большей прочностью и жесткостью, чем аналогичные деревянные конструкции. Стержень из одного и того же материала, имеющий большие поперечные размеры, более прочный и жесткий, при этом его легче разрушить, изгибая, чем растягивая. Тонкий стержень при его сжатии разрушается в результате выпучивания в поперечном направлении, в то же время это явление отсутствует при продольном растяжении и для разрушения стержня требуется значительно большая нагрузка.
Например, возьмем деревянный брусок (рис.1, а). Начнем сгибать стержень. Чем сильнее мы будем прикладывать усилия, тем больше он изогнется (рис.1 б), и при какой то величине усилий сломается (рис.1, в). Подведя итог можно утверждать, что всякое реальное тело под воздействием сил меняет свою форму и размеры, т. е. деформируется. Деформации обуславливают появление внутри элемента сил сопротивления. Если внешние силы больше сил сопротивления, происходит разрушение элемента сооружения.
При возрастании нагрузки выше определенных значений в теле наряду с упругими будут возникать деформации не исчезающие после снятия нагрузки. Такие деформации называются остаточными. Возникновение остаточных деформаций, наравне с разрушением связано с нарушением нормальной работы конструкции и, как правило, недопустимо.
Способность конструкции воспринимать заданную нагрузку, не разрушаясь и без остаточных деформаций, называют прочностью.
Все элементы сооружения, из каких бы материалов они ни были изготовлены, под нагрузкой деформируются. Однако значительные деформации могут мешать нормальной эксплуатации сооружения.
Способность сооружений и ее частей под нагрузкой сохранять свои размеры и форму в установленных нормами пределах называется жесткостью.
Рассмотрим еще один пример. Будем сжимать тонкий и длинный стержень (тот же деревянный брусок). Уже при незначительной силе стержень изогнется, как показано на рис.1, г. В этом случае первоначальная форма прямолинейная форма равновесия стержня становится неустойчивой.
Способность конструкции, и ее частей, сохранять под нагрузкой первоначальную форму упругого равновесия называется устойчивостью. Обычно потеря устойчивости сопровождается мгновенным изменением формы элемента и разрушением конструкции.
Методами сопротивления материалов выполняются расчеты, на основании которых определяются необходимые размеры деталей машин и конструкций инженерных сооружений. Любая конструкция должна обладать надежностью при эксплуатации и быть экономичной.
Надежность – свойство конструкции выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных нормативных пределах в течение требуемого промежутка времени.
В сопротивлении материалов широко применяются методы теоретической механики и математического анализа, используются данные из разделов физики, изучающих свойства различных материалов, материаловедения и других наук. К тому же сопротивление материалов является наукой экспериментально-теоретической, так как она широко использует опытные данные и теоретические исследования.
ЗАДАНИЕ:
Что изучает раздел «Сопротивление материалов»?
Выписать определения: прочность, жесткость, устойчивость, надежность и экономичность.
§2. Реальный объект и расчетная схема
При выборе расчетной схемы вводятся упрощения (схематизация) реального объекта, т.е. отбросить все те факторы, которые не могут сколько-нибудь заметным образом повлиять на работу системы в целом.
Такого рода упрощения задачи совершенно необходимы, так как решение с полным учетом всех свойств реального объекта является принципиально невозможным в силу их очевидной неисчерпаемости.
Основным упрощающим приемом в сопротивлении материалов является приведение геометрической формы тела к схемам бруса (стержня), оболочки или пластины. Как известно, любое тело в пространстве характеризуется тремя измерениями.
Рис. 2. Прямой брус (стержень) постоянного сечения
ЗАДАНИЕ:
У казать чем отличается расчетная схема от реального объекта.
Начертить стержень, изобразив его ось и поперечное сечение, записать определение стержня.
§3. Связи и опорные устройства
Для соединения отдельных частей конструкции между собой и передачи внешней нагрузки на основание на нее накладываются связи , ограничивающие перемещения тех точек сооружения, к которым они приложены. Связи могут ограничивать либо повороты точек сооружения, либо их линейные смещения, либо и то и другое.
Основным видом связей в расчетной схеме является шарнирная связь.
Все опорные связи условно делятся на три основных типа:
— Подвижная шарнирная опора (рис.3, а). Такая опора не препятствует вращению конца бруса и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через ось катка (R).
— Жесткая заделка или защемление (рис.3, в). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре в общем случае может возникать реакция, которую обычно раскладывают на две составляющие (H и R) и момент защемления (М).
При рассмотрении реального объекта в число внешних сил включаются не только заданные нагрузки, но и реакции связей (опор), дополняющие систему сил до равновесного состояния.
§4. Внешние и внутренние силы. Метод сечений
Поверхностные силы приложены к участкам поверхности и являются результатом непосредственного контактного взаимодействия рассматриваемого объекта с окружающими телами (давление ветра, воды на стенку).
В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные нагрузки подразделяются на сосредоточенные и распределенные.
Динамические нагрузки также подразделяются на периодические и случайные нагрузки. К случайным нагрузкам относятся нагрузки, действующие на детали автомобилей, тракторов, станков, а также нагрузки, действующие на сооружения (дома, мачты, краны и т.п.) от давления ветра, снега и т.п.
Временная нагрузка может сохранять более или менее постоянную величину в течение всего периода ее действия, а может непрерывно изменяться по некоторому закону; в последнем случае она называется переменной нагрузкой.
По отношению к выбранному материальному телу (элементу конструкции) все действующие силы подразделяются на внешние и внутренние силы. Под внешними силами (нагрузками) понимаются силы взаимодействия данного материального тела со всеми другими окружающими его телами.
Взаимодействие между частями рассматриваемого тела характеризуется внутренними силами , которые возникают внутри тела под действием внешних нагрузок и определяются силами межмолекулярного воздействия. Эти силы сопротивляются стремлению внешних сил разрушить элемент конструкции, изменить его форму, отделить одну часть от другой. Вообще внутренние силы возникают между всеми смежными частицами тела при нагружении.
ЗАДАНИЕ:
Составить таблицу «Виды нагрузок», в таблице дать характеристику каждому виду нагрузки.
Рис.4. Внутренние силовые факторы, возникающие при действии нагрузки
В зависимости от вида внутренних силовых факторов, возникающих в сечении, различают различные следующие виды нагружения бруса:
— Растяжение или сжатие. Действует только продольная сила N.
— Кручение. Действует только крутящий момент T.
— Сдвиг. Действует только поперечная сила Q x или Q y
— Изгиб. Действует только изгибающий момент M x или M y (чистый изгиб), при действии изгибающего момента и поперечной силы (поперечный изгиб).
— Сложное сопротивление. Одновременное действие нескольких силовых факторов. Например, M x и T, M и N.
Итак, внутренние усилия в сечении есть функции параметров, определяющих положение сечения в теле, и нагрузок по одну сторону от сечения. Эти функции могут быть представлены аналитически или графически. График, показывающий изменение внутреннего усилия в зависимости от положения сечения, называется эпюрой . Ординаты усилий в определенном масштабе откладывают от линии, соответствующей оси бруса.
ЗАДАНИЕ:
Начертить внутренние силовые факторы стержня(рис. 4), дать пояснение каждому символу на этой схеме и указать вид нагружения при котором возникают N , Q y и Q z , Т , M z и М у .
§5. Допущения, применяемые в сопротивлении материалов
Для построения теории сопротивления материалов принимают некоторые понятия и допущения относительно структуры и свойств материалов, а также о характере деформаций. Приведем основные из них.
1. В сопротивлении материалов принято рассматривать все материалы как однородную сплошную среду, независимо от их микроструктуры. Под однородностью материала понимают независимость его свойств от величины выделенного из тела объема. И хотя в действительности реальный материал, как правило, неоднороден (уже в силу его молекулярного строения), тем не менее, указанная особенность не является существенной, поскольку в сопротивлении материалов рассматриваются конструкции, размеры которых существенно превышают не только межатомные расстояния, но и размеры кристаллических зерен.
Металлы и сплавы, как правило, изотропны, так как большинство металлов имеет мелкозернистую структуру. Благодаря большому количеству кристаллов свойства материалов выравниваются в различных направлениях и можно считать эти материалы практически изотропными. В настоящее время широкое распространение получили анизотропные композиционные материалы, состоящие из двух компонентов – наполнителя и связующего. Наполнитель состоит из уложенных в определенном порядке высокопрочных нитей – матрицы, что и определяет значительную анизотропию композита. Композиционные материалы имеют высокую прочность при значительно меньшем, чем металлы весе.
Результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, прилагаемых к телу последовательно и в любом порядке (рис. 6). Под словами «результат воздействия» следует понимать – деформации, внутренние силы и перемещения отдельных точек.
Допущения и гипотезы сопротивления материалов
В сопротивлении материалов, как в инженерной прикладной науке, приходится рассматривать идеализированное тело, отступая в допустимых пределах от реальных условий, отвлекаясь от несущественных связей и сторон изучаемого явления, схематизируя сложные явления и выделяя для материалов ряд присущих им в той или иной степени основных общих свойств. Это достигается принятием в сопротивлении материалов некоторых допущений и гипотез, при помощи которых реальное тело упрощается, т.е. подменяется идеальным, но сохраняющим в то же время его основные практические свойства реального и лишенным его второстепенных свойств.
К основным допущениям сопротивления материалов относятся:
1) абсолютной упругости тела в определенных пределах, т.е. способности восстанавливать свои размеры и форму после прекращения действия нагрузки;
2) сплошности тела без пустот, когда допускается, что однородная его масса заполняет объем тела полностью и пренебрегается молекулярной структурой материала; это допущение подтверждается экспериментально сопоставлением опытных данных испытаний тел с расчетами методами сопротивления материалов;
3) однородности, т.е. одинаковости свойств материала тела в каком-либо одном направлении;
4) изотропности, т.е. одинаковости свойств тела во всех направлениях в окрестности любой точки материала; свойствами однородности и изотропности обладают большинство конструкционных материалов.
Кроме допущений в сопротивлении материалов применяются также гипотезы, существенно упрощающих расчеты, к которым относятся:
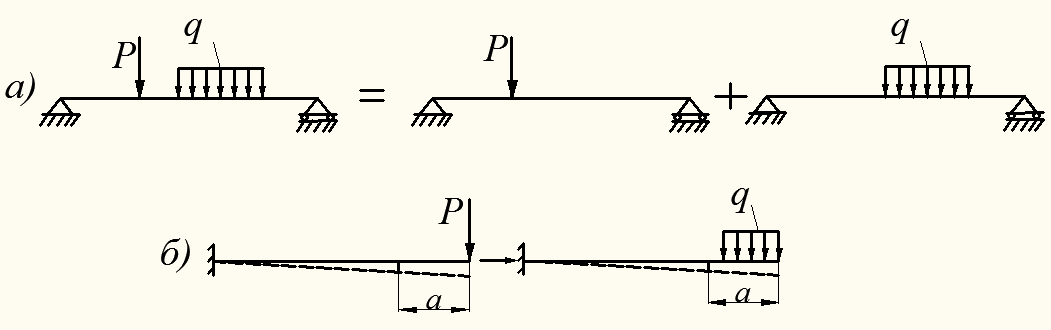
1) принцип независимости действия сил (принцип суперпозиции), согласно которому результат воздействия на тело нескольких сил равен сумме действия каждой из сил в отдельности (рис. 1.3, а):
2) принцип Сен-Венана: вдали от места приложения нагрузки на расстоянии а результат мало зависит от вида нагрузки; например (рис. 1.3, б), заменяя распределенную нагрузку интенсивностью q, приложенную на небольшом участке, на сосредоточенную силу Р, равную равнодействующей распределенной нагрузки.
Рисунок 1.3 – Примеры использования гипотез в сопротивлении материалов
3) гипотеза плоских сечений: сечения бруса, перпендикулярные к его оси до нагружения, остаются плоскими и перпендикулярными к этой оси после нагружения.
Перечисленные допущения и гипотезы, конечно, приводят к тому, что расчеты, предлагаемые теорией сопротивления материалов, являются приближенными. Однако опытная проверка расчетов, полученных на основании этой приближенной теории, подтверждает достаточную их точность для практического использования.
Дата добавления: 2016-10-18 ; просмотров: 4514 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Тестовые задания по сопротивлению материалов.
Депобразования и молодежи Югры
бюджетное учреждение профессионального образования
Ханты-Мансийского автономного округа – Югры
«Мегионский политехнический колледж»
(БУ «Мегионский политехнический колледж»)
Тестовые задания по сопротивлению материалов.
Преподаватель физики и технической механики
Методические указания для студентов очной и заочной форм обучения.
Направление: Специальность 131018 Разработка и эксплуатация нефтяных и газовых месторождений.
2.3. Механические свойства материалов 17
1.1. Основные понятия, определения, допущения и принципы
Задание 1.1.1: Утверждение, что напряжения и перемещения в сечениях, удаленных от места приложения внешних сил, не зависят от способа приложения нагрузки, называется…
1) принципом независимости действия сил;
2) гипотезой плоских сечений;
3) принципом начальных размеров; 4) принципом Сен-Венана.
Задание 1.1.2: Сопротивление материалов – это наука о методах расчета элементов инженерных конструкций на…
1) жесткость; 2) прочность; 3) устойчивость;
4) прочность, жесткость и устойчивость.
Решение: Верный ответ – 4). В процессе эксплуатации материал инженерных конструкций не должен разрушаться; перемещения отдельных точек конструкции не должны превосходить определенных, наперед заданных величин; форма конструкции не должна существенно изменяться. Если эти требования не выполняются, конструкция перестает нормально функционировать.
Задание 1.1.3: Способность конструкции, элементов конструкции сопротивляться внешним нагрузкам в отношении изменения формы и размеров называется…
1) упругостью; 2) устойчивостью; 3) твердостью; 4) жесткостью.
Решение: Верный ответ – 4). Твердые тела в той или иной мере способны до определенного предела воспринимать воздействие внешних сил без разрушения и без существенного изменения первоначальных геометрических размеров.
Задание 1.1.4: Свойство материала тела восстанавливать свои первоначальные размеры после снятия внешних сил называется…
Варианты ответов:
1) твердостью; 2) однородностью; 3) упругостью; 4) изотропностью.
Решение: Верный ответ – 3). Под действием внешних сил реальное тело меняет геометрические размеры. После снятия внешних сил размеры тела полностью или частично восстанавливаются.
Задание 1.1.5: В соответствии с принципом независимости действия сил (принцип суперпозиции) …
1) механические характеристики материала в окрестности заданной точки не зависят от угловой ориентации выделенного из тела образца;
2) результат действия системы сил равен сумме результатов действий каждой силы в отдельности;
3) при снятии нагрузки форма и размеры тела полностью восстанавливаются;
4) большинство расчетов в сопротивлении материалов производится по недеформированной схеме.
Задание 1.1.6: Механическое свойство, характеризующее способность материала сопротивляться его разрушению под действием внешних сил, называется…
1) твердостью; 2) упругостью; 3) изотропностью; 4) прочностью.
1.2. Модели прочностной надежности
Задание 1.2.1: Если свойства материала образца, выделенного из тела, не зависят от его угловой ориентации, то такой материал называется…
1) однородным; 2) изотропным; 3) идеально – упругим;
Решение: Верный ответ – 2). Элементы конструкций изготавливаются из различных материалов. Их структура и физические свойства могут быть весьма разнообразны. Например, металлы имеют поликристаллическую структуру и состоят из множества кристаллов расположенных в объеме тела случайным образом. Отдельно взятый кристалл металла анизотропен. Но если в объеме содержатся весьма большое количество хаотически ориентированных кристаллов, то материал можно рассматривать как изотропный, т.е. предполагать, что свойства материала тела, выделенного из данного объема, во всех направлениях одинаковы.
Задание 1.2.2: В сопротивлении материалов относительно структуры и свойств материала принимаются гипотезы…
1) устойчивости и жесткости;
2) сплошности, однородности, изотропности и идеальной упругости материала;
3) изотропности и идеальной упругости;
4) сплошности и однородности материала.
Решение: Верный ответ – 2). Строго говоря, любой материал нельзя рассматривать как сплошную, однородную среду. Отдельно взятый кристалл металла анизотропен. Все реальные тела обнаруживают отступление от свойств идеальной упругости. Решение задач с учетом всех свойств реального материала невозможно в силу их очевидной неисчерпаемости.
Гипотезы сплошности, однородности, изотропности и идеальной упругости позволяют упростить задачи, решаемые в курсе «Сопротивления материалов», и довести их до числового результата.
Задание 1.2.3: Разделение тела на части под действием внешних нагрузок называется…
1) разрушением; 2) пластичностью; 3) прочностью;
4) идеальной упругостью.
Задание 1.2.4: Объект, освобожденный от особенностей, несущественных при решении данной задачи, называется…
1) реальной конструкцией; 2) расчетной схемой;
3) абсолютно твердым телом; 4) математической моделью.
Задание 1.2.5: Положение, согласно которому материал полностью заполняет весь объем тела, называется …
1) гипотезой изотропности; 2) гипотезой сплошности;
3) гипотезой однородности; 4) принципом Сен-Венана.
Задание 1.2.6: Тело, один размер которого намного превышает два других, называется…
1) стержнем; 2) массивом; 3) пластиной; 4) оболочкой.
1.3. Внутренние силы и напряжения
Задание 1.3.1: Векторная величина, которая характеризует интенсивность распределения внутренних сил по сечению тела, называется…
1) касательным напряжением; 2) напряженным состоянием в точке;
3) полным напряжением в точке; 4) нормальным напряжением.
Векторная величина р называется полным напряжением в точке.
Задание 1.3.2: Полное напряжение в точке сечения, в общем случае, раскладывается на…
1) нормальное напряжение; 2) среднее напряжение;
3) касательное напряжение; 4) нормальное и касательное напряжения.
Решение: Верный ответ – 4). Полное напряжение в точке сечения, в общем случае, раскладывается на нормальное и касательное напряжения.
Задание 1.3.3: Для определения внутренних силовых факторов, действующих в сечении тела, используется…
1) метод сил; 2) принцип независимости действия сил;
3) гипотеза плоских сечений; 4) метод сечений.
Задание 1.3.4: Проекции главного вектора и главного момента всех внутренних сил в данном сечении на три взаимно перпендикулярные оси, расположенные в этом же сечении по определенному правилу, называются…
1) поперечными силами и изгибающими моментами;
2) сосредоточенными силами и моментами;
3) компонентами напряженного состояния;
4) внутренними силовыми факторами.
Задание 1.3.5: В системе СИ напряжение измеряется в …
Задание 1.3.6: Силы взаимодействия между частями рассматриваемого тела называются…
1) внешними; 2) объемными; 3) внутренними; 4) поверхностными.
1.4. Перемещения и деформации
Задание 1.4.1: Упрощение, на основании которого при составлении уравнений равновесия тело, после нагружения внешними силами рассматривают как недеформированное, называется…
1) принципом независимости действия сил;
2) принципом начальных размеров;
3) условием неразрывности деформаций; 4) твердостью.
Решение: Верный ответ – 2). Все твердые тела под действием внешних сил деформируются, то есть меняют свои размеры. Для подавляющего большинства тел перемещения точек являются малыми по сравнению с геометрическими размерами тела. На основании малости перемещений в методику анализа внутренних сил в теле вводят следующее упрощение. При составлении уравнений равновесия тело рассматривают как недеформированное, имеющее те же геометрические размеры, какие оно имело до нагружения.
1) абсолютным удлинением; 2) средним удлинением; 3) напряжением;
4) абсолютным укорочением в направлении оси x ;
Задание 1.4.3: Угловым перемещением сечения является величина…
Задание 1.4.4: Количественная мера изменения геометрических размеров в окрестности точки называется…
1) полным перемещением точки; 2) абсолютным удлинением стержня;
3) линейной деформацией; 4) деформированным состоянием в точке.
1) полным перемещением; 2) угловой деформацией;
3) проекцией вектора перемещения; 4) линейной деформацией.
Растяжение и сжатие
2.1. Продольная сила. Напряжения и деформации
Задание 2.1.1: Для стержня, схема которого изображена на рисунке, продольная сила N в сечении 2-2 будет…
1) равной нулю; 2) равномерно распределенной по сечению;
3) растягивающей; 4) сжимающей.
Решение: Верный ответ – 2). Для определения продольной силы следует рассмотреть равновесие отсеченной правой части стержня 
, откуда 
.
Задание 2.1.2: Сплошной однородный стержень круглого поперечного сечения диаметром d нагружен так, как показано на рисунке. Нормальные напряжения в сечении 1-1 равны…
Решение: Верный ответ – 2). Нормальные напряжения при растяжении − сжатии определяются по формуле 
. Продольная сила N определяется из условия равновесия для отсеченной части стержня
; 
. Откуда N =0. В результате 
. 
Задание 2.1.3: Из гипотезы плоских сечений следует, что вдали от мест нагружения, резкого изменения формы и размеров поперечного сечения нормальные напряжения при растяжении − сжатии прямолинейных стержней распределяются по площади поперечного сечения …
1) по закону квадратной параболы, достигая максимума на нейтральной линии;
2) по линейному закону, достигая минимума на нейтральной линии;
3) неравномерно, в зависимости от формы поперечного сечения;
Задание 2.1.4: Распределение нормальных напряжений при растяжении − сжатии вдали от мест нагружения, резкого изменения формы и размеров поперечного сечения существенно зависит от…
1) величины и способа приложения внешних сил;
2) величины приложенных внешних сил;
3) способа приложения внешних сил;
4) от формы поперечного сечения
Задание 2.1.5: Для стержня круглого поперечного сечения, схема которого изображена на рисунке, абсолютное удлинение ∆ L равно…
1) 
; 2) 
; 3) 
; 4) 0
Удлинение стержня 
.
В нашем случае , 
, 
. Площадь сечения 
. Окончательно 
.
1) 
; 2) 
; 3) 
; 4) 
.
Уравнение равновесия имеет вид: 
. Откуда 
. Далее определяем нормальное напряжение: 
. Из закона Гука 
вычислим значение продольной деформации:
.
Второй способ определения величины 
. Сначала определяем абсолютное удлинение участка СК : 
, а затем продольную линейную деформацию на этом участке: 
.
2.2. Испытание конструкционных материалов на растяжение и сжатие
Задание 2.2.1: При испытании на растяжение нормального образца (диаметр d 0 = 10мм, длина расчетной части до разрыва l 0 = 100мм) относительное остаточное удлинение составило = 25%. Длина расчетной части образца после разрыва составляет…
1) 50 мм; 2) 25 мм; 3) 100,25 мм; 4) 125 мм.
Решение: Верный ответ – 4). Относительное остаточное удлинение при разрыве равно 
. Отсюда находим искомую длину расчетной части 
мм.
Задание 2.2.2: Для образца из некоторого материала получили диаграмму растяжения и определили все основные механические характеристики. Деталь из этого материала будет работать при статической нагрузке как на растяжение, так и на сжатие. В этом случае…
1) необходимо провести испытания на сдвиг и сжатие;
2) необходимо провести испытания на сжатие;
3) необходимо провести испытания на кручение;
4) дополнительные испытания не требуются.
Задание 2.2.3: Образец из хрупкого материала испытали на сжатие. Вид образца после испытания (сплошная линия) изображен на рисунке…
1) 
2) 
3) 
4) 
Задание 2.2.4: Диаграммой растяжения образца является диаграмма…
1) 
2) 
3) 
4) 
Задание 2.2.5: Материал является хрупким, если образец из него …
1) разрушается при достаточно небольшой нагрузке;
2) разрушается только при достаточно большой нагрузке;
3) разрушается при очень малых остаточных деформациях (до 5%);
4) разрушается при больших остаточных деформациях (свыше 5%).
Задание 2.2.6: Стальной образец, предназначенный для испытания на растяжение при статическом нагружении, имеет вид …
1) 
; 2) 
3) 
; 4) 
.
2.3. Механические свойства материалов
1) 255 МПа ; 2) 510 МПа; 3) 155 МПа; 4) 125 МПа;
Решение: Верный ответ – 3). Допускаемое напряжение материала 
. В качестве предельного напряжения пред принимается:
— для пластичных материалов предел текучести т ;
— для хрупких материалов предел прочности ппр .
Задание 2.3.2: На представленной диаграмме зависимости напряжения от деформации для конструкционной стали точка D соответствует пределу…
1) упругости; 2) прочности; 3) текучести; 4) пропорциональности.
1) предела прочности 
при разрыве;
2) относительного остаточного удлинения при разрыве 
;
3) удлинения стержня 
при разрыве;
4) предела пропорциональности 
при разрыве.
Задание 2.3.4: Коэффициентом Пуассона называется…
1) отношение максимальной силы, которую способен выдержать образец, к начальной площади его поперечного сечения;
2) отношение нормального напряжения к величине относительной деформации в законе Гука;
3) отношение относительной поперечной деформации к относительной продольной деформации, взятое по абсолютной величине;
4) остаточное сужение при разрыве 
, где А 0 и А 1 – начальная и конечная площади поперечного сечения образца
Задача 2.3.5: Наклеп (нагартовка) – это…
1) изменения напряжений и деформаций в нагруженной детали;
2) соединение материала клепками или заклепками;
3) повышение упругих свойств материала в результате предварительного пластического деформирования;
4) уменьшение удлинения при разрыве и незначительное возрастание предела прочности при длительном пребывании в нагретом состоянии.
1) 408; 2) 611; 3) 306; 4) 153.
МПа.
2.4. Расчеты стержней на прочность и жесткость
Задание 2.4.1: Допускаемое напряжение [σ] = 160 МПа. Диаметры круглых поперечных сечений стержней d 1 и d 2 в мм будут равны …
1) 18,08 и 19,37; 2) 10,17 и 10,93; 3) 11,74 и 16,60; 4) 20,4 и 21,85.
Из уравнений проекций всех сил на оси у, х получим:
Диаметры стрежней определяются из условий прочности: 
. Площади поперечных сечений 
.
Тогда 
м=20,4мм;
м=21,85мм.
1) 288 МПа; 2) 219,5 МПа; 3) 320 кН; 4) 256 кН.
Допустимая нагрузка 
.
1) 22,36 см; 2) 22 см; 3) 5 см; 4) 10 см.
По условию жесткости 
.
Отсюда 
Задание 2.4.4: Допускаемое напряжение на растяжение − сжатие для материала стержня равно 150 МПа. Для стержня круглого поперечного сечения наименьший размер D из условия прочности равен…
1) 10 см; 2) 8,9 см; 3) 8,34 см; 4) 13.
.
Задание 2.4.5: К стержню квадратного поперечного сечения приложены одинаковые растягивающие силы. Если одновременно увеличить в 2 раза длину стержня и размер стороны, абсолютное удлинение стержня…
1) увеличится на 0,25 l ; 2) уменьшится в 2 раза;
Задание 2.4.6: Прямой стержень изготовлен из хрупкого материала и нагружен осевыми силами. Условие(-я) прочности имеет(-ют) вид …
1) 
; 2) 
; 3) , 
; 4) .
3.1. Чистый сдвиг. Расчет на сдвиг (срез)
Задание 3.1.1: Правило, согласно которому на взаимно перпендикулярных площадках элемента, выделенного из тела, касательные напряжения равны по величине и направлены к общему ребру (или от него), называют…
1) масштабным эффектом;
2) законом парности касательных напряжений;
3) законом Гука при сдвиге; 4) условием неразрывности деформаций.
Касательные напряжения, действующие по нижней и верхней грани элемента, образуют пару сил, которая вызывает вращение элемента. Поэтому на боковых гранях элемента возникают такие касательные напряжения, которые должны создавать пару сил противоположного направления.
Задание 3.1.2: При расчете заклепки на срез величина площади среза равна…
1) 
; 2) 
; 3) 
; 4) 
.
Задание 3.1.3: Закон Гука при сдвиге выражается зависимостью…
1) 
; 2) 
; 3) 
; 4) .
Задание 3.1.4: Из расчета на срез минимальная высота головки болта при заданных значениях d и 
равна…
1) 
; 2) 
; 3) 
; 4) 
, тогда 
.
Задание 3.1.5: Напряженное состояние, когда на гранях выделенного элемента возникают только касательные напряжения, называют…
1) линейным; 2) объемным;
3) двухосным растяжением; 4) чистым сдвигом.
1) 
; 2) 
; 3) или 
; 4) 
.
3.2. Крутящий момент. Деформации и напряжения
Задание 3.2.1: Угол закручивания стержня круглого поперечного сечения определяется по формуле…
1) 
; 2) 
; 3) 
; 4) 
.
Задание 3.2.2: При кручении угол взаимного поворота двух сечений, отнесенный к расстоянию между ними, называется…
1) углом сдвига; 2) угловым перемещением;
3) относительным углом закручивания;
4) депланацией поперечного сечения.
Величина 
обозначается обычно через 
и называется относительным углом закручивания. Это угол взаимного поворота двух сечений, отнесенный к расстоянию между ними.
Задание 3.2.3: Напряжение в точке С поперечного сечения определяется по формуле…
1) 0; 2) 
; 3) 
; 4) 
.
.
Задание 3.2.4: Деформацию стержня, при которой в поперечных сечениях возникает только крутящий момент, называют…
1) чистым изгибом; 2) поперечным изгибом;
3) кручением; 4) чистым сдвигом.
Задание 3.2.5: При увеличении момента 
в два раза наибольшие касательные напряжения…
1) уменьшатся в два раза; 2) не изменятся;
3) увеличатся в четыре раза; 4) увеличатся в два раза.
Задание 3.2.6: Труба испытывает деформацию кручение. Эпюра распределения касательных напряжений в поперечном сечении трубы имеет вид …
1) 
; 2) 
; 3) 
; 4) 
3.3. Расчет на прочность при кручении
Задание 3.3.1: Стержень круглого поперечного сечения диаметром d работает на кручение. Касательное напряжение в точке, которая расположена на расстоянии d /4 от оси стержня, равно 
. Наибольшее касательное напряжение в данном поперечном сечении стержня равно…
1) ; 2) 2; 3) 4; 4) 8.
На расстоянии d /4 имеем 
, а на расстоянии d /2
.
Задание 3.3.2: Условие прочности при кручении стержня круглого поперечного сечения с неизменным по длине диаметром имеет вид…
1) 
; 2) 
; 3) 
; 4) 
.
Вдоль любого радиуса касательные напряжения изменяются по линейному закону, достигая максимальных значений в точках у поверхности. Поэтому условие прочности при кручении стержня круглого поперечного сечения с неизменным по длине диаметром имеет вид
, где 
, 
, d – диаметр стержня.
Задание 3.3.3: Из условия прочности, при заданном значении 
, наименьший допускаемый диаметр вала равен… Принять 
.
1) 
; 2) 
; 3) 
; 4) 
.
.
Задание 3.3.4: При кручении максимальное касательное напряжение возникает в точке…
1) 
; 2) 
; 3) 
; 4) 
.
Задание 3.3.6: Труба испытывает деформацию кручение. Касательное напряжение в точке С поперечного сечения трубы равно 20 МПа. Предел текучести материала трубы при чистом сдвиге 
МПа. Коэффициент запаса прочности 
равен …
1) 0,33; 2) 12; 3) 6; 4) 3.
.
3.4. Расчет на жесткость при кручении
Задание 3.4.1: Жесткостью поперечного сечения круглого стержня при кручении называется выражение…
Относительный угол закручивания стержня круглого поперечного сечения определяется по формуле 
. Чем меньше , тем больше жесткость стержня. Поэтому произведение GJ P называется жесткостью поперечного сечения стержня на кручение.
Задание 3.4.2: Стержень круглого сечения диаметром d нагружен, как показано на рисунке. Максимальное значение относительного угла закручивания равно…
1) 
; 2) 
; 3) 
; 4) 
.
При решении задачи воспользуемся формулой для определения
относительного угла закручивания стержня с круглым поперечным сечением, в нашем случае получим 
.
1) 
; 2) 
; 3) 
; 4) 
.
.
1) 
; 2) 
; 3) нулю; 4) 
.
Взаимный угол поворота двух сечений для стержня с круглым сечением определяется по формуле 
. Применительно к данной задаче имеем
.
Задание 3.4.5: Условие жесткости при кручении стержня круглого поперечного сечения, с неизменным по длине диаметром имеет вид…
1) ; 2) 
; 3) 
; 4) 
.
1) 
; 2) 
; 3) 
; 4) 
.
4. Напряженное и деформированное состояние в точке
4.1. Напряженное состояние в точке. Главные площадки и главные напряжения
Задание 4.1.1: Совокупность напряжений, возникающих на множестве площадок, проходящих через рассматриваемую точку, называют …
1) напряженным состоянием в точке; 2) полным напряжением;
3) нормальным напряжением; 4) касательным напряжением.
Задание 4.1.2: Площадки в исследуемой точке напряженного тела, на которых касательные напряжения равны нулю, называют …
1) ориентированными; 2) главными площадками;
3) октаэдрическими; 4) секущими.
При повороте элементарного объема 1 можно отыскать такую его пространственную ориентацию 2, при которой касательные напряжения на его гранях исчезнут и останутся только нормальные напряжения (некоторые из них могут быть равными нулю).
Задание 4.1.3: Главные напряжения для напряженного состояния, показанного на рисунке, равны… (Значения напряжений указаны в МПа ).
1)σ 1 =150 МПа, σ 2 =50 МПа ; 2) σ 1 =0 МПа, σ 2 =50 МПа, σ 3 =150 МПа;
3) σ 1 =150 МПа, σ 2 =50 МПа, σ 3 =0 МПа; 4) σ 1 =100 МПа, σ 2 =100 МПа.
2) σ 1 =150 МПа, σ 2 =-100 МПа, σ 3 =50 МПа;
3) σ 1 =50 МПа, σ 2 =-100 МПа, σ 3 =150 МПа;
4) σ 1 =-100 МПа, σ 2 =50 МПа, σ 3 =150 МПа;
1) 
; 2) 0 0 ; 3) 
; 4) 
.
Угол 
определяется по формуле 
.
Подставляя числовые значения напряжений, получаем 
, 
. Отрицательный угол откладываем по часовой стрелке.
Задание 4.1.6: Значения главных напряжений определяют из решения кубического уравнения 
. Коэффициенты J 1 , J 2 , J 3 называют…
1) инвариантами напряженного состояния; 2) упругими постоянными;
3) направляющими косинусами нормали;
4) коэффициентами пропорциональности.
4.2. Виды напряженного состояния
Задание 4.2.1: Стержень круглого сечения диаметром d испытывает деформации чистого изгиба и кручения. Напряженное состояние в точке В показано на рисунке…
1) 
; 2)
; 3)
; 4)
.
Задание 4.2.2: Стержень испытывает деформации растяжения и чистого изгиба. Напряженное состояние в опасной точке называется…
1) плоским; 2) объемным; 3) линейным; 4) чистым сдвигом.
Следовательно, в опасной точке будет линейное напряженное состояние.
Задание 4.2.3: Напряженное состояние «чистый сдвиг» показано на рисунке…
1)
; 2) 
; 3) 
; 4)
.
Задание 4.2.4: Тип напряженного состояния, показанного на рисунке, называется…
1) линейным; 2) плоским; 3) объемным; 4) чистым сдвигом.
Задание 4.2.5: Напряженное состояние при значениях σ 1 =0 МПа, σ 2 =-20 МПа, σ 3 =-50 МПа называют…
1) объемным; 2) чистым сдвигом; 3) плоским; 4) линейным.
1) линейное; 2) плоское (чистый сдвиг); 3) плоское; 4) объемное.
.
Поставляя числовые значения, получаем 
, 
, 
. Присваивая главным напряжениям индексы, имеем: σ 1 =0 МПа, σ 2 =-50 МПа, σ 3 =-100 МПа.
4.3. Оценка прочности материала при сложном напряженном состоянии. Теории прочности
Задание 4.3.1: Напряженное состояние в точке показано рисунке. Значение эквивалентного напряжения по критерию удельной потенциальной энергии формоизменения (четвертая теория прочности) равно.
1) 
; 2) 
; 3) 
; 4) 
.
.
Для заданного напряженного состояния значения главных напряжений равны σ 1 =σ, σ 2 =0, σ 3 =-σ. После преобразований найдем .
Задание 4.3.2: Число, показывающее, во сколько раз следует одновременно увеличить все компоненты напряженного состояния, чтобы оно стало предельным, называется…
1) коэффициентом запаса для данного напряженного состояния;
2) теоретическим коэффициентом концентрации напряжений;
3) эффективным коэффициентом концентрации напряжений;
4) коэффициентом динамичности системы.
Задание 4.3.3: Напряжение, которое следует создать в растянутом стержне, чтобы его состояние было равноопасно с заданным напряженным состоянием, называют …
1) главным напряжением; 2) наибольшим касательным напряжением;
3) октаэдрическим напряжением; 4) эквивалентным напряжением.
Задание 4.3.4: Состояние, при котором происходит качественное изменение свойств материала, переход от одного механического состояния к другому, называется…
1) хрупкостью; 2) пластичностью;
3) предельным напряженным состоянием; 4) разрушением.
Задание 4.3.5: Изотропный материал на растяжение и сжатие работает неодинаково. Для оценки прочности материала при сложном напряженном состоянии используется теория…
1) О. Мора; 2) наибольших удлинений (вторая теория прочности);
3) наибольших касательных напряжений (третья теория прочности);
4) удельной потенциальной энергии формоизменения (четвертая теория прочности);
Задание 4.3.6: Согласно теории наибольших касательных напряжений (третья теория прочности), самое опасное напряженное состояние показано на рисунке …
1) А; 2) Б; 3) все три напряженных состояния равноопасны; 4) В.
4.4. Деформированное состояние в точке. Связь между деформациями и напряжениями
Задание 4.4.1: Зависимость между компонентами напряженного и деформированного состояния в пределах малых упругих деформаций носит название…
1) принципа Сен-Венана; 2) закона Гука при сдвиге;
3) теоремы Кастилиано; 4) обобщенного закона Гука.
Задание 4.4.2: Совокупность линейных и угловых деформаций, возникающих по различным осям и в различных плоскостях, проходящих через данную точку тела, называют…
1) депланацией; 2) перемещением точки;
3) деформированным состоянием в точке; 4) объемной деформацией.
В общем случае элементарный объем испытывает три линейные деформации и три угловые. Деформированное состояние в точке полностью определяется, если заданы шесть компонентов тензора деформаций (
, 
, 
, 
, 
, 
). Зная эти компоненты, можно определить линейную и угловую деформации в любом направлении и в любой плоскости, проходящей через данную точку.
Задание 4.4.3: Три взаимно перпендикулярные оси, в системе которых отсутствуют угловые деформации, называют…
1) главными осями деформированного состояния;
2) главными осями; 3) центральными осями; 4) осями симметрии.
Задание 4.4.4: Модуль упругости материала Е и коэффициент Пуассона μ заданы. Относительное изменение объема равно …
1) 
; 2) 
; 3) 0; 4) 
.
Задание 4.4.5: На рисунке показано напряженное состояние в точке изотропного тела. Модуль упругости материала 
, коэффициент Пуассона 
. Линейная деформация в направлении х равна…
1) 
; 2) 
; 3) 
; 4) 
.
Задание 4.4.6: Объемный элемент находится под действием нормальных напряжений, показанных на рисунке: 
, 
, 
. Модуль упругости материала 
, коэффициент Пуассона . Линейная деформация в направлении оси z будет равна нулю, когда σ принимает значение…
5. Геометрические характеристики поперечных
5.1. Статические моменты. Центр тяжести плоской фигуры
Задание 5.1.1: Статический момент относительно оси x равен…
В данном случае 
, где А – площадь сечения, 
– ордината центра тяжести сечения.
Задание 5.1.2: Ось, относительно которой статический момент площади сечения равен нулю, называется…
1) осью симметрии; 2) центральной;
3) средней линией контура; 4) нейтральной линией.
Задание 5.1.3: Статический момент площади сечения относительно оси x равен…
1) 
; 2) 0; 3) 
; 4) 
.
.
Задание 5.1.4: Статический момент площади фигуры относительно оси x определяется интегралом …
1) 
; 2) 
; 3) 
; 4) 
.
Задание 5.1.5: Статический момент относительно оси x равен…
1) 
; 2) нулю; 3) 
; 4) 
.
5.2. Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей
Задание 5.2.1: Осевой момент инерции площади сечения относительно оси y равен…
1)
; 2) 
; 3) 
; 4) 
.
Задание 5.2.2: Осевой момент инерции площади фигуры относительно оси y определяется интегралом …
1) ; 2) ; 3) 
; 4) 
.
.
Задание 5.2.3: На рисунке размеры поперечного сечения заданы в см. Осевой момент инерции сечения относительно центральной оси x равен…
1) 
; 2) 
; 3) 
; 4) 
.
.
Задание 5.2.5: Осевой момент инерции относительно оси x 1 равен…
1) 
; 2) 
; 3) 
; 4) 
.
Задание 5.2.6: Осевой момент инерции относительно оси y равен…
1) 
; 2) 
; 3) 
; 4) 
.
5.3. Главные оси и главные моменты инерции
Задание 5.3.1: Для сечения известны осевые моменты инерции сечения относительно осей х 1 , у 1 , х 2 : 
, 
, 
. Осевой момент инерции относительно оси у 2 равен…
Задание 5.3.2: Из указанных центральных осей сечения равнополочного уголка главными являются…
Задание 5.3.3: Главные оси инерции …
1) можно провести только через точки, лежащие на оси симметрии;
2) можно провести только через центр тяжести плоской фигуры;
3) это оси, относительно которых моменты инерции плоской фигуры равны нулю;
4) можно провести через любую точку плоской фигуры.
В курсе сопротивления материалов доказывается, что если эти оси поворачивать, то можно определить такое их положение, при котором центробежный момент инерции площади обращается в ноль, а моменты инерции относительно этих осей принимают экстремальные значения. Такие оси называются главными осями.
Задание 5.3.4: Из указанных центральных осей главными осями сечения являются…
Задание 5.3.5: Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются…
1) центральными осями; 2) осями симметрии;
3) главными центральными осями; 4) главными осями.
,
,
.
При некотором значении угла 
центробежный момент инерции сечения обращается в нуль, а осевые моменты инерции принимают экстремальные значения. Данные оси называются главными осями.
Задание 5.3.6: Момент инерции сечения относительно главной центральной оси х С равен…
1) 
; 2) 
; 3) 
; 4) 
.
Решение: Верный ответ – 2)
Для вычисления 
используем формулу
5.4. Моменты инерции простых и сложных сечений
Задание 5.4.1: Осевой момент инерции относительно оси x равен…
1) 
; 2) 
; 3) 
; 4) 
.
Осевой момент инерции 
. В данном случае
.
Задание 5.4.2: Поперечное сечение балки составлено из вертикального листа и четырех неравнополочных уголков 
. Характеристики уголка заданы. Размеры на рисунке даны в мм. Моменты инерции сечения 
и 
соответственно равны…
Осевой момент инерции относительно оси x определяется по формуле
.
Аналогично определяем осевой момент инерции относительно оси y
Задание 5.4.3: Момент инерции площади фигуры, состоящей из двух кругов, относительно оси x равен…
1) 
; 2) 
; 3) 
; 4) 
.
Задание 5.4.5: Поперечное сечение балки составлено из двух швеллеров №20 и листов, прикрепленных с помощью сварки. Характеристики швеллера приведены. Размеры на рисунке даны в мм. Осевой момент инерции сечения относительно главной центральной оси x равен…
.
Задание 5.4.6: Момент инерции сечения относительно оси х равен…
1) 
; 2) 
; 3) 
; 4) 
.
Для вычисления используем формулу
, 
.