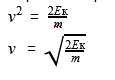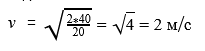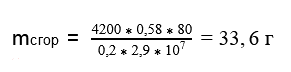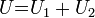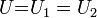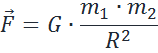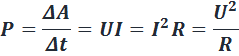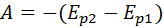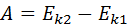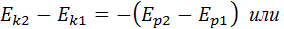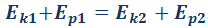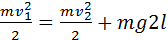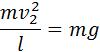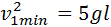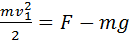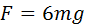в чем заключается закон сохранения механической энергии

Закон сохранения энергии.

Закон сохранения энергии формулируется следующим образом: полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения и упругости, остается неизменной.

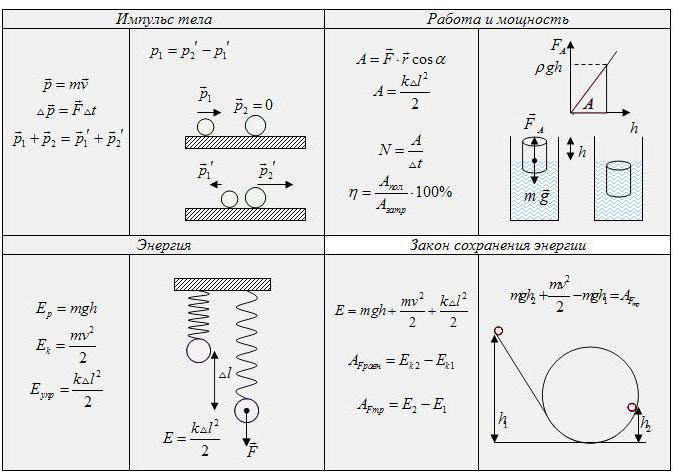
Под полной механической энергией понимаем сумму кинетической и потенциальной энергий тел. Кинетическая энергия характеризует движущиеся тела, потенциальная энергия – взаимодействующие тела. Обе энергии изменяются только в результате взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля. Если несколько тел в замкнутой системе (когда на них не действуют никакие внешние силы) взаимодействуют между собой только силами тяготения и силами упругости, то при любых взаимодействиях тел работа сил упругости (сил тяготения) равна изменению потенциальной энергии, взятому с противоположным знаком:

А по теореме о кинетической энергии работа этих же сил равна изменению кинетической энергии:

Сравнив оба равенства, получим:

т.е. изменение кинетической энергии и изменение потенциальной энергии тел в замкнутой системе равны друг другу по абсолютному значению, но имеют противоположные знаки.

Если кинетическая энергия тел увеличивается, то их потенциальная энергия на столько же уменьшается, и наоборот. Другими словами, происходит как бы превращение одного вида энергии в другой:

Превращение потенциальной энергии в кинетическую и наоборот – главное отличительное свойство энергии.

Источник

Закон сохранения механической энергии

Энергия: что это такое

Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно.

Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.

Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.

Механическая энергия

Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.

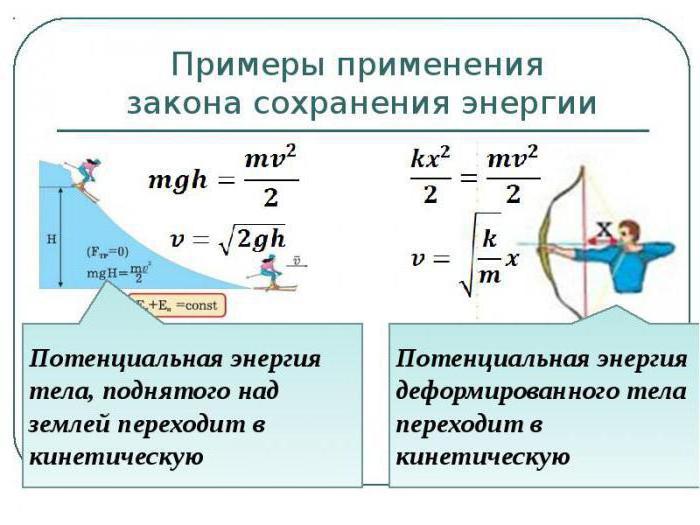
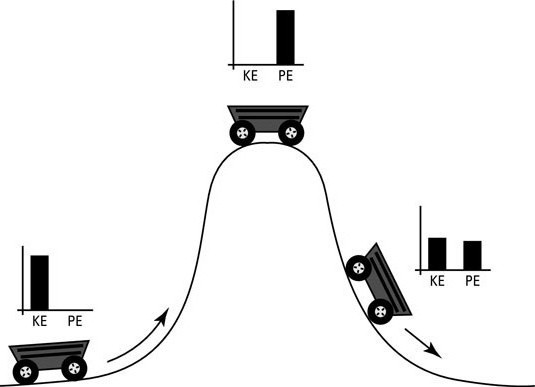
Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.

Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим 😂), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.

Кинетическая энергия

Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.

Кинетическая энергия

Ек = (m*v^2)/2

Ек — кинетическая энергия [Дж]

Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.

Задачка раз

Определить кинетическую энергию собаченьки массой 10 килограмм, если она бежала за мячом с постоянной скоростью 2 м/с.

Решение:

Формула кинетической энергии Ек = (m*v^2)/2

Ответ: кинетическая энергия пёсы равна 20 Дж.

Задачка два

Найти скорость бегущего по опушке гнома, если его масса равна 20 килограммам, а его кинетическая энергия — 40 Дж

Решение:

Формула кинетической энергии Ек = (m*v^2)/2

Ответ: гном бежал со скоростью 2 м/с.

Потенциальная энергия

В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.

Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.

Потенциальная энергия деформированной пружины

Еп — потенциальная энергия [Дж]

x — удлинение пружины [м]

Потенциальная энергия

Еп = mgh

Еп — потенциальная энергия [Дж]

g — ускорение свободного падения [м/с^2]

На планете Земля g ≃ 9,8 м/с^2

Задачка раз

Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с^2.

Решение:

Формула потенциальной энергии Еп = mgh

Eп = 0,1 * 9,8 * 2500=2450 Дж

Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.

Задачка два

Найти высоту горки, с которой собирается скатиться лыжник массой 65 килограмм, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с^2.

Решение:

Формула потенциальной энергии Еп = mgh

Переведем 637 кДж в Джоули.

637 кДж = 637000 Дж

h = 637 000/(65 * 9,8) = 1000 м

Ответ: высота горы равна 1000 метров.

Задачка три

Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E1 и E2. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.

Решение:

Потенциальная энергия вычисляется по формуле: E = mgh

Таким образом, получим, что

Ответ: E1 = E2.

Закон сохранения энергии

В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.

Закон сохранения энергии

Полная механическая энергия замкнутой системы остается постоянной.

Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:

Закон сохранения энергии

Еполн.мех. = Еп + Eк = const

Еполн.мех. — полная механическая энергия системы [Дж]

Еп — потенциальная энергия [Дж]

Ек — кинетическая энергия [Дж]

const — постоянная величина

Задачка раз

Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?

Решение:

Должен выполняться закон сохранения энергии:

В начальный момент времени высота равна нулю, значит Еп = 0. В этот же момент времени Ек максимальна.

В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.

Это можно описать соотношением:

Еп1 + Ек1 = Еп2 + Ек2

Разделим на массу левую и правую часть

Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.

Ответ: высота увеличится в 4 раза

Задачка два

Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?

Решение

По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Емех = Еп = mgh0.

Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Емех = mgh0.

Ответ: Емех = mgh0.

Задачка три

Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.

Решение:

Переведем массу из граммов в килограммы:

У поверхности земли полная механическая энергия мяча равна его кинетической энергии:

Е = Ек0 = (m*v^2)/2 = (0,1*6^2)/2 = 1,8 Дж

На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:

mgh = E — (m*v^2)/2 = 1,8 — (0,1 * 2^2)/2 = 1,6 Дж

h = E/mg = 1,6/0,1*10 = 1,6 м

Ответ: мяч имел скорость 2 м/с на высоте 1,6 м

Переход механической энергии во внутреннюю

Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.

Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.

Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.

Задачка

Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?

Решение:

В самом начале у мяча есть только кинетическая энергия, то есть Емех = Ек.

В конце механическая энергия равна половине начальной, то есть Емех/2 = Ек/2

Часть энергии уходит во внутреннюю, значит Еполн = Емех/2 + Евнутр

Емех = Емех/2 + Евнутр

Ответ: во внутреннюю перейдет половина начальной кинетической энергии

Закон сохранения энергии в тепловых процессах

Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.

Вот что сформулировал Фурье:

При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия.

Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.

Дальше Карно установил, что тепловую энергию, которой обладает на­гретое тело, непосредственно невозможно превратить в механиче­скую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.

Закон сохранения энергии в тепловых процессах

При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом.

Математически его можно описать так:

Уравнение теплового баланса

Q отд = Q пол

Qотд — отданное системой количество теплоты [Дж]

Q пол — полученное системой количество теплоты [Дж]

Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:

Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.

Задачка раз

Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.

Удельная теплота сгорания спирта 2,9·10^7Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С).

Решение:

При нагревании тело получает количество теплоты

где c — удельная теплоемкость вещества

При сгорании тела выделяется энергия

где q — удельная теплота сгорания топлива

По условию задачи нам известно, что на нагревание пошло 20% затраченной энергии.

Ответ: масса сгоревшего топливаа равна 33,6 г.

Задачка два

Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг*℃, удельная теплота плавления льда равна 3,3*10^5 Дж/кг.

Решение:

Для нагревания льда до температуры плавления необходимо:

Qнагрев = 2100 * 0,5 * (10-0) = 10500 Дж

Для превращения льда в воду:

Qпл = 3,3 * 10^5 * 0,5 = 165000 Дж

Q = Qнагрев + Qпл = 10500 + 165000 = 175500 Дж = 175,5 кДж

Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.

Источник

Закон сохранения энергии

Из Википедии — свободной энциклопедии

Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда закономерность, его можно именовать не законом, а принципом сохранения энергии.

С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимости законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря, различающимся для разных систем.

В различных разделах физики по историческим причинам закон сохранения энергии формулировался независимо, в связи с чем были введены различные виды энергии. Возможен переход энергии из одного вида в другой, но полная энергия системы, равная сумме отдельных видов энергий, сохраняется. Однако, из-за условности деления энергии на различные виды, такое деление не всегда может быть произведено однозначно.

Для каждого вида энергии закон сохранения может иметь свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон сохранения механической энергии, в термодинамике — первое начало термодинамики, а в электродинамике — теорема Пойнтинга.

С математической точки зрения, закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени.

Источник

Закон сохранения энергии заключается в том что. Закон изменения и сохранения полной механической энергии

Механическая энергия. Закон сохранения механической энергии. Применение закона

Что такое механическая энергия? Закон сохранения механической энергии связывает между собой разные виды энергии, рассмотрим их подробнее. Выясним и возможности его практического применения.

Особенности физической системы

Математическая формулировка закона сохранения механической энергии связывает кинетическую и потенциальную энергию.

Суть закона заключается в том, что допускается превращение одной формы в иной вид, при этом суммарное значение остается неизменной величиной. В разных разделах физики есть свои формулировки данного закона. Например, в термодинамике выделяют первое начало, в классической механике используют закон сохранения, а в электродинамике расчеты проводят на основе теоремы Пойнтинга.

Фундаментальный смысл

Как определяется механическая энергия? Закон сохранения механической энергии объясняют теоремой Нетер. Она объясняет независимость закона относительно временных рамок, иных основополагающих принципов механики. Ньютоновская теория характеризуется использованием частного случая закона сохранения энергии.

Как можно качественно описать данный закон? Сумма потенциальной и кинетической форм в замкнутой системе сохраняется неизменной.

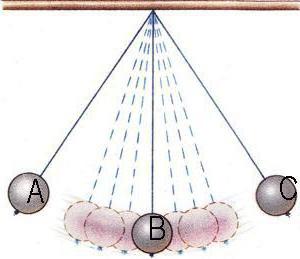
Если на систему не действуют иные силы, в таком случае не наблюдается ее исчезновения, а также появления. Как осуществлялось обоснование закона сохранения механической энергии? Лабораторная деятельность многих ученых основывалась на изучении перехода кинетической энергии в потенциальный вид. Например, при анализе состояния математического маятника удалось подтвердить неизменность суммарного значения двух видов.

Основы термодинамики

Как рассчитывается механическая энергия? Закон сохранения механической энергии можно применить к первому началу термодинамики. Рассматривается изменение внутренней энергии системы в процессе ее перехода из одного состояния в иное через сумму количества теплоты, передаваемого системе, и работы внешних сил.

Закон сохранения импульса и механической энергии поясняет сложность получения двигателя, работающего постоянно.

Изучение свойств жидкостей

Для гидродинамики идеальных жидкостей было выведено уравнение Бернулли. Суть его в постоянстве жидкости, имеющей однородную плотность.

Как изучалась механическая энергия? Закон сохранения механической энергии был определен экспериментальным путем. Гей-Люссак в начале 19 века пытался найти зависимость между расширением газа и его теплоемкостью. Ему удалось установить неизменность температуры в рассматриваемом процессе.

История появления закона

В 19 веке, после опытов М. Фарадея, была выявлена зависимость между разными видами материи. Именно эти исследования стали основой для появления закона сохранения. Что такое полная механическая энергия? Закон сохранения энергии назван результатом опытов, проведенных французским физиком Сади Карно. Он пытался экспериментальным путем определить зависимость между работой, совершенной над системой, и выделяющимся количеством теплоты.

Именно Карно удалось установить зависимость между теплом и работой, то есть сформулировать первое начало термодинамики на основе закона сохранения. Джеймс Прескотт Джоуль провел серию классических опытов, направленных на количественное определение теплоты, выделяющейся при вращении в электромагнитном поле соленоида с металлическим сердечником.

Ему удалось установить, что количество теплоты, выделяемой в экспериментах, прямо пропорционально значению тока, взятому в квадрате. В последующих экспериментах Джоуль поменял катушку на груз, падающий с некоторой высоты. Ученому удалось установить зависимость между величиной выделяемого тепла и математическим показателем энергии груза.

Роберт Майер предложил интересную гипотезу универсального применения закона сохранения энергии. Занимаясь изучением функционирования систем человека, немецкий врач решил проанализировать то количество теплоты, которое организм выделяет по мере переработки пищи. Его интересовала величина работы, совершаемой в этом случае. Майеру удалось установить связь между теплом, работой, подтверждающую возможность использования закона сохранения энергии для процессов, происходящих внутри организма человека.

Герман Гельмгольц дал первую характеристику потенциальной энергии, основываясь на исследованиях Джоуля и Майера. Он в своих рассуждениях базировался на связи кинетической (живой) энергии с силами напряжения (потенциальной энергии).

Заключение

Закон, поясняющий неизменность суммарного показателя нескольких видов энергии, присущих для рассматриваемой системы, сохраняет свою актуальность и в настоящее время. Открытие закона способствовало развитию физических наук, стало отправной точкой для инновационных процессов, рассматриваемых в науке и технике. Именно изучение закона сохранения механической энергии, лабораторная практика стали детальным обоснованием единства живой природы.

Он указывает на закономерность перехода одной формы в другую, раскрывает глубину внутренних связей между формами материи. Любое явление, происходящее в живой и неживой природе, легко можно объяснить с помощью данного закона. В школьной программе уделяется особое внимание выводу математической записи связи между разными видами движения, рассматриваются основы термодинамической системы. На едином государственном экзамене по физике предлагаются задачи, предполагающие использование данного соотношения.

Процессы, которые происходят в Солнечной системе, связанные с изменением положения тел за определенный промежуток времени, могут быть объяснены с точки зрения основных физических правил. Переход из кинетической в потенциальную форму актуален при изучении механического движения тел. Зная, что суммарный показатель будет постоянным, можно проводить математические вычисления.

Закон изменения и сохранения полной механической энергии;

Полной механической энергией системы тел называется сумма кинетической и потенциальной энергий:

Очевидно, что изменение полной механической энергии равно:

E = E_п + E_к

Тре́ние— процесс взаимодействия тел при их относительном движении (смещении) либо при движении тела в газообразной или жидкой среде. По-другому называется фрикционным взаимодействием (англ. friction). Изучением процессов трения занимается раздел физики, который называется механикой фрикционного взаимодействия, или трибологией.

Трение главным образом имеет электронную природу при условии, что вещество находится в нормальном состоянии. В сверхпроводящем состоянии вдалеке от критической температуры основным «источником» трения являются фононы, а коэффициент трения может уменьшиться в несколько раз. В физике механическая энергия описывает сумму потенциальной и кинетической энергии, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу. Закон сохранения механической энергии утверждает, что если тело или система подвергается действию только консервативных сил, то полная механическая энергия этого тела или системы остаётся постоянной. В изолированной системе, где действуют только консервативные силы, полная механическая энергия сохраняется

2. Последовательное и параллельное соединение проводников. Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.

При последовательном соединении проводников сила тока во всех проводниках одинакова.

При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

При последовательном соединении проводников сила тока в любых частях цепи одна и та же:

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:

Резистор:

Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках:

Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же:

При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению:

1. Закон всемирного тяготения и движение искусственных спутников. В рамках классической механики гравитационное взаимодействие описывается законом всемирного тяготения. Этот закон был открыт Ньютоном в 1666 г.. Он гласит, что сила гравитационного притяжения между двумя материальными точками массы и , разделёнными расстоянием , пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:

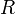
Здесь G — гравитационная постоянная, равная м³/(кг с²).

Скорость, которую нужно сообщить телу для того, чтобы оно стало искусственным спутником Земли, называютпервой космической скоростью. Реактивный двигатель — это двигатель, преобразующий химическую энергию топлива в кинетическую энергию газовой струи, при этом двигатель приобретает скорость в обратном направлении. К. Э. Циолковский вывел формулу, позволяющую рассчитать максимальную скорость, которую может развить ракета. Максимально достижимая скорость зависит в первую очередь от скорости истечения газов из сопла, которая в свою очередь зависит прежде всего от вида топлива и температуры газовой струи. Чем выше температура, тем больше скорость. Значит, для ракеты нужно подбирать самое калорийное топливо, дающее наибольшее количество теплоты. Отношение массы топлива к массе ракеты в конце работы двигателя (т.е. по существу к весу пустой ракеты) называется числом Циолковского. Основной вывод состоит в том, что в безвоздушном пространстве ракета разовьёт тем большую скорость, чем больше скорость истечения газов и чем больше число Циолковского.Закон Циолковского.Применив уравнение Мещерского к движению ракеты, на которую не действуют внешние силы, и проинтегрировав уравнение, получим формулу Циолковского:

Релятивистское обобщение этой формулы имеет вид:

, где — скорость света.

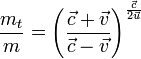
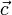
Ракетный двигатель — реактивный двигатель, источник энергии и рабочее тело которого находится в самом средстве передвижения. Ракетный двигатель — единственный практически освоенный для вывода полезной нагрузки на орбиту искусственного спутника Земли и применения в условиях безвоздушного космического пространства тип двигателя. Другие типы двигателей, пригодные для применения в космосе (например, солнечный парус, космический лифт) пока еще не вышли из стадии теоретической и/или экспериментальной отработки.

Сила тяги в ракетном двигателе возникает в результате преобразования исходной энергии в кинетическую энергию реактивной струи рабочего тела. В зависимости от вида энергии, преобразующейся в кинетическую энергию реактивной струи, различают химические ракетные двигатели, ядерные ракетные двигатели и электрические ракетные двигатели.

Характеристикой эффективности ракетного двигателя является удельный импульс (в двигателестроении применяют несколько другую характеристику — удельная тяга) — отношение количества движения, получаемого ракетным двигателем, к массовому расходу рабочего тела. Удельный импульс имеет размерность м/c, то есть размерность скорости. Для идеального ракетного двигателя удельный импульс численно равен скорости истечения рабочего тела из сопла.

Наиболее распространены химические ракетные двигатели, в которых, в результате экзотермической химической реакции горючего и окислителя (вместе именуемые топливом), продукты сгорания нагреваются в камере сгорания до высоких температур, расширяясь, разгоняются в сверхзвуковом сопле и истекают из двигателя. Топливо химического ракетного двигателя является источником как тепловой энергии, так и газообразного рабочего тела, при расширении которого его внутренняя энергия преобразуется в кинетическую энергию реактивной струи.

Ядерный ракетный двигатель — реактивный двигатель, рабочее тело в котором (например, водород, аммиак и др.) нагревается за счет энергии, выделяющейся при ядерных реакциях (распада или термоядерного синтеза). Различают радиоизотопные, ядерные и термоядерные ракетные двигатели.

Ядерные ракетные двигатели позволяют достичь значительно более высокого (по сравнению с химическими ракетными двигателями) значения удельного импульса благодаря большой скорости истечения рабочего тела (от 8 000 м/с до 50 км/с и более). Вместе с тем, общая тяга ЯРД может быть сравнима с тягой химических ракетных двигателей, что создает предпосылки для замены в будущем химических ракетных двигателей ядерными. Основной проблемой при использовании ЯРД является радиоактивное загрязнение окружающей среды факелом выхлопа двигателя, что затрудняет использование ЯРД (кроме, возможно, газофазных — см. ниже), на ступенях ракет-носителей, работающих в пределах земной атмосферы. Впрочем, конструктивно совершенный ГФЯРД, исходя из его расчётных тяговых характеристик, может легко решить проблему создания полностью многоразовой одноступенчатой ракеты-носителя.

2. Работа и мощность электрического тока. При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном участке совершает работу

где U = Δφ12 – напряжение. Эту работу называют работой электрического тока.

Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:

Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).

1. Статика. Статика (от греч. στατός, «неподвижный») — раздел механики, в котором изучаются условия равновесия механических систем под действием приложенных к ним сил и моментов. Система сил, приложенная к телу или материальной точке, называется уравновешенной или эквивалентной нулю, если тело под действием этой системы находится в состоянии покоя или движения по инерции.[1]

· Не нарушая механического состояния тела, к нему можно приложить или отбросить уравновешенную систему сил.

· О действии и противодействии. При всяком действии одного тела на другое со стороны другого тела имеется противодействие, такое же по величине, но противоположное по направлению.

· О двух силах. Две силы, приложенные к одному и тому же телу, взаимно уравновешены (их действие эквивалентно нулю) тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны.

· О равнодействующей. Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и равна диагонали параллелограмма, построенного на этих силах как сторонах.

· Аксиома затвердевания. Если деформируемое тело находилось в равновесии, то оно будет находиться в равновесии и после его затвердевания.

· Аксиома о связях. Механическое состояние системы не изменится, если освободить её от связей и приложить к точкам системы силы, равные действовавшим на них силам реакций связей.

Закон сохранения механической энергии

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел (см 1.19):

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

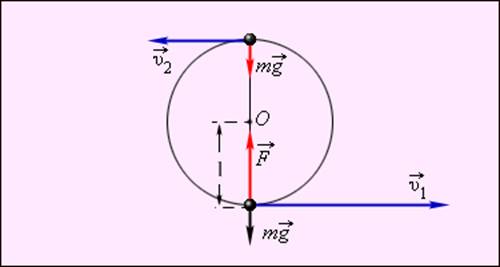
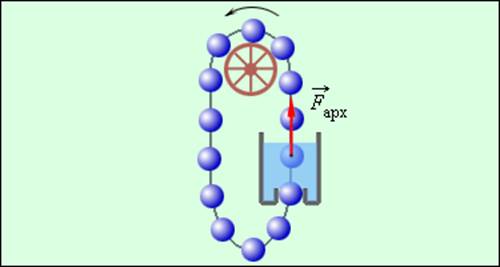
Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости (задача Гюйгенса). Рис. 1.20.1 поясняет решение этой задачи.

К задаче Христиана Гюйгенса. 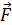– сила натяжения нити в нижней точке траектории

Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:

Обратим внимание на то, что сила 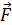натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.

При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:

Из этих соотношений следует:

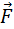
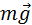
Центростремительное ускорение в нижней точке создается силами и направленными в противоположные стороны:

Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно

Прочность нити должна, очевидно, превышать это значение.

Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.

В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.

Сила трения не является консервативной. Работа силы трения зависит от длины пути.

Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).

При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую.

Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.

Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии (рис. 1.20.2).

Один из проектов «вечного двигателя». Почему эта машина не будет работать?

История хранит немалое число проектов «вечного двигателя». В некоторых из них ошибки «изобретателя» очевидны, в других эти ошибки замаскированы сложной конструкцией прибора, и бывает очень непросто понять, почему эта машина не будет работать. Бесплодные попытки создания «вечного двигателя» продолжаются и в наше время. Все эти попытки обречены на неудачу, так как закон сохранения и превращения энергии «запрещает» получение работы без затраты энергии.

Источник