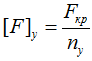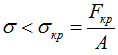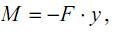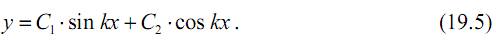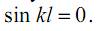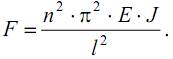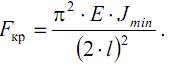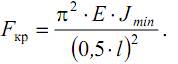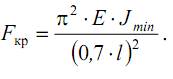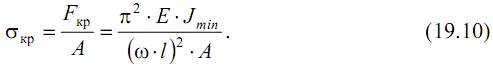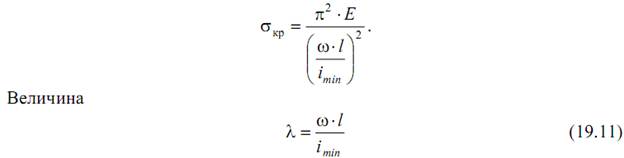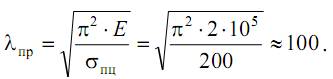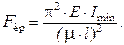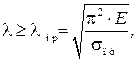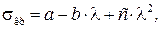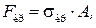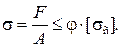в чем заключается условие устойчивости сжатого стержня
iSopromat.ru
Устойчивостью сжатых стержней называют их способность восстанавливать начальную прямолинейную форму после снятия продольной сжимающей нагрузки.
При сжатии длинных стержней их продольная ось искривляется. Такой вид деформации называется продольным изгибом.
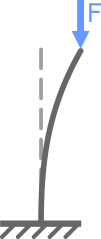
Прямолинейный центрально сжатый стержень при определенной нагрузке (силе F) может оказаться в опасном (критическом) состоянии, при котором форма продольной оси стержня будет неустойчива.
В этом случае сколь угодно малые случайные воздействия могут вызвать большие отклонения от его первоначальной формы, вследствие чего стержень после устранения возмущений (снятия внешних нагрузок) останется в изогнутом состоянии.
Такое состояние называют потерей устойчивости прямолинейной формы стержня.
Нагрузка, при которой прямолинейная форма перестает быть формой устойчивого равновесия называется критической (Fкр).
Таким образом, исследование устойчивости стержня заключается в определении величины критической сжимающей силы Fкр.
Для обеспечения устойчивости допускаются нагрузки, составляющие лишь определенную часть от критических и называемые допустимыми силами [F]у.
здесь, nу – коэффициент запаса устойчивости, зависит от материала стержня.
Рекомендуемые значения коэффициента устойчивости находятся в пределах:
Поперечные сечения сжатых стержней должны назначаться не из условия прочности от чистого сжатия, а из условия того, чтобы сжимающие напряжения были меньше критических напряжений:
где A – площадь поперечного сечения стержня.
Критическая сила определяется по формуле Эйлера.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
19.1. Основные понятия. Устойчивое и неустойчивое равновесие
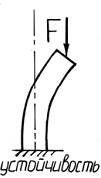
Устойчивость– способность тела сохранять положение или форму равновесия при внешних воздействиях.
Обычно потеря устойчивости системы сопровождается большими перемещениями, возникновением пластических деформаций или разрушением. Возможны также случаи, когда система, потеряв устойчивость, переходит в режим незатухающих колебаний. Особая опасность потери устойчивости заключается в том, что она происходит внезапно и при низких значениях напряжений, когда прочность материала еще далеко не исчерпана.
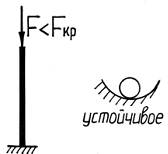
При устойчивом равновесии тело, выведенное какой-либо силой из своего первоначального положения, возвращается в это положение после прекращения действия силы.
При неустойчивом равновесии тело, выведенное какой-либо силой из своего первоначального положения, продолжает деформироваться в направлении данного ему отклонения, и, после удаления внешнего воздействия, в исходное состояние не возвращается. В этом случае
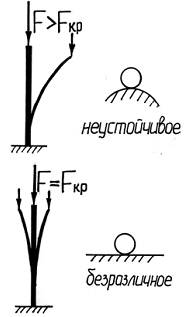
Критическая сила (Fкр) – нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы (положения) тела.
С момента наступления критического состояния до момента разрушения деформации системы нарастают крайне быстро, и практически нет времени принять меры по предотвращению грозящей катастрофы. Таким образом, при расчете на устойчивость критическая нагрузка подобна разрушающей при расчете на прочность.
При этом условие устойчивости можно записать в следующем виде:
19.2. Устойчивость сжатого стержня. Задача Эйлера
При определении критической силы, вызывающей потерю устойчивости сжатого стержня, предполагается, что стержень идеально прямой и сила F приложена строго центрально.
Рассматриваемый метод решения основан на том, что при достижении силой F критического состояния (F=Fкр) стержень находится в безразличном состоянии и ему присущи две формы равновесия: прямолинейная и криволинейная (в таких случаях говорят, что происходит ветвление, или бифуркация, равновесных состояний). Для выявления криволинейной формы равновесия достаточно приложить к стержню малую поперечную возмущающую нагрузку Q, которая вызовет малый прогиб. Если F Fкр, то равновесие стержня становится неустойчивым и сколь угодно малое возмущение достаточно для того, чтобы возникли большие прогибы. Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил академик Петербургской Академии наук Л. Эйлер в 1744 году.
Рассмотрим шарнирно опертый по концам стержень, сжатый продольной силой F. Положим, что по какой-то причине стержень получил малое искривление оси, вследствие чего в нем появился изгибающий момент M:
где y – прогиб стержня в произвольном сечении с координатой x.
Для определения критической силы можно воспользоваться приближенным дифференциальным уравнением упругой линии:
где E – модуль Юнга; J – осевой момент инерции сечения стержня относительно оси z в данном случае; E·J – жесткость стержня при изгибе. Знаки левой и правой части (19.2) согласованны в данной системе координат.
Подставив в это уравнение выражение для изгибающего момента (19.1), получим
Общий интеграл полученного однородного дифференциального уравнения представляется функцией
Это решение содержит три неизвестные: постоянные интегрирования С1 и С2 и параметр k. Найдем эти величины из граничных условий – условий закрепления стержня по концам:
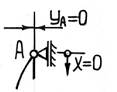
Уравнение (19.6) указывает на то, что при продольном изгибе изогнутая ось стержня может быть представлена как некоторое число волн синусоиды с амплитудой C1.
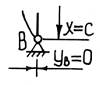
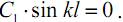
Из свойств синусоиды следует, что
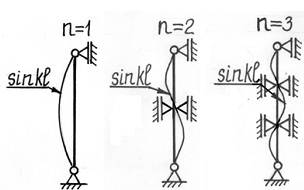
Решая совместно уравнения (19.4) и (19.7), получим выражение для некоторых фиксированных значений сжимающей силы, при которых возможна криволинейная форма равновесия оси стержня
Как видим, минимальное значение критическая сила примет при n=1 (на длине стержня укладывается одна полуволна синусоиды) и J=Jmin (стержень искривляется относительно оси с наименьшим моментом инерции)
19.3. Зависимость критической силы от условий закрепления стержня
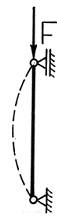
Рассмотрим некоторые характерные случаи закрепления стержня по концам и получим общую формулу для различных видов закрепления.
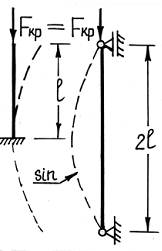
Стержень длиной l заделан одним концом и сжат продольной силой. Из сравнения вида изогнутой оси балки для рассматриваемого и основного случаев можем сделать вывод, что ось стержня, заделанного одним концом, находится в тех же условиях, как и верхняя половина шарнирно опертого стержня длиной 2·l. Таким образом, критическая сила для стержня длиной l с одним защемленным концом может быть найдена так же как и для шарнирно опертой балки длиной 2·l, то есть
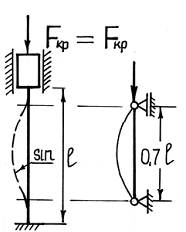
Стержень длиной l, у которого оба конца жестко заделаны. Из сравнения вида изогнутой оси балки для рассматриваемого и основного случаев, а также из соображений симметрии, можем сделать вывод, что средняя часть стержня с заделанными концами, находится в тех же условиях, как и шарнирно опертая балка длиной l/2.
Таким образом, критическая сила для стержня длиной l с двумя защемленными концами может быть найдена так же как и для шарнирно опертой балки длиной l/2, то есть
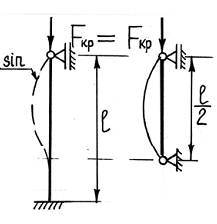
Стержень длиной l, у которого один конец жестко заделан, а другой шарнирно оперт. Из сравнения вида изогнутой оси балки для рассматриваемого и основного случаев, можем сделать вывод, что часть стержня находится в тех же условиях, как и шарнирно опертая балка длиной 0,7·l. Таким образом, критическая сила для стержня длиной l с защемленным и шарнирно опертым концами может быть найдена так же как и для шарнирно опертой балки длиной 0,7·l, то есть
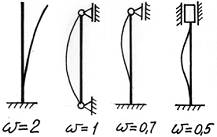
Все полученные выражения можно объединить в одну общую формулу
где ω·l=lпр – приведенная длина стержня; l – фактическая длина стержня; ω – коэффициент приведенной длины, показывающий во сколько раз необходимо изменить длину стержня, чтобы критическая сила для этого стержня стала равна критической силе для шарнирно опертой балки.
19.4. Критические напряжения. Расчет на устойчивость стержня при упруго-пластических деформациях
Вспомним, что 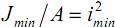
называется гибкостью стержня.
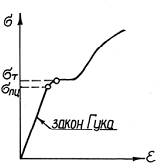
Используя это соотношение, можно найти условие для определения предельной гибкости стержня λпр, когда еще возможно применение формулы Эйлера:
Например, для малоуглеродистых сталей (E=2·105 МПа, σпц≈200 МПа) предельная гибкость
Итак, при λ>λпр для определения критической силы будем пользоваться формулой Эйлера, если же λ
| | | следующая лекция ==> |
| ФОТОТРАНЗИСТОРЫ | | |
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Глава 9. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ



Под действием сжимающей силы стержень может утратить первоначальную форму равновесия и искривиться. Произойдет потеря устойчивости стержня. Наименьшая сила, при которой происходит потеря устойчивости, называется критической и определяется по формуле Эйлера:
где Е – модуль упругости материала стержня;
Imin– минимальный осевой момент инерции сечения стержня;
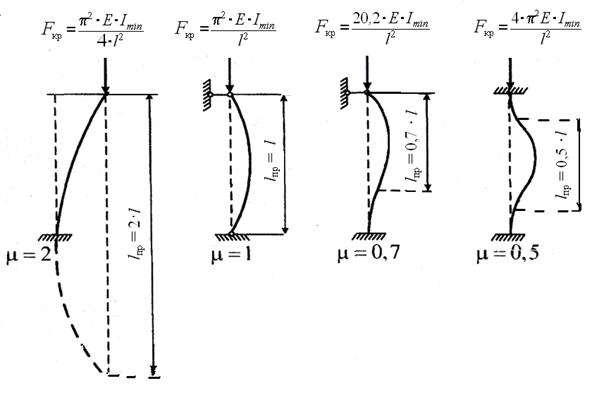
μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня (рис. 38);
l – длина стержня, μ ∙ l = lпр – приведенная длина стержня.
Рис. 38. Значения коэффициента μ приведенной длины и критической
силы Fкр для сжатых стержней при различных способах закрепления концов
Напряжения, вызванные критической силой, называются критическими и определяются по формуле Эйлера:
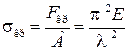
где λ – гибкость стержня, 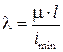
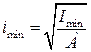
А – площадь поперечного сечения стержня.
Формула Эйлера применима при условии, что критическое напряжение не превышает предела пропорциональности материала 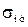
где 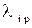
Формулой Эйлера можно пользоваться, если гибкость стержня 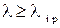
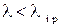
При значениях гибкости от 0 до 40 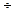
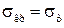
При значениях гибкости, лежащих в интервале 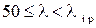
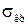
где а, b, с – коэффициенты, зависящие от материала и имеющие размерность напряжения. Они приведены в табл. 12.
Опытные коэффициенты для определения 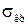
| Материал | а | b | с |
| Сталь Ст3 Сталь Ст5 Чугун Сосна (сжатие вдоль волокон) | 29,3 | 1,14 3,62 0,194 | 0,053 |
Критическая сила является недопустимой для сжатых стержней.
Определение допускаемой сжимающей силы [F] производят двумя способами. Первый способ используется, когда для рассчитываемого стержня известны длина, способ закрепления концов, форма и размеры поперечного сечения, материал, коэффициент запаса на устойчивость. Вначале определяют критическую силу Fкр = sкр ∙ А, а затем допускаемую силу [F]:
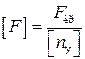
где [nу] – допускаемый коэффициент запаса на устойчивость.
Значения допускаемых коэффициентов запаса на устойчивость [nу] для различных материалов приведены в табл. 13.
Допускаемые коэффициенты запаса на устойчивость
для различных материалов
| Материал | [ny] |
| Сталь Ст 3 | 1,8 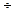 3 3 |
| Сталь Ст 5 | 1,8 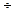 3 3 |
| Чугун | 5 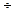 5,5 5,5 |
| Сосна (сжатие вдоль волокон) | 2,8 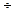 3,2 3,2 |
Второй способ основан на применении таблиц j (l). Сначала определяют гибкость стержня λ, затем по таблице находят j (l) и вычисляют [F] по формуле
где j – коэффициент уменьшения допускаемого напряжения при сжатии [sс].
Значения коэффициента j в зависимости от гибкости λ и материала стержня приведены в табл. 14.
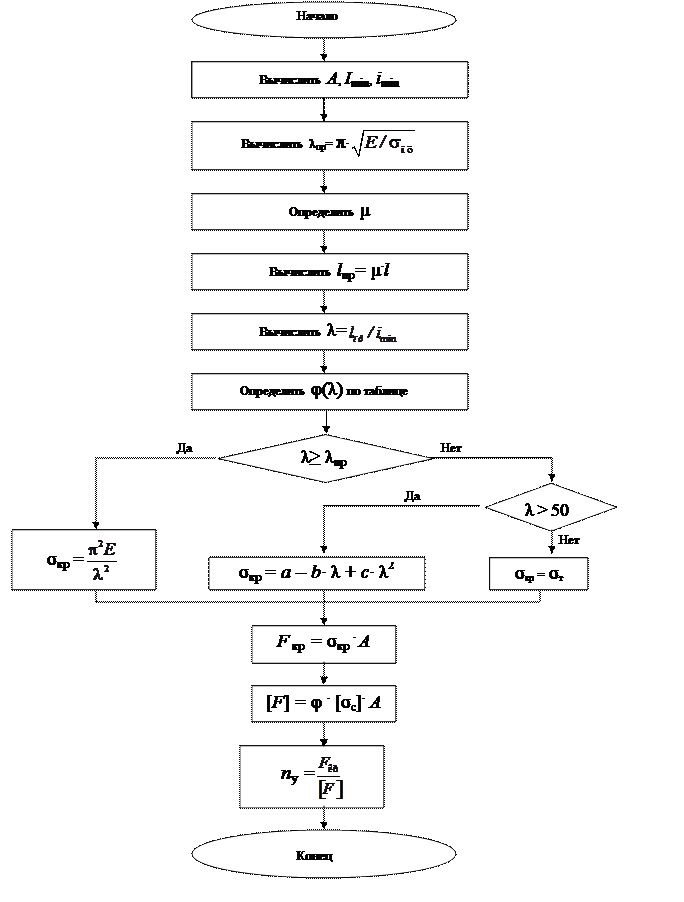
Для расчета критического напряжения, критической силы, допускаемой сжимающей силы и коэффициента запаса на устойчивость
можно использовать блок-схему, представленную на рис. 39.
Значение коэффициента продольного изгиба j (l)
для различных материалов
| Гибкость λ | Значение j (l) | ||
| Сталь Ст3, Ст4 | Сталь Ст5 | Чугун | Дерево |
| 1,00 | 1,00 | 1,00 | 1,00 |
| 0,99 | 0,98 | 0,97 | 0,99 |
| 0,97 | 0,96 | 0,91 | 0,97 |
| 0,95 | 0,93 | 0,81 | 0,93 |
| 0,92 | 0,89 | 0,69 | 0,87 |
| 0,89 | 0,85 | 0,57 | 0,80 |
| 0,86 | 0,80 | 0,44 | 0,71 |
| 0,81 | 0,74 | 0,34 | 0,60 |
| 0,75 | 0,67 | 0,26 | 0,48 |
| 0,69 | 0,59 | 0,20 | 0,38 |
| 0,60 | 0,50 | 0,16 | 0,31 |
| 0,52 | 0,43 | – | 0,25 |
| 0,45 | 0,37 | – | 0,22 |
| 0,40 | 0,32 | – | 0,18 |
| 0,36 | 0,28 | – | 0,16 |
| 0,32 | 0,25 | – | 0,14 |
| 0,29 | 0,23 | – | 0,12 |
| 0,26 | 0,21 | – | 0,11 |
| 0,23 | 0,19 | – | 0,10 |
| 0,21 | 0,17 | – | 0,09 |
| 0,19 | 0,15 | – | 0,08 |
| 0,17 | 0,14 | – | – |
| 0,16 | 0,13 | – | – |
Практически расчет на устойчивость ведется с использованием коэффициента j – коэффициента уменьшения допускаемого напряжения при сжатии [sс].
Условие устойчивости имеет вид
Расчет на устойчивость сводится к недопущению потери устойчивости, т.е. искривления стержня.
Подбор поперечного сечения стержня при заданных длине, сжимающей силе и материале выполняется с использованием таблиц значений j (l) методом последовательных приближений в следующем порядке.
1. Задают произвольное значение j. Например, полагают j = 0,5.
2. Вычисляют допускаемое напряжение на устойчивость:
3. Определяют площадь поперечного сечения из условия
4. Подбирают размеры сечения или номер профиля. Вычисляют
площадь А, минимальный момент инерции Imin, минимальный радиус инерции iminпоперечного сечения.
5. Определяют гибкость стержня l.
6. Если гибкость стержня l > 220, то считают, что заданная сила
F равна допускаемой [F]:
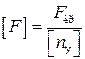
где Fкр – критическая сила (определяется по формуле Эйлера), а nу – коэффициент запаса на устойчивость (выбирается по табл. 13).
Тогда можно определить значение наименьшего момента инерции Imin по формуле
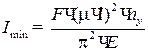
7. Если гибкость стержня l 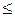
8. Вычисляют действующее напряжение s = 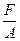
9. Вычисляют допускаемое напряжение [sу] = j и ∙[sс].
10. Сравнивают действующее напряжение с допускаемым, вычисляя относительную разницу k: k = 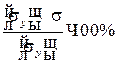
11. Если k > 0, то имеем недонапряжение, если k 5%, то в качестве второго приближения берут
j2 = j + j и и повторяют расчет, пока не будет выполняться условие |k| £ 5%.
Подбор сечения по изложенному алгоритму представлен в виде
В сопротивлении стержней продольному изгибу основную роль
играет гибкость стержня и, следовательно, величина наименьшего радиуса инерции сечения, поэтому существенным является вопрос не только величины площади сечения, как при расчете на прочность, но и формы поперечного сечения.
Для наиболее оптимального выбора сечения необходимо
конструировать сечение так, чтобы при определенной площади
величина наименьшего радиуса инерции была бы возможно большей. Для этого прежде всего следует стремиться к тому, чтобы центральные моменты инерции сечения были равны. Такой стержень будет оказывать одинаковое сопротивление потере устойчивости в любом направлении.
Далее, необходимо стремиться к получению при данной площади
наибольших центральных моментов инерции. Для этого надо разместить материал сечения по возможности дальше от центра тяжести. Этим условиям хорошо удовлетворяют трубчатое сечение или сечение, составленное из двух швеллеров, раздвинутых на определенное расстояние.
На выбор материала для сжатых стержней влияют два фактора: