в чем заключается тригонометрическое нивелирование
Тригонометрическое нивелирование



Тригонометрическое нивелирование – определение высот точек земной поверхности относительно исходной точки с помощью угла наклона визирного луча, проходящего через две точки местности,
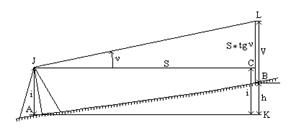
Выполняют тригонометрическое нивелирование с помощью теодолита в точке А угол наклона n визирного луча, проходящего через визирную цель в точке В, и зная горизонтальное расстояние s между этими точками, высоту инструмента l и высоту цели а (рис. 2), разность высот h этих точек вычисляют по формуле:
Эта формула точна только для малых расстояний, когда можно не считаться с влиянием кривизны Земли и искривлением светового луча в атмосфере (см. Рефракция).
Более полная формула имеет вид:
где R – радиус Земли как шара и k – коэффициент рефракции.
Тригонометрическим нивелирование определяют высоты пунктов триангуляции и полигонометрии. Оно широко применяется в топографической съёмке. Тригонометрическое нивелирование позволяет определять разности высот двух значительно удалённых друг от друга пунктов, между которыми имеется оптическая видимость, но менее точно, чем геометрическое нивелирование Точность его результатов в основном зависит от трудно учитываемого влияния земной рефракции.
Высотные и плановые геодезические сети
Геодезические измерения могут производиться не только в горизонтальной плоскости, но и в вертикальной. Нельзя точно сказать, какой тип изысканий является наиболее востребованным, так как геодезия активно используется и для исследования нетронутых цивилизацией просторов и для измерений сложных инженерно-технических конструкций.
В зависимости от положения пунктов сетей они подразделяются на три группы:
| Плановые сети | Представляют собой совокупность пунктов, которые имеют исключительно горизонтальные координаты. Выполняются на плоскости, не требующей дополнительного нивелирования контрольных точек. Используются для составления кадастрового плана земельного участка и межевания территории. |
| Высотные сети | Используются для геодезической съемки фасадов зданий, а также любых рукотворных и нерукотворных объектов, имеющих множество контрольных точек с разной высотой. |
| Планово-высотные сети | Комбинируют оба способа измерений и потому представляются наиболее сложными и трудоемкими. Построение планово-высотных сетей востребовано в промышленности. |
Вне зависимости от пространственного положения пунктов той или иной сети они объединяются вместе тремя способами – триангуляцией, трилатерацией или полигонометрией. Каждый из них может применяться для измерения любых объектов, так как основой всех расчетов является расстояние между контрольными точками (пунктами) и углы, образуемые вымышленными линиями, проложенными между ними.
Поскольку форма и размеры измеряемых объектов значения не имеют, геодезическая съемка фасадов применяется по отношению к любым зданиям. То же можно сказать и о горизонтальных измерениях. Кадастровый план земельного участка составляется без учета его формы и рельефа, а это значит, что измерения должны быть проведены в любом случае.
Настоящие профессионалы в области геодезических исследований смогут обеспечить высокую точность измерений, всегда выполняя свою работу грамотно и качественно. Построение геодезических сетей возможно на любых поверхностях, уровень сложности зависит только от квалификации привлеченных специалистов. В работе мы используем современное лазерное оборудование. Возникла потребность в геодезических изысканиях? Звоните в НПО «ГеоФонд»!
Метод тригонометрического нивелирования



LC + CK = LB + BK и S * tg( ν) + i = V + h.
Отсюда выразим превышение h
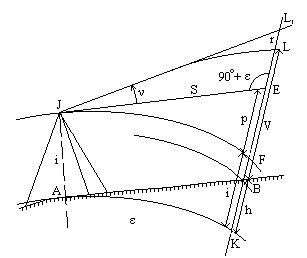
Выведем формулу превышения из тригонометрического нивелирования с учетом кривизны Земли и рефракции. Вследствие рефракции луч от верхнего конца вехи идет по кривой, а визирная линия трубы будет направлена по касательной к этой кривой в точке J. Визирная линия трубы пересечет продолжение вехи в точке L1, а не L. Проведем уровенные поверхности в точках A, B, J (рис.4.39).
Превышение точки B относительно A выражается отрезком BK. Отрезок L1K на рис.4.39 можно выразить через его части двумя путями:
Отрезок L1E найдем из Δ JL1E. Этот треугольник можно считать прямоугольным, так как угол L1EJ очень мало отличается от прямого, всего лишь на величину центрального угла ε =(S / R)*r. Этот угол при S = 1 км не превосходит 0.5′.
но поскольку JE = S, то L1E = S * tg(ν).
Отрезок EF выражает влияние кривизны Земли:
отрезок FK равен высоте прибора FK = i; отрезок L1L выражает влияние рефракции:
L1L = r * (S 2 / 2*R) * k = p * k;
отрезок LB равен высоте вехи V.
S * tg(ν) + p + i = r + V + h,
При измерении расстояния с помощью нитяного дальномера формула превышения несколько изменяется; так как S = (Cl + c)* Cos 2 (ν), то
Величину h’= 0.5*(Cl + c)*Sin(2*ν) называют тахеометрическим превышением.
При S = 100 м величиной f можно пренебречь, так как
Ошибка измерения превышения из тригонометрического нивелирования оценивается величиной от 2 см до 10 см на 100 м расстояния.
При последовательном измерении превышений получается высотный ход; в высотном ходе углы наклона измеряют дважды: в прямом и обратном направлениях.
Основы геодезии
О геодезии и разный полезный материал для геодезистов.
Понятие о тригонометрическом нивелировании
LC + CK = LB + BK и S * tg( ν) + i = V + h.
Отсюда выразим превышение h
h = S * tg(ν) + i – V. (4.67)
Выведем формулу превышения из тригонометрического нивелирования с учетом кривизны Земли и рефракции. Вследствие рефракции луч от верхнего конца вехи идет по кривой, а визирная линия трубы будет направлена по касательной к этой кривой в точке J. Визирная линия трубы пересечет продолжение вехи в точке L1, а не L. Проведем уровенные поверхности в точках A, B, J (рис.4.39).
Проведем касательную к уровенной поверхности в точке J и обозначим: высоту прибора – i, высоту вехи – V, горизонтальное проложение линии AB – S.
Превышение точки B относительно A выражается отрезком BK. Отрезок L1K на рис.4.39 можно выразить через его части двумя путями:
L1K = L1E + EF + FK,
L1K = L1L + LB + BK.
Отрезок L1E найдем из Δ JL1E. Этот треугольник можно считать прямоугольным, так как угол L1EJ очень мало отличается от прямого, всего лишь на величину центрального угла ε =(S / R)*r. Этот угол при S = 1 км не превосходит 0.5′.
но поскольку JE = S, то L1E = S * tg(ν).
Отрезок EF выражает влияние кривизны Земли:
отрезок FK равен высоте прибора FK = i; отрезок L1L выражает влияние рефракции:
L1L = r * (S2 / 2*R) * k = p * k;
отрезок LB равен высоте вехи V.
S * tg(ν) + p + i = r + V + h,
h = S * tg(ν) + (i – V) + (p – r),
h = S * tg(ν) + (i – V) + f. (4.68)
При измерении расстояния с помощью нитяного дальномера формула превышения несколько изменяется; так как S = (Cl + c)* Cs2(ν), то
h = 0.5*(Cl + c)*Sin(2*ν) + i – V + f = h’+ i – V + f,
Величину h’= 0.5*(Cl + c)*Sin(2*ν) называют тахеометрическим превышением.
При S = 100 м величиной f можно пренебречь, так как
где S – расстояние (в сотнях метров).
Ошибка измерения превышения из тригонометрического нивелирования оценивается величиной от 2 см до 10 см на 100 м расстояния.
При последовательном измерении превышений получается высотный ход; в высотном ходе углы наклона измеряют дважды: в прямом и обратном направлениях.