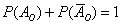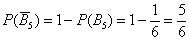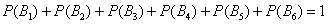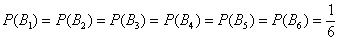в чем заключается теория вероятности
Теория вероятности: формулы и примеры решения задач
«Случайности не случайны». Звучит так, словно сказал философ, но на деле изучать случайности удел великой науки математики. В математике случайностями занимается теория вероятности. Формулы и примеры заданий, а также основные определения этой науки будут представлены в статье.
Что такое теория вероятности?
Теория вероятности – это одна из математических дисциплин, которая изучает случайные события.
Чтобы было немного понятнее, приведем небольшой пример: если подкинуть вверх монету, она может упасть «орлом» или «решкой». Пока монета находится в воздухе, обе эти вероятности возможны. То есть вероятность возможных последствий соотносится 1:1. Если из колоды с 36-ю картами вытащить одну, тогда вероятность будет обозначаться как 1:36. Казалось бы, что здесь нечего исследовать и предугадывать, тем более при помощи математических формул. Тем не менее, если повторять определенное действие много раз, то можно выявить некую закономерность и на ее основе спрогнозировать исход событий в других условиях.
Если обобщить все вышесказанное, теория вероятности в классическом понимании изучает возможность возникновения одного из возможных событий в числовом значении.
Со страниц истории
Теория вероятности, формулы и примеры первых заданий появились еще в далеком Средневековье, когда впервые возникли попытки спрогнозировать исход карточных игр.
Изначально теория вероятности не имела ничего общего с математикой. Она обосновывалась эмпирическими фактами или свойствами события, которое можно было воспроизвести на практике. Первые работы в этой сфере как в математической дисциплине появились в XVII веке. Родоначальниками стали Блез Паскаль и Пьер Ферма. Длительное время они изучали азартные игры и увидели определенные закономерности, о которых и решили рассказать обществу.
Такую же методику изобрел Христиан Гюйгенс, хотя он не был знаком с результатами исследований Паскаля и Ферма. Понятие «теория вероятности», формулы и примеры, что считаются первыми в истории дисциплины, были введены именно им.
Немаловажное значение имеют и работы Якоба Бернулли, теоремы Лапласа и Пуассона. Они сделали теорию вероятности больше похожей на математическую дисциплину. Свой теперешний вид теория вероятностей, формулы и примеры основных заданий получили благодаря аксиомам Колмогорова. В результате всех изменений теория вероятности стала одним из математических разделов.
Базовые понятия теории вероятностей. События
Главным понятием этой дисциплины является «событие». События бывают трех видов:
Все события в примерах обозначаются заглавными латинскими буквами, за исключением Р, которой отведена другая роль. Например:
В практических заданиях события принято записывать словами.
Еще события бывают совместимыми и несовместимыми. Совместимые события не исключают появления друг друга. Например:
Эти события независимы друг от друга, и появление одного из них не влияет на появление другого. Несовместимые события определяются тем, что появление одного исключает появление другого. Если говорить о той же монете, то выпадение «решки» делает невозможным появление «орла» в этом же эксперименте.
Действия над событиями
События можно умножать и складывать, соответственно, в дисциплине вводятся логические связки «И» и «ИЛИ».
Сумма определяется тем, что может появиться или событие А, или В, или два одновременно. В случае когда они несовместимы, последний вариант невозможен, выпадет или А, или В.
Умножение событий заключается в появлении А и В одновременно.
Теперь можно привести несколько примеров, чтобы лучше запомнились основы, теория вероятности и формулы. Примеры решения задач далее.
Задание 1: Фирма принимает участие в конкурсе на получение контрактов на три разновидности работы. Возможные события, которые могут произойти:
С помощью действий над событиями попробуем выразить следующие ситуации:
В математическом виде уравнение будет иметь следующий вид: К = АВС.
Усложняем задание: H = «фирма получит один контракт». Поскольку не известно, какой именно контракт получит фирма (первый, второй или третий), необходимо записать весь ряд возможных событий:
А1ВС1 – это ряд событий, где фирма не получает первый и третий контракт, но получает второй. Соответственным методом записаны и другие возможные события. Символ υ в дисциплине обозначает связку «ИЛИ». Если перевести приведенный пример на человеческий язык, то фирма получит или третий контракт, или второй, или первый. Подобным образом можно записывать и другие условия в дисциплине «Теория вероятности». Формулы и примеры решения задач, представленные выше, помогут сделать это самостоятельно.
Собственно, вероятность
Пожалуй, в этой математической дисциплине вероятность события – это центральное понятие. Существует 3 определения вероятности:
Каждое имеет свое место в изучении вероятностей. Теория вероятности, формулы и примеры (9 класс) в основном используют классическое определение, которое звучит так:
Формула выглядит так: Р(А)=m/n.
А – собственно, событие. Если появляется случай, противоположный А, его можно записывать как Ā или А1.
m – количество возможных благоприятных случаев.
n – все события, которые могут произойти.
Например, А = «вытащить карту червовой масти». В стандартной колоде 36 карт, 9 из них червовой масти. Соответственно, формула решения задания будет иметь вид:
В итоге вероятность того, что из колоды вытянут карту червовой масти, составит 0,25.
К высшей математике
Теперь стало немного известно, что такое теория вероятности, формулы и примеры решения заданий, которые попадаются в школьной программе. Однако теория вероятностей встречается и в высшей математике, которая преподается в вузах. Чаще всего там оперируют геометрическими и статистическими определениями теории и сложными формулами.
Статистический подход не противоречит классическому, а немного расширяет его. Если в первом случае нужно было определить, с какой долей вероятности произойдет событие, то в этом методе необходимо указать, как часто оно будет происходить. Здесь вводится новое понятие «относительная частота», которую можно обозначить Wn(A). Формула ничем не отличается от классической:
Если классическая формула вычисляется для прогнозирования, то статистическая – согласно результатам эксперимента. Возьмем, к примеру, небольшое задание.
Отдел технологического контроля проверяет изделия на качество. Среди 100 изделий нашли 3 некачественных. Как найти вероятность частоты качественного товара?
А = «появление качественного товара».
Таким образом, частота качественного товара составляет 0,97. Откуда взяли 97? Из 100 товаров, которые проверили, 3 оказались некачественными. От 100 отнимаем 3, получаем 97, это количество качественного товара.
Немного о комбинаторике
Например, из города А в город В ведет 5 дорог. Из города В в город С ведет 4 пути. Сколькими способами можно доехать из города А в город С?
Все просто: 5х4=20, то есть двадцатью разными способами можно добраться из точки А в точку С.
Усложним задание. Сколько существует способов раскладывания карт в пасьянсе? В колоде 36 карт – это исходная точка. Чтобы узнать количество способов, нужно от исходной точки «отнимать» по одной карте и умножать.
То есть 36х35х34х33х32…х2х1= результат не вмещается на экран калькулятора, поэтому его можно просто обозначить 36!. Знак «!» возле числа указывает на то, что весь ряд чисел перемножается между собой.
В комбинаторике присутствуют такие понятия, как перестановка, размещение и сочетание. Каждое из них имеет свою формулу.
Соединения из n элементов, которые отличаются только порядком размещения, называют перестановкой. В математике это имеет вид: Рn = n!
Сочетаниями из n элементов по m называют такие соединения, в которых важно, какие это были элементы и каково их общее количество. Формула будет иметь вид:
Формула Бернулли
Вероятность (р) появления события (А) неизменна для каждого испытания. Вероятность того, что ситуация произойдет ровно m раз в n количестве экспериментов, будет вычисляться формулой, что представлена выше. Соответственно, возникает вопрос о том, как узнать число q.
Если событие А наступает р количество раз, соответственно, оно может и не наступить. Единица – это число, которым принято обозначать все исходы ситуации в дисциплине. Поэтому q – число, которое обозначает возможность ненаступления события.
Теперь вам известна формула Бернулли (теория вероятности). Примеры решения задач (первый уровень) рассмотрим далее.
Задание 2: Посетитель магазина сделает покупку с вероятностью 0,2. В магазин зашли независимым образом 6 посетителей. Какова вероятность того, что посетитель сделает покупку?
Решение: Поскольку неизвестно, сколько посетителей должны сделать покупку, один или все шесть, необходимо просчитать все возможные вероятности, пользуясь формулой Бернулли.
А = «посетитель совершит покупку».
В этом случае: р = 0,2 (как указано в задании). Соответственно, q=1-0,2 = 0,8.
n = 6 (поскольку в магазине 6 посетителей). Число m будет меняться от 0 (ни один покупатель не совершит покупку) до 6 (все посетители магазина что-то приобретут). В итоге получим решение:
P6(0) = C0 6 ×p 0 ×q 6 =q 6 = (0,8) 6 = 0,2621.
Ни один из покупателей не совершит покупку с вероятностью 0,2621.
Как еще используется формула Бернулли (теория вероятности)? Примеры решения задач (второй уровень) далее.
После вышеприведенного примера возникают вопросы о том, куда делись С и р. Относительно р число в степени 0 будет равно единице. Что касается С, то его можно найти формулой:
Поскольку в первом примере m = 0, соответственно, С=1, что в принципе не влияет на результат. Используя новую формулу, попробуем узнать, какова вероятность покупки товаров двумя посетителями.
P6(2) = C6 2 ×p 2 ×q 4 = (6×5×4×3×2×1) / (2×1×4×3×2×1) × (0,2) 2 × (0,8) 4 = 15 × 0,04 × 0,4096 = 0,246.
Не так уж и сложна теория вероятности. Формула Бернулли, примеры которой представлены выше, прямое тому доказательство.
Формула Пуассона
Уравнение Пуассона используется для вычисления маловероятных случайных ситуаций.
При этом λ = n х p. Вот такая несложная формула Пуассона (теория вероятности). Примеры решения задач рассмотрим далее.
Задание 3: На заводе изготовили детали в количестве 100000 штук. Появление бракованной детали = 0,0001. Какова вероятность, что в партии будет 5 бракованных деталей?
А = «случайно выбранная деталь будет бракованной».
р = 0,0001 (согласно условию задания).
n = 100000 (количество деталей).
m = 5 (бракованные детали). Подставляем данные в формулу и получаем:
Так же как и формула Бернулли (теория вероятности), примеры решений с помощью которой написаны выше, уравнение Пуассона имеет неизвестное е. По сути его можно найти формулой:
Однако есть специальные таблицы, в которых находятся практически все значения е.
Теорема Муавра-Лапласа
Если в схеме Бернулли количество испытаний достаточно велико, а вероятность появления события А во всех схемах одинакова, то вероятность появления события А определенное количество раз в серии испытаний можно найти формулой Лапласа:
Чтобы лучше запомнилась формула Лапласа (теория вероятности), примеры задач в помощь ниже.
Задание 4: Рекламный агент раздает 800 листовок. Согласно статистическим исследованиям, каждая третья листовка находит своего потребителя. Какова вероятность того, что сработает ровно 267 рекламных листовок?
Сначала найдем Xm, подставляем данные (они все указаны выше) в формулу и получим 0,025. При помощи таблиц находим число ϕ(0,025), значение которого 0,3988. Теперь можно подставлять все данные в формулу:
Р800(267) = 1/√(800 х 1/3 х 2/3) х 0,3988 = 3/40 х 0,3988 = 0,03.
Таким образом, вероятность того, что рекламная листовка сработает ровно 267 раз, составляет 0,03.
Формула Байеса
Формула Байеса (теория вероятности), примеры решения заданий с помощью которой будут приведены ниже, представляет собой уравнение, которое описывает вероятность события, опираясь на обстоятельства, которые могли быть связаны с ним. Основная формула имеет следующий вид:
Р (А|B) = Р (В|А) х Р (А) / Р (В).
А и В являются определенными событиями.
Р(А|B) – условная вероятность, то есть может произойти событие А при условии, что событие В истинно.
Р (В|А) – условная вероятность события В.
Задание 5: На склад привезли телефоны от трех компаний. При этом часть телефонов, которые изготавливаются на первом заводе, составляет 25%, на втором – 60%, на третьем – 15%. Известно также, что средний процент бракованных изделий у первой фабрики составляет 2%, у второй – 4%, и у третьей – 1%. Необходимо найти вероятность того, что случайно выбранный телефон окажется бракованным.
А = «случайно взятый телефон».
В1 – телефон, который изготовила первая фабрика. Соответственно, появятся вводные В2 и В3 (для второй и третьей фабрик).
Р (В1) = 25%/100% = 0,25; Р(В2) = 0,6; Р (В3) = 0,15 – таким образом мы нашли вероятность каждого варианта.
Теперь нужно найти условные вероятности искомого события, то есть вероятность бракованной продукции в фирмах:
Теперь подставим данные в формулу Байеса и получим:
Р (А) = 0,25 х 0,2 + 0,6 х 0,4 + 0,15 х 0,01= 0,0305.
В статье представлена теория вероятности, формулы и примеры решения задач, но это только вершина айсберга обширной дисциплины. И после всего написанного логично будет задаться вопросом о том, нужна ли теория вероятности в жизни. Простому человеку сложно ответить, лучше спросить об этом у того, кто с ее помощью не единожды срывал джек-пот.
Теория вероятностей. Базовые термины и понятия
Под занавес продолжительных летних каникул пришло время потихоньку возвращаться к высшей математике и торжественно открыть пустой вёрдовский файл, чтобы приступить к созданию нового раздела – Теория вероятностей и математическая статистика. Признаюсь, нелегко даются первые строчки, но первый шаг – это пол пути, поэтому я предлагаю всем внимательно проштудировать вводную статью, после чего осваивать тему будет в 2 раза проще! Ничуть не преувеличиваю. …Накануне очередного 1 сентября вспоминается первый класс и букварь…. Буквы складываются в слоги, слоги в слова, слова в короткие предложения – Мама мыла раму. Совладать с тервером и математической статистикой так же просто, как научиться читать! Однако для этого необходимо знать ключевые термины, понятия и обозначения, а также некоторые специфические правила, которым и посвящён данный урок.
Но сначала примите мои поздравления с началом (продолжением, завершением, нужное отметить) учебного года и примите подарок. Лучший подарок – это книга, и для самостоятельной работы я рекомендую следующую литературу:
1) Гмурман В.Е. Теория вероятностей и математическая статистика
Легендарное учебное пособие, выдержавшее более десяти переизданий. Отличается доходчивостью и предельной простой изложения материала, а первые главы так и вовсе доступны, думаю, уже для учащихся 6-7-х классов.
2) Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике
Решебник того же Владимира Ефимовича с подробно разобранными примерами и задачами.
ОБЯЗАТЕЛЬНО закачайте обе книги из Интернета или раздобудьте их бумажные оригиналы! Подойдёт и версия 60-70-х годов, что даже лучше для чайников. Хотя фраза «теория вероятностей для чайников» звучит довольно нелепо, поскольку почти всё ограничивается элементарными арифметическими действиями. Проскакивают, правда, местами производные и интегралы, но это только местами.
Я постараюсь достичь той же ясности изложения, но должен предупредить, что мой курс ориентирован на решение задач и теоретические выкладки сведены к минимуму. Таким образом, если вам нужна развёрнутая теория, доказательства теорем (да-да, теорем!), пожалуйста, обратитесь к учебнику.
Для тех, кто хочет научиться решать задачи в считанные дни, создан ускоренный курс в pdf-формате (по материалам сайта). Ну и прямо сейчас, не откладывая дело в долгую папку, мы приступаем к изучению тервера и матстата – следуйте за мной!
Рекомендуемый порядок изучения темы:
По мере прочтения статей полезно знакомиться (хотя бы бегло) с дополнительными задачами рассмотренных видов. На странице Готовые решения по высшей математике размещены соответствующие pdf-ки с примерами решений. Также заметную помощь окажут ИДЗ 18.1-18.2 Рябушко (попроще) и прорешанные ИДЗ по сборнику Чудесенко (посложнее).
Итак, дорожные указатели расставлены, и мы ступаем на тропу теории вероятностей, которую неоднократно просили осветить посетители сайта.
Первое и очень важное. Что изучает эта наука? Многим в голову наверняка пришли мысли вроде «вероятность дождя велика», «вероятность выигрыша в лотерею мала», «орёл и решка выпадают с вероятностью 50 на 50» и т.п. Но тогда сразу возникает вопрос, при чём здесь наука? Пожалуйста, прямо сейчас возьмите в руки монету и скажите, какой гранью она выпадет после броска? …Совсем не похоже на теорию – скорее какое-то гадание….
И действительно, обывательское понимание вероятности больше смахивает на некое предсказание, часто с изрядной долей мистицизма и суеверий. Теория же вероятностей изучает вероятностные закономерности массовых однородных случайных событий. То есть, у неё нет цели что-либо угадать, например, результат броска той же монеты в единичном эксперименте. Однако если одну и ту же монету в одинаковых условиях подбрасывать сотни и тысячи раз, то будет прослеживаться чёткая закономерность, описываемая вполне жёсткими законами.
Другой пример. Вокруг каждого из нас летают молекулы воздуха. Некоторые из них обладают высокой, некоторые средней, а некоторые – низкой скоростью. Не имеет смысла угадывать скорость отдельно взятых молекул; но их массовый учёт находит самое широкое применение в теоретических и прикладных физических исследованиях. Обратите внимание, что самолёты «умеют» летать, газовые и паровые котлы обычно не взрываются, а чайники при кипении не скачут по кухне. За многими и многими, казалось бы, обыденными фактами и событиями кроются серьёзные вероятностно-статистические расчёты.
Или пример попроще. Если вы приобретёте лотерейный билет, то вряд ли что-то выиграете и совсем невероятно, что сорвёте крупный куш. Но организатор лотереи даже при случайном розыгрыше тиража (извлечение пронумерованных шариков и т.п. либо если участники сами угадывают номера) гарантированно и с высокой точностью знает, сколько билетов выиграют/проиграют, и, понятно, остаётся в прибыли. Лотереи часто называют обманом, однако парадокс состоит в том, что эта гарантия строго обоснована теорией; рАвно, как и житейская фраза «всё равно ничего не выиграю». Думаю, теперь все поняли правильный способ заработка на лотереях =) Впрочем, мы ещё вернёмся к «секретам» выигрыша в рулетку и различные лотереи.
Да, кстати подумайте ещё над одной насущной задачей: многие из нас за жизнь сдают десятки экзаменов, и практически всегда имеет место следующая ситуация: часть вопросов студент знает (либо заготовлены шпоры), а часть вопросов – не знает (либо плавает как мастер спорта). Наступает день «X»: утро, коридор с 10-15 однокурсниками и дверь, за которой на столе лежит полный комплект билетов. В каком случае вероятнее сдать экзамен – если идти «в первых рядах», «в серединке» или если зайти в аудиторию в числе последних? …Изучаем теорию вероятностей!
Сначала разбираемся с основными терминами, которые ниже по тексту я буду выделять жирным курсивом. Обращаю ваше внимание, что это ИМЕННО ТЕРМИНЫ, а не «просто слова»!
События. Виды событий
Одно из базовых понятий тервера уже озвучено выше – это событие. События бывают достоверными, невозможными и случайными.
Достоверным называют событие, которое в результате испытания (осуществления определенных действий, определённого комплекса условий) обязательно произойдёт. Например, в условиях земного тяготения подброшенная монета непременно упадёт вниз.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания. Пример невозможного события: в условиях земного тяготения подброшенная монета улетит вверх.
И, наконец, событие называется случайным, если в результате испытания оно может, как произойти, так и не произойти, при этом должен иметь место принципиальный критерий случайности: случайное событие – есть следствие случайных факторов, воздействие которых предугадать невозможно или крайне затруднительно. Пример: в результате броска монеты выпадет «орёл». В рассмотренном случае случайные факторы – это форма и физические характеристики монеты, сила/направление броска, сопротивление воздуха и т.д.
Подчёркнутый критерий случайности очень важен – так, например, карточный шулер может очень ловко имитировать случайность и давать выигрывать жертве, но ни о каких случайных факторах, влияющих на итоговый результат, речи не идёт.
Любой результат испытания называется исходом, который, собственно и представляет собой появление определённого события. В частности, при подбрасывании монеты возможно 2 исхода (случайных события): выпадет орёл, выпадет решка. Естественно, подразумевается, что данное испытание проводится в таких условиях, что монета не может встать на ребро или, скажем, зависнуть в невесомости.
События (любые) обозначают большими латинскими буквами 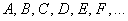
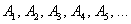
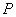
Запишем следующие случайные события:
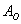
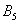
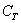
Да, события прямо так и записывают в практических задачах, при этом в уместных случаях удобно использовать «говорящие» подстрочные индексы (хотя можно обойтись и без них).
Следует в третий раз подчеркнуть, что случайные события обязательно удовлетворяют вышеприведённому критерию случайности. В этом смысле снова показателен 3-й пример: если из колоды изначально удалить все карты трефовой масти, то событие 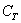
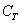
Таким образом, при розыгрыше важного жребия всегда есть смысл невзначай посмотреть, а не одинаковы ли грани монеты 😉
Другая важная характеристика событий – это их равновозможность. Два или бОльшее количество событий называют равновозможными, если ни одно из них не является более возможным, чем другие. Например:
выпадение орла или решки при броске монеты;
выпадение 1, 2, 3, 4, 5 или 6 очков при броске игрального кубика;
извлечение карты трефовой, пиковой, бубновой или червовой масти из колоды.
При этом предполагается, что монета и кубик однородны и имеют геометрически правильную форму, а колода хорошо перемешана и «идеальна» с точки зрения неразличимости рубашек карт.
Могут ли быть те же события не равновозможными? Могут! Например, если у монеты или кубика смещён центр тяжести, то гораздо чаще будут выпадать вполне определённые грани. Как говорится, ещё одна лазейка для мошенников. События 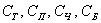
Тем не менее, в рассмотренных трёх случаях при потере равновозможности всё же сохраняется случайность событий.
Совместные и несовместные события. Противоположные события.
Полная группа событий
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой вверху. Например:
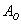
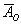
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
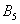
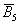
Либо пять, либо не пять – третьего не дано, т.е. события несовместны и противоположны.
Аналогично – или трефа или карта другой масти:
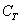
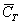
Множество несовместных событий образуют полную группу событий, если в результате отдельно взятого испытания обязательно появится одно из этих событий. Очевидно, что любая пара противоположных событий (в частности, примеры выше) образует полную группу. Однако в различных задачах с одним и тем же объектом могут фигурировать разные события, например, для игрального кубика характерно рассмотрение следующего набора:
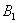
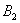
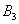
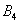
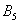
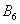
События 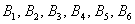
Ещё одно важное понятие, которое нам скоро потребуется – это элементарность исхода (события). Если совсем просто, то элементарное событие «нельзя разложить на другие события». Например, события 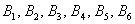
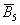
В примере с картами события 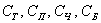
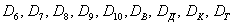
Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и, разумеется, 36 несовместных элементарных исходов тоже образуют полную группу событий.
Совместные события менее значимы с точки зрения решения практических задач, но обходить их стороной не будем. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого. Например:
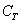
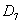
Если быть совсем лаконичным, одно не исключает другого.
Понятие совместности охватывает и бОльшее количество событий:
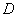
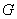
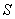
Ситуация, конечно, довольно редкая, но совместное появление всех трёх событий в принципе не исключено. Следует отметить, что перечисленные события совместны и попарно, т.е. может быть только ливень с грозой или грибной дождик, или погромыхает неподалёку на фоне ясного неба.
Алгебра событий
Мужайтесь, будет и матан =)
Пожалуйста, запомните ВАЖНЕЙШЕЕ ПРАВИЛО, без которого освоить тервер просто нереально:
Операция сложения событий означает логическую связку ИЛИ,
а операция умножения событий – логическую связку И.
1) Суммой двух событий 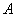
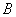
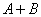
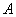
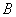
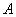
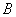
Правило распространяется и на бОльшее количество слагаемых, например, событие 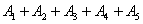
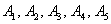
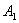
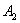
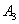
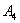
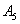
События 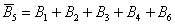
Событие 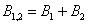
Событие 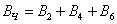
Событие 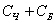
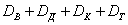
Чуть занятнее дело с совместными событиями:
Событие 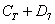
Событие 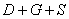
– или будет только дождь / только гроза / только солнце;
– или наступит только какая-нибудь пара событий (дождь + гроза / дождь + солнце / гроза + солнце);
– или все три события появятся одновременно.
То есть, событие 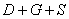
Второй столп алгебры событий:
2) Произведением двух событий 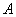
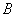
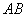
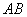
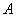
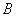
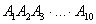
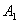
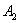
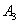
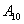
Рассмотрим испытание, в котором подбрасываются две монеты и следующие события:
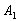
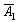
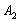
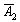
Тогда:
– событие 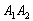
– событие 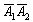
– событие 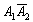
– событие 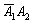
Нетрудно заметить, что события 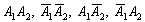
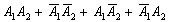
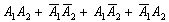
Это был пример, когда в одном испытании задействовано несколько объектов, в данном случае – две монеты. Другая распространенная в практических задачах схема – это повторные испытания, когда, например, один и тот же игральный кубик бросается 3 раза подряд. В качестве демонстрации рассмотрим следующие события:
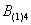
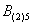
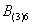
Тогда событие 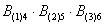
…Понимаю, что, возможно, разбираются не очень интересные примеры, но это часто встречающиеся в задачах вещи и от них никуда не деться. Помимо монетки, кубика и колоды карт вас поджидают урны с разноцветными шарами, несколько анонимов, стреляющих по мишени, и неутомимый рабочий, который постоянно вытачивает какие-то детали =)
Вероятность события
Вероятность события – это центральное понятие теории вероятностей. …Убийственно логичная вещь, но с чего-то надо было начинать =) Существует несколько подходов к её определению:
В данной статье я остановлюсь на классическом определении вероятностей, которое находит наиболее широкое применение в учебных заданиях.
Обозначения. Вероятность некоторого события 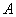
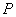
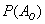
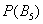
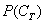
Также для обозначения вероятности широко используется маленькая буква 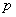
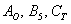
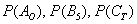
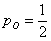
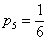
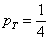
Данный вариант популярен при решении практических задач, поскольку позволяет заметно сократить запись решения. Как и в первом случае, здесь удобно использовать «говорящие» подстрочные/надстрочные индексы.
Все уже давно догадались о числах, которые я только что записал выше, и сейчас мы узнаем, как они получились:
Классическое определение вероятности:
Вероятностью наступления события 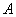
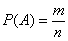
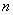
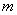
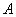
При броске монеты может выпасть либо орёл, либо решка – данные события образуют полную группу, таким образом, общее число исходов 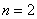
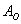
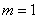
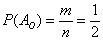
Аналогично – в результате броска кубика может появиться 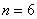
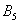
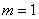
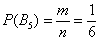
Особое внимание обращаю на третий пример. Здесь будет некорректным сказать «раз в колоде 4 масти, то вероятность извлечения трефы 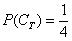
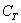
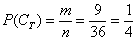
Вероятности можно выразить и в процентах, например: вероятность выпадение орла равна 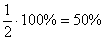
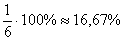
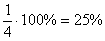
Принято использовать доли единицы, и, очевидно, что вероятность может изменяться в пределах 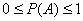
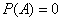
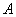
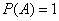
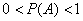
! Если в ходе решения любой задачи у вас получилось какое-то другое значение вероятности – ищите ошибку!
При классическом подходе к определению вероятности крайние значения (ноль и единица) получаются посредством точно таких же рассуждений. Пусть из некой урны, в которой находятся 10 красных шаров, наугад извлекается 1 шар. Рассмотрим следующие события:
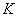
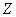
Общее количество исходов: 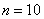
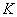
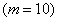
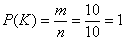
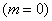
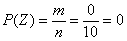
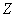
Особый интерес представляют события, вероятность наступления которых чрезвычайно мала. Хоть такие события и являются случайными, для них справедлив следующий постулат:
в единичном испытании маловозможное событие не произойдёт.
Но грустить не нужно, потому что есть противоположный принцип: если вероятность некоторого события очень близка к единице, то в отдельно взятом испытании оно практически достоверно произойдёт. Поэтому перед прыжком с парашютом не надо бояться, наоборот – улыбайтесь! Ведь должны сложиться совершенно немыслимые и фантастические обстоятельства, чтобы отказали оба парашюта.
Хотя всё это лирика, поскольку в зависимости от содержания события первый принцип может оказаться весёлым, а второй – грустным; или вообще оба параллельными.
Пожалуй, пока достаточно, на уроке Задачи на классическое определение вероятности мы выжмем максимум из формулы 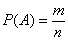
Сумма вероятностей событий, которые образуют полную группу, равна единице. Грубо говоря, если события образуют полную группу, то со 100%-й вероятностью какое-то из них произойдёт. В самом простом случае полную группу образуют противоположные события, например:
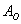
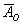
По теореме:
Совершенно понятно, что данные события равновозможны и их вероятности одинаковы 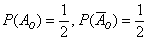
По причине равенства вероятностей равновозможные события часто называют равновероятными. А вот и скороговорка на определение степени опьянения получилась =)
Пример с кубиком: события 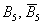
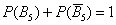
Рассматриваемая теорема удобна тем, что позволяет быстро найти вероятность противоположного события. Так, если известна вероятность 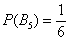
Это гораздо проще, чем суммировать вероятности пяти элементарных исходов. Для элементарных исходов, к слову, данная теорема тоже справедлива:
События 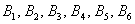
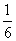
Ну и на закуску колода: поскольку нам известна вероятность 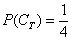
Заметьте, что рассмотренные пары событий 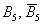
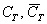
В упрощенной версии записи решения вероятность противоположного события стандартно обозначается строчной буквой 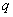
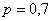
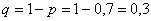
! В теории вероятностей буквы 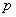
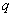
В честь Дня Знаний я не буду задавать домашнее задание =), но очень важно, чтобы вы могли ответить на следующие вопросы:
– Какие виды событий существуют?
– Что такое случайность и равновозможность события?
– Как вы понимаете термины совместность/несовместность событий?
– Что такое полная группа событий, противоположные события?
– Что означает сложение и умножение событий?
– В чём суть классического определения вероятности?
– Чем полезна теорема сложения вероятностей событий, образующих полную группу?
Нет, зубрить ничего не надо, это всего лишь азы теории вероятностей – своеобразный букварь, который довольно быстро уложится в голове. И чтобы это произошло как можно скорее, предлагаю ознакомиться с уроками Задачи по комбинаторике и Задачи на классическое определение вероятности.
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5