в чем заключается суть метода относительного движения судов

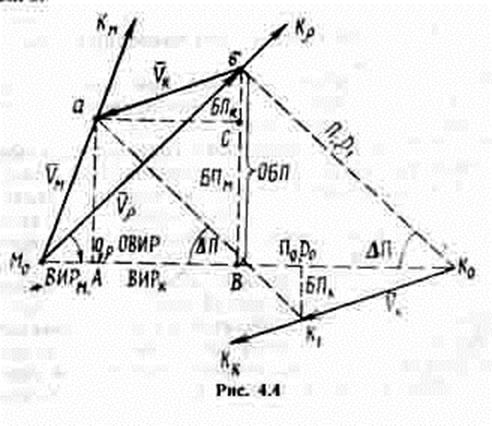
При двустороннем маневрировании скорости изменения дистанции, бокового перемещения и пеленга между кораблями определяются параметрами движения обоих кораблей. Рассуждая аналогично случаю одностороннего маневрирования, получим следующие формулы для решения задач двустороннего маневрирования (рис. 4.4):

(4.20)

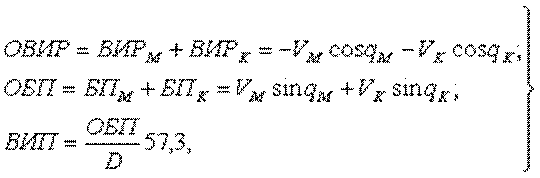
Тогда элементы позиции маневрирующего корабля при двустороннем маневрировании по истечении времени маневра можно представить в виде:

(4.21)

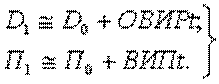
Так как, пользуясь основными элементами маневрирования, в выражениях разложения расстояния и пеленга в ряд Тейлора

(4.22)

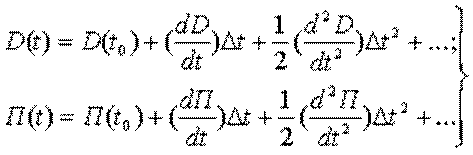
мы учитываем члены только первого порядка, тем самым допуская ошибку, которая численно будет равна остаточному члену ряда. При решении задач маневрирования по формулам (4.19) и (4.21) ошибки будут тем большими, чем больше t. В практике маневрирования допустимо решать задачи по формулам (4.19), (4.21) для промежутков времени маневрирования, равных нескольким минутам. Особенно значительными могут быть ошибки при быстром изменении пеленга, то есть при больших значениях ВИП. Для быстроты решения задач маневрирования с применением ВИР, БП и ВИП пользуются табл. 31а, МТ-75.

Элементы маневрирования можно выразить через относительное движение. Из рис. 4.4 следует:

(4.23)

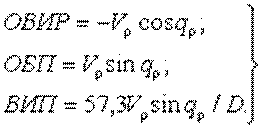
4.5 Задачи тактического маневрирования

В быстро меняющейся обстановке современного морского боя может возникнуть необходимость в кратчайший срок изменить дистанцию, с максимальной скоростью изменить пеленг на противника или, наоборот, сохранить его, изменив дистанцию, и т. д. В каждом конкретном случае необходимо правильно выбрать прием маневрирования.

Для расчета элементов маневра применяются аналитический, табличный, приборный и графический способы.

Аналитический способ заключается в определении искомых величин по формулам. Этот способ чаще применяется при исследовательских разработках, теоретических расчетах и при составлении таблиц. Для решения задач в практике маневрирования способ широкого применения не получил, так как не дает возможности решить задачу достаточно быстро и не обладает наглядностью.

Табличный способ, когда искомые величины находят по таблицам, применяется только при решении некоторых типов задач маневрирования, универсальных таблиц для решения всех задач маневрирования пока не существует. Кроме того, этот способ не обладает достаточными точностью и наглядностью, поэтому широкого распространения на кораблях для решения задач маневрирования не получил.

Широкое применение вычислительной техники, позволяющей быстро и точно определить элементы маневрирования, способствовало тому, что приборный способ стал основным для решения задач маневрирования.

Графический способ решения задач маневрирования прост и удобен. В отличие от других способов он нагляден и позволяет легко проконтролировать все решения. Этот способ обеспечивает достаточные для практических целей быстроту и точность, является наиболее универсальным и автономным. Выполнение расчетов маневрирования графически обязательно даже в том случае, когда решение задачи обеспечивается другими способами. Это дублирование вызывается требованиями живучести управления.

Графическое решение задач маневрирования может выполняться на навигационной карте, на листе бумаги или на маневренном планшете. Маневренный планшет (см. рис. 4.7) представляет собой совмещенные азимутальную и стадиметрическую сетки. Началом координат является совмещенный центр обеих сеток.

Азимутальная сетка образована рядом радиальных прямых, проведенных из центра планшета через каждые 10°. Стадиметрическая сетка служит масштабной шкалой. Она образована рядом концентрических окружностей, проведенных на одинаковом удалении одна от другой. На внешней окружности стадиметрической сетки нанесены две шкалы градусных делений от 0 до 360°.

Наружная шкала обозначает направления от центра планшета относительно линии 0-180, принятой за меридиан. Внутренняя шкала отличается от внешней на 180, поэтому она используется при нанесении (снятии) обратных пеленгов.

4.6 Предвычисление (прогнозирование) элементов относительных позиций

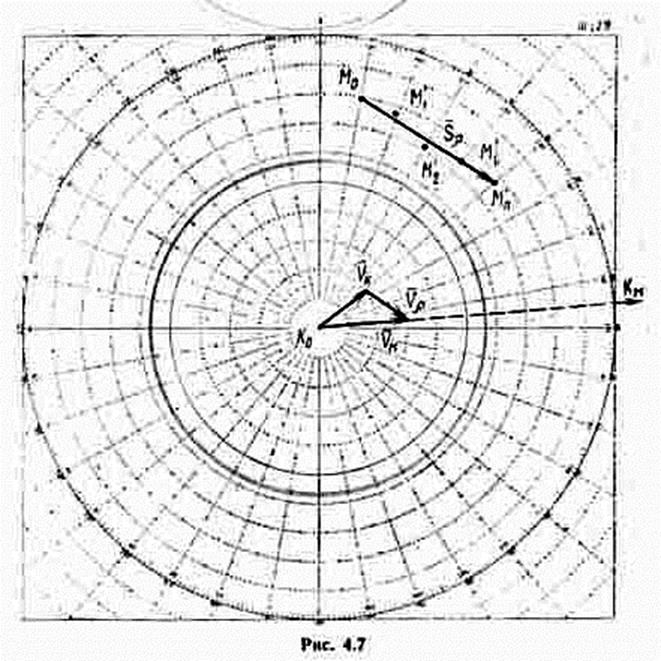
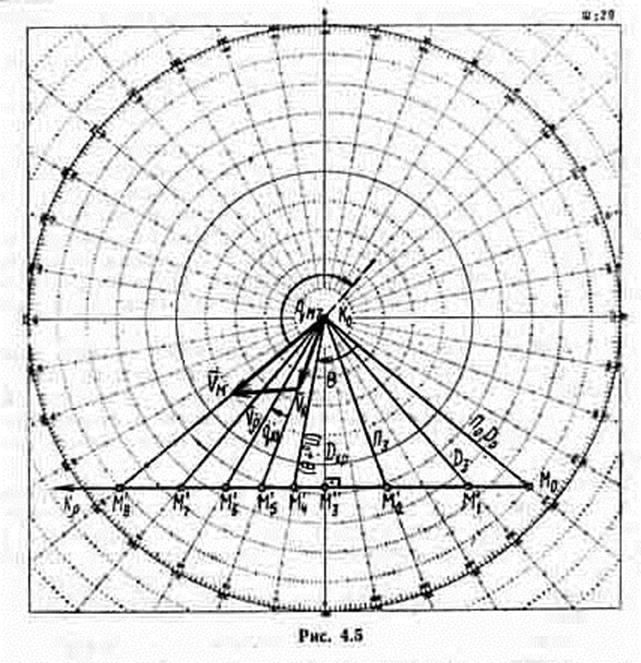
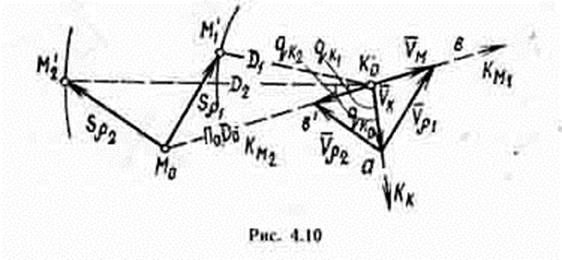
Зная элементы движения кораблей и их начальное взаимное положение, можно, построив треугольник скоростей, из позиции М₀ провести относительный курс К_r (рис. 4.5), определить (прогнозировать) взаимное положение кораблей на любой момент времени. Типовыми задачами такого рода являются:

1. Расчет позиции маневрирующего корабля, когда расстояние до объекта маневра равно заданной величине D₃.

Для решения задачи нужно раствором циркуля, равным в принятом масштабе заданной дистанции, из точки К₀ сделать засечку на линии относительного движения К_r. Полученная точка М ‘₁ соответствует заданному положению между кораблями.

2. Расчет позиции, когда пеленг на объект маневра равен заданному значению П₃.

Проведя из точки К₀ линию заданного пеленга, получим точку пересечения ее с линией относительного курса К_r, в которой находится позиция М ‘₂ соответствующая поставленному условию.

3. Определение момента, когда расстояние между кораблями кратчайшее D_кр.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

4.8 Решение задач тактического маневрирования на маневренном планшете

4.8.1 Одновременное изменение направления на объект маневра и дистанции до него

Одновременное изменение направления на объект маневра и дистанции до него является наиболее общей задачей тактического маневрирования. Большинство других задач на изменение позиции сводится к частным случаям этой общей задачи.

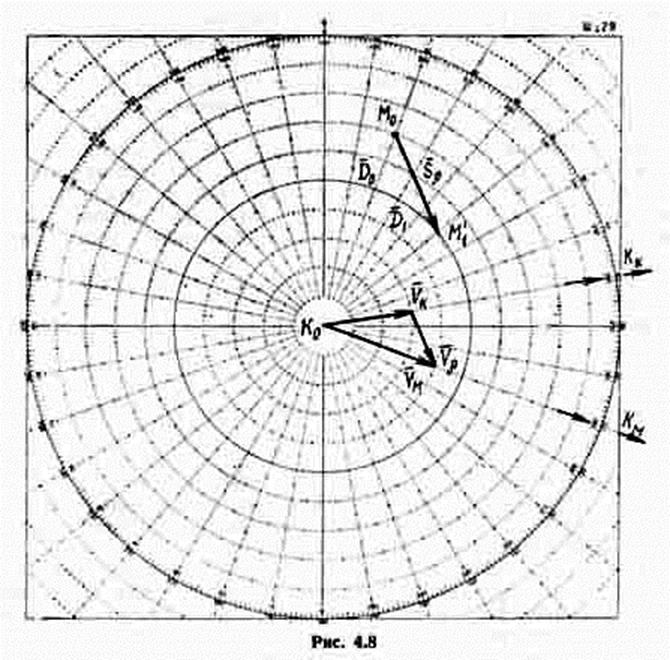
Чтобы рассчитать маневр, необходимо знать элементы движения объекта маневра К_к и V_к а также элементы позиции маневрирующего корабля П₀, D₀ на момент начала выполнения маневра. Предположим, что в заданный момент времени T₀ маневрирующий корабль находится относительно объекта маневра по пеленгу П₀ в дистанции D₀ (рис. 4.8). Объект маневра следует курсом К_к и скоростью V_к.

Чтобы найти время маневра, нужно, исходя из масштабов построений, определить величину относительного перемещения S_r, величину относительной скорости V_r и рассчитать время маневра t = S_r /V_r.

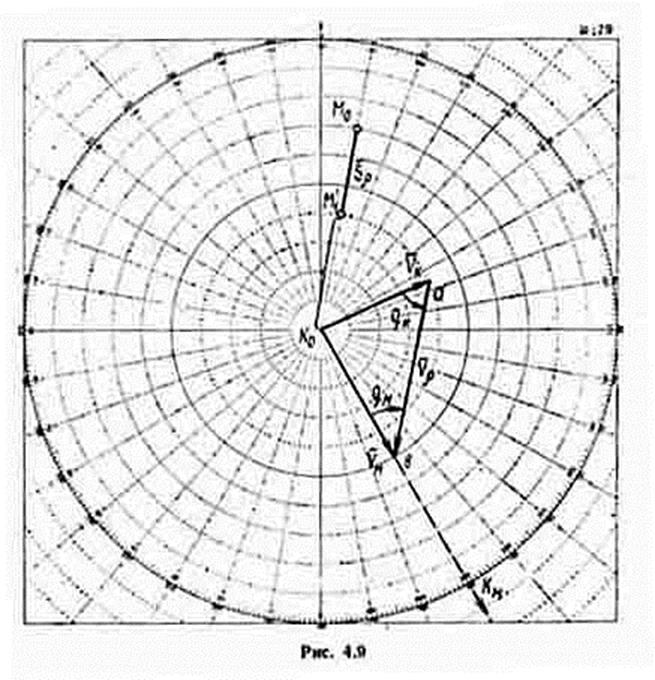
4.8.2 Изменение дистанции при постоянстве пеленга

Маневр изменения дистанции применяется в том случае, когда направление на объект маневра уже удовлетворяет поставленной задаче. Эта задача решается как частный случай рассмотренной выше задачи изменения позиции.

При построении треугольника позиций относительная позиция М ‘₁ (рис. 4.9) будет находиться на линии начального пеленга на заданной дистанции D₃ от объекта маневра, то есть линия относительного перемещения совпадает с линией начального пеленга. Поэтому треугольник позиций представляет собой прямую линию К₀М₀М ‘₁.

Из треугольника скоростей следует, что

Если при постоянстве пеленга происходит сближение кораблей, то правая и левая части (4.24) будут иметь противоположные знаки (корабли маневрируют разноименными бортами). Тогда ОБП = БП_м + БП_к = 0, то есть, сближаясь при постоянстве пеленга, корабли М и К придут в точку пересечения линий их курсов одновременно. В связи с этим, обнаружив, что пеленг на приближающийся корабль не меняется, во избежание столкновения необходимо нарушить равенство боковых перемещений изменением курса или скорости своего корабля.

Рассмотренный маневр изменения дистанции без изменения пеленга позволяет сделать следующие выводы:

— маневр изменения дистанции при постоянстве пеленга можно выполнить относительно объекта, курс и скорость которого неизвестны, для этого необходимо добиться равенства боковых перемещений;

— из выражения (4.25) вытекает возможность определения одного из элементов движения цели, когда известен другой:

Наиболее часто этот маневр применяется при выходе в атаку, особенно на малых дистанциях, когда необходимо сократить дистанцию и уточнить элементы движения цели, сохранив ее курсовой угол.

4.8.3 Изменение дистанции до цели курсом, равным или обратным начальному пеленгу на нее

При обнаружении цели на больших дистанциях, когда величина изменения пеленга мала, а элементы движения цели определить не представляется возможным, целесообразно применение маневра курсом, равным пеленгу обнаружения, для сокращения дистанции, или курсом, обратным пеленгу, для ее увеличения. Обоснование этого способа изменения дистанции вытекает из формулы (4.23). Действительно, независимо от элементов движения цели маневрирование на своем курсовом угле 0 или 180° ведет к максимальной скорости изменения расстояния между кораблями, так как второй член равенства (4.23) при q_r = 0° (180°) приобретает максимальное значение.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Маневрирование корабля. Метод относительного движения. Треугольники маневрирования, их характеристика и приемы решения. Основные элементы маневрирования

Страницы работы

Содержание работы

4.1. Общие положения и основные определения

Содержанием дисциплины «Тактическое маневрирование» является изучение относительного перемещения маневрирующих кораблей для занятия выгодного положения относительно объекта маневра.

Из двух маневрирующих кораблей объектом маневра принято считать тот из них, относительно которого определяются последующие положения другого корабля. Объект маневра обозначается буквой К.

Корабль, положение которого определяется либо изменяется относительно объекта маневра, называется маневрирующим и обозначается буквой М.

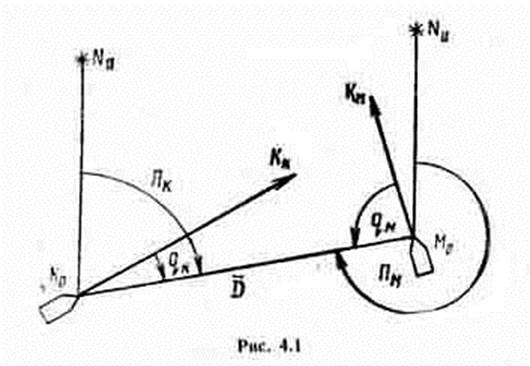
Таким образом, к элементам позиции маневрирующего корабля относятся: пеленг на маневрирующий корабль П или курсовой угол q_к и дистанция D. Так как при маневрировании используются только истинные пеленги и курсы, они обозначаются П, К, а не ИП, ИК, как в навигации.

Основными методами, применяемыми для изучения закономерностей, свойственных изменению элементов позиции маневрирующего корабля в ходе маневра, а также при практическом решении задач маневрирования, являются:

— метод относительного движения;

— метод, основанный на использовании основных элементов маневрирования.

4.2 Метод относительного движения

При двустороннем маневрировании установление законов изменения элементов позиции затруднено вследствие одновременного перемещения маневрирующих кораблей. Поэтому в тактическом маневрировании применяют метод относительного движения. Метод относительного движения заключается в замене двустороннего маневрирования как бы односторонним, при котором движение маневрирующего корабля рассматривается относительно условно неподвижного объекта маневра.

Относительным движением называется движение тела по отношению к подвижной системе координат. Движение самой подвижной системы координат относительно неподвижной системы координат называется переносным, а движение тела относительно системы координат, условно принятой за неподвижную, называется абсолютным движением.

Абсолютное, переносное и относительное движение связаны между собой геометрическим соотношением

Для дальнейших рассуждений введем следующие обозначения:

С учетом принятых обозначений формула (4.1) будет иметь вид:

Так как перемещения кораблей пропорциональны скоростям, можно записать:

Таким образом, чтобы перейти к относительному движению, необходимо из абсолютного движения исключить переносное.

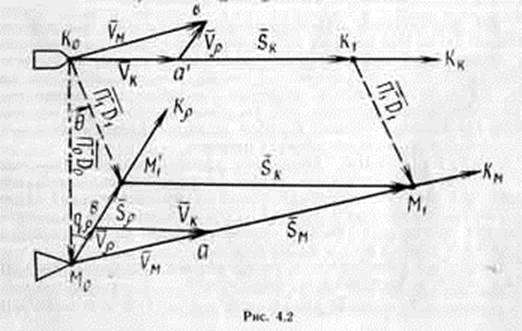
Пусть корабли М и К, находящиеся в начальный момент в точках М₀ и К₀ (рис. 4.2), следуют соответствующими курсами K_м и K_к и скоростями V_м и V_к.

Начальная позиция маневрирующего корабля определяется пеленгом П₀ и дистанцией D₀.

Таким образом, изучение закономерностей изменения элементов позиции маневрирующего корабля М относительно объекта маневра К как следствия перемещения кораблей М и К относительно поверхности Земли со скоростями V_м и V_к можно заменить изучением закономерностей изменения элементов позиции корабля М как следствия его перемещения относительно корабля К с относительной скоростью M_r. В этом и состоит сущность метода относительного движения.

Решение задач тактического маневрирования этим методом сводится к решению векторных уравнений (4.2), (4.3), (4.4) путем построения треугольников позиций, скоростей и перемещений.

4.3 Треугольники маневрирования, их характеристика и приемы решения

Треугольник К₀М₀М ‘₁ (рис. 4.2), вершинами которого являются позиции М₀, K₀, М ‘₁ маневрирующих кораблей в начале и конце маневра, а сторонами векторы начальной и конечной позиций П₀D₀, П₁D₁ и вектор относительного перемещения маневрирующего корабля S_r, называется треугольником позиций.

В треугольнике позиций вектор S_r всегда направлен от начальной позиции маневрирующего корабля к конечной относительной позиции, то есть П₁D₁ = П₀D₀ + S_r.

Источник

Наиболее тяжелые последствия вызывают столкновение судов в море. Одним из направлений понижения аварийности на судах является совершенствование средств и методов для предупреждения столкновений судов в море. Разрабатываются и внедряются специальные автоматизированные системы.

Основой безопасности расхождения судов в море является надлежащее наблюдение, по результатам которого оценивается обстановка и если необходимо следует производить расчеты для безопасного расхождения. С этой целью ПРАВИЛО 7в (МППСС-72) рекомендует вести «. радиолокационную прокладку или равноценное систематическое наблюдение за обнаруженными объектами…».

Сейчас, насколько возможно, рассмотрим и теоретически обоснуем радиолокационную прокладку, а также и равноценное ей систематическое наблюдение.

ВЕКТОРОМ называется величина, определяющаяся своим численным значением и направлением в пространстве, подчиняющаяся правилу геометрического сложения.

В математике с векторами производятся все математические действия. Действия сложения и вычитания двух векторов возможно осуществить двумя независимыми способами: геометрическим и аналитическим.

В нашем случае будем рассматривать только два математических действия: сложение и вычитание на плоскости и только геометрическим способом.

Вектор геометрически отображается стрелкой ( РИС. 1 ):

􀂃 направление стрелки указывает куда совершается движение.

А

РИС. 1 вектор скорости – как количественную, так и её направление.

Символика: V – скорость; V – вектор скорости.

Точка А – начало вектора,

точка В – конец вектора.

Одним из основных элементов в радиолокационной

прокладке является вектор скорости.

А Отличие скорости от вектора скорости в том,

что скорость выражает количественную величину,а

1.1 СЛОЖЕНИЕ ДВУХ ВЕКТОРОВ СКОРОСТЕЙ.

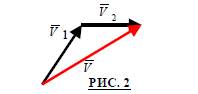
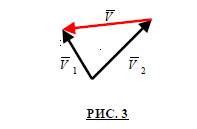
Разностью двух скоростных векторов V₁ и V₂ является скоростной вектор V полученный от построения ВЕКТОРНОГО СКОРОСТНОГО ТРЕУГОЛЬНИКА, две стороны которого являются V₁ и V₂ построенных так, что их начало расположено в одной точке, а концы их соеденены с вектором V, направление которого всегда направлено в сторону уменьшаемого вектора. ( РИС. 3 ).

Любое движение, морское или сухопутное, можно рассматривать двояко, т.е. как ОТНОСИТЕЛЬНОЕ или как ИСТИННОЕ.

ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ, это движение, контроль за которым ведется относительно любого ПОЛЮСА, выбранного самим наблюдателем. Полюсом может быть любой ориентир на поверхности Земли, кроме географических полюсов Земли.

ИСТИННОЕ ДВИЖЕНИЕ, это движение по поверхности Земли, контроль за которым осуществляется относительно земных географических ПЛЮСОВ.( Широтой и долготой ). Безусловно, такое истинное движение не будет обсалютно истинным движением, которое может быть получено только с учетом вращения Земли, ее движением по эклиптике и т. д.

2.1 ОТНОСИТЕЛЬНАЯ ПРОКЛАДКА.

Относительная радиолокационная прокладка получила широкое распространение в судовождении. В условиях ограниченной видимости с помощью РЛС можно качественно оценить окружающую обстановку при условии ведения радиолокационной прокладки.

Если РЛС стабилизирована по КУРСУ или по СЕВЕРУ в режиме относительного движения, то наблюдатель на экране РЛС видит только перемещение эхо-сигнала относительно своего судна, считая себя в центре развертки РЛС и своего движения не видит. Это наблюдаемое движение является ОТНОСИТЕЛЬНЫМ ДВИЖЕНИЕМ. Перенеся такое движение на маневренный планшет или лист бумаги, получим относительную радиолокационную прокладку, которая отображает взаимное расположение судов по времени и позволяет оперативно решить вопросы:

􀂃 насколько опасно плавание со встречными судами, т.е. на каком кратчайшем расстоянии разойдемся с судами ( Дкр ) ;

􀂃 как быстро наступит момент кратчайшего сближения нашего судна с другими (Ткр).

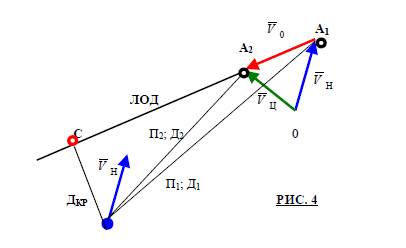
Суть ОТНОСИТЕЛЬНОЙ Р.Л. ПРОКЛАДКИ заключается в следующем (РИС. 4) :

Движущейся эхо-сигнал цели по ЛОД имеет место, где он сблизится с нашим судном на самое кратчайшее расстояние- Д_КР. Перпендикуляр, опущенный из центра планшета или точки

О на листе бумаги (с расположения нашего судна) на ЛОД, есть Д_КР, а пересечение этого перпендикуляра с ЛОД даст точку С при выходе эхо-сигнала в которую между нашим и наблюдаемым судами будет самое близкое расстояние.

Время, необходимое для перехода эхо-сигнала цели от первой точки наблюдения А₁ до выхода в точку кратчайшего сближения С, принято называть Т_КР, которое найдем:

Где: А₁С – расстояние от первой точки наблюдения до точки кратчайшего сближения с целью;

Преобразуем предыдущую формулу и получим неизвестное V_ц :

Для нахождения неизвестного вектора цели необходимо геометрически сложить два известных вектора, т.е. построить векторный скоростной треугольник. Из РЛ прокладки, имеем вектор относительной скорости V₀ (РИС. 4), к его началу, своим концом, построим вектор нашей скорости. Суммарный третий вектор, проведенный из начала вектора нашей скорости на конец вектора относительной скорости даст вектор скорости цели V_ц. Его направление это истинный курс цели, а длина, во временном масштабе, это истинная скорость цели. При построении векторного скоростного треугольника существуют три постоянные свойства:

ПЕРВОЕ свойство:Вектор нашей скорости ВСЕГДА строится таким образом, что его конец распологается в первой точке наблюдения.

ТРЕТЬЕ свойство:Вектор относительной скорости ВСЕГДА начинается на конце вектора нашей скорости и заканчивается на конце вектора скорости цели.

Дата добавления: 2020-11-27 ; просмотров: 248 ; Мы поможем в написании вашей работы!

Источник

Закономерности относительного движения

Задачи расчета маневра безопасного расхождения с судами-целями проще и надежнее решать в режиме относительного движения.

Определяющее значение для оценки опасности столкновения судов имеет четкое знание судоводителем закономерностей, указанного выше, относительного движения. Для того чтобы произвести оценку ситуации, определить опасность столкновения и решить задачу необходимо четко знать закономерности перемещения судов в режиме относительного движения. Для их понимания нет необходимости производить какие-либо вычисления, а надо только знать факторы, от которых зависит изменения обстановки при маневрировании собственного и других судов.

Характер изменения относительного движения зависит от трех факторов:

1) от расположения других судов относительно курса собственного судна (справа или слева);

2) величины курсового угла между линией относительного движения и ДП своего судна (курсового угла ЛОД 90° впереди траверза, на траверзе, позади траверза).

3) расположением ЛОД относительно собственного суда (пересекает курс по носу, проходит через нас или пересекает линию курса по корме).

Изменение относительного движения характеризуют двумя параметрами:

— направлением ОЛОД относительно первоначальной ЛОД (по часовой стрелке или против часовой стрелки (вправо или влево));

— изменением расположения ОЛОД по отношению к собственному судну (удаляется от нас или приближается к нам).

Основным элементомвекторного треугольника скоростей является вектор относительного движения V₀, направление и величина которого характеризует динамику развития ситуации расхождения. Поэтому четкому пониманию ситуации служит систематизированная схема перемещений отметок объектов.

По характеру перемещений отметок по ЛОД их делят на три вида:

1) эхо-сигнал перемещается параллельно курсовой черте нашего судна;

2) эхо-сигнал пересекает линию нашего курса;

3) эхо-сигнал не перемещается по экрану, пеленг и дистанция до него не изменяется, следа послесвечения нет. Такое судно называют «сателлит».

При перемещении эхо-сигнала параллельно курсовой черте нашего судна различают четыре основных случая образований ЛОД (см. рисунок):

Случай 1. Суда следуют встречными курсами (причем может быть больше, меньше или равно ):

= + .

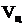
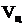
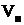
Случай 2. Наше судно обгоняетсудно-цель:

= — ;

> .

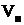
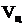
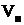
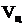
Случай 3. Судно-цель обгоняет наше судно:

= — ;

> .

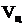
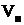
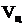
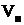
Случай 4. Судно-цель неподвижно, относительная скорость ее равна скорости нашего судна, а вектор направлен от носа к корме

= ;

=0;

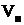
Примечание:

При перемещении эхо-сигналов целей параллельно курсовой черте существуют следующие закономерности:

— эхо-сигнал неподвижного объекта всегда перемещается параллельно линии курса собственного судна при любых его измерениях;

— при изменениях скорости собственного или других судов параллельность перемещения эхо-сигналов курсовой черте сохраняется.

Дата добавления: 2018-06-27 ; просмотров: 673 ; Мы поможем в написании вашей работы!

Источник