в чем заключается процесс обучения алгоритма k ближайших соседей
Классификатор kNN
kNN расшифровывается как k Nearest Neighbor или k Ближайших Соседей — это один из самых простых алгоритмов классификации, также иногда используемый в задачах регрессии. Благодаря своей простоте, он является хорошим примером, с которого можно начать знакомство с областью Machine Learning. В данной статье рассмотрен пример написания кода такого классификатора на python, а также визуализация полученных результатов.
Задача классификации в машинном обучении — это задача отнесения объекта к одному из заранее определенных классов на основании его формализованных признаков. Каждый из объектов в этой задаче представляется в виде вектора в N-мерном пространстве, каждое измерение в котором представляет собой описание одного из признаков объекта. Допустим нам нужно классифицировать мониторы: измерениями в нашем пространстве параметров будут величина диагонали в дюймах, соотношение сторон, максимальное разрешение, наличие HDMI-интерфейса, стоимость и др. Случай классификации текстов несколько сложнее, для них обычно используется матрица термин-документ (описание на machinelearning.ru).
Для обучения классификатора необходимо иметь набор объектов, для которых заранее определены классы. Это множество называется обучающей выборкой, её разметка производится вручную, с привлечением специалистов в исследуемой области. Например, в задаче Detecting Insults in Social Commentary для заранее собранных тестов комментариев человеком проставлено мнение, является ли этот комментарий оскорблением одного из участников дискуссии, само же задание является примером бинарной классификации. В задаче классификации может быть более двух классов (многоклассовая), каждый из объектов может принадлежать более чем к одному классу (пересекающаяся).
Алгоритм
Исходные данные
Рассмотрим работу классификатора на примере. Для начала, нам нужно сгенерировать данные, на которых будут производиться эксперименты:
Для простоты я выбрал двумерное пространство, в котором случайным образом на участке от 0 до 5 по каждой из осей выбирается местоположение мат.ожидания двумерного гауссиана со среднеквадратичным отклонением 0.5. Значение 0.5 выбрано, чтобы объекты оказались достаточно хорошо разделимыми (правило трех сигм).
Чтобы посмотреть на полученную выборку, нужно выполнить следующий код:
Вот пример полученного в результате выполнения этого кода изображения:
Получение обучающей и тестовой выборки
Итак, у нас имеется набор объектов, для каждого из которых задан класс. Теперь нам нужно разбить это множество на две части: обучающую выбору и тестовую выборку. Для этого служит следующий код:
Реализация классификатора
Теперь, имея обучающую выборку, можно реализовать и сам алгоритм классификации:
Для определения расстояния между объектами можно использовать не только евклидово расстояние: также применяются манхэттенское расстояние, косинусная мера, критерий корелляции Пирсона и др.
Примеры выполнения
Теперь можно оценить, насколько хорошо работает наш классификатор. Для этого сгенерируем данные, разобьем их на обучающую и тестовую выборку, произведем классификацию объектов тестовой выборки и сравним реальное значение класса с полученным в результате классификации:
Для оценки качества работы классификатора используются различные алгоритмы и различные меры, более подробно можно почитать здесь: wiki
Теперь осталось самое интересное: показать работу классификатора графически. В приведенных ниже картинках я использовал 3 класса, в каждом по 40 элементов, значение k для алгоритма взял равным трем.
Для вывода этих картинок использован следующий код:
Заключение
kNN — один из простейших алгоритмов классификации, поэтому на реальных задачах он зачастую оказывается неэффективным. Помимо точности классификации, проблемой этого классификатора является скорость классификации: если в обучающей выборке N объектов, в тестовой выборе M объектов, а размерность пространства — K, то количество операций для классификации тестовой выборки может быть оценено как O(K*M*N). И тем не менее, алгоритм работы kNN является хорошим примером для начала знакомства с Machine Learning.
🤖 Метод k-ближайших соседей (k-nearest neighbour)
Alex Maszański
Пример классификации k-ближайших соседей.
Теоретическая составляющая алгоритма k-NN
Помимо простого объяснения, необходимо понимание основных математических составляющих алгоритма k-ближайших соседей.
Формула вычисления Евклидова расстояния:
MinMax-нормализация осуществляется следующим образом:
в данном случае все значения будут находиться в диапазоне от 0 до 1; дискретные бинарные значения определяются как 0 и 1.
где σ – среднеквадратичное отклонение. В данном случае большинство значений попадает в диапазон.
Каков порядок действий?
Реализация на языке Python
Набор данных состоит из 15 столбцов, таких как sex (пол), fare (плата за проезд), p_class (класс каюты), family_size (размер семьи), и т. д. Главным признаком, который мы и должны предсказать в соревновании, является survived (выжил пассажир или нет).
Дополнительный анализ показал, что находящиеся в браке люди имеют больший шанс на то, чтобы быть спасенными с корабля. Поэтому были добавлены еще 4 столбца, переименованные из Name (Имя), которые обозначают мужчин и женщин в зависимости от того, были они женаты или нет (Mr, Mrs, Mister, Miss).
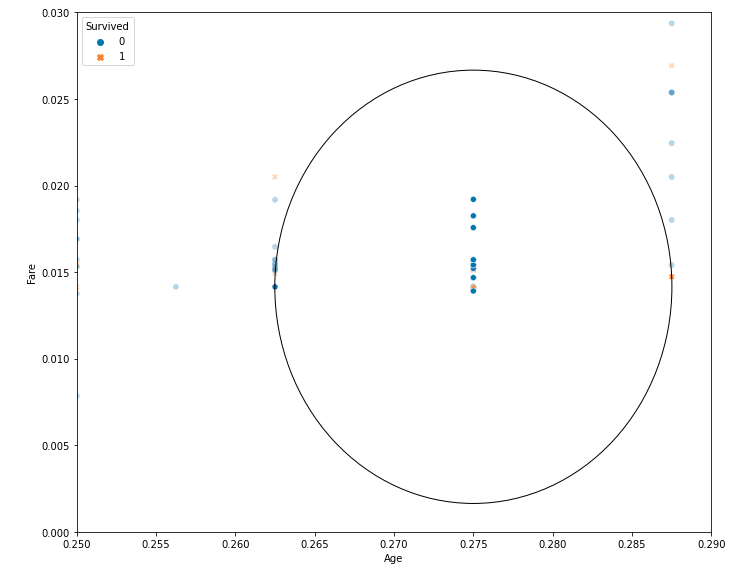
Чтобы наглядно продемонстрировать функциональность k-NN для предсказания выживания пассажира, мы рассматриваем только два признака: age (возраст), fare (плата за проезд).
Здесь вероятность выживания составляет 0.3 – 30%.
Результат работы кода:
Как видите, на графике показаны 20 ближайших соседей, 14 из которых связаны с теми, кто не выжил (вероятность 0,7 – 70%), а 6 связаны с выжившими (вероятность 0,3 – 30%).
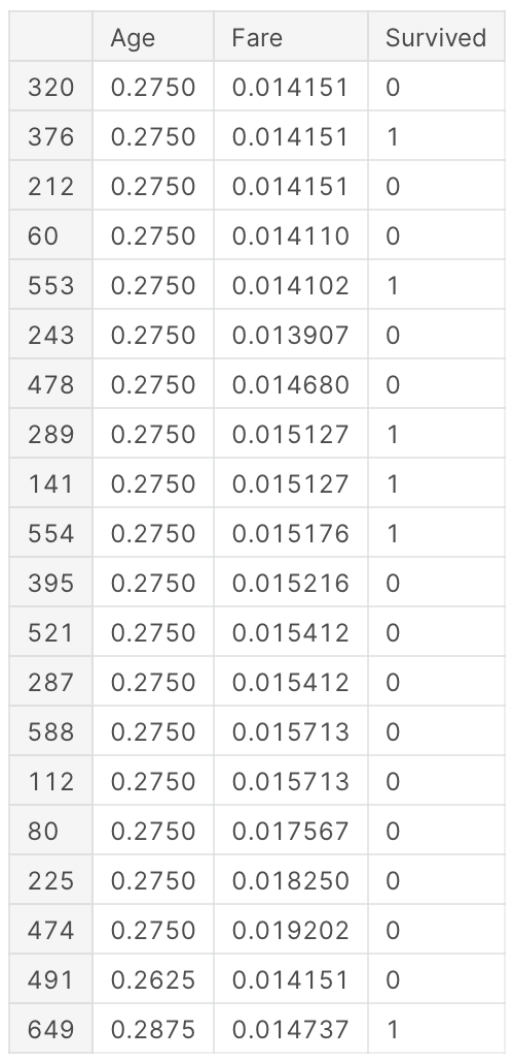
Мы можем просмотреть первые 20 ближайших соседей для заданных параметров при помощью следующего кода:
Результатом будет таким:
Выбор Оптимального значения для k-NN
Не существует конкретного способа определить наилучшее значение для k, поэтому нам нужно попробовать несколько значений, чтобы найти лучшее из них. Но чаще всего наиболее предпочтительным значением для k является 5:
Преимущества и Недостатки
В заключение
Метод k-ближайших соседей (k-nearest neighbors) – это простой алгоритм машинного обучения с учителем, который можно использовать для решения задач классификации и регрессии. Он прост в реализации и понимании, но имеет существенный недостаток – значительное замедление работы, когда объем данных растет.
Классификация данных методом k-ближайших соседей
Преимуществом статистических методов является их хорошая математическая обоснованность, недостатком — низкая объясняющая способность. Использование вероятностных оценок позволяет с высокой точностью предсказать к какому классу относится объект, но не позволяет сказать почему. Поэтому результаты статистических методов классификации могут оказаться сложными для понимания и интерпретации результатов.
Одной из важнейших задач анализа данных является классификация — отнесение объектов предметной области к заранее определённым группам, называемым классами. При этом каждому классу должны принадлежать объекты, близкие по своим свойствам. Обобщая свойства известных объектов класса на новые, отнесённые к нему объекты, можно получать знания о них.
Задача классификации решается с помощью аналитических моделей, называемых классификаторами. Классифицировать объект означает предъявить набор его признаков (обычно представленных в виде вектора) на вход модели-классификатора, которая должна присвоить ему метку или номер класса. В настоящее время разработано большое количество различных видов классификаторов, для построения которых используются как статистические методы (логистическая регрессия, дискриминантный анализ), так и методы машинного обучения (нейронные сети, деревья решений и др.).
Необходимость использования в анализе данных большого числа разнообразных методов классификации, обусловлена тем, что решаемые с её помощью задачи могут иметь свои особенности, связанные, например, с представлением исходных данных, их количеством и качеством, что требует выбора адекватного классификатора. Поэтому выбор классификатора, соответствующего особенностям решаемой задачи анализа, является важным фактором получения правильного решения.
Отнесение классификации к интеллектуальным технологиям анализа данных обусловлено тем, что в повседневной жизни сознание человека, в поле которого постоянно попадают новые объекты окружающего мира, сопоставляет их с уже известными объектами и оценивает степень их сходства. Затем, на основе это оценки объект ассоциируется с определённой группой (классом). Таким образом, классификация является наиболее «естественным» для человеческого интеллекта способом получения знаний о процессах и явлениях, происходящих в окружающем мире.
Учитывая сказанное, можно предположить, что все методы классификации в том или ином виде будут использовать формализованное понятие «сходства», мера которого будет оцениваться с помощью некоторой функции. В статистических методах анализа мерой сходства является вероятность принадлежности объекта классу, которая оценивается для каждого класса, после чего выбирается тот из них, для которого эта вероятность наибольшая.
В метрических методах мерой сходства является расстояние (например, евклидово) в векторном пространстве, где каждый объект представлен своим вектором признаков. Логика здесь проста: новый объект скорее всего принадлежит к тому же классу, что и большинство соседних с ним объектов. Метрические методы как правило используются для построения классификаторов на основе машинного обучения.
Преимуществом статистических методов является их хорошая математическая обоснованность, недостатком — низкая объясняющая способность. Использование вероятностных оценок позволяет с высокой точностью предсказать к какому классу относится объект, но не позволяет сказать почему. Поэтому результаты статистических методов классификации могут оказаться сложными для понимания и интерпретации результатов.
Недостатком метрических методов является их эвристический характер — они могут дать неточное и неоднозначное решение, но считающееся приемлемым в большинстве практически значимых случаев. Однако при этом они имеют высокую объясняющую способность и поэтому их результаты проще интерпретировать. В простейшем случае можно использовать правило: объект относится к тому же классу, что и большинство его ближайших соседей.
Типичным представителем методов классификации, использующих эту логику, является метод k-ближайших соседей — k-nearest neighbors algorithm (KNN). Метод был впервые разработан Эвелином Фиксом и Джозефом Лоусоном Ходжесом в 1951 году, и позднее развит Томасом Ковером.
Метод относится к классу непараметрических, т.е. не требует предположений о том, из какого статистического распределения была сформирована обучающее множество. Следовательно, классификационные модели, построенные с помощью метода KNN также будут непараметрическими. Это означает, что структура модели не задаётся жёстко изначально, а определяется данными.
Поскольку признаки, на основе которых производится классификация могут иметь различную физическую природу и, соответственно, диапазоны значений, для улучшения результатов классификации будет полезно выполнить нормализацию обучающих данных.
Алгоритм
На фазе классификации предъявляется новый объект, для которого метка класса не задана. Для него определяются k ближайших (в смысле некоторой метрики) предварительно классифицированных наблюдений. Затем выбирается класс, которому принадлежит большинство из k ближайших примеров-соседей, и к этому же классу относится классифицируемый объект.
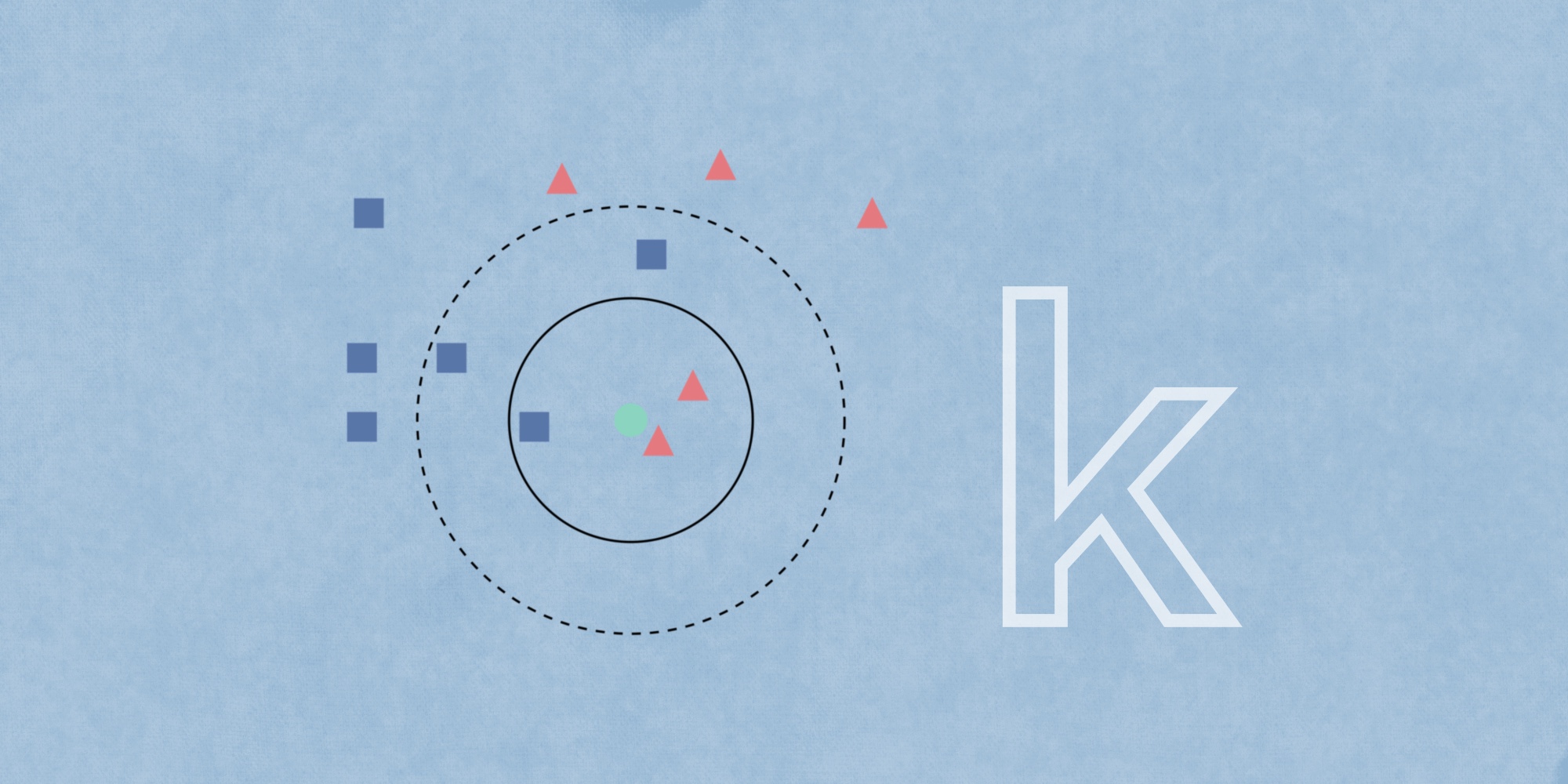
Поясним работу алгоритма с помощью рисунка.
Рисунок 1 – Работа алгоритма KNN
Определение класса нового объекта
В простейшем случае класс нового объекта может быть определён простым выбором наиболее часто встречающегося класса среди k примеров. Однако на практике это не всегда удачное решение, например, в случае когда частота появления для двух или более классов оказывается одинаковой. Кроме этого разумно предположить, что не все обучающие имеют одинаковую значимость для определения класса. В этом случае используют некоторую функцию, с помощью которой определяется класс, называемую функцией сочетания (combination function).
В обычном случае используют так называемое простое невзвешенное голосование (simple unweighted voting). При это предполагается, что все k примеров имеют одинаковое право «голоса» независимо от расстояние до классифицируемого объекта.
Однако, логично предположить, что чем дальше пример расположен от классифицируемого объекта в пространстве признаков, тем ниже его значимость для определения класса. Поэтому для улучшения результатов классификации вводят взвешивание примеров в зависимости от их удалённости. В этом случае используют взвешенное голосование (weighted voting).
Выбор значения параметра k
Кроме этого, следует учитывать, что использование небольших значений k увеличивает влияние шумов на результаты классификации, когда небольшие изменения в данных приводят к большим изменениям в результатах классификации. Но при этом границы классов оказываются более выраженными (класс при голосовании побеждает с большим счётом).
Напротив, если значение параметра слишком велико, то в процессе классификации принимает участие много объектов, относящихся к разным классам. Такая классификация оказывается слишком грубой и плохо отражает локальные особенности набора данных. Таким образом, выбор параметра k является компромиссом между точностью и обобщающей способностью модели.
При больших значениях параметра k уменьшается зашумленность результатов классификации, но снижается выраженность границ классов.
В задачах бинарной классификации бывает целесообразно выбрать k как нечетное число, так как это позволяет избежать равенства «голосов» при определении класса для нового наблюдения.
Особенности работы алгоритма
Если значения признаков непрерывные, то в качестве меры расстояния между объектами обычно используется расстояние Евклида, а если категориальные, то может использоваться расстояние Хэмминга.
Алгоритма KNN является чувствительным к дисбалансу классов в обучающих данных: алгоритм «склонен» к смещению решения в сторону доминирующего класса, поскольку относящиеся к нему объекты просто чаще попадают в число ближайших соседей. Одним из способов решения данной проблемы является применение различных способов взвешивания при «голосовании».
Рисунок 2 – Обратное соседство
Ещё одной проблемой алгоритма KNN, характерной, впрочем, и для большинства методов классификации, является различная значимость признаков с точки зрения определения класса объектов. Учет фактора значимости признаков в алгоритме может позволить повысить точность классификации.
Для этого аналитик или эксперт на основе субъективной, либо некоторой формальной оценки может задать уровень значимости признака, выразив его с помощью числового коэффициента (обозначим его s от англ significance — значимость), который учитывается при вычислении расстояния между примерами и классифицируемым объектом:
Численный пример
Рассмотрим простой численный пример работы алгоритма KNN, проиллюстрированный на рисунке 3.
Рисунок 3 – Численный пример
Пусть имеется набор данных о заёмщиках банка часть из которых допустили просрочку по платежу (таблица 1). Признаками являются возраст и среднемесячный доход. Метками класса в поле «Просрочено» будут «Да» и «Нет».
На рисунке 3 оранжевыми кружками представлены объекты класса «Нет», а фиолетовыми класса «Да». Синим квадратом отображается классифицируемый объект (новый заёмщик).
Задача заключается в том, чтобы выполнить классификацию нового заёмщика для которого A_1=42 и A_2=34 с целью оценить возможность просрочки им платежей.
Таким образом, из трёх ближайших соседей (на рисунке расположены внутри круга) классифицируемого объекта два имеют класс «Да», а один — «Нет». Следовательно, путём простого невзвешенного голосования определяем его класс как «Да». На основании работы классификатора делаем вывод, что заёмщик с заданными характеристиками может допустить просрочку по выплате кредита.
Области применения алгоритма
Алгоритм KNN может применяться практически во всех задачах классификации, особенно в тех случаях, когда оценить параметры вероятностного распределения данных сложно или невозможно. Наиболее типичными приложениями алгоритма KNN являются:
Достоинства и недостатки алгоритма
В заключение отметим достоинства и недостатки алгоритма KNN. К достоинствам алгоритма можно отнести.
К недостаткам алгоритм KNN можно отнести:
Алгоритм K-ближайших соседей в Python и Scikit-Learn
Алгоритм K-ближайших соседей (KNN) – это тип алгоритмов контролируемого машинного обучения. KNN чрезвычайно прост в реализации в своей самой базовой форме и все же выполняет довольно сложные задачи классификации. Это ленивый алгоритм обучения, так как он не имеет специальной фазы обучения. Скорее, он использует все данные для обучения при классификации новой точки данных или экземпляра. KNN-это непараметрический алгоритм обучения, который означает, что он ничего не предполагает о базовых данных. Это чрезвычайно полезная функция, поскольку большинство реальных данных на самом деле не следуют никаким теоретическим предположениям, например линейной разделимости, равномерного распределения и т. Д.
В этой статье мы увидим, как KNN может быть реализован с помощью библиотеки Scikit-Learn Python. Но перед этим давайте сначала исследуем теорию, лежащую в основе KNN, и посмотрим, каковы некоторые плюсы и минусы этого алгоритма.
Теория
Интуиция, лежащая в основе алгоритма KNN, является одним из самых простых из всех контролируемых алгоритмов машинного обучения. Он просто вычисляет расстояние от новой точки данных до всех других обучающих точек данных. Расстояние может быть любого типа, например евклидово или манхэттенское и т. Д. Затем он выбирает K-ближайшие точки данных, где K может быть любым целым числом. Наконец, он присваивает точку данных классу, к которому принадлежит большинство из K точек данных.
Рассмотрим этот алгоритм в действии на простом примере. Предположим, у вас есть набор данных с двумя переменными, который при построении графика выглядит так, как показано на следующем рисунке.
Ваша задача состоит в том, чтобы классифицировать новую точку данных с “X” в “Синий” класс или “Красный” класс. Координатными значениями точки данных являются и. Предположим, что значение K равно 3. Алгоритм KNN начинается с вычисления расстояния точки X от всех точек. Затем он находит 3 ближайшие точки с наименьшим расстоянием до точки X. Это показано на рисунке ниже. Три ближайших пункта окружены.
Последний шаг алгоритма KNN состоит в том, чтобы присвоить новую точку классу, к которому принадлежит большинство из трех ближайших точек. Из рисунка выше видно, что две из трех ближайших точек относятся к классу “Красных”, а одна-к классу “Синих”. Поэтому новая точка данных будет классифицирована как “Красная”.
Плюсы и минусы KNN
В этом разделе мы представим некоторые плюсы и минусы использования алгоритма KNN.
Плюсы
Аферы
Реализация алгоритма KNN с помощью Scikit-Learn
Примечание : Код, приведенный в этом руководстве, был выполнен и протестирован с помощью Python Jupyter notebook.
Набор данных
Импорт библиотек
Импорт набора данных
Чтобы импортировать набор данных и загрузить его в наш фрейм данных pandas, выполните следующий код:
Чтобы увидеть, как на самом деле выглядит набор данных, выполните следующую команду:
Выполнение приведенного выше скрипта приведет к отображению первых пяти строк нашего набора данных, как показано ниже:
| Ирис-сетоза | 0 | 0.2 | 3.5 | 1.4 | 5.1 |
| Ирис-сетоза | 1 | 0.2 | 3.0 | 1.4 | 4.9 |
| Ирис-сетоза | 2 | 0.2 | 3.2 | 1.3 | 4.7 |
| Ирис-сетоза | 3 | 0.2 | 3.1 | 1.5 | 4.6 |
| Ирис-сетоза | 4 | 0.2 | 3.6 | 1.4 | 5.0 |
Предварительная обработка
Следующий шаг-разбить наш набор данных на его атрибуты и метки. Для этого используйте следующий код:
Переменная X содержит первые четыре столбца набора данных (т. е. атрибуты), в то время как y содержит метки.
Тестовый раскол поезда
Чтобы избежать переобучения, мы разделим наш набор данных на обучающие и тестовые разбиения, что даст нам лучшее представление о том, как работает наш алгоритм на этапе тестирования. Таким образом, наш алгоритм тестируется на невидимых данных, как это было бы в производственном приложении.
Чтобы создать тренировочные и тестовые разбиения, выполните следующий сценарий:
Приведенный выше сценарий разбивает набор данных на 80% обучающих данных и 20% тестовых данных. Это означает, что из общего числа 150 записей обучающий набор будет содержать 120 записей, а тестовый набор-30 из них.
Масштабирование объектов
Прежде чем делать какие-либо реальные прогнозы, всегда полезно масштабировать объекты так, чтобы все они могли быть равномерно оценены. Википедия довольно хорошо объясняет эти рассуждения:
Поскольку диапазон значений исходных данных сильно варьируется, в некоторых алгоритмах машинного обучения целевые функции не будут работать должным образом без нормализации. Например, большинство классификаторов вычисляют расстояние между двумя точками по евклидову расстоянию. Если один из объектов имеет широкий диапазон значений, то расстояние будет определяться этим конкретным объектом. Поэтому диапазон всех объектов должен быть нормализован таким образом, чтобы каждый объект вносил примерно пропорциональный вклад в конечное расстояние.
Алгоритм градиентного спуска (который используется в обучении нейронных сетей и других алгоритмах машинного обучения) также быстрее сходится с нормализованными функциями.
Следующий сценарий выполняет масштабирование объектов:
Обучение и прогнозы
Обучить алгоритм KNN и делать с его помощью прогнозы чрезвычайно просто, особенно при использовании Scikit-Learn.
Последний шаг-сделать прогнозы по нашим тестовым данным. Для этого выполните следующий сценарий:
Оценка алгоритма
Вывод вышеприведенного скрипта выглядит следующим образом:
Результаты показывают, что наш алгоритм KNN смог классифицировать все 30 записей в тестовом наборе со 100% точностью, что является отличным результатом. Хотя алгоритм очень хорошо работает с этим набором данных, не ожидайте одинаковых результатов со всеми приложениями. Как отмечалось ранее, KNN не всегда работает так же хорошо с высокомерными или категориальными характеристиками.
Сравнение частоты ошибок со значением K
В разделе “Обучение и прогнозирование” мы говорили, что нет способа заранее узнать, какое значение K дает наилучшие результаты с первого раза. Мы случайно выбрали 5 в качестве значения K, и это просто привело к 100% – ной точности.
Один из способов помочь вам найти наилучшее значение K-построить график значения K и соответствующей частоты ошибок для набора данных.
В этом разделе мы построим среднюю ошибку для прогнозируемых значений тестового набора для всех значений K в диапазоне от 1 до 40.
Для этого сначала вычислим среднее значение ошибки для всех прогнозируемых значений, где K колеблется от 1 до 40. Выполните следующий сценарий:
Следующий шаг-построить график значений error против значений K. Выполните следующий сценарий для создания сюжета:
Выходной график выглядит следующим образом:
Из выходных данных мы видим, что средняя ошибка равна нулю, когда значение K находится между 5 и 18. Я бы посоветовал вам поиграть со значением K, чтобы увидеть, как оно влияет на точность предсказаний.
Ресурсы
Хотите узнать больше о Scikit-Learn и других полезных алгоритмах машинного обучения? Я бы рекомендовал проверить некоторые более подробные ресурсы, например онлайн-курс:
Хотя чтение сообщений в блогах, подобных этому, является отличным началом, большинство людей, как правило, лучше учатся с визуальными эффектами, ресурсами и объяснениями из курсов, подобных приведенным выше.
Вывод
KNN-это простой, но мощный алгоритм классификации. Он не требует обучения для составления прогнозов, что, как правило, является одной из самых сложных частей алгоритма машинного обучения. Алгоритм KNN широко используется для поиска сходства документов и распознавания образов. Он также использовался для разработки рекомендательных систем, а также для уменьшения размерности и предварительной обработки шагов компьютерного зрения, в частности задач распознавания лиц.
Отсюда я бы посоветовал вам реализовать алгоритм KNN для другого набора данных классификации. Варьируйте размер теста и тренировки вместе со значением K, чтобы увидеть, как ваши результаты отличаются и как вы можете повысить точность своего алгоритма. Хорошая коллекция классификационных наборов данных доступна здесь для вас, чтобы играть.
К каким еще приложениям вы применили алгоритм KNN? Как это у тебя получилось? Дайте нам знать в комментариях!