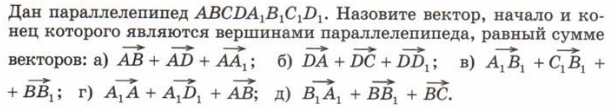в чем заключается правило параллелепипеда рисунок обязательно
Тема: Правило параллелепипеда.
Решенные задачи писать не нужно. Они как образец для решения д/з.
1. Записать правило параллелепипеда. Рассмотреть доказательство. Зарисовать рисунок.
Для сложения компланарных векторов, так как все они лежат в одной плоскости, можно использовать правила сложения известные из планиметрии, а именно: правило треугольника, правило параллелограмма и правило многоугольника.
Что же касается некомпланарных векторов, то для построения их суммы используют правило параллелепипеда. Опишем его.
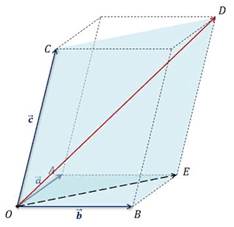
Рассмотрим некомпланарные векторы 
.
От произвольной точки О пространства отложим векторы 
, 
и 
равные векторам соответственно.
На полученных векторах можно построить параллелепипед так, чтобы они являлись его рёбрами.
Построим вектор суммы векторов 
, 
и 
при этом последовательно их складывая.
Вектором суммы векторов , по правилу параллелограмма будет вектор 
. Вектором суммы векторов и по тому же правилу будет вектор 
. Вектор равен сумме векторов , и , а значит равен сумме векторов 
.
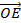
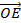
Отсюда правило параллелепипеда можно сформулировать так:
Если отложить некомпланарные векторы от некоторой точки пространства О и построить на них параллелепипед, то диагональ OD параллелепипеда будет выражать вектор суммы данных векторов.
2. Воспользуемся сформулированным только что правилом и выполним задание.
а) т.к. эти векторы отложены от одной точки и являются рёбрами данного параллелепипеда, то вектор их суммы будет задавать диагональ параллелепипеда, одним из концов которой будет точка начала данных векторов А. Так мы получим вектор 
.
в) В данном случае векторы не имеют общего начала, а имеют общий конец.
Выразим каждый из данных векторов через противоположный.
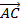
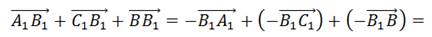
Урок «Правило параллелепипеда» 10 класс
Конспект урока №2: «Правило параллелепипеда»
Тема урока : Правило параллелепипеда
Тип урока : Урок изучения и первичного закрепления новых знаний
Учебная задача урока : В совместной деятельности с учащимися овладеть теоретическими знаниями и практическими навыками по теме «Правило параллелепипеда»
Правило параллелепипеда сложения трех некомпланарных векторов
Решать задачи по теме
Для чего изучается данная тема;
Как применяются знания на практике
Учебные действия формируемые на уроке :
Личностные: умение учащегося устанавливать связи между целью учебной деятельности и её мотивом, т.е. между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется, таким образом должна осуществляться осмысленная организация собственной деятельности ученика
Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что ещё неизвестно, планирование-определение последовательности промежуточных целей с учетом конечного результата, оценка-выделение и осознание учащимся того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т.е. определение цели сотрудничества, функций участников, способов взаимодействия, умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, умение доказывать собственное мнение.
Познавательные: анализ объектов с целью выделения признаков (существенных, несущественных);выдвижение гипотез и их обоснование; построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей
Методы обучения : объяснительно-иллюстративный.
Форма работы : фронтальная, индивидуальная.
Средства обучения: традиционная, презентация.
Мотивационно-ориентировочная часть (15 мин)
Операционно-познавательная часть (25 мин)
Рефлексивно-оценочная часть (5 мин)
Приветствие. Записываем число, классная работа. Кто отсутствует.
Ребята, давайте повторим, что вы изучали на прошлом уроке.
Какие векторы называются компланарными?
Какую формулировку определения компланарного вектора мы использовали на практике?
Расскажите признак компланарности векторов.
Расскажите обратный признак компланарности векторов.
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости
Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости
Постановка учебной задачи.
Для сложения компланарных векторов, так как все они лежат в одной плоскости, можно использовать правила сложения известные из планиметрии, а именно: правило треугольника, правило параллелограмма и правило многоугольника.
Что же касается некомпланарных векторов, то для построения их суммы используют правило параллелепипеда.
Цель нашего урока: Овладеть теоретическими знаниями и практическими навыками по теме «Правило параллелепипеда»
От произвольной точки О пространства отложим векторы и равные векторам и соответственно.
На полученных векторах можно построить параллелепипед так, чтобы они являлись его рёбрами.
Построим вектор суммы векторов и при этом последовательно их складывая.
Отсюда правило параллелепипеда можно сформулировать так.
Если отложить некомпланарные векторы и от некоторой точки пространства и построить на них параллелепипед, то диагональ параллелепипеда будет выражать вектор суммы данных векторов.
Воспользуемся сформулированным только что правилом и выполним задание.
Давайте изобразим полученный вектор в данном параллелепипеде.
От какой точки они отложены и какой вектор их суммы мы получим?
Изобразите полученный вектор в параллелепипеде.
Давайте выразим каждый из данных векторов через противоположный.
Изобразите полученный вектор в параллелепипеде.
Какой вектор равен ему?
Вектором полученной суммы будет какой вектор?
Изобразите полученный вектор в параллелепипеде.
Какой вектор нужно заменить?
Давайте запишем вектор суммы и изобразим его в параллелепипеде.
Презентация «Правило параллелепипеда»
Документы в архиве:
Название документа 41.
Описание презентации по отдельным слайдам:
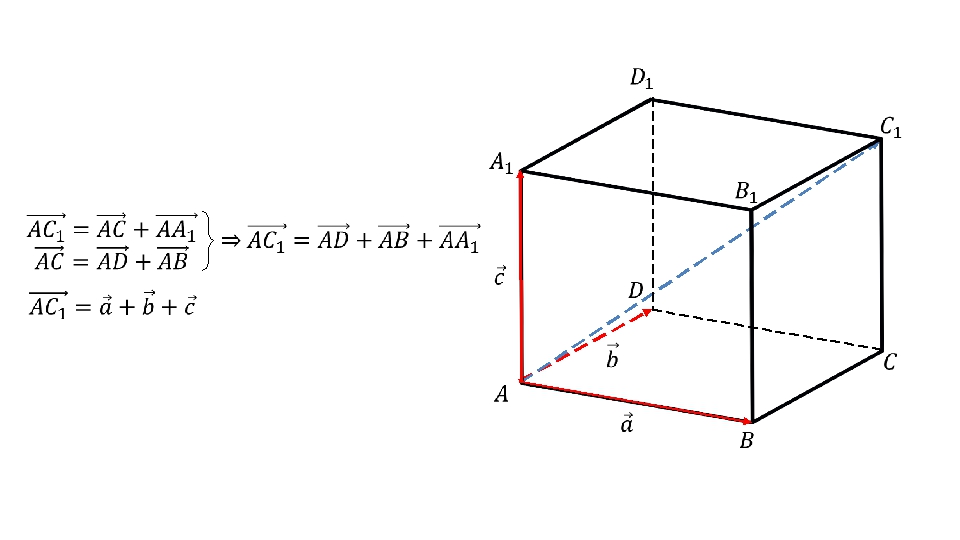
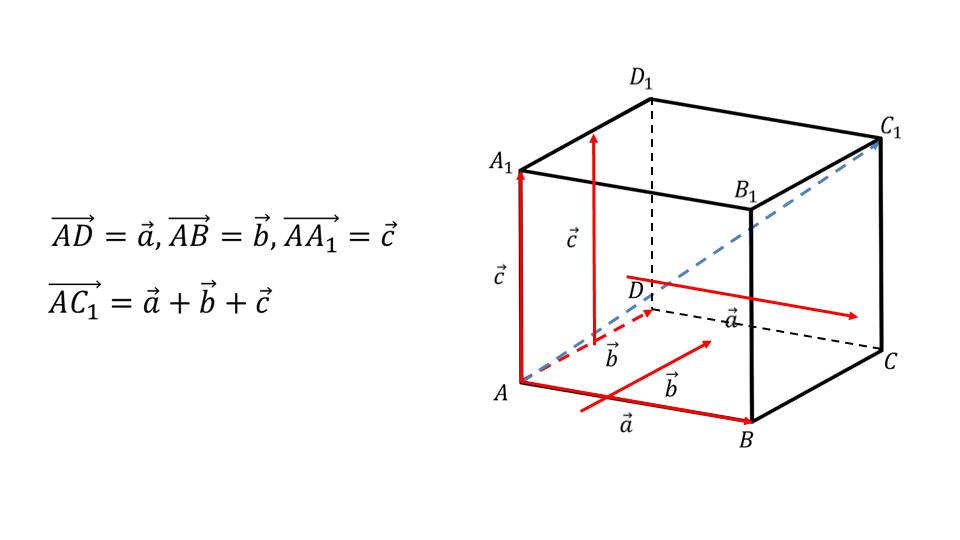
Правило параллелепипеда Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из той же точки и лежащих на трех измерениях параллелепипеда.
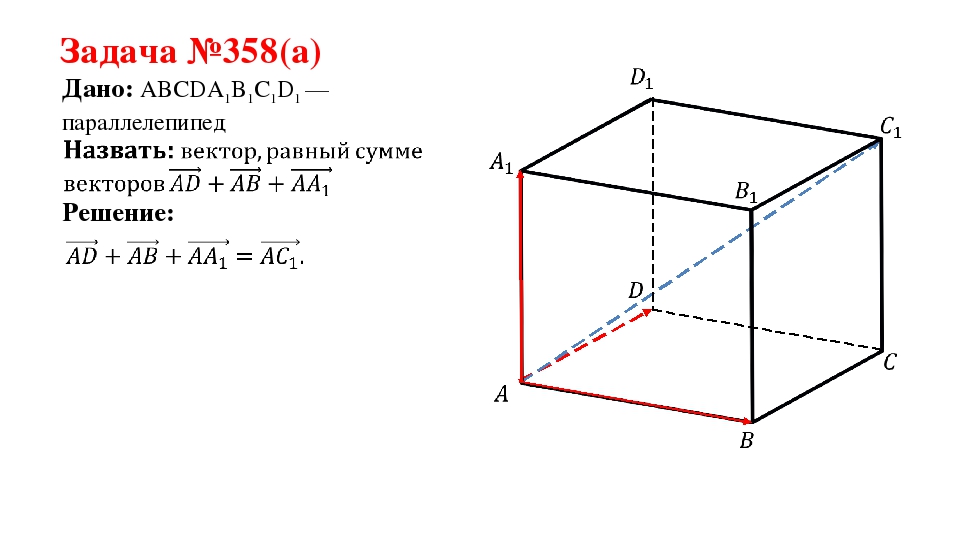
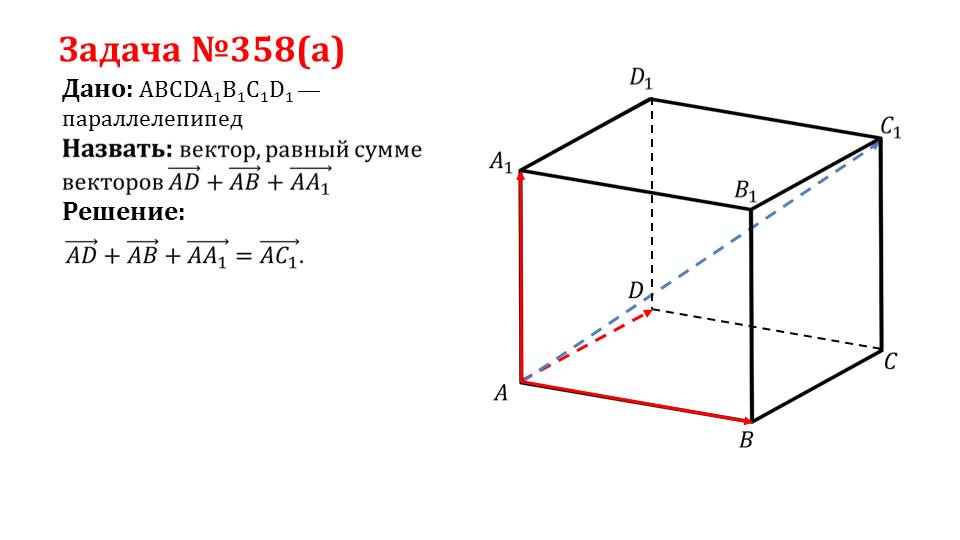
Задача №358(а) Дано: ABCDA1B1C1D1 —параллелепипед Решение:
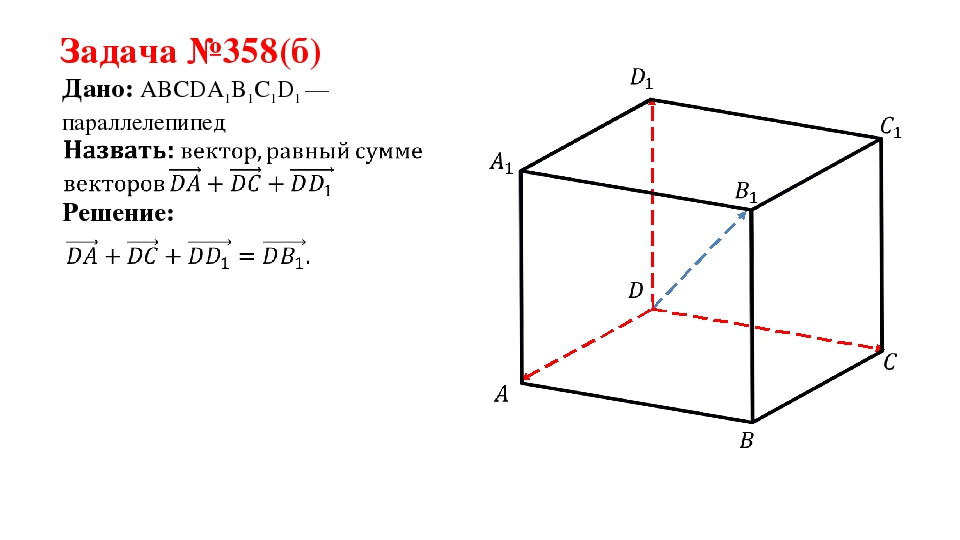
Задача №358(б) Дано: ABCDA1B1C1D1 —параллелепипед Решение:
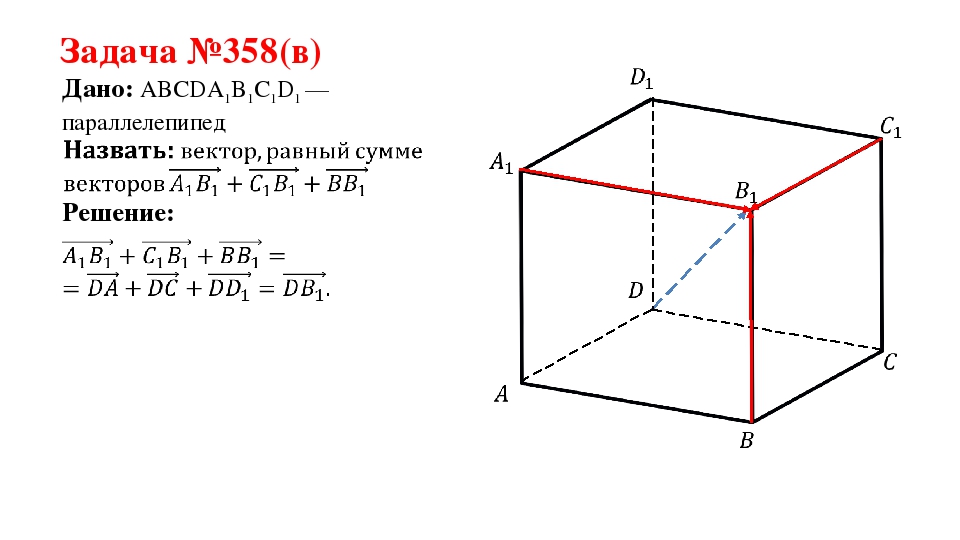
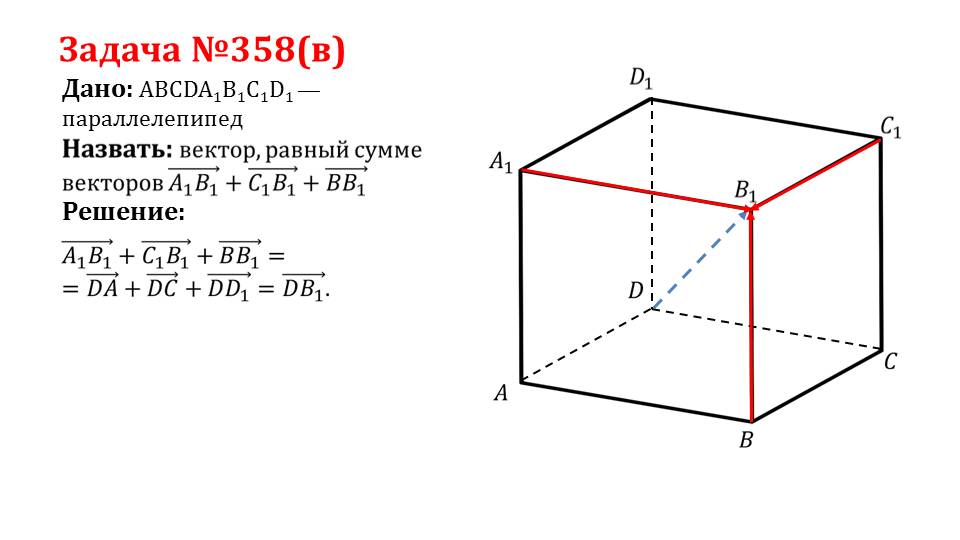
Задача №358(в) Дано: ABCDA1B1C1D1 —параллелепипед Решение:
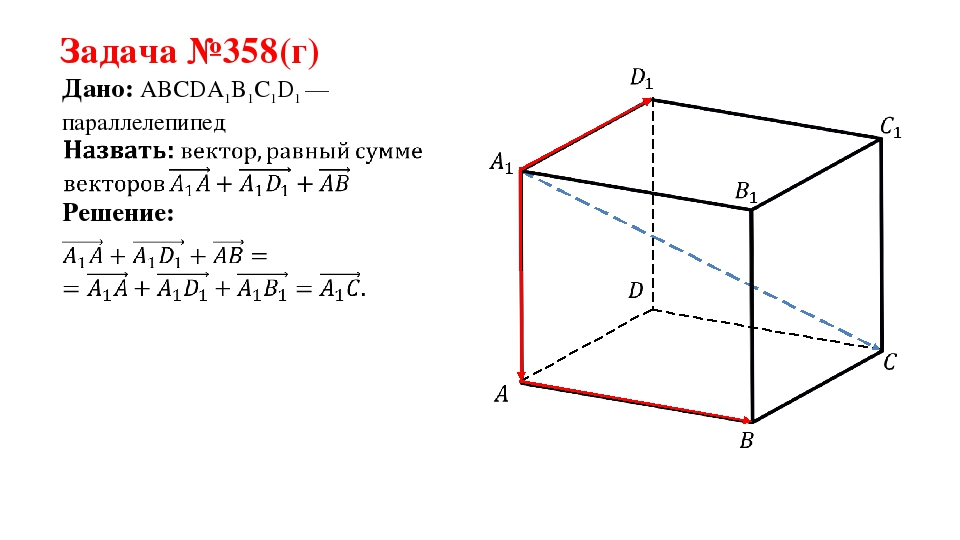
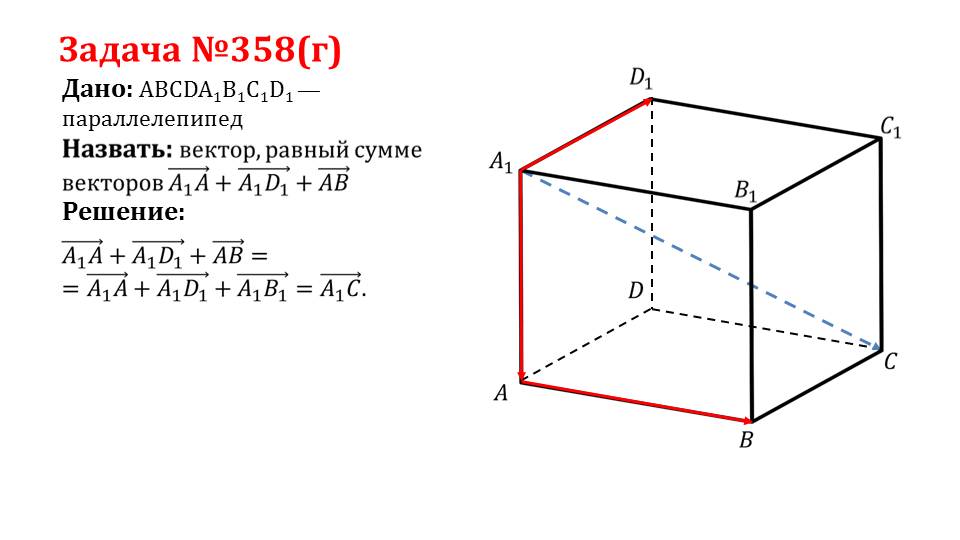
Задача №358(г) Дано: ABCDA1B1C1D1 —параллелепипед Решение:
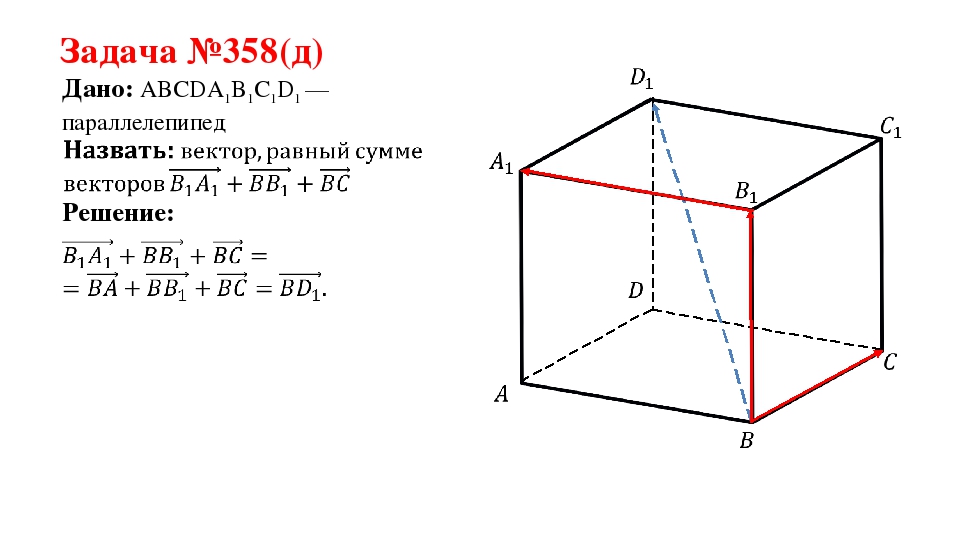
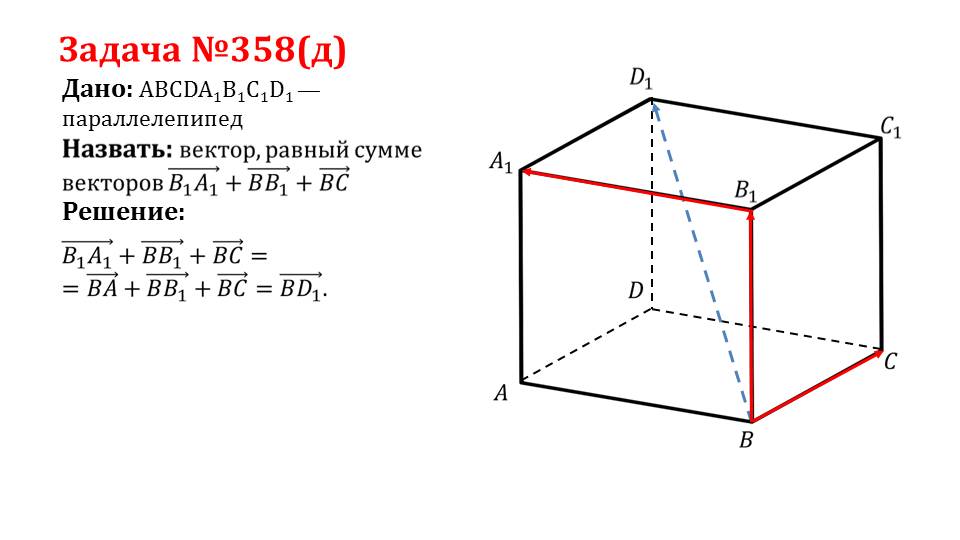
Задача №358(д) Дано: ABCDA1B1C1D1 —параллелепипед Решение:
Краткое описание документа:
Презентация «Правило параллелепипеда» представляет наглядный материал для освоения данной темы на уроке геометрии. Материал урока связывает знания, полученные учениками, о стереометрических телах, а также сведения из векторной алгебры. В ходе презентации ученики получают представление о правиле параллелепипеда, аналогичному правилу параллелограмма на плоскости, затем с помощью описания задач, в которых применяются изученные правила, формируется умение использовать полученные знания на практике.
Презентация решает несколько проблем, которые возникают в ходе изучения темы. С помощью использования наглядного пособия, разнообразия методов ведения урока, применения анимационных эффектов учитель удерживает внимание учеников на изучаемой теме. Также анимационные эффекты и возможность оформления слайдов в различных цветах улучшают представление объемных тел и построений, которые выполняются для рассмотрения их свойств. Благодаря выделению цветом, в построениях отмечаются детали, важные для понимания правила параллелепипеда, способа решения задачи.
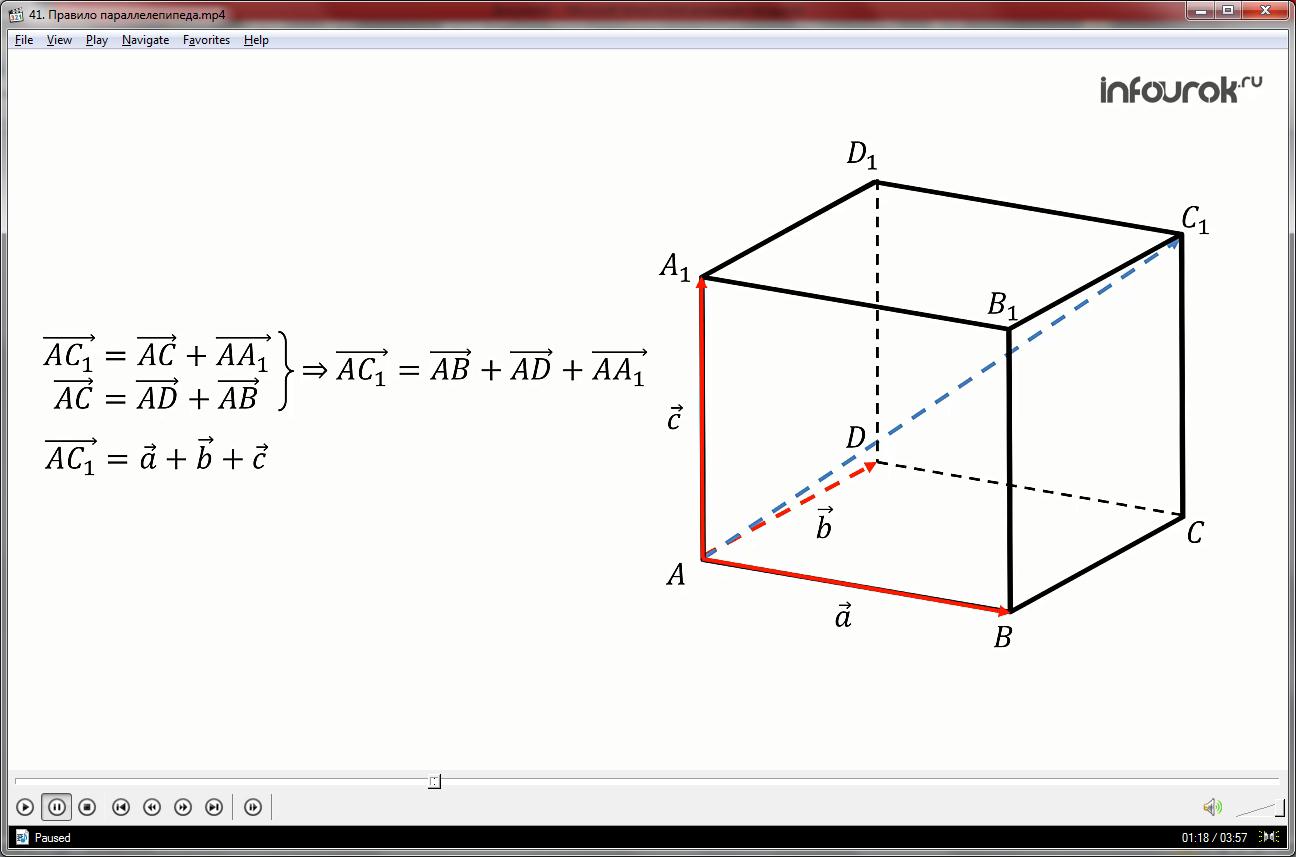
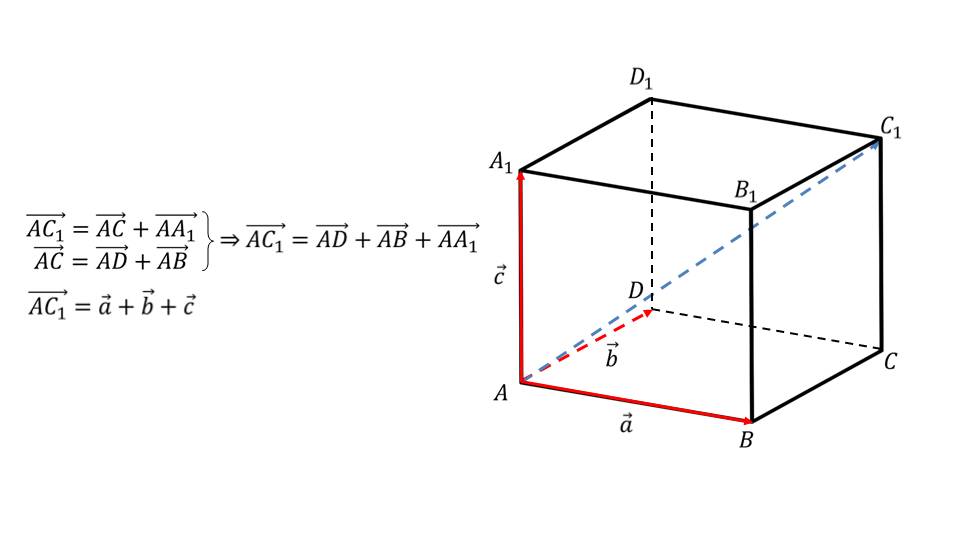
Демонстрация начинается с представления правила параллелепипеда, которое действует для векторов, лежащих в пространстве. Отмечается, что если из вершины параллелепипеда провести по трем его измерениям вектора, то суммарный их вектор будет располагаться на диагонали параллелепипеда. Определение выделено в рамку и рекомендуется для запоминания. Правило также демонстрируется на рисунке, на котором изображен параллелепипед ABCDA1B1C1D1, красным цветом выделены его измерения АВ, AD и AA1, на основе которых строятся векторы aˉ, bˉ, cˉ. Рядом с рисунком обозначены векторы, а также формула, отображающая рассматриваемое правило параллелепипеда AC1ˉ=aˉ+bˉ+cˉ. Описывается доказательство формулы. Используя правило параллелограмма, указываем сумму векторов AC1ˉ= ACˉ+ AА1ˉ, верную для диагональной плоскости AА1СC1, а также сумму векторов АСˉ=ADˉ+ABˉ для плоскости ABCD. Отсюда следует равенство AC1ˉ=ADˉ+ABˉ+AА1ˉ. Иначе данную формулу можно записать AC1ˉ=aˉ+bˉ+cˉ. Теорема доказана.
На слайде 4 описывается решение задачи 358(а). В задаче дан параллелепипед ABCDA1B1C1D1, в котором необходимо назвать вектор, что равен сумме векторов ADˉ+ABˉ+AА1ˉ. Решение сопровождается рисунком, на котором изображен параллелепипед ABCDA1B1C1D1, в котором красным цветом выделены измерения, на которых строятся векторы. Пользуясь правилом параллелепипеда, находим решение задачи ADˉ+ABˉ+AА1ˉ= AC1ˉ. Найденный вектор AC1ˉ отмечен на рисунке синим цветом.
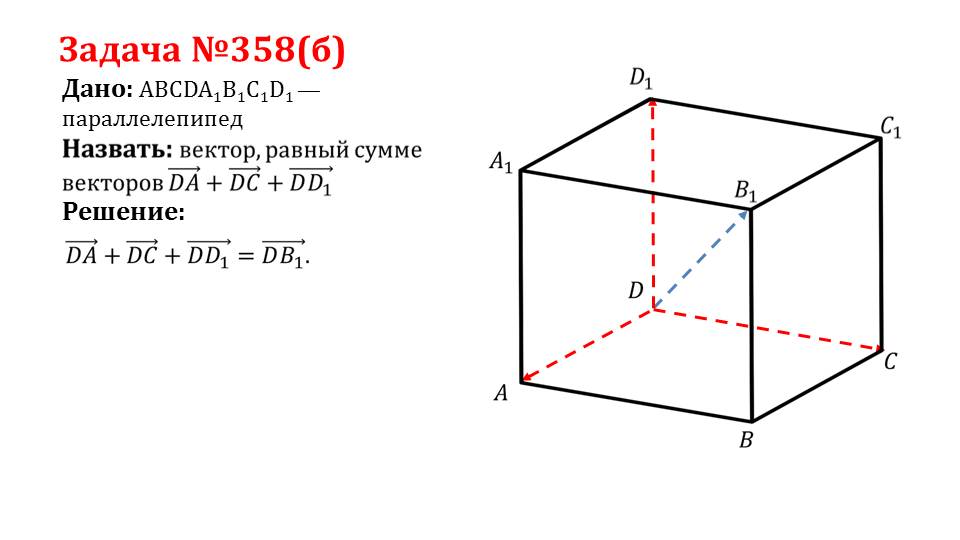
На слайде 5 необходимо найти суммарный вектор векторов DAˉ, DCˉ, DD1ˉ. В решении задачи 358(б) также применяем правило параллелепипеда. Найденный суммарный вектор DAˉ+DCˉ+DD1ˉ= DВ1ˉ.
Следующий слайд демонстрирует решение задачи 358(в), в которой необходимо найти суммарный вектор векторов A1B1ˉ, С1B1ˉ, ВB1ˉ, которые представляют измерения прямоугольного параллелепипеда, сходящиеся в одной вершине. Пользуясь равенством сторон параллелепипеда, можно утверждать, что A1B1ˉ+ С1B1ˉ+ ВB1ˉ=DAˉ+DCˉ+DD1ˉ Очевидно, что при сложении данных векторов образуется вектор диагонали параллелепипеда DВ1ˉ.
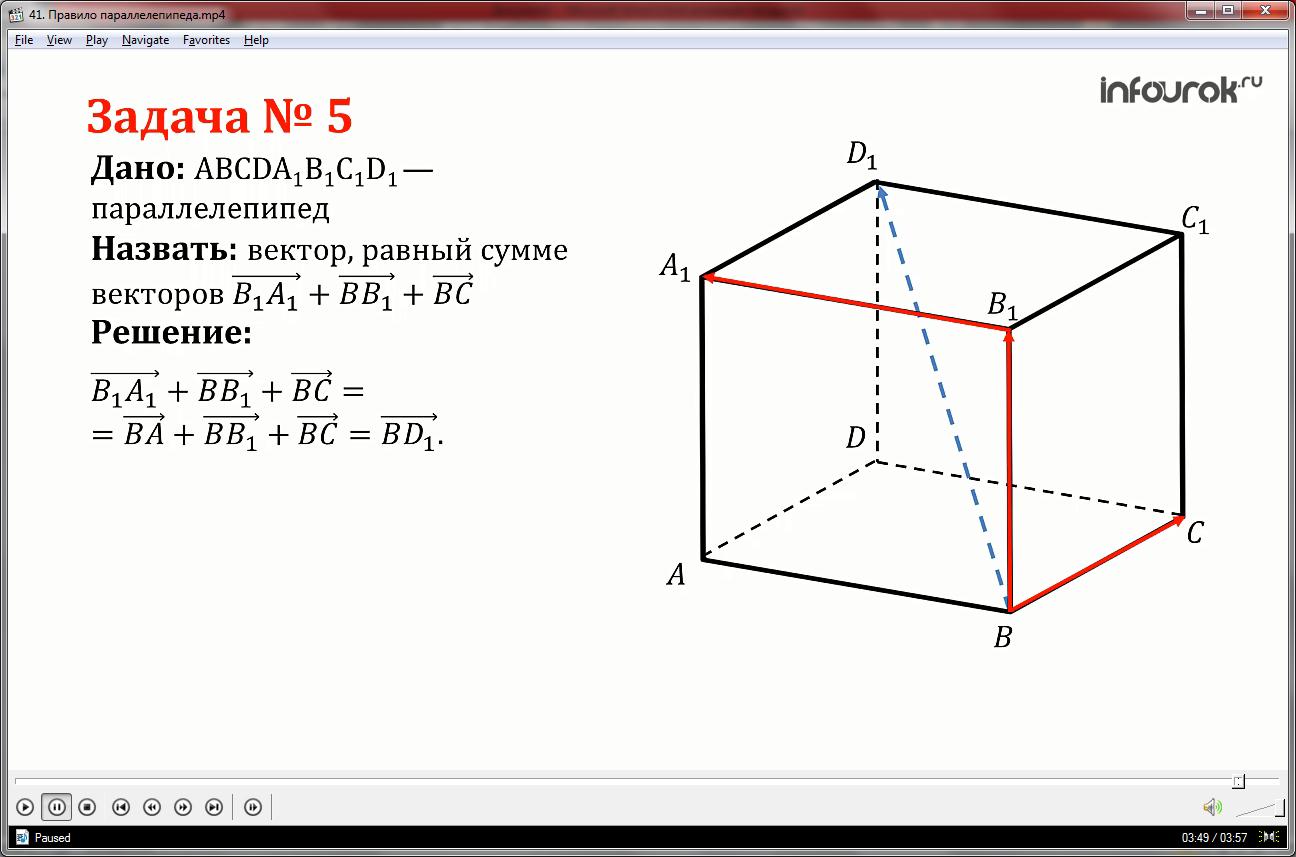
Последний слайд представляет решение задачи 358(д). В задаче дан параллелепипед ABCDA1B1C1D1, в котором необходимоопределить сумму векторов B1A1ˉ, ВB1ˉ, BCˉ. Пользуясь параллельным переносом вектора B1A1ˉ в вершину В, получаем равнозначное выражение для суммы векторов BAˉ+ВB1ˉ+BCˉ. В данном параллелепипеде суммарный вектор является диагональю BD1ˉ. Решение задачи сопровождается рисунком, где выполнено построение параллелепипеда ABCDA1B1C1D1,, красным цветом выделены вектора, над которыми выполняется операция, а также пунктирной линией отмечена суммарная диагональ.
Презентация «Правило параллелепипеда» рекомендуется для использования на традиционном уроке в школе для повышения его эффективности. Материал может подкреплять наглядностью объяснение учителя в ходе дистанционного обучения. Ученики, которым недостаточно урока для глубокого понимания темы, могут использовать презентацию для самостоятельной работы.
Презентация по геометрии «Правило параллелепипеда» (10 класс)
Описание презентации по отдельным слайдам:
Правило параллелепипеда 10 класс МАОУ СОШ № 13 города Тюмени
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1417661
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителя Кубани смогут получить миллион рублей на взнос по ипотеке
Время чтения: 1 минута
В России стартовал прием заявок на конкурс для журналистов-школьников «Медиабум»
Время чтения: 2 минуты
Минобрнауки обновит перечень специальностей высшего образования
Время чтения: 1 минута
Детский омбудсмен предложила обучать педагогов мотивированию учащихся
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Урок «Правило параллелепипеда»
Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Сложение нескольких векторов в пространстве выполняется так: первый вектор складывается со вторым, затем их сумма – с третьим вектором и так далее. Это правило нам известно как правило многоугольника. На рисунке показано сложение трех векторов в пространстве.
От точки О отложен вектор ОА равный вектору а, затем от точки А вектор АВ равный бэ, от точки В отложен следующий вектор ВС равный це, и соединяем первую и последнюю точки О с С получаем вектор ОС равный сумме векторов а, бэ и це.
Сформулируем правило многоугольника.
ЕслиА1, А2, А3 и так далее Аn – произвольные точки, то вектор А1А2 плюс вектор А2А3 плюс вектор А3А4 и так далее плюс Аn-1 An, то в результате получится вектор А1Аn.
На рисунке показана сумма шести векторов.
Если начало вектора совпадает с концом последнего, то сумма равна нулевому вектору.
Рассмотрим сумму векторов
Выполнив сложение по правилу многоугольника, получаем вектор АА или нулевой вектор.
Решим задачу №337 (в)
Решение: Заменим в выражении вычитание на сумму. Для этого заменим отрицательные векторы на противоположные. Вектор минус ВС равен вектору СВ, минус вектор РМ равен вектору МР. Минус вектор АР равен вектору РА. Вектор АС в сумме с вектором СВ дают вектор АВ. Векторы МР и РА дают вектор МА. Затем, складывая векторы АВ и ВМ, получаем вектор АМ. В итоге сумма векторов АМ и МА дают нулевой вектор. Выражение упрощено.
Решим задачу на доказательство №338.
Доказательство. Преобразуем левую часть равенства. Вектор ОА представим как сумму векторов ОА1 и А1А по правилу треугольника. Вектор А1А равен вектору С1С как противоположные ребра параллелепипеда. Складывая векторы ОС1 и С1С, получаем ОС. В результате преобразований получили правую часть равенства. Доказательство окончено.