в чем заключается опыт юнга

В чем заключается опыт юнга

1. Какие два взгляда на природу света существовали с давних пор среди ученых?

До начала XIX в. не было доказательств ни в пользу волновых, ни в пользу корпускулярных представлений.

В настоящее время признана справедливой как волновая, так и корпускулярная теория.
Обе теории, дополняя друг друга, позволяют объяснять многие физические явления.

2. В чем заключалась суть опыта Юнга, что этот опыт доказывал и когда был поставлен?

В 1802 г. английский ученый Томас Юнг поставил опыт по сложению пучков света от двух источников, в результате чего получил не меняющуюся во времени картину, состоящую из чередующихся светлых и темных полос.
Юнг правильно объяснил возникновение полос интерференцией света.

Однако интерференция присуща только волновым (т. е. периодическим) процессам.
Поэтому oпыт Юнга стал доказательством того, что свет обладает волновыми свойствами.

3. В чем заключается интерференция звуковых волн?

При наложении двух когерентных волн (т. е. волн с одинаковой частотой и постоянной разностью фаз) образуется так называемая интерференционная картина, т. е. не меняющаяся со временем картина распределения амплитуд колебаний в пространстве.

В одних точках пространства колебания всегда происходят с максимальной амплитудой.
Это те точки, в которые колебания от обоих источников в любой момент времени приходят в одинаковых фазах и поэтому всегда усиливают друг друга.
В других точках колебания происходят с минимальной амплитудой.
Эти точки расположены по отношению к источникам так, что к ним колебания всегда приходят в противоположных фазах, ослабляя друг друга (а при равных амплитудах колебаний волны в любой момент времени полностью гасят друг друга).
В остальных точках колебания также происходят с постоянными амплитудами, значения которых лежат в промежутке от минимальной до максимальной.

4. Как на опыте можно получить интерференционную картину света?

На проволочное кольцо с ручкой, затянутое мыльной пленкой, в затемненном помещении направляется свет желтого цвета.
На пленке образуются горизонтально расположенные чередующиеся желтые и черные полосы.

5. Как объяснить появление на мыльной пленке чередующихся полос?

Свет, падая на пленку, частично отражается от передней поверхности в точке А, а частично проходит внутрь пленки и отражается от задней поверхности в точке В, после чего выходит из пленки в точке С.
Волны, выходящие из точек A и C, являются когерентными, т,к. они образуются от одного и того же источника.
Разность хода длин волн зависит от толщины пленки, которая в разных точках различна.
Если толщина пленки окажется такой, что волны будут выходить из точек А и С, имея одинаковые фазы, то эти волны при сложении усилят друг друга.
В результате возникнет максимум интерференционной картины — желтая полоса.
Если толщина пленки окажется такой, что волны будут выходить из точек А и С в противоположных фазах, то эти волны при сложении будут гасить друг друга.
В результате возникнет минимум интерференционной картины — темная полоса.

6. Что доказывает опыт с освещением мыльной пленки?

Этот опыт доказывает, что раз наблюдается явление интерференции, значит, свет обладает волновыми свойствами.

7. Что можно сказать о частоте (или длине волны) световых волн разных цветов?

Томас Юнг измерил еще и длину световой волны.
Оказалось, что свету разных цветов соответствуют волны разной длины (разной частоты).

Например, красному свету в световом диапазоне соответствует самая большая длина волны ( иначе самая маленькая частота).
Длины волн убывают (а частоты возрастают) в следующей последовательности цветов: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.

Источник

Интерференция световых волн

Интерференция – это одно из наиболее ярких проявлений волновой природы света. Мы можем наблюдать такое интересное и красивое явление, если наложить друг на друга 2 или более световых пучков. В месте перекрывания пучков интенсивность волны света обладает характером чередующихся светлых и темных полос, при этом в точках максимумов интенсивность больше, а в точках минимумов меньше суммы интенсивностей пучков.

При белом свете интерференционные полосы окрашиваются в разные цвета светового спектра. На практике интерференционные явления окружают нас повсюду. Это и цвета масляных пятен на асфальте, и окрашивание замерзающих оконных стекол, и чудесные цветные рисунки на крыльях отдельных бабочек и жуков.

Первый научный эксперимент проявления интерференции света

Интерференционный опыт Юнга

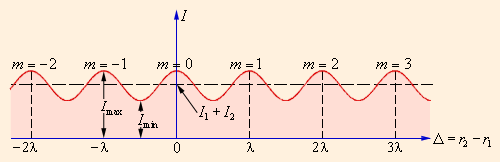
Путем простых тригонометрических вычислений можно прийти к следующему выражению для интенсивности результирующего колебания в точке P :

где Δ = r 2 – r 1 – это разность хода.

Подчеркнем, что в волновой оптике понятие “луч света” теряет физический смысл в отличие от геометрической оптики. Определение «луч» в волновой оптике употребляется для краткости обозначения направления распространения волны.

Далее данный термин будет упоминаться без кавычек.

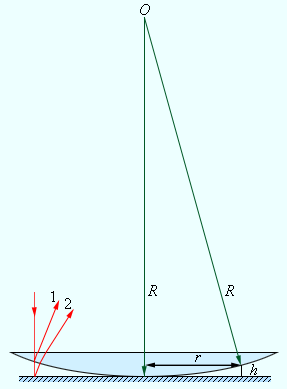
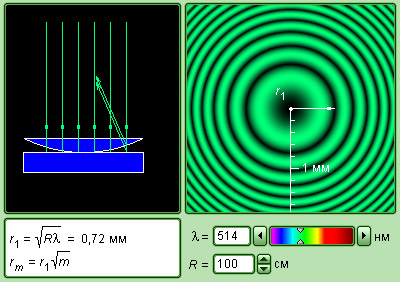
По данной формуле рассчитывается длина световой волны λ при известном радиусе кривизны R линзы.

Проблема когерентности волн

Источник

В чем заключается опыт юнга

Как было уже показано, для наблюдения интерференции света необходимо иметь когерентные световые пучки, для чего применяются различные приёмы. В опыте Юнга когерентные пучки получали разделением и последующим сведением световых лучей, исходящих из одного и того же источника (метод деления волнового фронта).

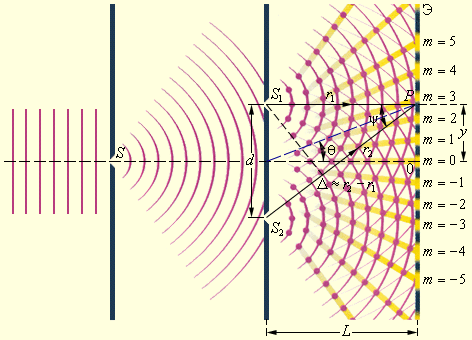
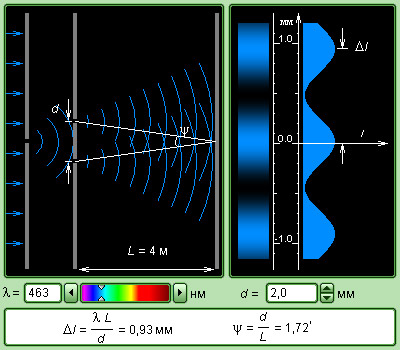
Рассмотрим интерференционную картину, полученную методом Юнга (рис. 8.2).

Свет от источника S, прошедший через узкую щель в экране А, падет на экран В с двумя щелями S₁ и S₂, расположенными достаточно близко друг к другу на расстоянии d. Эти щели являются когерентными источниками света. Интерференция наблюдается в области, в которой перекрываются волны от этих источников (поле интерференции). На экране Э мы видим чередование полос с максимумом и минимумом интенсивности света.

Экран расположен на расстоянии l от щелей, причем .

Рассмотрим две световые волны, исходящие из точечных источников S₁ и S₂. Показатель преломления среды – n.

Вычислим ширину полос интерференции (темных и светлых полос).

Интенсивность в произвольной точке P экрана, лежащей на расстоянии x от О, определяется (для вакуума, когда n = 1) оптической разностью хода .

; ,

отсюда , или

.

Из условия следует, что , поэтому

Отсюда получим, что максимумы интенсивности будут наблюдаться в случае, если

а минимумы – в случае, если

Расстояние между двумя соседними максимумами (или минимумами) равно:

и не зависит от порядка интерференции (величины m) и является постоянной для данных l, d.

Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между соседними минимумами – шириной интерференционной полосы.

Т.к. обратно пропорционально d, при большом расстоянии между источниками, например при , отдельные полосы становятся неразличимыми, сравнимыми с длиной волны . Поэтому необходимо выполнять условие .

Этот опыт показывает, что интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос. Главный максимум, соответствующий , проходит через точку О. Вверх и вниз от него располагаются максимумы (минимумы) первого ( ), второго ( ) порядков и т. д.

Из перечисленных формул видно, что ширина интерференционной полосы и расстояние между ними зависят от длины волны λ. Только в центре картины при совпадут максимумы всех волн. По мере удаления от центра максимумы разных цветов смещаются друг относительно друга все больше и больше. Это приводит, при наблюдении в белом свете, ко все большему размытию интерференционных полос. Интерференционная картина будет окрашенной, но нечеткой (смазанной).

Измерив , зная l и d, можно вычислить длину волны λ. Именно так вычисляют длины волн разных цветов в спектроскопии.

Источник

Опыт Юнга может перевернуть наше представление о реальности.

Популярные материалы

Today’s:

Опыт Юнга может перевернуть наше представление о реальности.

Традиционный эксперимент в области физики может скрывать в себе знания о природе реальности, о которых мы и не догадывались. Классический опыт юнга, известный также как «Эксперимент на Двух Щелях», в свое время стал доказательством волновой теории света. Но на самом деле он бросает вызов одному из самых известных и изученных предположений квантовой механики.

Дисперсия света

Каждый из нас когда-нибудь видел, как переливаются лучи на граненых изделиях из стекла или, например, на бриллиантах. Наблюдать это можно благодаря такому явлению, как дисперсия света. Это эффект, отражающий зависимость показателя преломления предмета (вещества, среды) от длины (частоты) световой волны, которая проходит через этот предмет. Следствием такой зависимости является разложение луча на цветовой спектр, например, при прохождении через призму. Дисперсия света выражается следующим равенством:

где n – показатель преломления, ƛ – частота, а ƒ – длина волны. Показатель преломления увеличивается с ростом частоты и уменьшением длины волны. Дисперсию мы нередко наблюдаем в природе. Самым красивым ее проявлением является радуга, которая образуется благодаря рассеиванию солнечных лучей при прохождении их через многочисленные капли дождя.

Опыт Юнга с конвертами. Вопрос о квантовом стирании данных

Зеркало Ллойда

Дифракционная решетка. Определение и основные сведения о дифракционной решетке

Дифракционной решеткой называют спектральный прибор, который является системой некоторого количества щелей, разделенных непрозрачными промежутками.

Очень часто на практике используют одномерную дифракционную решетку, состоящую из параллельных щелей одинаковой ширины, находящихся в одной плоскости, которые разделяют равными по ширине непрозрачными промежутками. Такую решетку изготавливают при помощи специальной делительной машины, которая наносит на пластине из стекла параллельные штрихи. Количество таких штрихов может быть более чем тысяча на один миллиметр.

Лучшими считаются отражательные дифракционные решетки. Это совокупность участков, которые отражают свет с участками, которые свет отражают. Такие решетки представляют собой отшлифованную металлическую пластину, на которой рассеивающие свет штрихи нанесены резцом.

Картина дифракции на решетке — это результат взаимной интерференции волн, которые идут ото всех щелей. Следовательно, при помощи дифракционной решетки реализуется многолучевая интерференция когерентных пучков света, которые подверглись дифракции и которые идут от всех щелей.

Допустим, что на дифракционной решетке ширина щели будет a, ширина непрозрачного участка — b, тогда величина:

называется периодом (постоянной) дифракционной решетки.

Видео Опыт Юнга с Двумя щелями. Рус. Хорошее качество.

Опыт Юнга с двумя щелями. Опыт Юнга или эксперемент с двумя щелями

В опыте пучок света направляется на непрозрачный экран-ширму с двумя параллельными прорезями, позади которого устанавливается проекционный экран. Особенность прорезей в том, что их ширина приблизительно равна длине волны излучаемого света (влияние ширины прорезей на интерференцию рассматривается ниже). На проекционном экране получается целый ряд чередующихся интерференционных полос, что и было продемонстрировано Томасом Юнгом.

На проекционном экране получается целый ряд чередующихся интерференционных полос, что и было продемонстрировано Томасом Юнгом.
Если исходить из того, что свет состоит из частиц (корпускулярная теория света), то на проекционном экране можно было бы увидеть только две параллельные полосы света, прошедшие через прорези ширмы. Между ними проекционный экран оставался бы практически неосвещенным.
С другой стороны, если предположить, что свет представляет собой распространяющиеся волны (волновая теория света), то, согласно принципу Гюйгенса, каждая прорезь является источником вторичных волн.
Если вторичные волны достигнут линии в середине проекционного экрана, находящейся на равном удалении от прорезей, в одной фазе, то на серединной линии экрана их амплитуды сложатся, что создаст максимум яркости. То есть, максимум яркости окажется там, где, согласно корпускулярной теории, яркость должна быть практически нулевой.
С другой стороны, на определённом удалении от центральной линии волны окажутся в противофазе — их амплитуды компенсируются, что создаст минимум яркости (тёмная полоса). По мере дальнейшего удаления от средней линии яркость периодически изменяется, возрастая до максимума и снова убывая.

Интерференционная картина возникает на экране, когда ширина прорезей близка к длине волны излучаемого монохроматического света. Если ширину прорезей увеличивать, то освещённость экрана будет возрастать, но контраст интерференционной картины будет падать вплоть до полного её исчезновения.

Интерференция света.

Сложение волн. Очень часто в среде одновременно распространяется несколько различных волн. Например, когда в комнате беседуют несколько человек, то звуковые волны накладываются друг на друга. Что при этом происходит?

Проще всего проследить за наложением механических волн, наблюдая волны на поверхности воды. Если мы бросим в воду два камня, создав этим две кольцевые волны, то нетрудно заметить, что каждая волна проходит сквозь другую и ведет себя в дальнейшем так, как будто бы другой волны совсем не существовало. Точно так же любое число звуковых волн может одновременно распространяться в воздухе, ничуть не мешая друг другу. Множество музыкальных инструментов в оркестре или голосов в хоре создают звуковые волны, одновременно улавливаемые нашим ухом. Причем ухо в состоянии отличить один звук от другого.

Теперь посмотрим более внимательно, что происходит в местах, где волны накладываются друг на друга. Наблюдая волны на поверхности воды от двух брошенных в воду камней, можно заметить, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если две волны встречаются в одном месте гребнями, то в этом месте возмущение поверхности воды усиливается.

Если же, напротив, гребень одной волны встречается с впадиной другой, то поверхность воды не будет возмущена.

Вообще же в каждой точке среды колебания, вызванные двумя волнами, просто складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую (т. е. с учетом их знаков) сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.

Интерференция. Сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний, называется интерференцией.
Выясним, при каких условиях имеет место интерференция волн. Для этого рассмотрим более подробно сложение волн, образуемых на поверхности воды.

Результат сложения волн, приходящих в точку M, зависит от разности фаз между ними. Пройдя различные расстояния d1и d2, волны имеют разность хода Δd = d2—d1. Если разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой ровно на один период (как раз за период волна проходит путь, равный длине волны). Следовательно, в этом случае гребни (как и впадины) обеих волн совпадают.

Условие максимумов. На рисунке 120 изображена зависимость от времени смещений X1и X2, вызванных двумя волнами при Δd= λ. Разность фаз колебаний равна нулю (или, что то же самое, 2л, так как период синуса равен 2п). В результате сложения этих колебаний возникает результирующее колебание с удвоенной амплитудой. Колебания результирующего смещения на рисунке показаны цветом (пунктир). То же самое будет происходить, если на отрезке Δd укладывается не одна, а любое целое число длин волн.

Амплитуда колебаний среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн:

Условие минимумов. Пусть теперь на отрезке Δd укладывается половина длины волны. Очевидно, что при этом вторая волна отстает от первой на половину периода. Разность фаз оказывается равной п, т. е. колебания будут происходить в противофазе. В результате сложения этих колебаний амплитуда результирующего колебания равна нулю, т. е. в рассматриваемой точке колебаний нет (рис. 121). То же самое произойдет, если на отрезке укладывается любое нечетное число полуволн.
Амплитуда колебаний среды в данной точке минимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна нечетному числу полуволн:

Зеркала Френеля

S — точечный источник света;
Z1, Z2 — зеркала;
S1, S2 — мнимые изображения источника света;
E — экран;
D — область перекрытия потоков света от мнимых источников, где наблюдается интерференция;
B — бленда для защиты от засветки экрана источником света.
Для наглядности угол между зеркалами на рисунке утрированно увеличен.

Опыты, проведённые с этим прибором явились одним из решающих доказательств волновой природы света.

Источник