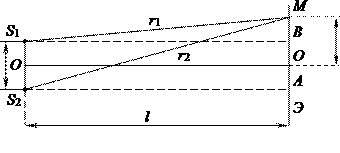в чем заключается метод юнга по разделению светового пучка
В чем заключается метод юнга по разделению светового пучка
Как было уже показано, для наблюдения интерференции света необходимо иметь когерентные световые пучки, для чего применяются различные приёмы. В опыте Юнга когерентные пучки получали разделением и последующим сведением световых лучей, исходящих из одного и того же источника (метод деления волнового фронта).
Рассмотрим интерференционную картину, полученную методом Юнга (рис. 8.2).
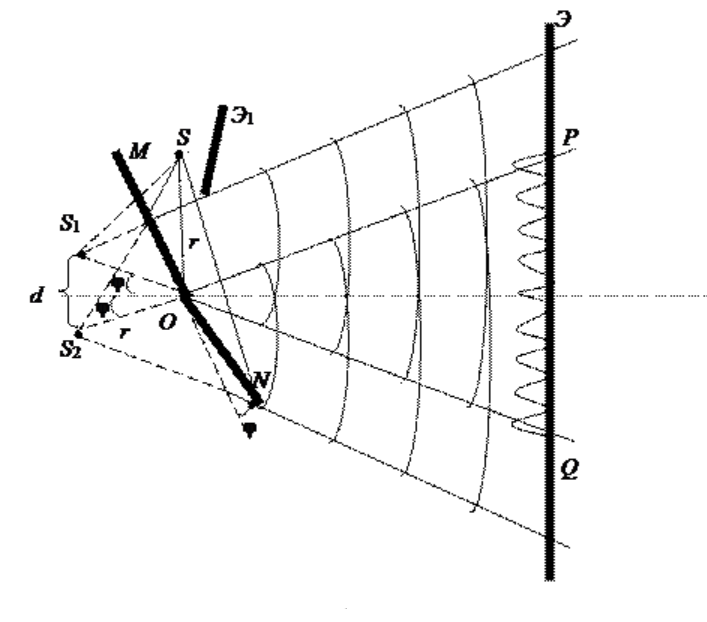
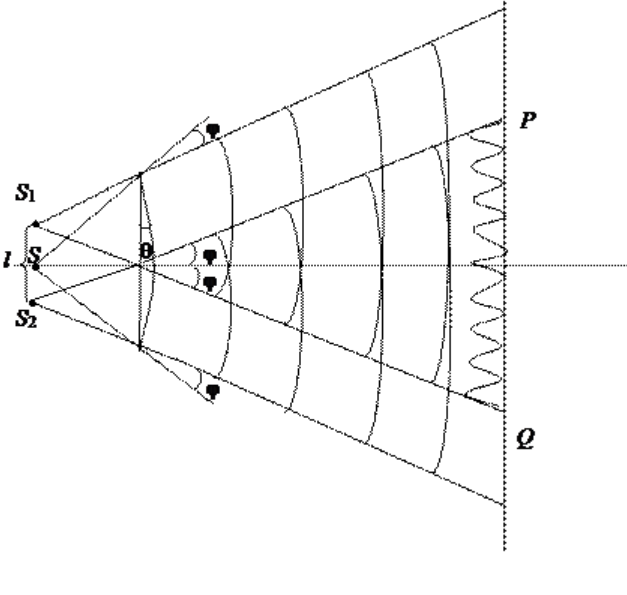
Свет от источника S, прошедший через узкую щель в экране А, падет на экран В с двумя щелями S1 и S2, расположенными достаточно близко друг к другу на расстоянии d. Эти щели являются когерентными источниками света. Интерференция наблюдается в области, в которой перекрываются волны от этих источников (поле интерференции). На экране Э мы видим чередование полос с максимумом и минимумом интенсивности света.
Экран расположен на расстоянии l от щелей, причем 
.
Рассмотрим две световые волны, исходящие из точечных источников S1 и S2. Показатель преломления среды – n.
Вычислим ширину полос интерференции (темных и светлых полос).
Интенсивность в произвольной точке P экрана, лежащей на расстоянии x от О, определяется (для вакуума, когда n = 1) оптической разностью хода 
.
; 
,
отсюда 
, или
.
Из условия следует, что 
, поэтому
Отсюда получим, что максимумы интенсивности будут наблюдаться в случае, если
а минимумы – в случае, если
Расстояние между двумя соседними максимумами (или минимумами) равно:
и не зависит от порядка интерференции (величины m) и является постоянной для данных l, d.
Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между соседними минимумами – шириной интерференционной полосы.
Т.к. 
обратно пропорционально d, при большом расстоянии между источниками, например при 
, отдельные полосы становятся неразличимыми, сравнимыми с длиной волны 
. Поэтому необходимо выполнять условие .
Этот опыт показывает, что интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос. Главный максимум, соответствующий 
, проходит через точку О. Вверх и вниз от него располагаются максимумы (минимумы) первого ( 
), второго ( 
) порядков и т. д.
Из перечисленных формул видно, что ширина интерференционной полосы и расстояние между ними зависят от длины волны λ. Только в центре картины при 
совпадут максимумы всех волн. По мере удаления от центра максимумы разных цветов смещаются друг относительно друга все больше и больше. Это приводит, при наблюдении в белом свете, ко все большему размытию интерференционных полос. Интерференционная картина будет окрашенной, но нечеткой (смазанной).
Измерив , зная l и d, можно вычислить длину волны λ. Именно так вычисляют длины волн разных цветов в спектроскопии.
В чем заключается метод юнга по разделению светового пучка
1. Какие два взгляда на природу света существовали с давних пор среди ученых?
До начала XIX в. не было доказательств ни в пользу волновых, ни в пользу корпускулярных представлений.
В настоящее время признана справедливой как волновая, так и корпускулярная теория.
Обе теории, дополняя друг друга, позволяют объяснять многие физические явления.
2. В чем заключалась суть опыта Юнга, что этот опыт доказывал и когда был поставлен?
В 1802 г. английский ученый Томас Юнг поставил опыт по сложению пучков света от двух источников, в результате чего получил не меняющуюся во времени картину, состоящую из чередующихся светлых и темных полос.
Юнг правильно объяснил возникновение полос интерференцией света.
Однако интерференция присуща только волновым (т. е. периодическим) процессам.
Поэтому oпыт Юнга стал доказательством того, что свет обладает волновыми свойствами.
3. В чем заключается интерференция звуковых волн?
При наложении двух когерентных волн (т. е. волн с одинаковой частотой и постоянной разностью фаз) образуется так называемая интерференционная картина, т. е. не меняющаяся со временем картина распределения амплитуд колебаний в пространстве.
В одних точках пространства колебания всегда происходят с максимальной амплитудой.
Это те точки, в которые колебания от обоих источников в любой момент времени приходят в одинаковых фазах и поэтому всегда усиливают друг друга.
В других точках колебания происходят с минимальной амплитудой.
Эти точки расположены по отношению к источникам так, что к ним колебания всегда приходят в противоположных фазах, ослабляя друг друга (а при равных амплитудах колебаний волны в любой момент времени полностью гасят друг друга).
В остальных точках колебания также происходят с постоянными амплитудами, значения которых лежат в промежутке от минимальной до максимальной.
4. Как на опыте можно получить интерференционную картину света?
На проволочное кольцо с ручкой, затянутое мыльной пленкой, в затемненном помещении направляется свет желтого цвета.
На пленке образуются горизонтально расположенные чередующиеся желтые и черные полосы.
5. Как объяснить появление на мыльной пленке чередующихся полос?
Свет, падая на пленку, частично отражается от передней поверхности в точке А, а частично проходит внутрь пленки и отражается от задней поверхности в точке В, после чего выходит из пленки в точке С.
Волны, выходящие из точек A и C, являются когерентными, т,к. они образуются от одного и того же источника.
Разность хода длин волн зависит от толщины пленки, которая в разных точках различна.
Если толщина пленки окажется такой, что волны будут выходить из точек А и С, имея одинаковые фазы, то эти волны при сложении усилят друг друга.
В результате возникнет максимум интерференционной картины — желтая полоса.
Если толщина пленки окажется такой, что волны будут выходить из точек А и С в противоположных фазах, то эти волны при сложении будут гасить друг друга.
В результате возникнет минимум интерференционной картины — темная полоса.
6. Что доказывает опыт с освещением мыльной пленки?
Этот опыт доказывает, что раз наблюдается явление интерференции, значит, свет обладает волновыми свойствами.
7. Что можно сказать о частоте (или длине волны) световых волн разных цветов?
Томас Юнг измерил еще и длину световой волны.
Оказалось, что свету разных цветов соответствуют волны разной длины (разной частоты).
Например, красному свету в световом диапазоне соответствует самая большая длина волны ( иначе самая маленькая частота).
Длины волн убывают (а частоты возрастают) в следующей последовательности цветов: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.
Опыт Юнга может перевернуть наше представление о реальности
Суть эксперимента заключается в том, что на непрозрачный экран-ширму с двумя параллельными прорезями, позади которого установлен другой, проекционный экран, направляют пучок света. Особенность прорезей заключается в том, что их ширина приблизительно равна длине волны излучаемого света. Логично было бы предположить, что фотоны должны проходить сквозь щели, создавая две параллельные полосы света на заднем экране. Но вместо этого свет распространяется в виде полос, в которых чередуются участки света и темноты, то есть свет ведет себя как волна. Это явление называется « интерференция», и именно его демонстрация Томасом Юнгом стала доказательством справедливости волновой теории. Переосмысление этого эксперимента могло бы объединить квантовую механику с другой опорой теоретической физики, общей теорией относительности Энштейна, — вызов, который до сих пор остается неразрешимым на практике.
Для того, чтобы вычислить вероятность появления фотона в том или ином месте на экране, физики используют принцип под названием «правило Борна». Тем не менее, для этого нет никаких причин — эксперимент всегда проходит одинаково, но никто не знает почему. Некоторые энтузиасты пытались объяснить этот феномен из интерпретации квантово-механической теории о «множественных мирах», в которой предполагается, что все возможные состояния квантовой системы могут существовать в параллельных вселенных, но эти попытки ни к чему не привели.
Это обстоятельство позволяет использовать правило Борна как доказательство наличия в квантовой теории нестыковок. Для того, чтобы объединить квантовую механику, которая оперирует Вселенной в узких временных масштабах, и общую теорию относительности, которая работает с огромными промежутками времени, одна из теорий должна уступить дорогу. Если же правило Борна неверно, то это будет первый шаг к изучению квантовой гравитации. «Если правило Борна будет нарушено, что будет нарушена и фундаментальная аксиома квантовой механики, и мы узнаем, где следует искать ответ на теории о квантовой гравитации», говорит Джеймс Куотч из Института науки и техники в Испании.
Куотч предложил новый способ проверить правило Борна. Он исходил из идеи физика Фейнмана: для того, чтобы вычислить вероятность возникновения частицы в той или иной точке экрана, вы должны учитывать все возможные пути, по которым это может произойти, даже если они кажутся смешными. «Учитывается даже та вероятность, что частица долетит до Луны и вернется обратно», говорит Куотч. Практически ни один из путей не повлияет на окончательное местоположение фотона, но некоторые, весьма необычные, могут в конечном итоге изменить его координаты. К примеру предположим, что у нас есть три пути, благодаря которым частица может пролететь сквозь экран, вместо двух очевидных (т.е. вместо той или иной щели). Правило Борна в этом случае позволяет рассматривать помехи, которые могут возникнуть между двумя очевидными вариантами, но не между всеми тремя.
Джеймс показал, что, если учитывать все возможные отклонения, то итоговая вероятность того, что фотон угодит в точку Х, будет отличаться от результата, который предполагает правило Борна. Он предложил использовать в качестве третьего пути блуждающий зигзаг: так, частица проходит сначала сквозь левое отверстие, затем сквозь правое, и лишь затем направляется к экрану. Если третий путь препятствует первым двум — изменится и результат вычислений. Работа Куотча вызвала большой интерес, и Анинда Синха в Индийском институте науки в Бангалоре — член команды, которая впервые предложила использовать для опровержения правила Борна извилистые, «нетрадиционные» пути, — с ней полностью согласен. Однако ученый указывает и на то, что существует слишком много неучтенных вероятностей, чтобы сейчас можно было говорить о чистоте эксперимента. Как бы то ни было, результаты этой работы откроют человечеству дверь в область более глубокого понимания реальности.
Основные интерференционные схемы
Для интерференции света необходимым условием является получение когерентных световых пучков. В процессе его выполнения, свое применение находят различные приемы. До того времени, когда во всех приборах для наблюдения интерференции света появились лазеры, когерентные пучки получали с помощью разделения и последующего сведения световых лучей, испускаемым одним и тем же источником. На практике, это может быть осуществимо при помощи экранов и щелей, зеркал и преломляющих тел. Разберем некоторые из таких методов.
Метод Юнга и интерференция света
Зеркала Френеля
Бипризма Френеля
Пара изготовленных из одного куска стекла призм с мизерным преломляющим углом q обладают одной общей гранью и называются бипризмой Френеля (рис. 3 ).
Область, в которой волны накладываются друг на друга, носит название поля интерференции.
Во всей этой области наблюдается чередование мест с максимальной и минимальной интенсивностью света. Если в поле интерференции поместить экран, то на нем будет проявляться интерференционная картина, выражающаяся в виде чередования светлых и темных полос.
Определим оптическую разность хода между когерентными волнами, распространяющимися от источников S 1 и S 2 в приведенную точку M на экране. Точка M размещена на расстоянии x от центра интерференционной картины.
где L 2 = r 2 n и L 1 = r 1 n представляют собой оптические длины пути для первой и второй волн, а r 2 и r 1 – геометрические длины пути первой и второй волн.
Для случая треугольников S 1 А М и S 2 В М будет справедливой следующая запись:
Оптическая разность ход будет эквивалентна выражению:
Расстояние между двумя соседними максимумами (или минимумами), порядок m которых отличается на единицу, определяется как ширина интерференционной полосы.
Опыт Юнга с квантовой точки зрения
Юнг, проковыряв две маленькие дырочки в непроницаемом для света экране, задал задачу науке не разрешимую до сих пор. Лучшие умы мировой науки (Фейнман, Пенроуз и множество других наших и не наших столпов) никак не поймут, почему так не логично ведут себя частицы и волны при проходе через эти две злополучные дырочки Юнга. К сожалению, в рамках атомарного уровня познания это понять вообще невозможно, сколько не бейся. Надо перейти на квантовый уровень, на 20 порядков ниже.
И опыт то вроде простой. Ну не сравнишь же его с коллайдером. Приходится констатировать:
Загадочный эксперимент в области квантовой физики, результаты которого современная наука не может объяснить.
Прямо беда какая-то.
Вот классическая схема эксперимента. Рисунок 1.
S – источник света (у Юнга это обычный солнечный свет),
A – диафрагма с отверстием (у Юнга это оконная штора с небольшим отверстием),
B – непрозрачная пластина с отверстиями,
S1 и S2 – небольшие отверстия или щели в пластине,
И тут начинаются чудеса. Когда открыта только одна щель, на экране видна одна светлая полоса. Открывая вторую щель, мы надеемся получить вторую светлую полосу. Но не тут то было. Вместо двух полос мы видим три, а то и больше полос. На рисунке их пять. Все зависит от качества опыта. Причем оказывается, что расстояние между горбами кривой освещенности Δx для различных цветов различное.
Мало того средняя светлая полоса иногда оказывается прямо между отверстиями, куда свет по логике вещей вообще не должен попадать. А он попадает. Юнг смекнул, что свет имеет волновую структуру, и волны из двух щелей создают на экране интерференционную картинку. Примерно так:
Роджер Пенроуз в своей книге “Новый ум короля” тоже нарисовал примерно такую же картинку. Рисунок 6.7.
И по поводу этой картинки он высказал такие мысли.
Нет ничего загадочного в поведении обычной макроскопической классической волны, проходящей одновременно через две щели. Волна в конечном счете представляет собой всего лишь “возмущение” либо некоторой непрерывной среды (поля), либо некоторого вещества, состоящего из мириад крохотных точечных частиц.
Интересно, какие поля имеет в виду Пенроуз? Думаю, что кроме магнитного, электрического, электромагнитного, гравитационного и, может быть, торсионного полей, нам ничего найти не удастся. Может быть он хочет возвратится к эфиру или какому-нибудь особому вакууму? Что из этого было в комнате Юнга? Это эти поля интерферировали в его опытах? Похоже, что – нет.
Но в корпускулярной картине ситуация иная: каждый отдельный фотон сам по себе ведет себя, как волна! Ибо, если значительно уменьшить полную интенсивность света, то можно гарантировать, что вблизи щелей будет находиться не более одного фотона одновременно.
А один фотон – это что частица, ведущая себя как волна? Что – это какая-то летящая со скоростью света частица и все время раздувающаяся, как шар? Причем поверхность этого шара должна колебаться с соответствующей частотой. Или частица летит до щелей, не выказывая своих волновых свойств? И когда она и при каких условиях вдруг обнаружит, что ей надо развернутся до плоской волны? Практически шару с бесконечным радиусом. Какая-то несуразица.
В самом деле фотон и есть то вещество, как пишет Пенроуз, состоящее из мириад крохотных точечных частиц, то есть одиночных элементарных фотонов. Естественно, что элементарные фотоны мы измерять не можем. Это сверхзадача для человечества. Конечно же, элементарный фотон не может создать и интерференционную картинку. Это компактные вихри, которые не обладают свойством увеличения или превращения в какой-то синусоидальный вид.
Пенроуз делает верно, когда сравнивает размер фотона с размерами щели и расстоянием между щелями. Он пишет:
Если в качестве “размера” фотона принять его длину волны, то в масштабе фотона вторая щель находится от первой на расстоянии около 300 “размеров фотона” (а ширина каждой щели составляет около двух длин волн фотона).
Фотон никак не может одновременно контактировать с двумя щелями и поэтому у Пенроуза возникает вопрос:
Каким образом фотон, проходя через одну из щелей, “узнает” о том, открыта или закрыта другая щель?
На самом деле, в принципе не существует предела для расстояния, на которое могут быть разнесены щели, для того, чтобы произошло явление “гашения или усиления”.
А вот тут не так. Длина фотона в данном случае не имеет никакого значения. В щель пролезают элементарные фотоны, а не фотон целиком. Как генерируется фотон. Увеличим сильно нить накаливания лампочки.
При подаче на проводник напряжения электроны придут в движение и излучат фотоны, которые и полетят в этом же порядке в пространство. Если, например, электрон а задержит фотон один, то фотон 1 задержится, но сечение фотона, то есть вектор Пойтинга, останется прежним. Вот такая и будет толщина фотона. Конечно, это идеальная картинка излучения фотона. На самом деле фотоны будут излучаться во все стороны от проводника. В этом повинна и форма проводника, и тепловое движение, и отражения, и преломления и тому подобное. Диаграмма излучения будет шарообразной. Это мы видим на практике.
Единственное что, к сожалению, мы не видим это то, что этот шар будет полый. Пока напряжение U будет возрастать, до тех пор и будут излучаться фотоны. Как только напряжение поменяет знак, ускорение прекратится, электроны будут двигаться по инерции и ничего излучать не будут. Вот этот, будем считать шарообразный, слой фотонов и отправится в путешествие от излучателя. Он улетит на некоторое расстояние от источника и за ним ничего не будет, пока электроны в проводнике не затормозятся обратным напряжением и не загрузятся новыми фотонами. Затем напряжение снова поменяет знак и начнет ускорять электроны, и они снова излучать новую волну фотонов. Расстояние между этими порциями энергии и есть длина волны излучения.
Фотоны, составляющие эти кольца или какие-нибудь другие фигуры в сечении, в идеале будут выглядеть примерно так:
Таким образом, мы перед щелями мы всегда имеем волну “некоторого вещества, состоящего из мириад крохотных точечных частиц” по выражению Пенроуза.
Эти крохотные точечные частицы не что иное, как фотоны и они не точечные, а линейные, что чрезвычайно важно. Хотите, называйте их струнами или стрелочками Фейнмана. Каждый из элементарных фотонов проходит только через одну щель, и знать не знает и не желает знать, открыта вторая щель или закрыта. Природа делает свое дело.
Для элементарного фотона щель представляется тоннелем с торчащими со всех сторон атомами со своими электронами. Чем уже щель, тем труднее проскользнуть фотону не про взаимодействовав с каким-нибудь электроном. А взаимодействие всегда приводит к изменению направления фотона. Это приводит к тому, что на выходе щели получается рассеянное полусферическое кольцо. Если исходную волну мы считаем почти плоской, то на выходе щели – это сферическая волна. В ней элементарные фотоны частично перемешались, развернулись и сдвинулись.
И теперь самое главное. В этих волнах кажется полный беспорядок в элементарных фотонах. Тот фотон короткий, тот длинный, а тот еще длиннее. Все они беспорядочно сдвинуты по фазе в каждой волне. Как они могут усиливать или погашать друг друга, по выражению Пенроуза?
Современная наука приучила нас к тому, чтобы мы складывали синусоиды с учетом фаз. Но синусоиды – это виртуальные объекты и поэтому для них существуют свои виртуальные законы. А природа работает с объективно существующими импульсом и энергией фотона. И сумматору (электрону) в больших пределах безразлично, когда начнут на него воздействовать фотоны. Примерно так, как качелям безразлично, когда три человека передадут им свой импульс, лишь бы это случилось на восходящей или нисходящей ветви. То есть, когда качели находятся вверху и начали двигаться в низ, то один человек их может толкнуть сразу же, другой где-то в средине, а третий в нижней точке. А могут толкнуть все три одновременно. Если импульсы одинаковы, то и результат будет одинаков.
С фотонами такая же ситуация. Если два фотона оказались на каком-то электроне даже со сдвигом один относительно другого, то они могут сложиться на электроне и затем излучится в виде этой суммы.
Рассмотрим увеличенный до атомов участок экрана. Конечно, это идеализирована схема. На данный участок падают фотоны со щели 1 (красные стрелочки) и фотоны со второй щели (голубые стрелочки). В зависимости от расстояния от щелей фотоны прибывают к одному и тому же атому в различное время. Допустим фотон из щели 1 попал на электрон 1 в точке а орбиты электрона. Импульс фотона будет тормозить электрон. Если фотон не излучился до точки б и в это время на этот же электрон попадет фотон со второй щели, то этот фотон будет ускорять электрон. То есть один фотон тормозил электрон, а второй ускорял электрон. Электрон согласно этой сумме сил приобретет какую-то скорость. И соответственно этой скорости излучит или поглотит фотон.
На электроне 1 произойдет вычитание фотонов. На электроне 2 тоже произойдет вычитание фотонов. На электроне 3 может произойти как вычитание, так и сложение. А на электронах 4, 5, 6 произойдет сложение фотонов. Так по всей плоскости экрана и будет идти волной вычитание и сложение. В идеальном случае, результатами вычитания и сложения фотонов могут быть фотоны различной длины, от нулевой, до суммы квантов в обоих фотонах. Если ни один из результатов не будет резонансным для данного электрона, то электрон излучит эту сумму. Так как частоты этих излученных фотонов совпадают с частотой падающих фотонов, то это будет тот же цвет, только различной интенсивности. Появляются полосы различной интенсивности.
Если, например, экраном будет светочувствительная пластина, то суммарные фотоны определенной величины переведут атомы серебра на другие уровни. А суммарные фотоны меньше этой величины излучатся атомами, и атомы останутся в прежнем состоянии. На пластине будут светлые и темные полосы.
Сбивает с толку ученый люд и такое явление. Как быть с частицами? Они ведь тоже создают интерференционную картинку. Да, создают. Наверное, многие видели мультик, как дедушка в очках палит из пушки электронами по двум щелям и получает интерференционную картинку. Ему невдомек, что когда он палит из пушки, то ускоряет электроны, которые генерируют фотоны. А эти фотоны и создают данную картинку.
Если бы на экране скапливались в полосе электроны, то их потенциал можно было бы легко измерить. На светлой полосе один потенциал, а на темной полосе другой и все споры прекратились бы. И уж совсем невозможно представить, как электроны в светлых полосах нейтрализуют друг друга.
Но кроме этого возникает еще одна проблема с частицами. Когда мы пытаемся увидеть частицу, то есть проводим измерения, на одной щели, то интерференция прекращается. Очевидно, что мы вмешались в движение, чем изменили параметры движения этой частицы, и она вышла из интерференционного процесса. Фейнман определил интерференцию, как проход частицы через обе щели. По его теории, например, электрон одновременно движется по множественным путям к своему пункту назначения. До щели он летал, обходя все препоны и ловушки, и вдруг после щели попал в наш измерительный прибор. Не смог, имея в своем арсенале множество путей распространения, обойти наш прибор. Проведите тысячи измерений, и результат будет тот же.
В общем можно сказать, что никакого дуализма в том понятии, как представляют его себе ученые, нет. А тем более возводить это несуразное, не подчиняющееся никакой логике, понятие в закон квантовой механики и вовсе нелепо.
Дуализм существует только в таком виде. Фотон состоит из вихрей полей, назовите это волнами, а фотоны, движущиеся друг за другом с определенной скважностью (частотой излучения), представляют волну. Волна не материальна, она организатор материальных частиц в движение, которое мы называем волной.