в чем заключается метод стокса
Как определить вязкость жидкости методом Стокса?
Формулу определения вязкости Стокс вывел ещё в 1851 году.
Он получил выражение, описывающее действие силы трения (лобового сопротивления) на круглый объект, движущийся в вязкой жидкости с небольшим числом Рейнольдса.
Чтобы понять, как определять вязкость жидкости методом Стокса необходимо узнать теоретическое описание процесса, вывод формулы и сам описание самого метода.
Всё это и конкретные методы описаны далее в статье.
Содержание статьи
Что такое вязкость
Сама по себе вязкость это свойство жидкости сопротивляться сдвигу слоев. Такой сдвиг выражается в том, что при относительном перемещении слоёв жидкости тот слой, что движется медленнее тормозит слой, который движется быстрее и наоборот.
Вязкость проявляется в наличии между молекулами жидкости сил притяжения, которые пытаются сдерживать движение слоев при перемещении одной части жидкости относительно другой.
По природе все жидкости являются вязкими, потому что между молекулами существуют силы притяжения и отталкивания. Если один слой жидкости вывести из равновесия и сдвигать его относительно другого с некоторой скоростью, то силы взаимного притяжения молекул будут пытаться тормозить это движение.
Движение тела в жидкой среде
Когда твердое тело попадает в жидкость, оно сталкивается с некоторым сопротивлением. Происхождение сил сопротивления жидкости в этом случае может быть объяснено двумя разными механизмами.
Если скорость движения твердого тела маленькая и за ним не образовывается завихрений, то силы сопротивления жидкости характеризуются только вязкостью.
В таком случае слои жидкости, которые прилегают к этому твердому телу, движутся вместе с ним. Но слои жидкости, граничащие с первыми слоями, тоже приходят в движения из-за сил молекулярного притяжения (сцепления).
Таким образом образуются силы, которые затормаживают относительное движение твердого тела в жидкости.
Завихрения вокруг твердого тела образуются из-за различия скоростей движения жидкости перед телом и за ним. При этом давление в стационарном потоке жидкости изменяется таким образом, что в области вихрей оно существенном меньше.
Разность давлений в областях перед твердым телом и за ним создает противоположную по направлению движения силу лобового сопротивления жидкости. Эта сила тормозит движение твердого тела.
Сила сопротивления
В случае, когда движение твердого тела в жидкости происходит без образования вихрей, т.е. медленно, сила сопротивления образуется по первому из двух описанных механизмов.
Для тел круглой формы, согласно формуле Стокса, сила сопротивления будет равна:
где μ – вязкость жидкости;
r – радиус шарика;
υ – скорость равномерного движения шарика.
Условие использования формулы
Существует несколько ограничений для применения формулы Стокса.
1. вязкая среда не ограничена стенками и находится в покое
2. скольжений на границах с твердым телом нет
3. движение жидкости ламинарное
4. радиус круглого тела намного больше, чем длина среднего пробега молекул жидкой среды
Формула вязкости
Рассмотрим конкретный случай, когда на шар, движущийся в жидкости действуют три силы:
FT – сила тяжести;
FA – сила Архимеда (выталкивающая сила);
TC – сила лобового сопротивления.
Для круглого шарика сила тяжести будет:
где r –радиус шара;
ρ – плотность шара;
ρ0 – плотность жидкости;
g – ускорение свободного падения;
υ – скорость равномерного движения шарика;
μ – вязкость жидкости.
В жидкости выталкивающая сила и сила тяжести постоянны. Сила лобового сопротивления пропорциональна скорости движения шарика и на первых этапах она существенно меньше силы тяжести.
При дальнейшем движении шарика наступает момент, когда все три силы уравновешиваются и тогда:
или подставляя формулы
таким образом, определение коэффициента вязкости жидкости методом Стокса сводится к формуле
Определение вязкости методом Стокса
Для того чтобы определить вязкость методом Стокса используют высокий сосуд цилиндрической формы.
На сосуд наносят метки А и В. Такие метки располагаются на заведомо известном расстоянии l друг от друга.
Затем в сосуд наливают исследуемую жидкость выше верхней метки А на 4 – 5 сантиметров. Это необходимо для того, чтобы во время прохождения шариком первой метки его скорость можно было считать установившейся.
Далее шарик бросают в сосуд и секундомером определяют время за которое он проход расстояние от метки А до метки В.
Учитывая, что скорость это отношения длины пути ко времени, т.е.:
и заменяя радиус шарика его диаметром d и определяет коэффициент вязкости жидкости методом стокса
Указанная выше формула применимо в тех случаях, когда шар падает в безграничной среде. Если он падает вдоль оси трубки диаметром R0 (как в этом случае) необходимо ввести поправки на радиус сосуда.
При падении шара радиусом r в трубе радиусом R0 и высотой h формула будет выглядеть
Исходя из всего вышесказанного получаем, что определение вязкости жидкости методом Стокса требует значения таких параметров, как:
плотность материала шарика;
плотность жидкости;
радиус шарика;
радиус сосуда;
скорость движения шарика.
Видео про методы определения вязкости
Вязкость – это важная характеристика жидкой среды. Её необходимо учитывать при перекачке жидкостей и газов по трубопроводам, смазке машин и механизмов, разливке расплавленных металлов.
Для определения вязкости используют специальные приборы вискозиметры и специальные методы определения. Каждый из методов определения вязкости характеризуется своим набором условий применения.
Но независимо от метода общими остаются:
1. результат измерение не должен зависеть от линейных размеров вискозиметра.
2. не должно быть пристеночного скольжения жидкости.
3. поток жидкости в используемом вискозиметре должен быть ламинарным.
Определение вязкости жидкости методом Стокса
Цель работы:изучение движения тела в вязкой жидкости и определение динамического коэффициента вязкости.
Приборы и принадлежности:сосуд с глицерином, шарики (дробинки), микрометр, ареометр, линейка, секундомер.
Описание установки и теоретическое обоснование метода.
Стокс исследовал движение маленького шарика в вязкой жидкости. При малых скоростях шарика сила лобового сопротивления пропорциональна скорости.
Точный теоретический расчет, выполненный Стоксом, мы опускаем, а запишем, что сила сопротивления для сферического тела:
(14)
Формула (14) выражает закон Стокса, определяющий силу сопротивления шарика при его медленном равномерном движении в вязкой бесконечно распространенной среде.
Этот закон применяют при определении скоростей оседания мелкодисперсных частиц в различных жидких и газовых средах (осаждение коллоидных частиц, дым, туман, оседание эритроцитов и т.д.).
На применении закона Стокса основан данный метод определения вязкости различных сред. Для этой цели в стеклянный цилиндрический сосуд высотой более 0,8 м наливают исследуемую жидкость и наблюдают в ней свободное падение небольшого металлического шарика. (дробинки)
Условия опыта:
1. По отношению к размерам шарика среда должна быть бесконечно распространенной.
2. Движение шарика в среде должно быть равномерным.
3. Обтекание шарика жидкостью должно носить ламинарный характер.
Первое условие выполняется, если диаметр шарика много меньше диаметра сосуда. Для достижения равномерного движения шарика необходимо, чтобы результирующая всех сил, действующих на него во время движения, была равна 0.
Движение шарика в вязкой среде происходит под действием трех сил: силы тяжести 
, силы гидростатического выталкивания (Архимедовой силы ) 
и силы сопротивления среды 
(рис. 5.)
 |
Две силы ( и ) при движении не изменяются и равны:
(15); 
(16)
Величина силы сопротивления FC следует из формулы Стокса (формула 14).
С ростом скорости сила сопротивления F жидкости движению шарика увеличится, поэтому при достижении шариком некоторой скорости u сумма сил и уравновешивает силу тяжести (рис. 5) и движение станет равномерным. Искомая скорость находится из условия Р = FA + FC, откуда скорость равна:
, (17)
а вязкость жидкости равна:
(18)
Опыты заключаются в измерении времени t прохождения шариком высоты h между двумя визирами на цилиндре. Начальное положение уровня жидкости должно быть выше верхнего визира на 10-15 см, чтобы на контрольном участке движение шарика стало равномерным.
Тогда скорость движения шарика будет u = h/t и вязкость найдем по формуле:
(19).
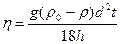
Практическая часть
Задание: определить динамическую вязкость глицерина.
Ход работы:
1. С помощью ареометра измерить плотность исследуемой жидкости.
2. Измерить микрометром диаметр шарика. (дробинки).
3. Смочить шарик глицерином и опустить в сосуд.
4. Замерить секундомером время t прохождения шариком высоты h.
6. Вычислить среднее арифметическое значение вязкости глицерина и его погрешность, считая результаты опытов малыми выборками.
7. Записать окончательный результат для доверительной вероятности
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра физики
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА
Методические указания к лабораторной работе №8
по физике
УДК 530.1
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА: Метод. указания.- Ростов н/Д: Издательский центр ДГТУ, 2010.- 10с
Указания содержат краткое описание явления внутреннего трения и метода определения коэффициента вязкости (динамического) жидкости.
Методические указания предназначены для студентов инженерных специальностей всех форм обучения, в программу учебного курса которых входит выполнение лабораторных работ по физике (раздел >).
Печатается по решению методической комиссии факультета
Рецензент доцент каф. физики, к. ф.-м. н. ЛЕМЕШКО Г. Ф.
©Издательский центр ДГТУ, 2010
Лабораторная работа №8
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА
Цель работы: Познакомиться со способом определения коэффициента вязкости жидкости методом Стокса.
Оборудование: Стеклянный цилиндр с исследуемой жидкостью, измерительная шкала с миллиметровыми делениями, микрометр, секундомер, набор металлических шариков.
Явлениями переноса в термодинамически неравновесных системах называются особые необратимые процессы, в результате которых происходит пространственный перенос энергии либо массы, или импульса. К явлениям переноса относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса).
Внутреннее трение (вязкость)
Сила внутреннего трения между двумя слоями жидкости (газа) определяется по закону Ньютона:
(1)
где 
— коэффициент динамической вязкости, коэффициент пропорциональности,
— градиент скорости (градиентом скорости называется изменение скорости 
на единицу длины 
в направлении, перпендикулярном скоростям v1 и v2 (рис.1),
– площадь слоя, на который действует сила 
.
В системе СИ единица измерения 
:
Из (1) получаем: 
равен динамической вязкости среды, в которой при ламинарном течении и градиенте скорости с модулем, равным 1 м/с на 1м, возникает сила внутреннего трения 1 Н на 1м2 поверхности касания слоев.
Исходя из основных представлений молекулярно-кинетической теории, коэффициент вязкости газов равен:
, (2)
где 
– плотность газа, 
— средняя длина свободного пробега молекул, 
— (3)
средняя скорость движения молекул (здесь 
-универсальная газовая постоянная, 
— термодинамическая температура, 
-молярная масса газа).
Из (2) и (3) следует, что коэффициент вязкости газов возрастает с увеличением температуры. Динамический коэффициент вязкости жидкостей примерно в 104 раз больше, чем у газов и уменьшается с возрастанием температуры.
Описание метода и установки для определения коэффициента вязкости
Установка для определения коэффициента вязкости состоит из высокого цилиндрического сосуда, наполненного исследуемой жидкостью (см. рис. 2).
Метод Стокса основан на определении скорости медленно движущихся в жидкости тел сферической формы. Рассмотрим падение тела (в нашем случае – металлического шарика) в вязкой покоящейся жидкости. На тело действуют следующие силы:
Сила тяжести, направленная вертикально вниз:
, (4),
где 
— радиус шарика, 
– плотность материала шарика, 
— ускорение свободного падения.
Сила Архимеда, направленная вертикально вверх:
, (5)
где Vш – объем шарика, 
– плотность жидкости,
Сила сопротивления (эмпирически установленная
Дж. Стоксом), направленная вертикально Рис.2 вверх:
, (6)
где v – скорость падения тела.
Выражение (6) справедливо при обтекании тела жидкостью (газом) без образования вихрей.
Направление сил показано на рис 2.
При движении тела в жидкости, ее молекулы взаимодействуют с молекулами тела. За счет действия межмолекулярных сил в процесс движения вовлекаются соседние молекулы жидкости. Появляется слой жидкости, движущийся вместе с телом со скоростью движения тела. Этот слой увлекает в своем движении соседние слои жидкости, которые на некоторый период времени приходят в плавное безвихревое движение (случай малых скоростей и малых размеров тела).
Вначале скорость движения тела будет возрастать, так как сила тяжести больше суммы сил сопротивления и силы Архимеда.
По второму закону Ньютона:
(7)
По мере увеличения скорости тела сила сопротивления будет также возрастать, наступит такой момент, когда сила тяжести 
уравновесится суммой сил 
и 
, т. е. можно считать, что тело падает с постоянной скоростью. Ускорение станет равным нулю и формула (7) с учетом (4), (5), (6) запишется так:
. (8)
Учитывая, что скорость тела постоянна и равна:
, (9),
(10)
Выражение (10) справедливо лишь при условии d >)
Редактор
В печать
Объем Офсет. Формат
Бумага тип № Заказ № Тираж Цена
Издательский центр ДГТУ
Адрес университета и полиграфического предприятия:
Описание метода Стокса
 | — плотность материала шарика |
 | — плотность жидкости |
| m | — масса шарика |
| V | — объем шарика |
| r | — радиус шарика |
| v | — скорость движения шарика в жидкости |
| g | — ускорение силы тяжести |
| h | — высота жидкости в цилиндре |
| R | — радиус цилиндра |
На движущийся в жидкости шарик действует сила внутреннего трения, тормозящая его движение. При условии, что стенки сосуда находятся далеко от шарика, эта сила по закону Стокса определяется формулой (3). Если шарик свободно падает в вязкой жидкости, то на него будут действовать также сила тяжести 
и выталкивающая сила Архимеда 
.
На основании 2-го закона динамики Ньютона имеем:
(4).
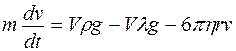
Решением полученного уравнения является закон изменения скорости шарика с течением времени при его падении в жидкости:
(5).
Поскольку с течением времени величина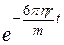 
очень быстро убывает, то скорость шарика вначале возрастает (рис.2). Но через малый промежуток времени становится величиной постоянной, равной: 
(6), где 
.
Скорость шарика можно определить, зная расстояние 
между метками на сосуде и время t, за которое шарик проходит это расстояние: 
.
Подставив эти равенства в (6), выразим из него коэффициент вязкости:
Получаем окончательно рабочую расчетную формулу для экспериментального определения коэффициента вязкости жидкости методом Стокса:
(8)
1. Какие силы действуют на падающий в жидкости шарик? Каковы характер и динамика его движения?
2. Записать формулу закона Стокса и пояснить входящие в нее обозначения?
3. Каковы условия применимости закона Стокса? Как они учтены в работе?
4. Записать расчетную формулу для вязкости жидкости? Пояснить каким образом находятся значения входящих в нее величин в данной работе.
5. Чем обусловлено положение верхней метки на цилиндрическом сосуде по отношению к краю жидкости в нем?
6. Пояснить характер зависимости скорости шарика [формула (5)] по рис.2.
7. От чего зависит получаемое значение вязкости? Каковы источники возможных погрешностей результата?
Содержание экспериментальных заданий.
Задание 1. Вычисление расстояния релаксации.
1) Выбрать шарик наибольшего радиуса и измерить его диаметр, массу, вычислить объем и среднюю плотность.
2) Измерить линейкой расстояние d от поверхности масла в цилиндрическом сосуде до верхней отметки.
3) По справочной таблице найти значение плотности и коэффициента вязкости касторового масла, записать в тетрадь.
4) По формуле (6) рассчитать скорость 
равномерного падения шарика.
5) На основе формулы (5) найти минимальное время 
, соответствующее значению скорости, найденному в предыдущем пункте.
6) Интегрированием формулы (5) в пределах от t=0 до t=tр вычислить путь S, проходимый шариком при его неравномерном движении в жидкости.
7) Сравнить полученное значение S с расстоянием d от поверхности жидкости в сосуде до верхней метки. Сделать соответствующий вывод о применимости расчетной формулы.
Задание 2. Экспериментальное определение вязкости касторового масла.
1) Взять 3 металлических шарика (стальные или свинцовые) и микрометром произвести несколько измерений их диаметров. Вычислить средние значения радиусов данных шариков. Занести эти и последующие результаты в таблицу.
2) Свободно отпустить шарик в исследуемую жидкость и засечь время 
прохождения им расстояния между метками. Проделать это для каждого из взятых шариков, i =1, 2, 3.
3) Измерить расстояние между метками и записать какова абсолютная погрешность этого значения 
.
4) Определить температуру исследуемой жидкости (температуру воздуха в помещении).
5) Для каждого опыта вычислить по расчетной формуле полученное значение вязкости. Найти его среднее значение и сравнить с табличным.
6) Сделать вывод о правильности проведенного эксперимента и пояснить возможные причины расхождения теоретического и экспериментального значений коэффициента вязкости касторового масла.
7) Оценить погрешность результат проделанного измерения как косвенного многократного измерения. Записать ответ в форме 
, 
(степень доверия Р=. ).
Задание 3. Исследование зависимости скорости падения шарика в вязкой жидкости.
1) Подставьте полученные в ходе выполнения эксперимента числовые значения соответствующих величин в формулу (5) и запишите ее вид после проведения соответствующих вычислений (возьмите данные, соответствующие падению одного из шариков).
2) Постройте на миллиметровой бумаге график зависимости скорости падения шарика от времени падения с указанием выбранных масштабов. Точный график можно построить в системе Mathcad на компьютере.
3) Сравните значение скорости равномерного движения шарика, полученное из графика с тем, что было посчитано в ходе опыта.
4) По графику определить время , через которое скорость шарика перестанет меняться. Посчитать площадь фигуры под графиком на участке от начала движения до 
. Сравнить эту величину с расстоянием d от поверхности жидкости в сосуде по верхней метки.
5) Сделайте необходимый вывод.
Вопросы к отчету:
1. Поясните сущность явления вязкого трения. Какова природа сил внутреннего трения жидкости?
2. Сформулируйте закон Ньютона и поясните входящие в него величины.
3. Что такое коэффициент вязкости?
4. Запишите формулу Стокса и укажите условия ее применимости. Докажите справедливость формулы (3) методом размерностей.
5. Какое движение жидкости называют ламинарным? Запишите условие ламинарности.
6. Выведите формулу зависимости скорости падения шарика от времени из динамического уравнения его движения в вязкой жидкости.
7. Сформулируйте утверждения, отражающие основные результаты данного эксперимента.
8. Перечислить основные источники погрешностей измерений, проводимых в данной работе. Как они были вами учтены при оценке точности результата?
Лабораторная работа № 1.4.
Определение модуля Юнга металлической проволоки.
Цель работы: познакомиться с числовыми характеристиками и законами упругой продольной деформации твердых тел; исследовать упругие свойства металла, в частности на практике изучить деформацию растяжения на примере металлической проволоки; познакомиться с методом экспериментального нахождения модуля Юнга.
Приборы и принадлежности: нихромовая или стальная проволока, закрепленная с одного конца, грузы и подвесная опора для них, два микроскопа с окулярными шкалами, микрометр, масштабная линейка.