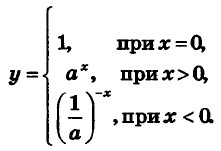в чем заключается метод последовательного уточнения при построении алгоритма
05. Метод последовательного уточнения
Снизу вверх
| Похоже на манипуляции с детским конструктором: из элементарных деталей сначала собираются простые блоки, из них более сложные, и в конце концов из больших блоков получается (или не получается) задуманная юным конструктором машинка. |
Однако, далеко не всегда этот метод результативен. Нередко при переходе на очередной уровень выясняется, что написанные на предыдущих этапах процедуры совершенно бесполезны при составлении очередного алгоритма. Сокрушаясь по поводу зря потраченного времени, приходится возвращаться к нижнему уровню и начинать сначала.
Сверху вниз (МПУ)
Чтобы понять, какие процедуры действительно необходимы для решения задачи, а потом описывать только их, достаточно начать с общего плана. Этот план одновременно является и главным алгоритмом, а его пункты именами будущих процедур. Таким образом выясняются не только имена процедур, но и порядок, в котором их надо вызывать.
На следующем этапе можно переходить к уточнению отдельных пунктов общего плана, т.е. к написанию вспомогательных алгоритмов. Здесь можно применить тот же прием: сразу приступать к сотавлению процедуры, заменяя все предписания, которых нет в СКИ, вызовами новых вспомогательных алгоритмов.
Понятно, что на каждом этапе придется последовательно уточнять пункты плана возникшего на предыдущем уровне. И так до тех пор, пока на самом нижнем уровне не получатся процедуры, состоящие только из команд, входящих в СКИ. Это и есть метод последовательного уточнения.
| Представьте юного конструктора, котрый, перед тем как начать малопредсказуемую деятельность по соединению деталей, решается набросать рисунок будущего чуда техники, затем чертежи его основных блоков, потом частей этих блоков и так до тех пор, пока не будет совершенно ясно, как эти мелкие части получаются из элементарных деталей конструктора. |
Итак, метод последовательного уточнения состоит в следующем:
Пример решения задачи
Если суть метода понятна, можно попробовать решить ЗАДАЧУ:
Попробуем записать эту идею (план)
в виде основного алгоритма лес :
Если очередная подзадача оказывается достаточно простой, мы можем, не прибегая к дальнейшей декомпозиции, решить ее сразу. Для этого надо в соответствующем алгоритме использовать только команды из СКИ (не прибегая к вызовам еще не написанных вспомогательных алгоритмов).
Дальнейшее уточнение этого алгоритма уже не требутся, т.к. все используемые команды «понятны» исполнителю.
Аналогичным образом можно уточнить все остальные алгоритмы и, тем самым, завершить решение задачи.
Замечания
Все-таки есть подозрение, что даже в этом случае с помощью метода последовательного уточнения получатся более короткие, с ясной структурой, легко проверяемые алгоритмы (главный и вспомогательные).
Да, их (вспомогательных), наверное, будет побольше.
Но, во-первых, меньше вероятность, что при их написании будут допущены ошибки,
а, во-вторых, если все-же ошибки будут, их быстрее можно будет найти и исправить,
благодаря четкой структуре получившейся программы.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 2.3. Конструирование алгоритмов
Информатика. 9 класса. Босова Л.Л. Оглавление
Ключевые слова:
Последовательное построение алгоритма
Существуют различные методы конструирования (разработки, построения) алгоритмов. Мы познакомимся с одним из них — методом последовательного построения (уточнения) алгоритма. Иначе он называется методом разработки «сверху вниз», нисходящим методом или методом пошаговой детализации.
Процесс последовательного построения алгоритма выглядит следующим образом.
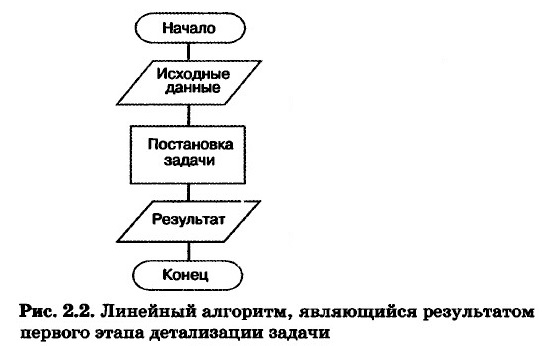
На первом шаге мы считаем, что перед нами совершенный исполнитель, который «всё знает и всё умеет». Поэтому достаточно определить исходные данные и результаты алгоритма, а сам алгоритм представить в виде единого предписания — постановки задачи (рис. 2.2).
Если исполнитель не обучен исполнять заданное предписание, то необходимо представить это предписание в виде совокупности более простых предписании (команд). Для этого:
Процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.
Объединяя полученные предписания в единую совокупность выполняемых в определённой последовательности команд, получаем требуемый алгоритм решения исходной задачи.
Разработка алгоритма методом последовательного уточнения для исполнителя Робот
Вы уже знакомы с исполнителем Робот. Он действует на клетчатом поле, между клетками которого могут быть стены.
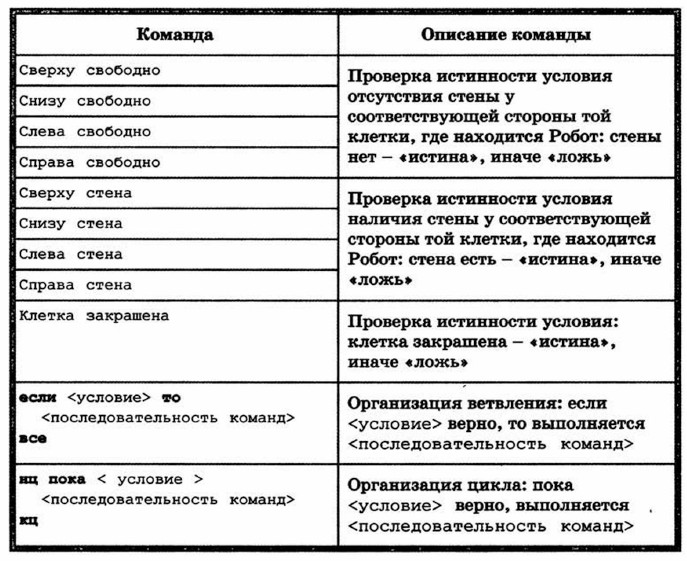
Система команд исполнителя Робот:
В одном условии можно использовать несколько команд, применяя логические операций И, ИЛИ, НЕ.
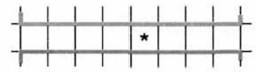
Известно, что Робот находится где-то в горизонтальном коридоре. Ни одна из клеток коридора не закрашена.
Составим алгоритм, под управлением которого Робот закрасит все клетки этого коридора и вернётся в исходное положение.
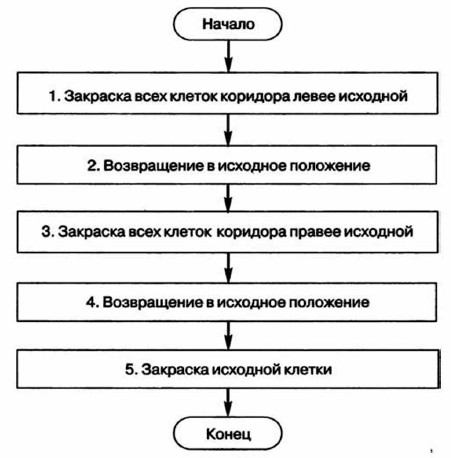
Представим план действий Робота следующими укрупнёнными шагами (модулями):
Детализируем каждый из пяти модулей.
1. Чтобы закрасить все клетки коридора, находящиеся левее Робота, прикажем Роботу шагнуть влево и выполнить цикл-ПОКА:
Под управлением этого алгоритма Робот закрасит все клетки коридора, находящиеся левее от него, и окажется на клетке рядом с левой границей коридора.
2. Командой вправо вернём Робота в коридор. Наша задача — вернуть Робота в исходную точку. Эта точка имеет единственный отличительный признак — она не закрашена. Поэтому пока занимаемая Роботом клетка оказывается закрашенной, будем перемещать его вправо.
Под управлением этого алгоритма Робот окажется в исходной клетке.
4. Так как, выполнив предыдущий алгоритм, Робот оказался правее коридора, командой влево вернём его в коридор. Возвращение в исходную точку обеспечивается алгоритмом:
5. По команде закрасить Робот закрашивает исходную клетку.
Полностью программа управления Роботом выглядит так:
Вспомогательные алгоритмы
При построении новых алгоритмов нередко возникают ситуации, когда в разных местах алгоритма необходимо выполдение одной и той же последовательности шагов обработки данных. Для такой последовательности шагов создают отдельный алгоритм, называемый вспомогательным. В качестве вспомогательных могут использоваться алгоритмы, ранее разработанные для решения других задач.
Вспомогательный алгоритм — алгоритм, целиком используемый в составе другого алгоритма.
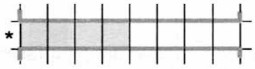
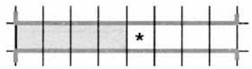
Пример 1. В среде КуМир составим алгоритм для исполнителя Робот, под управлением которого он нарисует узор:
Начальное положение Робота отмечено звёздочкой. В алгоритме использован вспомогательный алгоритм фигура.
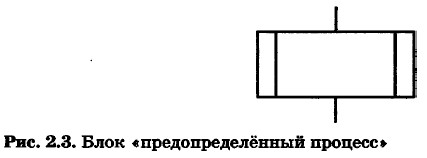
При представлении алгоритмов с помощью блок-схем для обозначения команды вызова вспомогательного алгоритма используется блок «предопределённый процесс» (рис. 2.3), внутри которого записывается название (имя) вспомогательного алгоритма, после которого в скобках перечисляются параметры — входные данные и результаты.
Вспомогательный алгоритм делает структуру алгоритма более понятной.
Пример 2.
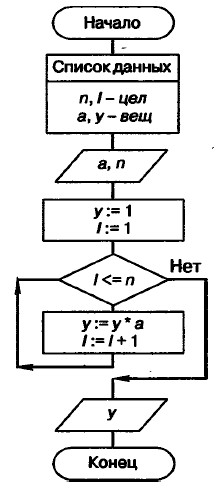
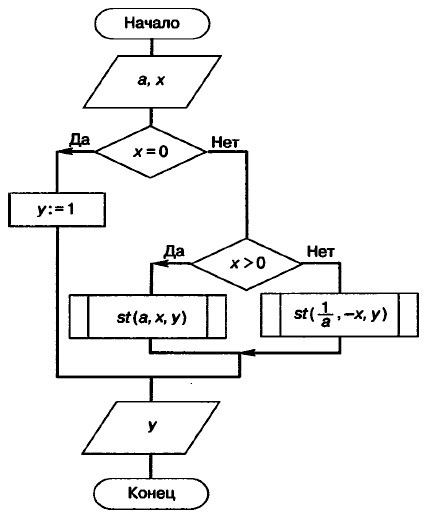
В приведённой записи дважды фигурирует вычисление степени с натуральным показателем. Поэтому в алгоритм вычисления степени с целым показателем можно включить вызов вспомогательного алгоритма вычисления степени с натуральным показателем. Соответствующая блок-схема:
Алгоритм, представленный на блок-схеме, является основным по отношению к вызываемому в нём вспомогательному алгоритму.
Параметрами используемого вспомогательного алгоритма являются величины а, n, у. Это формальные параметры, они используются при описании алгоритма. При конкретном обращении к вспомогательному алгоритму формальные параметры заменяются фактическими параметрами, т. е. именно теми величинами, для которых будет исполнен вспомогательный алгоритм. Типы, количество и порядок следования формальных и фактических параметров должны совпадать.
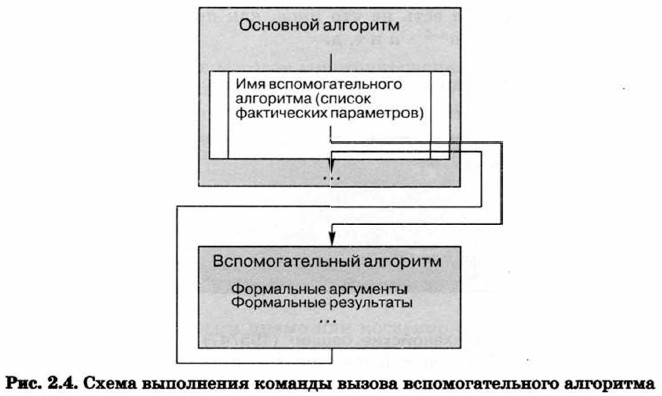
Команда вызова вспомогательного алгоритма исполняется следующим образом (рис. 2.4):
Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.
Рассмотрим несколько примеров рекурсивных алгоритмов.
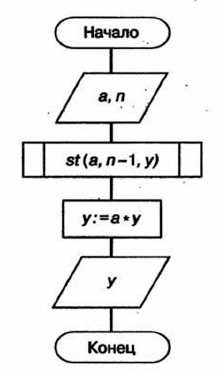
Пример 3. Алгоритм вычисления степени с натуральным показателем n для любого вещественного числа а можно представить в виде рекурсивного:
n-я степень числа а есть не что иное, как произведение а n-1 • а; в свою очередь, а n-1 = а n-2 • а и т. д.
Пример 4. Рекурсивный алгоритм положен в основу эффективно го решения головоломки «Ханойская башня».
Пример 5. Рассмотрим алгоритм построения геометрической фигуры, которая называется снежинкой Коха. Шаг процедуры построения состоит в замене средней трети каждого из имеющихся отрезков двумя новыми такой же длины, как показано на рисунке:
С каждым шагом фигура становится всё причудливее. Граница снежинки Коха — положение кривой после выполнения бесконечного числа шагов.
Попробуйте подсчитать, сколько рёбер в границе снежинки Коха после четвёртого шага; после пятого шага.
САМОЕ ГЛАВНОЕ
Один из основных методов конструирования алгоритмов — метод последовательного построения алгоритма. Его суть состоит в том, что: исходная задача разбивается на несколько частей, каждая из которых проще всей задачи, и решение каждой части формулируется в отдельной команде; если получаются команды, выходящие за пределы возможностей исполнителя, то они представляются в виде совокупности ещё более простых предписаний. Процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.Вспомогательный алгоритм — алгоритм, целиком используемый в составе другого алгоритма.Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Дополняет ли презентация информацию, содержащуюся в тексте параграфа?
В чем заключается метод последовательного уточнения при построении алгоритма
2.1:
При копировании в L5
=(L1+$K2+L$3+$K$4)/4
2.2:
При копировании в M10
=(M6+$K7+M$3+$K$4)/4
3.1:
При копировании в B19
=СРЗНАЧ(B$1:B18)
3.2:
При копировании в C22
=СРЗНАЧ(C$1:C21)
1) крик
Первоначально люди использовали лишь средства ближней связи — речь, слух, зрение. О надвигающейся опасности можно было предупредить криком, правда, услышать его могли на расстоянии всего нескольких сот метров.
2) барабан
Звук барабана, особенно популярный среди африканских племен, был способен донести сигнал тревоги уже несколько километров.
3) интернет
В 1969 году в США начала функционировать первая в компьютерная сеть. Она положила начало формированию всемирной компьютерной сети Интернет (Internet), огни миллионов компьютеров, включённых в Интернет, образуют единую информационную среду, открывающую любому человеку доступ ко всему информационному богатству человечества.
4) передатчик
Рассмотрим несколько ситуаций, связанных с передачей информации.
При переходе дороги на регулируемом перекрёстке вы (приёмник информации) воспринимаете зелёный сигнал светофора (источника информации) как разрешение перейти дорогу.
5) радиосвязь
В 1895 году русский изобретатель А. С. Попов открыв радиосвязь, не требующую проводов и кабелей. Вначале радиосвязь мало чем отличалась от телеграфа.
6) морзе
До середины 20-х годов XX века использовался специальный помехоустойчивый код Морзе. Со временем были изобретены различные способы помехозащитной записи звука и появилась звуковая радиосвязь, в человеческий быт вошли радиоприёмники. Сегодня существует очень много мощных радиостанций. Чтобы не испытывать взаимных помех, они работают на разных радиоволнах — длинных, средних, коротких, ультракоротких и дециметровых. Но до сих пор в экстремальных ситуациях, когда существуют сильные природные помехи, используют радиотелеграфный способ передачи информации.
15.Конструирование алгоритмов
Существуют различные методы конструирования (разработки, построения) алгоритмов. Мы познакомимся с одним из них — методом последовательного построения (уточнения) алгоритма. Иначе он называется методом разработки «сверху вниз», нисходящим методом или методом пошаговой детализации.
Процесс последовательного построения алгоритма выглядит следующим образом.
На первом шаге мы считаем, что перед нами совершенный исполнитель, который «всё знает и всё умеет». Поэтому достаточно определить исходные данные и результаты алгоритма, а сам алгоритм представить в виде единого предписания — постановки задачи (рис. 2.2).
Если исполнитель не обучен исполнять заданное предписание, то необходимо представить это предписание в виде совокупности более простых предписании (команд). Для этого:
Процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.
Объединяя полученные предписания в единую совокупность выполняемых в определённой последовательности команд, получаем требуемый алгоритм решения исходной задачи.
Разработка алгоритма методом последовательного уточнения для исполнителя Робот
Вы уже знакомы с исполнителем Робот. Он действует на клетчатом поле, между клетками которого могут быть стены.
Система команд исполнителя Робот:
В одном условии можно использовать несколько команд, применяя логические операций И, ИЛИ, НЕ.
Известно, что Робот находится где-то в горизонтальном коридоре. Ни одна из клеток коридора не закрашена.
Составим алгоритм, под управлением которого Робот закрасит все клетки этого коридора и вернётся в исходное положение.
Представим план действий Робота следующими укрупнёнными шагами (модулями):
Детализируем каждый из пяти модулей.
1. Чтобы закрасить все клетки коридора, находящиеся левее Робота, прикажем Роботу шагнуть влево и выполнить цикл-ПОКА:
влево
нц пока сверху стена и снизу стена
закрасить; влево
кц
Под управлением этого алгоритма Робот закрасит все клетки коридора, находящиеся левее от него, и окажется на клетке рядом с левой границей коридора.
2. Командой вправо вернём Робота в коридор. Наша задача — вернуть Робота в исходную точку. Эта точка имеет единственный отличительный признак — она не закрашена. Поэтому пока занимаемая Роботом клетка оказывается закрашенной, будем перемещать его вправо.
вправо.
вправо
нц пока клетка закрашена
вправо
кц
Под управлением этого алгоритма Робот окажется в исходной клетке.
4. Так как, выполнив предыдущий алгоритм, Робот оказался правее коридора, командой влево вернём его в коридор. Возвращение в исходную точку обеспечивается алгоритмом:
влево
нц пока клетка закрашена
влево
кц
5. По команде закрасить Робот закрашивает исходную клетку.
Полностью программа управления Роботом выглядит так:
алг
нач
влево
нц пока сверху стена и снизу стена
закрасить; влево
кц
вправо
нц пока клетка закрашена
вправо
кц
вправо
нц пока сверху стена и снизу стена
закрасить; вправо
кц
влево
нц пока клетка закрашена
влево
кц
закрасить
кон
Вспомогательные алгоритмы
При построении новых алгоритмов нередко возникают ситуации, когда в разных местах алгоритма необходимо выполдение одной и той же последовательности шагов обработки данных. Для такой последовательности шагов создают отдельный алгоритм, называемый вспомогательным. В качестве вспомогательных могут использоваться алгоритмы, ранее разработанные для решения других задач.
 Вспомогательный алгоритм — алгоритм, целиком используемый в составе другого алгоритма. |
Пример 1. В среде КуМир составим алгоритм для исполнителя Робот, под управлением которого он нарисует узор:
Начальное положение Робота отмечено звёздочкой. В алгоритме использован вспомогательный алгоритм фигура.
использовать Робот
алг узор
нач
фигура
вправо; вниз
фигура
вправо; вниз
фигура
кон
алг фигура
нач
закрасить; вниз
закрасить; вправо; закрасить; вправо; закрасить
вверх; закрасить
кон
При представлении алгоритмов с помощью блок-схем для обозначения команды вызова вспомогательного алгоритма используется блок «предопределённый процесс» (рис. 2.3), внутри которого записывается название (имя) вспомогательного алгоритма, после которого в скобках перечисляются параметры — входные данные и результаты.
Вспомогательный алгоритм делает структуру алгоритма более понятной.
Пример 2.
Вспомогательные алгоритмы (продолжение)
В приведённой записи дважды фигурирует вычисление степени с натуральным показателем. Поэтому в алгоритм вычисления степени с целым показателем можно включить вызов вспомогательного алгоритма вычисления степени с натуральным показателем. Соответствующая блок-схема:
Алгоритм, представленный на блок-схеме, является основным по отношению к вызываемому в нём вспомогательному алгоритму.
| Параметрами используемого вспомогательного алгоритма являются величины а, n, у. Это формальные параметры, они используются при описании алгоритма. При конкретном обращении к вспомогательному алгоритму формальные параметры заменяются фактическими параметрами, т. е. именно теми величинами, для которых будет исполнен вспомогательный алгоритм. Типы, количество и порядок следования формальных и фактических параметров должны совпадать. |
Команда вызова вспомогательного алгоритма исполняется следующим образом (рис. 2.4):
1) формальные входные данные вспомогательного алгоритма заменяются значениями фактических входных данных, указанных в команде вызова вспомогательного алгоритма;
2) для заданных входных данных исполняются команды вспомогательного алгоритма;
3) полученные результаты присваиваются переменным с именами фактических результатов;
4) осуществляется переход к следующей команде основного алгоритма.
| Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным. |
Вспомогательные алгоритмы (окончание)
Рассмотрим несколько примеров рекурсивных алгоритмов.
Пример 3. Алгоритм вычисления степени с натуральным показателем n для любого вещественного числа а можно представить в виде рекурсивного:
n-я степень числа а есть не что иное, как произведение а n-1 • а; в свою очередь, а n-1 = а n-2 • а и т. д.
Пример 4. Рекурсивный алгоритм положен в основу эффективно го решения головоломки «Ханойская башня».
Интерактивная игра «Ханойские башни» (195747) поможет вам вспомнить условие и алгоритм решения головоломки (http://sc.edu.ru/).
Пример 5. Рассмотрим алгоритм построения геометрической фигуры, которая называется снежинкой Коха. Шаг процедуры построения состоит в замене средней трети каждого из имеющихся отрезков двумя новыми такой же длины, как показано на рисунке:
С каждым шагом фигура становится всё причудливее. Граница снежинки Коха — положение кривой после выполнения бесконечного числа шагов.
Попробуйте подсчитать, сколько рёбер в границе снежинки Коха после четвёртого шага; после пятого шага.