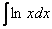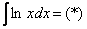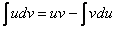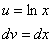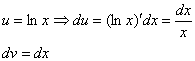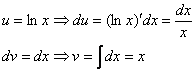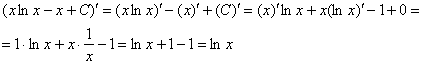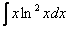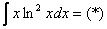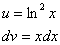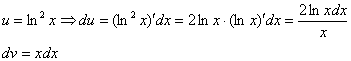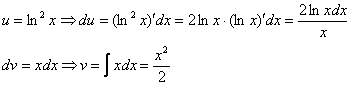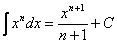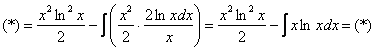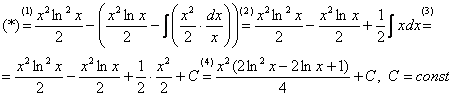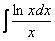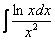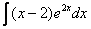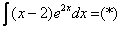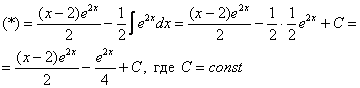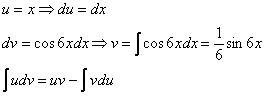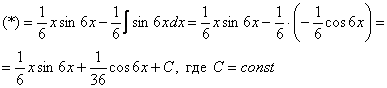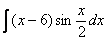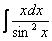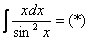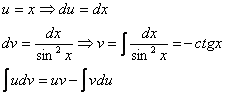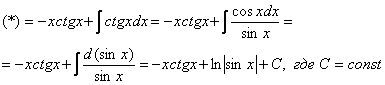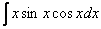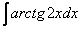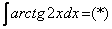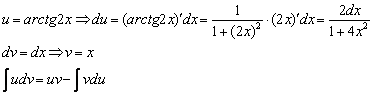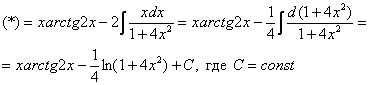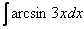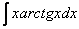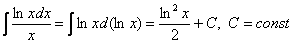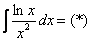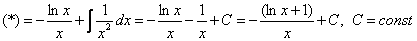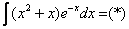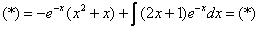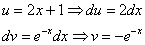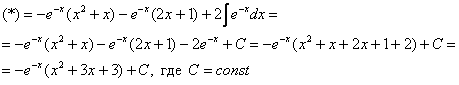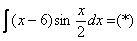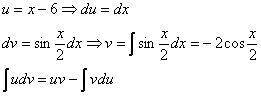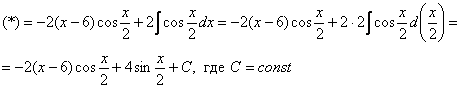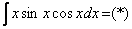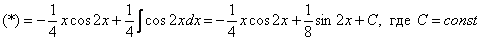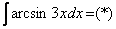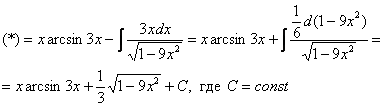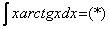в чем заключается метод интегрирования по частям
Методы интегрирования
Вычислить первообразные функции мы можем не всегда, но задача на дифференцирование может быть решена для любой функции. Именно поэтому единого метода интегрирования, который можно использовать для любых типов вычислений, не существует.
В рамках данного материала мы разберем примеры решения задач, связанных с нахождением неопределенного интеграла, и посмотрим, для каких типов подынтегральных функций подойдет каждый метод.
Метод непосредственного интегрирования
Основной метод вычисления первообразной функции – это непосредственное интегрирование. Это действие основано на свойствах неопределенного интеграла, и для вычислений нам понадобится таблица первообразных. Прочие методы могут лишь помочь привести исходный интеграл к табличному виду.
Решение
Мы знаем, что интеграл суммы функций будет равен сумме этих интегралов, значит:
∫ f ( x ) d x = ∫ 3 2 · 5 x + 4 3 = 2 x + 3 2 · 5 x + 4 1 3 d x = ∫ 3 2 · 5 x + 4 1 3 d x
Выводим за знак интеграла числовой коэффициент:
∫ f ( x ) d x = ∫ 2 x d x + ∫ 3 2 ( 5 x + 4 ) 1 3 d x = = ∫ 2 x d x + 2 3 · ∫ ( 5 x + 4 ) 1 3 d x
Чтобы найти первый интеграл, нам нужно будет обратиться к таблице первообразных. Берем из нее значение ∫ 2 x d x = 2 x ln 2 + C 1
Следовательно, ∫ f ( x ) d x = ∫ 2 x d x + 3 2 · ∫ 5 x + 4 1 3 d x = = 2 x ln 2 + C 1 + 3 2 · 3 20 · ( 5 x + 4 ) 4 3 + C 2 = = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C
У нас получилось следующее:
∫ f ( x ) d x = ∫ 2 x d x + 3 2 · ∫ 5 x + 4 1 3 d x = = 2 x ln 2 + C 1 + 3 2 · 3 20 · ( 5 x + 4 ) 4 3 + C 2 = = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C
причем C = C 1 + 3 2 C 2
Ответ: ∫ f ( x ) d x = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C
Непосредственному интегрированию с применением таблиц первообразных мы посвятили отдельную статью. Рекомендуем вам ознакомиться с ней.
Метод подстановки
Такой метод интегрирования заключается в выражении подынтегральной функции через новую переменную, введенную специально для этой цели. В итоге мы должны получить табличный вид интеграла или просто менее сложный интеграл.
Этот метод очень полезен, когда нужно интегрировать функции с радикалами или тригонометрические функции.
Решение
Далее подставляем полученные выражения в исходный интеграл и получаем:
Теперь нам нужно вернуться к переменной x и получить ответ:
Как мы говорили выше, метод подстановки удобно использовать, когда требуется интегрировать тригонометрическую функцию. Например, с помощью универсальной подстановки можно привести выражение к дробно рациональному виду.
Теперь берем получившиеся выражения и добавляем их в интеграл, заданный в условии:
∫ f ( k · x + b ) d x = ∫ f ( z ) · d z k = 1 k · ∫ f ( z ) d z = = 1 k · F z + C 1 = F ( z ) k + C 1 k
F ( z ) k + C 1 k = 1 k · F k x + b + C
Метод подведения под знак дифференциала
∫ f ( g ( x ) ) d ( g ( x ) ) = g ( x ) = z = ∫ f ( z ) d ( z ) = = F ( z ) + C = z = g ( x ) = F ( g ( x ) ) + C
Чтобы быстрее решать задачи с использованием этого метода, держите под рукой таблицу производных в виде дифференциалов и таблицу первообразных, чтобы найти выражение, к которому надо будет приводится подынтегральное выражение.
Разберем задачу, в которой нужно вычислить множество первообразных функции котангенса.
Решение
Преобразуем исходное выражение под интегралом с помощью основных тригонометрических формул.
c t g x d x = cos s d x sin x
Все решение в кратком виде можно записать так:
∫ с t g x d x = ∫ cos x d x sin x = ∫ d sin x sin x = s i n x = t = = ∫ d t t = ln t + C = t = sin x = ln sin x + C
Ответ: ∫ с t g x d x = ln sin x + C
Метод подведения под знак дифференциала очень часто используется на практике, поэтому советуем вам прочесть отдельную статью, посвященную ему.
Метод интегрирования по частям
Разберем задачу, в которой нужно вычислить множество первообразных арктангенса.
Решение
d ( u ( x ) ) = u ‘ ( x ) d x = a r c t g ( 2 x ) ‘ d x = 2 d x 1 + 4 x 2 v ( x ) = ∫ d ( v ( x ) ) = ∫ d x = x
Далее используем формулу интегрирования по частям и получаем:
Получившийся интеграл вычисляем, используя метод подведения под знак дифференциала.
Если нам требуется найти множество первообразных дробно рациональной функции, то нужно сначала представить подынтегральную функцию в виде суммы простейших дробей, а потом интегрировать получившиеся дроби. Подробнее см. статью об интегрировании простейших дробей.
Подведем итоги. Для решения задач очень важно знать метод непосредственного интегрирования. Другие методы (подведение под знак дифференциала, подстановка, интегрирование по частям) также позволяют упростить интеграл и привести его к табличному виду.
Интегрирование по частям. Примеры решений
И снова, здравствуйте. Сегодня на уроке мы научимся интегрировать по частям. Метод интегрирования по частям – это один из краеугольных камней интегрального исчисления. На зачете, экзамене студенту почти всегда предлагают решить интегралы следующих типов: простейший интеграл (см. статью Неопределенный интеграл. Примеры решений) либо интеграл на замену переменной (см. статью Метод замены переменной в неопределенном интеграле) либо интеграл как раз на метод интегрирования по частям.
Для эффективного изучения темы необходимо хорошо ориентироваться в материалах двух вышеуказанных уроков. Если Вы чайник, и только-только начинаете погружение в удивительный мир интегралов, то читать далее не имеет особого смысла – следует начать с урока Неопределенный интеграл. Примеры решений.
Как всегда, под рукой должны быть: Таблица интегралов и Таблица производных. Если у Вас до сих пор их нет, то, пожалуйста, посетите кладовку моего сайта: Математические формулы и таблицы. Не устану повторять – лучше всё распечатать. Весь материал я постараюсь изложить последовательно, просто и доступно, в интегрировании по частям нет особых трудностей.
Какую задачу решает метод интегрирования по частям? Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение функций, а в ряде случаев – и частное. Как мы помним, нет удобной формулы:
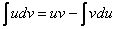
И сразу список в студию. По частям берутся интегралы следующих видов:
1) 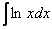
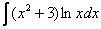
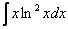
2) 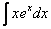
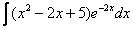
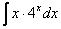
3) 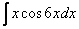
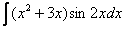
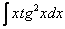
4) 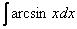
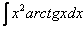
Также по частям берутся некоторые дроби, соответствующие примеры мы тоже подробно рассмотрим.
Интегралы от логарифмов
Найти неопределенный интеграл.
Классика. Время от времени данный интеграл можно встретить в таблицах, но пользоваться готовым ответом нежелательно, так как у преподавателя весенний авитаминоз и он сильно заругается. Потому что рассматриваемый интеграл отнюдь не табличный – он берётся по частям. Решаем:
Прерываем решение на промежуточные объяснения.
Используем формулу интегрирования по частям:
Формула применяется слева направо
Смотрим на левую часть: 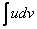
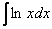
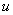
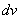
В интегралах рассматриваемого типа за 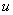
Технически оформление решения реализуется следующим образом, в столбик записываем:
То есть, за 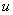
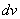
Следующий этап: находим дифференциал 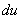
Дифференциал – это почти то же самое, что и производная, как его находить, мы уже разбирали на предыдущих уроках.
Теперь находим функцию 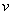
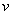
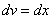
Теперь открываем наше решение и конструируем правую часть формулы: 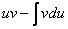
Вот кстати, и образец чистового решения с небольшими пометками:

Единственный момент, в произведении 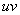
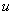
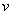
Как видите, применение формулы интегрирования по частям, по сути дела, свело наше решение к двум простым интегралам.
Обратите внимание, что в ряде случаев сразу после применения формулы, под оставшимся интегралом обязательно проводится упрощение – в рассматриваемом примере мы сократили подынтегральное выражение на «икс».
Выполним проверку. Для этого нужно взять производную от ответа:
Получена исходная подынтегральная функция, значит, интеграл решён правильно.
В ходе проверки мы использовали правило дифференцирования произведения: 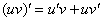
Формула интегрирования по частям 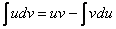
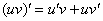
Найти неопределенный интеграл.
Подынтегральная функция представляет собой произведение логарифма на многочлен.
Решаем.
Я еще один раз подробно распишу порядок применения правила, в дальнейшем примеры будут оформляться более кратко, и, если у Вас возникнут трудности в самостоятельном решении, нужно вернуться обратно к первым двум примерам урока.
Как уже говорилось, за 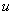

Записываем в столбик:
Сначала находим дифференциал 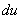
Здесь использовано правило дифференцирования сложной функции 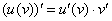
Теперь находим функцию 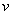
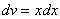
Для интегрирования мы применили простейшую табличную формулу
Теперь всё готово для применения формулы 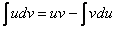
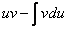
Под интегралом у нас снова многочлен на логарифм! Поэтому решение опять прерывается и правило интегрирования по частям применяется второй раз. Не забываем, что за 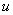
Хорошо бы, если к данному моменту простейшие интегралы и производные Вы умели находить устно.
(1) Не путаемся в знаках! Очень часто здесь теряют минус, также обратите внимание, что минус относится ко всей скобке 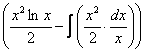
(2) Раскрываем скобки. Последний интеграл упрощаем.
(3) Берем последний интеграл.
(4) «Причесываем» ответ.
Необходимость дважды (а то и трижды) применять правило интегрирования по частям возникает не так уж и редко.
А сейчас пара примеров для самостоятельного решения:
Найти неопределенный интеграл.
Этот пример решается методом замены переменной (или подведением под знак дифференциала)! А почему бы и нет – можете попробовать взять его по частям, получится забавная вещь.
Найти неопределенный интеграл.
А вот этот интеграл интегрируется по частям (обещанная дробь).
Это примеры для самостоятельного решения, решения и ответы в конце урока.
Вроде бы в примерах 3, 4 подынтегральные функции похожи, а вот методы решения – разные! В этом-то и состоит основная трудность освоения интегралов – если неправильно подобрать метод решения интеграла, то возиться с ним можно часами, как с самой настоящей головоломкой. Поэтому чем больше вы прорешаете различных интегралов – тем лучше, тем легче пройдут зачет и экзамен. Кроме того, на втором курсе будут дифференциальные уравнения, а без опыта решения интегралов и производных делать там нечего.
По логарифмам, пожалуй, более чем достаточно. На закуску могу еще вспомнить, что студенты-технари логарифмами называют женскую грудь =). Кстати, полезно знать назубок графики основных элементарных функций: синуса, косинуса, арктангенса, экспоненты, многочленов третьей, четвертой степени и т.д. Нет, конечно, презерватив на глобус
я натягивать не буду, но теперь вы многое запомните из раздела Графики и функции =).
Интегралы от экспоненты, умноженной на многочлен
Общее правило: за 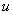
Найти неопределенный интеграл.
Используя знакомый алгоритм, интегрируем по частям:

Если возникли трудности с интегралом 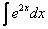
Единственное, что еще можно сделать, это «причесать» ответ:
Но если Ваша техника вычислений не очень хороша, то самый выгодный вариант оставить ответом 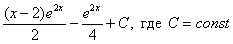
То есть, пример считается решенным, когда взят последний интеграл. Ошибкой не будет, другое дело, что преподаватель может попросить упростить ответ.
Найти неопределенный интеграл.
Это пример для самостоятельного решения. Данный интеграл дважды интегрируется по частям. Особое внимание следует обратить на знаки – здесь легко в них запутаться, также помним, что 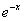
Больше про экспоненту рассказывать особо нечего. Могу только добавить, что экспонента и натуральный логарифм взаимно-обратные функции, это я к теме занимательных графиков высшей математики =) Стоп-стоп, не волнуемся, лектор трезв.
Интегралы от тригонометрических функций, умноженных на многочлен
Общее правило: за 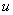
Найти неопределенный интеграл.
Интегрируем по частям:
Хммм, …и комментировать нечего.
Найти неопределенный интеграл
Это пример для самостоятельного решения
Найти неопределенный интеграл
Еще один пример с дробью. Как и в двух предыдущих примерах за 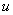
Интегрируем по частям:
Если возникли трудности или недопонимание с нахождением интеграла 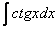
Найти неопределенный интеграл
Это пример для самостоятельного решения.
Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.
Вот, пожалуй, и всё в данном параграфе. Почему-то вспомнилась строчка из гимна физмата «А синуса график волна за волной по оси абсцисс пробегает»….
Интегралы от обратных тригонометрических функций.
Интегралы от обратных тригонометрических функций, умноженных на многочлен
Общее правило: за 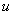
Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками»
Найти неопределенный интеграл.
Интегрируем по частям:
Интеграл 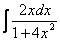
И здесь читатель задал вопрос: а куда же делся модуль под логарифмом? Ответ прост: если «начинка» логарифма неотрицательна (при любом возможном «икс»), то модуль можно не ставить. В данном примере 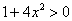
Найти неопределенный интеграл.
Это пример для самостоятельного решения.
Как видите, помимо «чистого» интегрирования по частям нередко требуется применять и другие методы, приёмы решения.
И заключительный пример сегодняшнего урока под счастливым номером тринадцать: «арк», умноженный на многочлен. Он сложнее, и предназначен для маньяков желающих лучше разобраться в методе интегрирования по частям. Пример, пожалуй, будет тоже для самостоятельного решения, поскольку меня немного утомил тот логарифм в квадрате.
Найти неопределенный интеграл.
Что касаемо интегрирования по частям, почти всё разобрали. Рассмотренный метод часто применяется в комбинации с другими приёмами решения интегралов. Читатели с хорошими навыками могут ознакомиться с такими примерами на уроке Сложные интегралы.
Пример 3: Решение:
Пример 4: Решение:
Интегрируем по частям:
Пример 6: Решение:
Дважды интегрируем по частям:
Пример 8: Решение:
Интегрируем по частям:
Пример 10: Решение:
Интегрируем по частям: 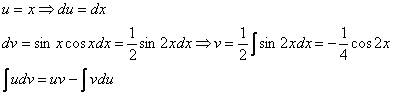
Примечание: Здесь мы использовали известную тригонометрическую формулу двойного угла 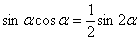
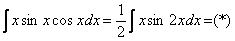
Похожим способом также решаются интегралы вроде 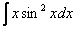
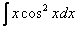
Пример 12: Решение:
Интегрируем по частям: 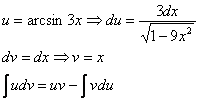
Пример 13: Решение:
Интегрируем по частям:
Примечание: Если возникли трудности с интегралом 
Вы выполнили проверку? Может я и ошибся где… 😉
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5