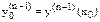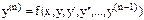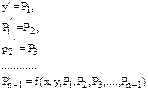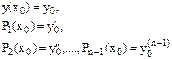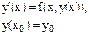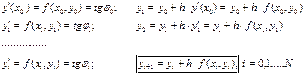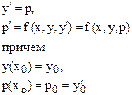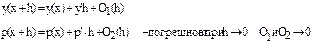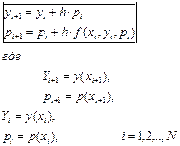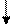в чем заключается метод эйлера

Метод Эйлера: для чего он нужен, порядок действий и упражнения

Содержание:

В Метод Эйлера Это самая базовая и простая из процедур, используемых для нахождения приближенных численных решений обыкновенного дифференциального уравнения первого порядка, при условии, что известно его начальное условие.

Если наибольшая производная, которая появляется в уравнении, имеет степень один, то это обыкновенное дифференциальное уравнение первой степени.

Самый общий способ написать уравнение первой степени:

Что такое метод Эйлера?

Сначала интервал дискретизируется на n + 1 балл:

Которые получаются так:
Икс_я= х₀+ я

С начальным условием также можно узнать производную в начале:

Эта производная представляет собой наклон касательной к кривой функции y (x) точно в точке:

Затем делается приблизительный прогноз значения функции y (x) в следующей точке:

Затем была получена следующая приближенная точка решения, которая будет соответствовать:

Процедура повторяется для получения последовательных баллов.

Решенные упражнения

Упражнение 1

я) Пусть дифференциальное уравнение имеет вид:

При начальном условии x = a = 0; Y_к= 1

Используя метод Эйлера, получить приближенное решение Y в координате X = b = 0,5, разбивая интервал [a, b] на n = 5 частей.

Решение

Численные результаты резюмируются следующим образом:

Из чего делается вывод, что решение Y для значения 0,5 составляет 1,4851.

Примечание: для проведения расчетов, Smath studio, бесплатная программа для бесплатного использования.

Упражнение 2.

II) Продолжая работу с дифференциальным уравнением из упражнения I), найдите точное решение и сравните его с результатом, полученным методом Эйлера. Найдите ошибку или разницу между точным и приблизительным результатом.

Решение

Точное решение найти не очень сложно. Производная функции sin (x) известна как функция cos (x). Следовательно, решение y (x) будет:

Для выполнения начального условия и (0) = 1 константа C должна быть равна 1. Затем точный результат сравнивается с приблизительным:

Сделан вывод, что в расчетном интервале аппроксимация имеет три значащих цифры точности.

Упражнение 3.

III) Рассмотрим дифференциальное уравнение и его начальные условия, указанные ниже:

При начальном условии x₀ = 0; Y₀ = 1

Используйте метод Эйлера, чтобы найти приблизительные значения решения у (х) в интервале х = [0, 1,5]. Используйте шаг h = 0,1.

Решение

Метод Эйлера очень подходит для использования с электронной таблицей. В этом случае мы будем использовать электронную таблицу геогебра бесплатная и бесплатная программа.

Точно так же y2 будет в ячейке B4, и его формула показана на следующем рисунке:

На рисунке также показан график точного решения и точки A, B,…, P приближенного решения по методу Эйлера.

Ньютоновская динамика и метод Эйлера

Второй закон Ньютона обычно выражается в виде дифференциального уравнения второй степени:

куда Икс представляет положение объекта в момент т. Указанный объект имеет массу м и подвергается силе F. Функция F связана с силой и массой следующим образом:

Для применения метода Эйлера требуются начальные значения времени. т, скорость v и положение Икс.

В следующей таблице объясняется, как, начиная с начальных значений t1, v1, x1, можно получить приближение скорости v2 и положения x2 в момент t2 = t1 + Δt, где Δt представляет небольшое увеличение и соответствует шагу в методе Эйлер.

Упражнение 4.

Второй закон Ньютона для этой проблемы будет выглядеть так:

В этом примере для простоты мы возьмем M = 1 и K = 1. Найдите приблизительные решения для положения Икс и скорость v методом Эйлера на временном интервале [0, π / 2], разбивая интервал на 12 частей.

Возьмите 0 в качестве начального момента, начальную скорость 0 и начальное положение 1.

Решение

Численные результаты представлены в следующей таблице:

Также отображаются графики положения и скорости между временами от 0 до 1,44.

Предлагаемые упражнения для дома

Упражнение 1

Используйте электронную таблицу, чтобы найти приближенное решение с помощью метода Эйлера для дифференциального уравнения:

Начните с шага 0,1. Постройте результат.

Упражнение 2.

Используя электронную таблицу, найдите численные решения следующего квадратного уравнения, где y является функцией независимой переменной t.

Найдите решение на интервале [0,5; 1.0] с шагом 0,05.

Источник

Метод Эйлера

Содержание

Описание метода

Пусть дана задача Коши для уравнения первого порядка

где функция определена на некоторой области . Решение разыскивается на интервале . На этом интервале введем узлы

Приближенное решение в узлах , которое обозначим через определяется по формуле

Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.

Оценка погрешности

Метод Эйлера является методом первого порядка. Если функция непрерывна в и непрерывно дифференцируема по переменной в , то имеет место следующая оценка погрешности

где — средний шаг, то есть существует 0″ border=»0″ /> такая, что .

Заметим, что условия гладкости на правую часть, гарантирующие единственность решения задачи Коши, необходимы для обоснования сходимости метода Эйлера.

Значение метода Эйлера

Метод Эйлера являлся исторически первым методом численного решения задачи Коши. О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.

Модифицированный метод Эйлера с пересчетом

Вычисления по методу Эйлера с пересчетом делаются в два этапа.

.

.

Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо дважды вычислять правую часть функции. Заметим, что метод Эйлера с пересчетом представляет собой разновидность методов Рунге-Кутты (предиктор-корректор).

См. также

Литература

Примечания

Полезное

Смотреть что такое «Метод Эйлера» в других словарях:

метод Эйлера — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN Eulers method … Справочник технического переводчика

Метод Рунге — Кутта — Методы Рунге Кутта (Методы Рунге Кутты) важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года… … Википедия

ЭЙЛЕРА МЕТОД — простейший конечно разностный метод численного решения обыкновенных дифференциальных уравнений. Пусть дано дифференциальное уравнение с начальным условием y(x0) = y0. Выбирается достаточно малый шаг hпо оси х, строятся точки x;=x0+ih, i=0, 1, 2 … Математическая энциклопедия

Метод Рунге — Методы Рунге Кутты (распространено неправильное название Методы Рунге Кутта или даже Методы Рунге Кутта) важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные … Википедия

Метод Рунге — Кутты — Методы Рунге Кутта важное семейство численных алгоритмов решения (систем) обыкновенных дифференциальных уравнений. Данные итеративные методы явного и неявного приближенного вычисления были разработаны около 1900 года немецкими математиками К.… … Википедия

Метод Рунге-Кутта — Методы Рунге Кутта важное семейство численных алгоритмов решения (систем) обыкновенных дифференциальных уравнений. Данные итеративные методы явного и неявного приближенного вычисления были разработаны около 1900 года немецкими математиками К.… … Википедия

Метод Рунге-Кутты — Методы Рунге Кутта важное семейство численных алгоритмов решения (систем) обыкновенных дифференциальных уравнений. Данные итеративные методы явного и неявного приближенного вычисления были разработаны около 1900 года немецкими математиками К.… … Википедия

Метод Рунге — Куттa — Методы Рунге Кутта важное семейство численных алгоритмов решения (систем) обыкновенных дифференциальных уравнений. Данные итеративные методы явного и неявного приближенного вычисления были разработаны около 1900 года немецкими математиками К.… … Википедия

ЭЙЛЕРА МЕТОД — построения таблиц смертности, основан на использовании данных о возрастном составе умерших и коэфф. естеств. прироста населения (r) за предшествующий период. Э. м. позволяет адекватно оценить уровень смертности т. н. закрытого населения (без… … Демографический энциклопедический словарь

Источник

Решение обыкновенных дифференциальных уравнений. Метод Эйлера

КОБЕЦ Е.В.

ЛЕКЦИОННЫЙ МАТЕРИАЛ

ПО ДИСЦИПЛИНЕ «КОМПЬЮТЕРНОЕ

ОБЕСПЕЧЕНИЕ»

Решение обыкновенных дифференциальных уравнений. Метод Эйлера

Обыкновенные дифференциальные уравнения встречаются достаточно часто в различных прикладных задачах. Ими описываются задачи движения систем материальных точек, электрических цепей и др.

Дифференциальным называется такое уравнение, которое связывает независимую переменную Х, ее функцию y=f(x) и производные этой функции .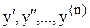

В неявном виде дифференциальное уравнение записывается так:

F(x, y, 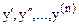)=0.

Порядок старшей производной, входящей в это уравнение, называется порядком дифференциального уравнения.

Если y=f(x) – функция одного независимого переменного Х, дифференциальное уравнение называется обыкновенным, если же y=f(x₁,x₂,…x_n) – функция n независимых переменных x₁,x₂,…x_n, то уравнение называется уравнением в частных производных.

Решение обыкновенного дифференциального уравнения сводится к поиску функции y=f(x), которая при подстановке в уравнение обращает его в тождество.

Поиск решения такого уравнения называется его интегрированием, а полученное решение – интегралом этого уравнения.

Существуют общее и частное решения дифференциального уравнения.

Общим решением уравнения 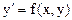является функция y=φ(x,c), удовлетворяющая уравнению при любых значениях постоянного С.

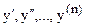
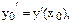
Частное решение определяется конкретным значением С. Для нахождения частного решения необходимо указать начальные условия, т.е. задать значения y, при х=х₀, т.е. y₀=y(x₀), …,

Задача отыскания решения обыкновенного дифференциального уравнения при начальных условиях называется задачей Коши для обыкновенного дифференциального уравнения.

Мы рассматриваем уравнения разрешенными относительно старшей производной.

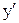
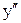
Их можно свести к системе n обыкновенных дифференциальных уравнений первого порядка заменой на неизвестную функцию Р₁(х), на Р₂(х) и т.д., т.е.

Причем, начальные условия:

Для решения мы будем рассматривать методы Эйлера и Рунге-Кутта.

Численное решение состоит в построении таблицы приближенных значений y₁,y₂,…,y_n-1 точного решения y(x) уравнения .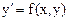

Мы не знаем вида функции, не можем сразу вычислить значение функции. Знаем только начальные условия, значения Х₀=а, y₀=y(x₀) и интервал [a,b], на котором необходимо проинтегрировать функцию.

Задача ставится так: в точках Х₀,X₁,…,Х_n нужно найти приближения y₀,y₁,…,y_n точного решения.

Первый шаг – разбиваем отрезок на конечное число узловых точек (узлы сетки). Шаг сетки h=(b-a)/n, X_i=a+ih, I=0,1. N.

Нужно восстановить значения искомой функции. Рассмотрим дифференциальное уравнение 1 порядка

Второй шаг – зная начальные условия вычисляем значение первой производной в точке Х₀.

Третий шаг – в следующем узле сетки вычисляем значение функции.

На четвертом шаге все повторяется.

Геометрическая интерпритация метода состоит в замене интегральной кривой на отрезке касательной к ней в точке x_i,y_i. На каждом шаге заново определяется касательная, и, следовательно, соответствующая приближенному решению кривая будет ломаной линией. Поэтому метод называют еще методом ломаных.

Схема вычислений: x_i=a+ih (I=0,1,…,N)

Т.е. имея известную точку, вычисляем следующую. Это схема вычислений для уравнения 1 порядка.

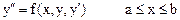
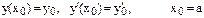
Метод Эйлера для уравнений 2 порядка надо уравнение с начальными условиями свести к системе 2 уравнений 1-го порядка:

Производные берутся в точке х.

Итерационная формула вычислений:

На практике вычисления проводятся снизу вверх: вначале вычисляется 1 производную, т.е. p_i, а затем вторую Y_i.

Для уравнения второго порядка приходится дважды применять интегрирование. Восстанавливаем значение производной, а затем значение искомой функции, т.е. решаем вначале одно уравнение, а затем второе.

Пример. На отрезке [a,b] составить таблицу значений приближенного решения дифференциального уравнения 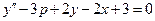, удовлетворяющего начальным условиям

Y(0)=1, Y΄(0)=2. шаг интегрирования h=0,2, точность ε=0,001. Предусмотреть печать значений точного решения y=e x +x.

Нужен массив Х – значений Х от 0 до 2

У – массив приближенных решений

Р – массив значений производной

(a-b)/h+ начальная точка = 2/0,2=10+1=11

Рассмотренный метод Эйлера относится к группе одношаговых методов, в которых для расчета точки (x_i+1, y_i+1) требуется информация о последней вычислительной точке (x_i, y_i).

Численное решение состоит в построении таблицы приближенных значений y₁, y₂, y₃, …,y_n-1 точного решения y(x) уравнения y¢=f(x,y), a£x£b при начальном условии y(x₀)=y₀, x₀=a на выбранной последовательности точек x_i=x₀+ih. Функция y зависит от аргумента х

Точность метода или ошибкой обрыва называют ошибку, которую делают при переходе от предыдущего к последующему Х, если заменяют дифференциальное уравнение конечностным выражением.

Погрешность аппроксимации разностными уравнениями равна величине отброшенного остаточного члена ряда Тейлора O(h p +1 ).

В методе Эйлера сравнение формулы вычисления с разложением в ряд Тейлора согласуется до первого порядка по h, т.е. метод имеет первый порядок точности с локальной погрешностью O(h 2 )

10.2. ЧИСЛЕННЫЙ МЕТОД ПОСТРОЕНИЯ ГРАФИКОВ

При решении задач на ЭВМ важное значение имеет наглядность и удобство быстрого восприятия изучаемых явлений. После освоения средств графического режима Турбо Паскаля можно строить графики, а также получать различные геометрические фигуры. Какие бы изображения не выводились на экран, все они строятся из точек, группы которых в свою очередь образуют отрезки и кривые. Вывод точки осуществляется процедурой PutPixel(X, Y, Color), где Х и Y-координаты экрана, где будет расположена точка. Color — ее цвет.

Для построения графика функции необходимо осуществить следующие операции:

1) Табулирование функции;

2) Нахождение максимального и минимального значений функции;

3) Формирование и вывод графика на экран.

Табулирование функции можно осуществить с помощью следующих операторов:

х := xStart;

for i : = 1 to n do begin

y[ i ] :=F(x);

if y[ i ] a then

где а — уровень ограничения.

Для определения масштаба вычерчиваемого графика необходимо найти минимальное и максимальное значения элементов массива Y. Это достигается с помощью операторов

Источник

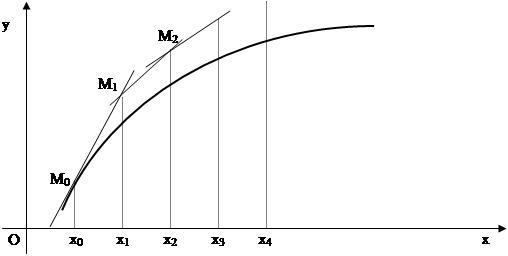
Метод Эйлера. В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения, этот метод называется также методом ломаных Эйлера

В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения, этот метод называется также методом ломаных Эйлера.

Угловой коэффициент касательной к интегральной кривой в точке M₀(x₀,y₀) равен .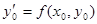

Найдем ординату y₁ касательной, соответствующей абсциссе x₁=x₀+h.

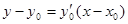
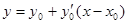
Уравнение касательной к кривой в точке M₀ имеет вид или , откуда y₁=y₀+hf(x₀,y₀).

Аналогично, угловой коэффициент касательной к интегральной кривой в точке M₁(x₁,y₁) равен 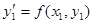. Точку M₂(x₂,y₂) получим соответственно

Продолжая вычисления по данной схеме, получим формулы Эйлера для приближенного решения задачи Коши с начальными данными (x₀,y₀) на сетке отрезка [a, b] с шагом h:

Графической иллюстрацией приближенного решения является ломаная, соединяющая последовательно точки M₀, M₁, …,M_m, которую называют ломаной Эйлера.

Погрешность метода Эйлера можно оценить неравенством

, (5)

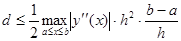
которое можно представить в виде d=Ch, где 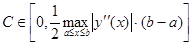. Таким образом, метод Эйлера имеет первый порядок точности.

Практическую оценку погрешности решения, найденного на сетке с шагом h/2, в точке x_iÎ[a, b] производят с помощью приближенного равенства – правила Рунге:

(6)

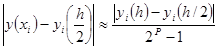
где P – порядок точности численного метода.

Таким образом, оценка полученного результата по правилу Рунге вынуждает проводить вычисления дважды: с шагом h и h/2, причем совпадение десятичных знаков в полученных двумя способами результатах дает основание считать их верными.

Программа решения дифференциального уравнения методом Эйлера

function f(x,y: real): real;

begin writeln(‘Введите значения концов отрезка [a,b]’);

writeln(‘Введите начальное значение y0=y(x0)’);readln(y);

writeln(‘Введите число значений функции на промежутке [a,b]’); read(m);

Источник