в чем заключается физический смысл волновой функции
В чем заключается физический смысл волновой функции
Важным этапом в создании квантовой механики явилось обнаружение волновых свойств микрочастиц. Идея о волновых свойствах была первоначально высказана как гипотеза французским физиком Луи де Бройлем.
В физике в течение многих лет господствовала теория, согласно которой свет есть электромагнитная волна. Однако после работ Планка (тепловое излучение), Эйнштейна (фотоэффект) и других стало очевидным, что свет обладает корпускулярными свойствами.
Чтобы объяснить некоторые физические явления, необходимо рассматривать свет как поток частиц-фотонов. Корпускулярные свойства света не отвергают, а дополняют его волновые свойства.
Итак, фотон-элементарная частица света, обладающая волновыми свойствами.
Логично считать, что и другие частицы-электроны, нейтроны- обладают волновыми свойствами.
Формула для импульса фотона
была использована для других микрочастиц массой m, движущихся со скоростью v:
К.Дэвиссон и Л.Джермер впервые наблюдали дифракцию электронов на монокристалле никеля.
Может возникнуть вопрос: что происходит с отдельными частицами, как образуются максимумы и минимумы при дифракции отдельных частиц?
Опыты по дифракции пучков электронов очень малой интенсивности, то есть как бы отдельных частиц, показали, что при этом электрон не «размазывается» по разным направлениям, а ведет себя как целая частица. Однако вероятность отклонения электрона по отдельным направлениям в результате взаимодействия с объектом дифракции различная. Наиболее вероятно попадание электронов в те места, которые по расчету соответствуют максимумам дифракции, менее вероятно их попадание в места минимумов. Таким образом, волновые свойства присущи не только коллективу электронов, но и каждому электрону в отдельности.
4.4.2. Волновая функция и ее физический смысл
Если силовое поле, действующее на частицу, является стационарным, то есть не зависящим от времени, то ψ-функцию можно представить в виде произведения двух сомножителей, один из которых зависит от времени, а другой от координат:
В дальнейшем будем рассматривать только стационарные состояния; ψ-функция является вероятностной характеристикой состояния частицы. Поясним смысл этого утверждения.
Отсюда следует физический смысл волновой функции:
Интегрируя выражение (4.4.5) по некоторому объему V, находим вероятность нахождения частицы в этом объеме:
4.4.3. Соотношение неопределенностей
Одним из важных положений квантовой механики являются соотношения неопределенностей, предложенные В.Гейзенбергом.
В классической физике нет каких-либо ограничений, запрещающих с любой степенью точности одновременно измерить как одну, так и другую величину, то есть Δx→0 и Δр x→ 0.
Таким образом, чем точнее определена координата x (Δx→0), тем не менее точно определена проекция р x (Δp x→ ± ), и наоборот. Аналогично,
Поясним их одним модельным экспериментом.
При изучении явления дифракции было обращено внимание на то, что уменьшение ширины щели при дифракции приводит к увеличению ширины центрального максимума. Аналогичное явление будет и при дифракции электронов на щели в модельном опыте. Уменьшение ширины щели означает уменьшение Δ x (рис. 4.4.1), это приводит к большему «размазыванию» пучка электронов, то есть к большей неопределенности импульса и скорости частиц.
Рис. 4.4.1.Пояснение к соотношению неопределенности.
Соотношение неопределенностей можно представить в виде
«Размытость» уровней приводит к неопределенности энергии ΔE излучаемого фотона и его частоты Δν при переходе системы с одного энергетического уровня на другой:
Это проявляется в уширении спектральных линий.
4.4.4.Уравнение Шредингера
Применительно к стационарным состояниям уравнение Шредингера может быть записано так:
где m- масса частицы; ; Е и Е n –ее полная и потенциальная энергии (потенциальная энергия определяется силовым полем, в котором находится частица, и для стационарного случая не зависит от времени)
Если частица перемещается только вдоль некоторой линии, например вдоль оси ОХ (одномерный случай), то уравнение Шредингера существенно упрощается и принимает вид
Одним из наиболее простых примеров на использование уравнения Шредингера является решение задачи о движении частицы в одномерной потенциальной яме.
4.4.5. Применение уравнения Шредингера к атому водорода. Квантовые числа
Описание состояний атомов и молекул с помощью уравнения Шредингера является достаточно сложной задачей. Наиболее просто она решается для одного электрона, находящегося в поле ядра. Такие системы соответствуют атому водорода и водородоподобным ионам (однократно ионизированный атом гелия, двукратно ионизированный атом лития и т.п.). Однако и в этом случае решение задачи является сложным, поэтому ограничимся лишь качественным изложением вопроса.
Состояние электрона в атоме характеризуется не одним, а несколькими квантовыми числами.
Это выражение является решением уравнения Шредингера и полностью совпадает с соответствующей формулой теории Бора (4.2.30)
Рис. 4.4.3. Показаны уровни возможных значений полной энергии атома водорода
и график зависимости потенциальной энергии от расстояния r между электроном и ядром.
Состояние электрона в атоме с заданными n и l обозначают следующим образом: 1s, 2s, 2p, 3s и т.д. Здесь цифра указывает значение главного квантового числа, а буква – орбитальное квантовое число: символам s, p, d, f, соответствуют значения l=0, 1, 2. 3 и т.д.
© ФГОУ ВПО Красноярский государственный аграрный университет, 2015
Волновая функция – математическая абстракция или физическая реальность?
Известно, что квантовые объекты могут вести себя странным образом: как будто они двигаются сразу в нескольких направлениях, находятся одновременно в нескольких местах или вращаются сразу по и против часовой стрелки. На математическом уровне квантовое поведение частиц описывается при помощи так называемой «волновой функции». В зависимости от условий эксперимента она позволяет рассчитать, например, вероятность нахождения электрона в определенном месте. Или предсказать (опять же в терминах вероятности), как будет направлен его спин – вверх или вниз.
Но математика не дает ответа на вопрос о природе этой функции. Является ли она элементом физического мира? Или это всего лишь математический инструмент, позволяющий нам работать в условиях фундаментального непонимания этого мира? И стоит ли вообще задаваться такими вопросами? Физики ставят эксперименты, чтобы понять природу этой загадочной функции, описывающей странности квантового мира.
Если бомбардировать редкими электронами стенку с двумя крошечными дырками, часть электронов проходит сквозь отверстия и каждый из них оставляет точечный след на экране за стенкой. Проводя эксперимент достаточное время, мы могли бы ожидать возникновение на экране двух круглых пятен, однако проявляющаяся картина выглядит более изощрённой и совпадает с картиной интерференции электромагнитных волн. Волновые свойства электрона и других элементарных частиц можно выразить математически через так называемую волновую функцию, определяющую вероятность обнаружить частицу в некоторой области пространства в течение заданного промежутка времени.
Да, наблюдения показывают и теории предсказывают, что квантовые объекты ведут себя странно, но имеет ли смысл думать о том, почему они так делают?
Здесь мнения ученых разделились. Сторонники так называемой «копенгагенской интерпретации» квантовой механики считают, что размышлять об этом не имеет практического смысла. Волновая функция – это работающий инструмент для предсказания результатов наблюдений. Суть этого подхода хлестко изложил Дэвид Мермин: «Заткнись и вычисляй!» И в целом эта позиция оправдана, поскольку привела к огромному прогрессу в ядерной физике и других отраслях.
Однако не всех ученых такой подход устраивает, и они продолжают предлагать свои интерпретации квантовых феноменов. Сторонники так называемой «причинной интерпретации», корни которой уходят к работам Эйнштейна, полагают наличие у квантовых объектов неких «скрытых параметров», знать которые нам пока не дано. Волновая функция отражает, таким образом, наше неведение относительно реального мира. На вопрос, жив или мертв кот Шредингера, сторонники причинной интерпретации отвечают: «Не знаю. Давайте поглядим». Однако есть и другие интерпретации, часть из которых рассматривают волновую функцию как элемент реальности. Одна из философских сложностей здесь состоит в том, что последние считают вышеупомянутого кота «одновременно» и живым, и мертвым, так же, как и приверженцы успешной копенгагенской интерпретации.
Кто же из них прав? На этот вопрос крайне сложно ответить при помощи эксперимента. Однако физику О. Мэруни и его коллегам из Оксфордского университета (Великобритания) удалось придумать эксперимент для проверки реальности волновой функции, а в прошлом году А. Федрицци, А. Уайт и др. (Квинслендский университет, Австралия) смогли реализовать его на практике. Суть эксперимента проста. Представьте две колоды карт – в одной карты только красной масти, а в другой одни тузы. «Вам дают карту и предлагают определить, из какой она колоды», – говорит физик М. Рингбауэр (Квинслендский университет). – «Если это красный туз, то вы имеете перекрывание (совмещение) признаков, и вы не сможете сказать, из какой эта карта колоды». Даже если вы знаете точный состав карт в каждой колоде, то в лучшем случае вы сможете подсчитать лишь вероятность возникновения такой неопределенной ситуации.
Подобная неопределенность присутствует и в квантовых системах. Экспериментаторы измерили поляризацию и другие параметры луча фотонов и обнаружили перекрывание, которое нельзя объяснить при помощи моделей, основанных на причинной интерпретации. Результаты эксперимента свидетельствуют о том, что если объективная реальность существует, то волновая функция реальна. С этим выводом можно спорить, потому что условия эксперимента предполагали существенные допущения. Поэтому ученые планируют в ближайшее время провести аналогичный эксперимент с ионами, которые легче отследить, чем фотоны. «В ближайшие полгода мы надеемся разработать эксперимент, не допускающий двойного толкования», говорит Мэруни.
В конечном счете такие исследования подводят нас вплотную к философскому вопросу о существовании объективной реальности. Хотя никто еще не знает, как это сделать, но, как говорит Уайт, «было бы невероятно интересно разработать эксперимент, чтобы проверить, существует ли на самом деле объективная реальность».
Подготовила Алла Кобкова
Проблема понимания и интерпретации квантового мира привлекает внимание ученых с первых лет развития квантовой механики. Нильс Бор утверждал, что наше сознание и язык не подходят для понимания явлений, происходящих на микро-масштабах. Квантовая механика смогла корректно предсказать исход тысяч экспериментов, что подтверждает ее статус как теории. Однако значительно сложнее проверить надежность ее интерпретаций. Один из наиболее интересных экспериментов в этой области поставил Ален Аспе в 1982 году – этот эксперимент показал отсутствие «скрытых параметров», которые могли бы определить результат квантовомеханических экспериментов, являющихся вероятностными с точки зрения современной физики. Проблема до сих остается скорее предметом философии нежели физики. В 1957 году Хью Эверетт разработал теорию множественности миров, согласно которой все альтернативные результаты измерений являются частью реальности, каждый в своем мире. Последние достижения квантовой оптики и компьютерного моделирования позволяют нам поставить в реальности классические мысленные эксперименты, предложенные Эйнштейном и Шредингером, что повышает интерес к основам квантовой механики.
Исследование «многомировой интерперетации» Эверетта – это важный и интересный шаг в этом направлении.
Большая Энциклопедия Нефти и Газа
Физический смысл волновой функции i трудно объяснить. Чем больше численное значение г / г в данной точке, тем больше вероятность нахождения электрона именно в этой точке. Поэтому электрон в принципе может находиться в любой точке атома. Таким образом, квантовая механика вовсе не пытается установить точное местонахождение и скорость движения электрона в какой-то определенный момент времени. Вместо этого квантовая механика пользуется понятием вероятности нахождения электрона в данной точке пространства атома. [1]
Физический смысл волновой функции заключается в том, что ее квадрат i i2 пропорционален вероятности нахождения электрона в элементарном объеме пространства. [2]
Из физического смысла волновой функции вытекает, что квантовая механика имеет статистический характер. Она не позволяет определить местонахождение частицы в пространстве или траекторию, по которой движется частица. С помощью волновой функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. [4]
При обсуждении физического смысла волновой функции ty было упомянуто, что она может быть комплексной и что в этом случае плотность вероятности есть произведение ty на ее комп-лесно-сопряженное значение г Л Это произведение всегда действительно. [7]
В соответствии с физическим смыслом волновой функции она должна быть конечной, непрерывной и однозначной, а также обращаться в нуль для тех мест пространства, где частица не может находиться. Например, при рассмотрении движения электрона в атоме должна становиться равной нулю на бесконечно большом расстоянии от ядра. [9]
В соответствии с физическим смыслом волновой функции она должна быть конечной, непрерывной и однозначной, а также обращаться в нуль для тех мест пространства, где частица не может находиться. Например, при рассмотрении движения электрона в атоме ф должна становиться равной нулю на бесконечно большом расстоянии от ядра. [10]
В соответствии с физическим смыслом волновой функции она должна быть конечной, непрерывной и однозначной, а также обращаться в нуль там, где частица не может находиться. Например, при рассмотрении движения электрона в атоме г э должна становиться равной нулю на бесконечно большом расстоянии от ядра. [11]
В соответствии с физическим смыслом волновой функции она должна быть конечной, непрерывной и однозначной, а также обращаться в нуль в тех местах пространства, где частица не может находиться. Например, для движущегося электрона в атоме функция ф должна становиться равной нулю на бесконечно большом расстоянии электрона от ядра. [12]
В соответствии с физическим смыслом волновой функции она должна быть конечной, непрерывной и однозначной, а также обращаться в нуль там, где частица не может находитьс я. [13]
Интерпретация физического смысла волновой функции
Вы будете перенаправлены на Автор24
Определение физического смысла волновой функции
$P=\psi \left(x,\ y,\ z\right)<\psi >^*\left(x,\ y,\ z\right)$ (2)
Ее абсолютные значения во всех точках должны быть такими, чтобы
Готовые работы на аналогичную тему
Способы представления волновой функции
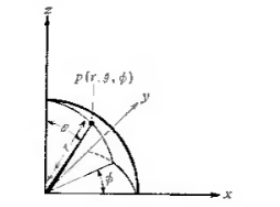
Рисунок 1. Система полярных координат
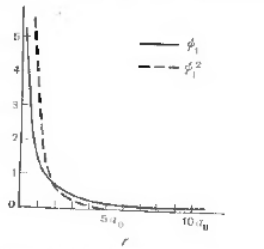
Рисунок 2. Графики волновых функций основного состояния атома водорода
Другой способ представления данной функции показан на рисунке 3. Этот рисунок можно интерпретировать несколькими способами:
Прежде всего, представим себе, что имеем очень большое число атомов водорода. В некоторый момент времени электроны в каждом атоме в общем будут находиться на разном расстоянии от ядра. Если изображения всех этих атомов наложить друг на друга, то получим картину, представленную на рис. 3.
Можно взять только один атом и наблюдать его много раз, по мере того, как электрон будет менять свое положение относительно ядра. Если затенить каждую маленькую область пространства пропорционально тому, как часто находится в нем электрон, то получится картина, показанная на рис. 3.
Можно вообще отказаться от изображения электрона как крошечного твердого тела, движущегося вокруг протона, и вместо этого рассматривать его как некоторое количество отрицательного заряда и массы, которая распределена или размазана вокруг ядра в соответствии с уравнением 2. В этом случае рисунок 3 представляет собой, грубо говоря, то, что можно было бы «увидеть» если бы можно было посмотреть на атом.
Рисунок 3. Представление волновой функции основного состояния атома водорода
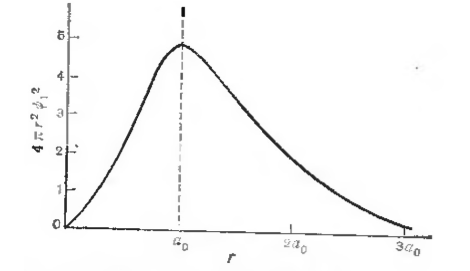
Рисунок 4. Функция плотности вероятности орбитали основного состояния атома водорода
Волновая функция
Вариант названия «амплитуда вероятности» связан со статистической интерпретацией волновой функции: вероятность нахождения частицы (или физической системы) в данном состоянии равна квадрату абсолютного значения амплитуды вероятности этого состояния.
Содержание
Физический смысл квадрата модуля волновой функции
зависит от координат (или обобщённых координат) системы и формируется таким образом, чтобы квадрат её модуля
представлял собой плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами

Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.
при любых комплексных 

Матричная и векторная формулировки
Любая функция может быть представлена, как бесконечная таблица из её значений, соответствующих каждому аргументу. Если представить в таком виде волновую функцию, то она станет столбцом координат бесконечномерного вектора в Гильбертовом пространстве, то есть, матрицей.
Одна и та же волновая функция в различных представлениях — будет соответствовать выражению одного и того же вектора в разных системах координат. Остальные операции с волновыми функциями так же будут иметь аналоги на языке векторов.
Функциональная (волновая), матричная и векторная формулировки математически эквивалентны.
Философский смысл волновой функции
Волновая функция представляет собой наиболее полное возможное описание квантовомеханической системы, за исключением, быть может, матрицы плотности, предложенной Л.Д.Ландау, с помощью которой можно описывать системы систем, что невозможно при использовании волновой функции (в случае обычной системы матрица плотности есть тот же квадрат модуля волновой фукнции) скоростей всех её частиц и это описание позволяло описать всё будущее и прошлое системы, то в квантовой механике некоторые параметры описать принципиально невозможно. Согласно квантовой механике, описание системы заканчивается на уровне волновой функции (и матрицы плотности) и только на уровне волновой функции (и матрицы плотности) возможно описать будущее и прошлое системы. Более подробное описание системы, например, с точностью до указания местоположений и скоростей всех её частиц — невозможно, и значения этих параметров оказываются более или менее случайными.
Следует понимать, что проблема, которую решает квантовая механика, — это проблема самой сути научного метода познания мира. Если представить себе бильярдный стол, закрытый непроницаемой крышкой, и единственным способом исследования вопроса, есть ли на нём бильярдные шары, предположить закатывание в стол других шаров, то мы и получаем ту самую проблему, для решения которой привлечён метод квантовой механики. Пока вброшенный шар проходит сквозь стол без изменения траектории, предсказуемо, мы можем сделать вывод о том, что на траектории шара других шаров нет. Если в результате взаимодействия шаров на столе мы получаем выкатившиеся несколько шаров с различными конечными импульсами и точками, в которых шары покинули стол, то мы можем лишь предполагать о том, каким образом происходило взаимодействие в системе. Если же лузы в бильярдном столе ограничивают возможность шаров покидать стол (энергетический барьер), то система запутывается ещё больше.
Подобный пример с бильярдом очень наглядно демонстрирует те трудности, с которыми сталкиваются исследователи, разрабатывая инструменты квантовой механики.
См. также
Выделить Волновая функция и найти в: