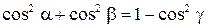в чем заключается физический принцип определения момента инерции методом колебаний

ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТЕЛ МЕТОДОМ КОЛЕБАНИЙ

Приборы и принадлежности: цилиндр на горизонтальной оси, шар на горизонтальной оси, секундомер.

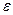
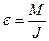
В динамике вращательного движения момент инерции играет ту же роль, что и масса в динамике поступательного движения: он определяет величину углового ускорения , получаемого телом под действием данного момента силы:

, (1)

где М – момент силы относительно оси вращения; 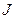– момент инерции относительно той же оси.

Величина момента инерции определяется не только массой тела, но и распределение той же массы относительно оси вращения. Одно и то же тело может иметь различные моменты инерции относительно разных осей, а тела различной массы при определенном распределении масс в них могут иметь одинаковые моменты инерции.

Момент инерции сплошного цилиндра относительно оси вращения совпадающей с его осью,

(2)

Момент инерции шара относительно оси, совпадающей с любым диаметром,

(3)

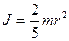
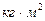
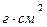
Момент инерции в системе СИ измеряется в , а в системе СГC – в . Момент инерции экспериментально можно определить различными способами. Один из них рассматривается в данной работе.

Описание экспериментальной установки и метода измерений

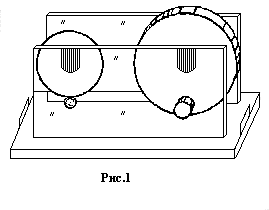
Прибор состоит из шара и цилиндра, которые могут вращаться вокруг горизонтальной оси с малым трением (рис. 3). Ось вращения проходит через центр тяжести исследуемого тела, которое находится в безразличном равновесии. Если к исследуемому телу прикрепить вспомогательный груз (вне оси вращения), то состояние безразличного равновесия системы заменится состоянием устойчивого равновесия. Если тело вывести из положения равновесия, то оно будет совершать колебания с некоторым периодом Т. Исследуемое тело с дополнительным грузом можно рассматривать как физический маятник, которым может быть любое твердое тело, подвешенное на оси, не проходящей через центр тяжести.

Дата добавления: 2015-08-01 ; просмотров: 1169 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Определение моментов инерции методом колебаний

Цель работы: экспериментально определить момент инерции однородного стержня относительно двух параллельных осей, результат сопоставить с теоремой Штейнера.

Теоретическое описание

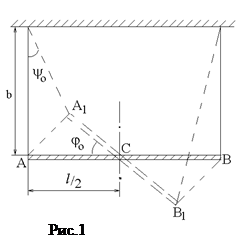
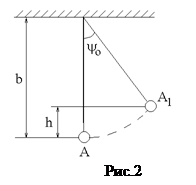
В данной работе методом колебаний определяем моменты инерции стержня относительно оси, проходящей через центр масс, J_c, и относительно параллельной ей оси, проходящей через конец стержня, J_A. Для определения момента инерции J_c наблюдаем малые колебания стержня на бифилярном подвесе (рис.1,2). Для определения момента инерции стержня J_A наблюдаем малые колебания, подвесив его за конец (рис.3).

За счет трения в точках подвеса энергия колебаний стержня уменьшается. Однако если ограничится наблюдением нескольких колебаний (в пределах 10-20 колебаний), то работа сил трения будет невелика, Ее можно не учитывать и при малых углах отклонения (6-8°) колебания считать гармоническими:

(1)

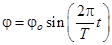
где j₀ – угловая амплитуда; T – период колебаний. Так как работой сил трения пренебрегаем, то полная механическая энергия стержня остается неизменной. При прохождении положения равновесия стержень обладает только кинетической энергией: 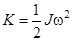, где w – максимальная угловая скорость.

При отклонении стержня от положения равновесия на максимальный угол его полная механическая энергия (потенциальная) U = mgh, где h – максимальная высота поднятия центра масс стержня.

Запишем закон сохранения энергии

(2)

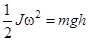
Формулы (1) и (2) позволяют найти момент инерции J, если измерен на опыте период колебаний T.

1. Определение J_c – момента инерции стержня относительно оси симметрии.

Стержень на бифилярном подвесе совершает крутильные колебания (см. рис.1). Определяем его максимальную угловую скорость w, продифференцировав (1) по времени:

; (3)

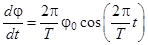
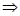
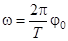
Максимальная высота подъема центра масс стержня определяется углом ψ₀ (см.рис.2):

,

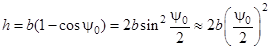
где b – длина нити подвеса; ψ₀ – максимальный угол отклонения нити, однозначно связанный с максимальным углом отклонения стержня от положения равновесия j₀. При малых значениях j₀ и ψ₀ конец стержня проходит путь AA₁, который приближенно можно считать равным длине дуги AA₁:

, .

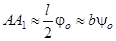
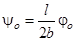
Теперь выразим h через угол φ_o:

(4)

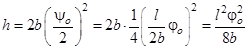
Подставляя (3) и (4) в (2), получаем

(5)

2. Определение J_A момента инерции стержня относительно оси, перпендикулярной ему и проходящей через конец.

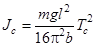
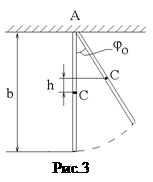
В формулу (2) подставляем соответствующие значения максимальной скорости при прохождении положения равновесия w из (3) и максимальной высоты поднятия центра масс h (рис.3). Из рис.3 получаем связь между h и углом j₀:

(6)

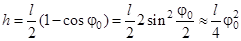
Из равенства (20) с учетом (3) и (6) получаем

(7)

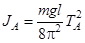
Таким образом, измеряя на опыте периоды колебаний стержня T_c и T_A, длину нити подвеса, длину стержня, можно вычислить моменты инерции J_c и J_A стержня относительно параллельных осей, а результат сопоставить с теоремой Штейнера.

Источник

Измерение момента инерции твердого тела методом крутильных колебаний

Момент инерции – это величина, характеризующая инертность тела при вращательном движении.

;

; (5.1)

.

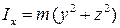
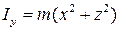
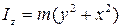
Момент инерции системы материальных точек относительно неподвижной оси равен сумме произведений массы каждой точки на квадрат расстояния до оси вращения

. (5.2)

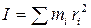
Тогда моменты инерции системы материальных точек относительно осей декартовой системы координат OX, OY и OZ равны

;

; (5.3)

.

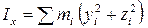
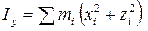
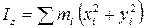
При определении момента инерции твердого тела его разбивают на достаточно большое число элементарных частей (элементарных масс) и представляют как систему большого числа материальных точек. Тогда момент инерции твердого тела I определяется по формуле (5.2), а моменты инерции I_x, I_y, I_z относительно осей декартовой системы координат равны соответствующим выражениям в (5.3).

Для более точного вычисления момента инерции сплошного твердого тела необходимо суммирование в (5.2) заменить интегрированием

, (5.4)

где dm=r dV, r – плотность тела в элементарном объеме dV; r – расстояние этого объема до оси вращения. Формулы (5.2)-(5.4) показывают, что момент инерции твердого тела зависит от распределения массы, формы тела, а также от расположения оси вращения.

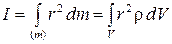
Если известен момент инерции I_c тела относительно некоторой оси, проходящей через центр масс, то можно определить момент инерции I относительно любой параллельной оси:

где m – масса тела; a – расстояние между параллельными осями. Это утверждение носит название теоремы Штейнера.

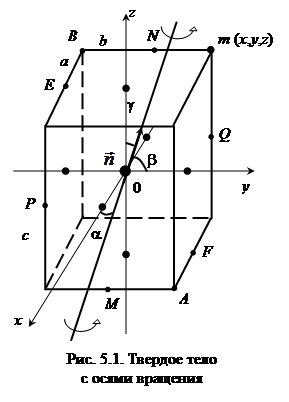
В настоящей работе измеряются моменты инерции однородных симметричных твердых тел куба и параллелепипеда относительно разных осей вращения. Введем для них прямоугольную систему координат OXYZ с началом в центре масс, оси которой совпадают с геометрическими осями симметрии тел (рис. 5.1). В такой системе координат для момента инерции твердого тела относительно любой оси вращения, проходящей через центр масс, выполняется равенство

, (5.5)

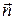
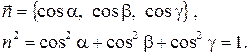
в котором – единичный вектор, определяющий направление оси вращения

(5.6)

Здесь a, b, g – углы между направлением вектора 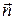и осями координат OX, OY, OZ (рис. 5.1); cos a, cos b, cos g – направляющие косинусы.

В работе для измерения моментов инерции твердого тела и проверки формулы (5.5) применяется метод крутильных колебаний. Схема экспериментальной установки изображена на рис. 5.2. Если свободную рамку 1 повернуть на некоторый угол j, то происходит закручивание проволоки, на которой она подвешена. Тогда силы упругости стремятся повернуть рамку в исходное положение. Момент M возвращающей силы при относительно малом угле поворота j связан с ним соотношением

, (5.7)

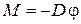
где D – коэффициент, называемый модулем кручения проволоки. Величина D зависит от длины проволоки, ее диаметра и модуля сдвига, характеризующего упругие свойства материала.

Запишем основной закон динамики вращательного движения для рамки

, (5.8)

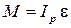
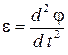
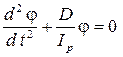
где – угловое ускорение; I_p – момент инерции рамки. Из формул (5.7) и (5.8) получаем дифференциальное уравнение движения рамки

, (5.9)

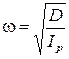
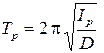
которое является уравнением колебаний с циклической частотой и периодом колебаний рамки

. (5.10)

Закрепим исследуемое твердое тело 4 в рамке 1 (рис. 5.2) так, чтобы одна из его геометрических осей симметрии совпала с осью вращения рамки. Теперь момент инерции крутильного маятника I_M равен сумме момента инерции образца I и момента инерции I_р рамки

. (5.11)

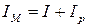
Запишем формулу для периода колебаний рамки с телом, аналогичную (5.10), и получим

. (5.12)

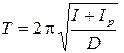
Исключая из (5.10) и (5.12) величину D, находим момент инерции тела

. (5.13)

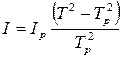
Формула (5.13) позволяет выразить момент инерции тела I относительно оси маятника через момент инерции I_p свободной рамки. Для этого надо измерить периоды колебаний T_p и T соответственно свободной рамки и для рамки с телом.

Период колебаний T, так же как и момент инерции тела (5.5), зависит от ориентации тела по отношению к оси маятника. Запишем (5.13) в виде

, (5.14)

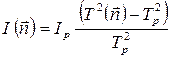
где 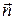– единичный вектор, направленный вдоль оси маятника.

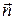
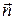
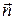
В лабораторной установке ось маятника (она же ось вращения тела) направлена по вертикали. Поэтому во всех опытах следует считать, что единичный вектор направлен вертикально вверх. Момент инерции тела относительно вертикальной оси, то есть I( ), измеряют, поворачивая тело и закрепляя его в различных положениях по отношению к этой оси (рис. 5.1). Направив оси OX, OY, OZ вдоль осей симметрии твердого тела, мы выбрали систему координат OXYZ, жестко связанную с ним. Поворачивая тело, мы изменяем направление вектора в жестко связанной с телом системе координат OXYZ.

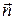
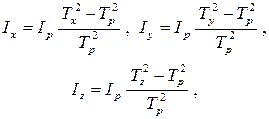
Закрепим тело в рамке так, чтобы ось вращения совпала с какой-либо осью OX, OY, OZ. Тогда из (5.14) получим

. (5.15)

где T_x, T_y, T_z – соответственно периоды колебаний маятника, когда ось его вращения 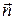совпадает с одной из осей OX, OY или OZ.

Подставив (5.14) и (5.15) в исходное соотношение (5.5), получим для квадрата периода равенство

. (5.16)

Таким образом определяется связь между периодами крутильных колебаний тела T_x, T_y, T_z относительно его осей симметрии OX, OY, OZ и периодом колебаний этого же тела относительно оси 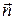с направляющими косинусами cos a, cos b и cos g. Формула (5.16) удобна тем, что все входящие в нее величины в условиях эксперимента могут быть измерены непосредственно.

Период колебаний T – это продолжительность одного полного колебания. Величину T можно измерить как время между двумя последовательными прохождениями рамкой положения равновесия в одном и том же направлении. Для повышения точности измерений T его находят, измеряя длительность t некоторого числа N полных колебаний, тогда

. (5.17)

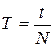
Рассмотрим исследуемые твердые тела в форме куба и прямоугольного симметричного и несимметричного параллелепипедов.

Однородный куб. Все три момента инерции куба относительно осей OX, OY и OZ одинаковые I_x=I_y=I_z. Из формулы (5.5) с учетом равенства (5.6) находим

. (5.18)

Таким образом, моменты инерции однородного куба относительно любых осей, проходящих через его центр, одинаковы. Период крутильных колебаний куба также должен быть одинаковым для любой оси вращения, проходящей через его центр: 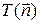=T_z=const. Это утверждение доказывается, если (5.18) подставить в (5.15) и найти Т_x, Т_y, Т_z., а затем воспользоваться формулой (5.16). Проверить его можно также экспериментально, закрепив куб в рамке в различных положениях, при которых ось вращения проходит через центр куба, и измерив соответствующие периоды крутильных колебаний.

Симметричный прямоугольный параллелепипед. В этом случае два момента инерции параллелепипеда относительно осей OX и OY и соответствующие им периоды крутильных колебаний равны между собой: I_x=I_y, T_x=T_y. Из (5.5) и (5.16) с учетом равенства

, (5.19)

. (5.20)

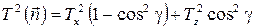
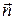
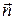
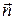
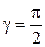
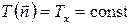
Таким образом, период крутильных колебаний T( ) зависит только от угла g, который ось вращения образует с осью тела OZ. Величина T( ) не зависит от углов a и b (при g=const). В частности, должен быть одинаковым период колебаний относительно любой оси, лежащей в плоскости OXY (то есть при ). В этом случае cos g=0 и, согласно (5.20), . Проверить это соотношение можно, закрепляя в рамке крутильного маятника симметричный параллелепипед так, чтобы ось вращения была перпендикулярна его большому ребру. Периоды крутильных колебаний при любом таком положении тела должны совпадать.

Несимметричный параллелепипед. Такой параллелепипед имеет относительно осей OX, OY, OZ три разных периода крутильных колебаний Т_x, Т_y и Т_z.

Закрепим параллелепипед в рамке так, чтобы ось вращения совпала с его главной диагональю АВ (рис. 5.1). Вычислив направляющие косинуса cos a, cos b и cos g, из (5.16) находим

. (5.21)

Аналогично для осей EF, MN и PQ из (5.16) следует

(5.22)

Таким образом, для проверки формулы (5.16) в случае несимметричного параллелепипеда необходимо выяснить, выполняются ли соотношения(5.21) и (5.22) для измеренных значений периодов колебаний.

Источник

Физический смысл момента инерции: аналогия с линейным движением, примеры

Любая физическая величина, которая предлагается в математических уравнениях при изучении того или иного явления природы, несет некоторый смысл. Не является исключением из этого правила и момент инерции. Физический смысл этой величины подробно рассмотрен в данной статье.

Момент инерции: математическая формулировка

В первую очередь следует сказать, что рассматриваемая физическая величина используется для описания систем вращения, то есть таких движений объекта, которые характеризуются круговыми траекториями вокруг некоторой оси или точки.

Приведем математическую формулу момента инерции для материальной точки:

Это выражение справедливо всегда, причем не только для трехмерных, но и для двумерных (одномерных) тел, то есть для плоскостей и стержней.

Из этих формул трудно понять смысл физический момента инерции, однако можно сделать важный вывод: он зависит от распределения массы в теле, которое вращается, а также от расстояния до оси вращения. Причем зависимость от r является более резкой, чем от m (см. знак квадрата в формулах).

Движение по окружности

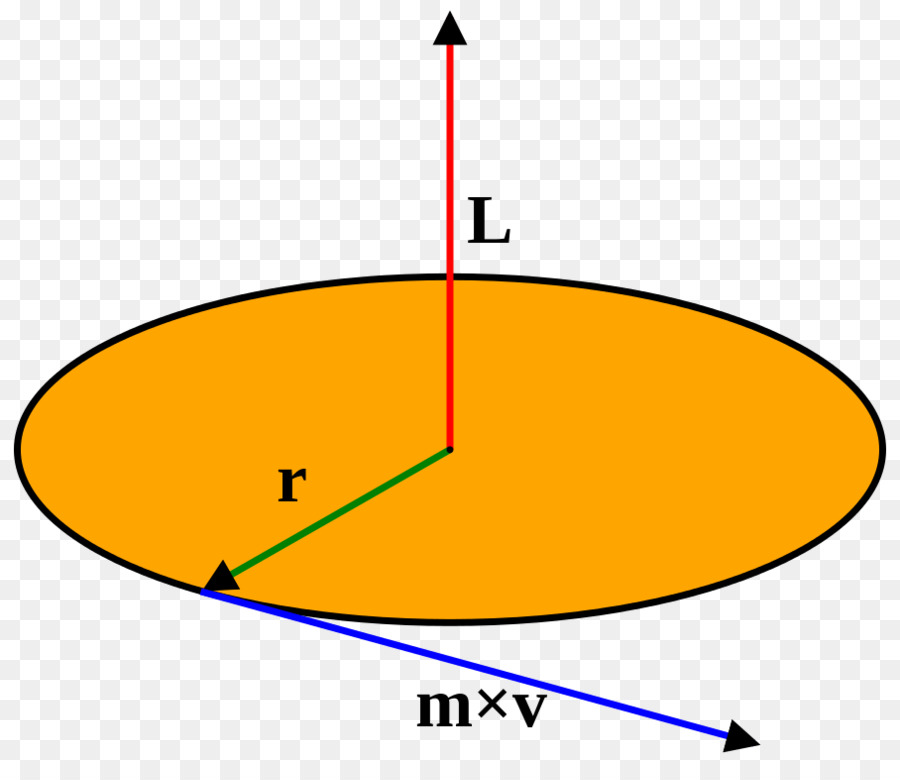
Понять, каков физический смысл момента инерции, невозможно, если не рассмотреть круговое движение тел. Не вдаваясь в подробности, приведем сразу два математических выражения, описывающих вращение:

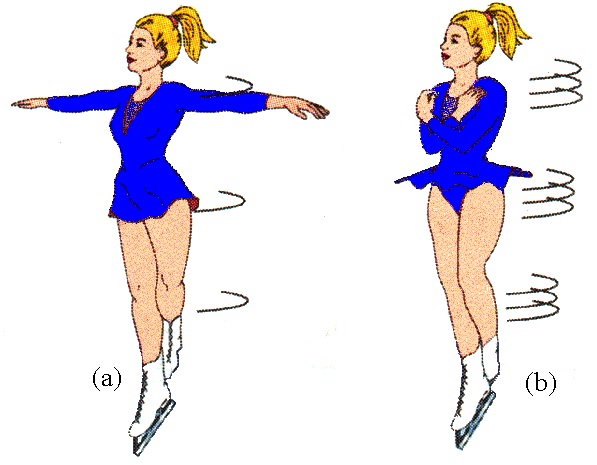
Верхнее уравнение носит название закона сохранения величины L (момента импульса). Оно означает, что какие бы изменения ни происходили внутри системы (сначала был момент инерции I1, а затем он стал равным I2), произведение I на угловую скорость ω, то есть момент импульса, будет оставаться неизменным.

Нижнее выражение демонстрирует изменение скорости вращения системы (dω/dt) при воздействии на нее некоторого момента силы M, который имеет внешний характер, то есть порождается силами, не связанными с внутренними процессами в рассматриваемой системе.

И в верхнем, и в нижнем равенствах присутствует I, причем чем больше ее значение, тем меньше будет угловая скорость ω или угловое ускорение dω/dt. В этом и заключается физический смысл момента инерции тела: он отражает способность системы сохранять свою угловую скорость. Чем больше I, тем сильнее проявляется эта способность.

Аналогия с линейным импульсом

Теперь перейдем к тому же выводу, что был озвучен в конце предыдущего пункта, проведя аналогию между вращательным и поступательным движениями в физике. Как известно, последнее описывается следующей формулой:

Теперь рассмотрим 2-й закон Ньютона, который выражается формулой:

Какой смысл несет масса в классической механике? Она является мерой инерции: чем больше m, тем труднее сдвинуть предмет с места, а тем более придать ему ускорение. То же самое можно сказать и о моменте инерции применительно к движению вращения.

Физический смысл момента инерции на бытовом примере

Кстати, описанный факт экспериментально проверили наши предки еще в стародавние времена, когда научились добывать огонь. Они раскручивали палочку с огромными угловыми ускорениями, что приводило к созданию больших сил трения и, как следствие, к выделению значительного количества теплоты.

В завершение хотелось бы привести, пожалуй, самый важный для современной техники пример использования физического смысла момента инерции. Маховик авто представляет собой сплошной стальной диск, имеющий относительно большие радиус и массу. Эти две величины обуславливают существование значительной величины I, характеризующей его. Маховик призван «смягчать» любые силовые воздействия на коленвал автомобиля. Импульсивный характер действующих моментов сил от цилиндров двигателя на коленвал сглаживается и делается плавным благодаря тяжелому маховику.

Кстати, чем больше момент импульса, тем больше энергии находится во вращающейся системе (аналогия с массой). Этот факт хотят использовать инженеры, запасая энергию торможения авто в маховике, чтобы впоследствии направить ее на разгон транспортного средства.

Источник