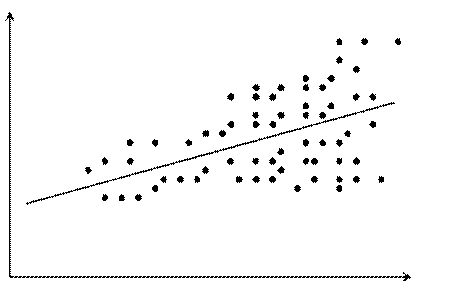
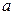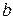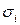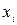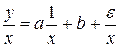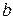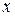в чем условие гетероскедастичности в регрессионной модели временного ряда если

Графики гетероскедастичности

В соответствии с одной из предпосылок МНК нужно, чтобы дисперсия остатков была гомоскедастичной. Это означает, что для каждого значения фактора X остатки е, имеют одну и ту же дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно продемонстрировать на поле корреляции (см. рис.).

Гомоскедастичность остатков означает, что дисперсия остатков одна и та же для каждого значения X. Используя трехмерное изображение, можно получить следующие графики, которые проиллюстрируют гомо- и гетероскедастичность

Рисунок с гомоскедастичностью показывает, что для каждого значения Х, распределения остатков одинаково в отличие от гетероскедастичности.

Для множественной регрессии вид графиков является наиболее наглядным способом изучения гомо- и гетероскедастичности.

Наличие гетероскедастичности может в ряде случаях привести к смещенности оценок коэффициентов регрессии, хотя несмещенность оценок коэффициентов регрессии, как правило, зависит от соблюдения второй предпосылки МНК, т. е. независимости остатков и величин факторов. Гетероскедастичность будет сказываться на уменьшении эффективности оценок b. В ча-стности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии Sb, которая предполагает единую дисперсию остатков для любых значений фактора.

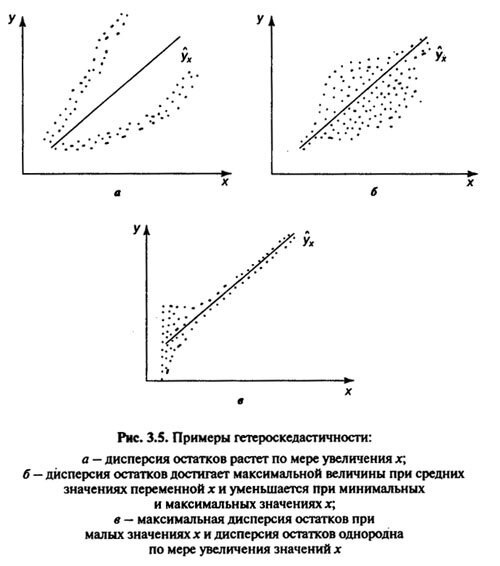
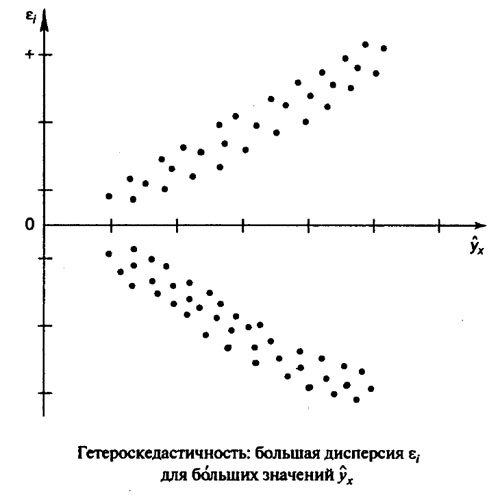
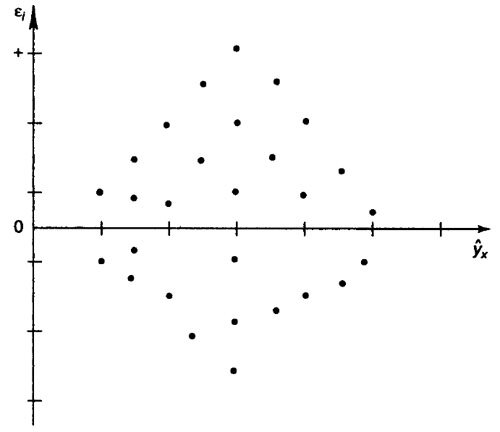
Определение гетероскедастичности

При малом объеме выборки, что характерно для большинства задач эконометрики, для оценки гетероскедастичости используют метод Гольдфельда — Квандта, который был разботан в 1965 г. Гольдфельдом и Квандтом, где они рассмотрели однофакторную линейную модель, для которой дисперсия остатков возрастает пропорционально квадрату фактора. Чтобы оценить нарушение гомоскедастичности, они предложили выполнить следующие операции.

При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять критерию Фишера с (n — С — 2p) : 2 степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F-критерия, тем в большей степени нарушена предпосылка о равенстве дисперсий остаточных величин.

Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.

Для перехода на страницу решения контрольных по эконометрике жмите сюда

Источник

Ответы на экзаменационные билеты по эконометрике.

57. Гетероскедастичность остатков модели регрессии.

Случайной ошибкой называется отклонение в линейной модели множественной регрессии:

В связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается выборочная оценка случайной ошибки модели регрессии по формуле:

Где еi – остатки модели регрессии.

Термин гетероскедастичность в широком смысле понимается как предположение о дисперсии случайных ошибок модели регрессии.

При построении нормальной линейной модели регрессии учитываются следующие условия, касающиеся случайной ошибки модели регрессии:

6) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

7) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:

8) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):

Означает гомоскедастичность (hоmоsсеdаstiсitу – однородный разброс) дисперсий случайных ошибок модели регрессии.

Под гомоскедастичностью понимается предположение о том, что дисперсия случайной ошибки βi является известной постоянной величиной для всех наблюдений.

Но на практике предположение о гомоскедастичности случайной ошибки βi или остатков модели регрессии еi выполняется не всегда.

Под гетероскедастичностью (hеtеrоsсеdаstiсitу – неоднородный разброс) понимается предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, что означает нарушение второго условия нормальной линейной модели множественной регрессии:

Гетероскедастичность можно записать через ковариационную матрицу случайных ошибок модели регрессии:

Тогда можно утверждать, что случайная ошибка модели регрессии βi подчиняется нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2Ω:

Где Ω – матрица ковариаций случайной ошибки.

Если дисперсии случайных ошибок.

Модели регрессии известны заранее, то проблема гетероскедастичности легко устраняется. Однако в большинстве случаев неизвестными являются не только дисперсии случайных ошибок, но и сама функция регрессионной зависимости у=f(х), которую предстоит построить и оценить.

Для обнаружения гетероскедастичности остатков модели регрессии необходимо провести их анализ. При этом проверяются следующие гипотезы.

Основная гипотеза Н0 предполагает постоянство дисперсий случайных ошибок модели регрессии, т. е. присутствие в модели условия гомоскедастичности:

Альтернативная гипотеза Н1 предполагает непостоянство дисперсиий случайных ошибок в различных наблюдениях, т. е. присутствие в модели условия гетероскедастичности:

Гетероскедастичность остатков модели регрессии может привести к негативным последствиям:

1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности;

2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.

Источник

ОТветы на синергию. Эконометрика. Автокорреляционная функция это функция от Тип ответа

Модель авторегрессии первого порядка

Обобщенный метод наименьших квадратов

Постоянство дисперсии случайного члена регрессионного уравнения

Отсутствие зависимости между остатками текущих и предыдущих наблюдений

Процесс не является стационарным в широком смысле

Показатель, характеризующий тесноту линейной стохастической связи между переменными

Явление линейной стохастической связи между переменными

Показатель, позволяющий установить факт наличия линейной

стохастической связи между переменными

Дисперсии зависимой переменной, объясняемую регрессией в общей ее дисперсии

Процентное изменение зависимой переменной при однопроцентном изменении независимой переменной

Статистической значимости модели в целом

Статической зависимости каждого из коэффициентов модели

Определения статической значимости каждого коэффициента уравнения

Наличие линейной зависимости между несколькими объясняющими переменными

Дисперсии коэффициентов регрессии

Числа структурных коэффициентов над числом приведенных

О мультиколлинеарности факторов

Значение коэффициента равно нулю

С ростом Х происходит убывание У

Объясняющей переменной в i-м наблюдении и прогнозным значением этой переменной

Ранговое условие и порядковое условие со знаком равенства

Коэффициенты множественной детерминации некоторых объясняющих факторов с остальными

Переменной Y в i-м наблюдении и прогнозным значением этой переменной, полученным по выборочной линии регрессии

Положительные и отрицательные

Эндогенных переменных минус единица

Отбор факторов, влияющих на результат и выбор вида уравнения

Парные и множественные

Необходимым и достаточным

Системы минус единица

Процентное изменение зависимой переменной при однопроцентном изменении независимой переменной

Проверки статистической значимости фактора

Можно рассматривать в узком и в широком смысле

Характеристика временного ряда, связанная с его стабильностью

Качество уровня регрессии в целом

По нормальному закону

Качество уравнения регрессии в целом

Ее математическое ожидание не равно ей

Связь между переменными, сложенная влиянием случайных факторов

Обладают свойством гетероскедастичности

Источник

Проблема гетероскедастичности

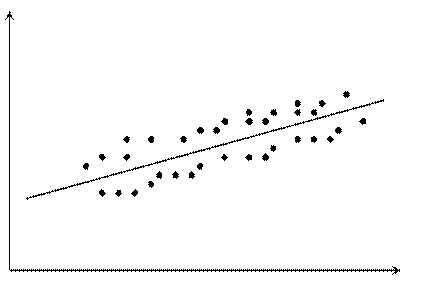
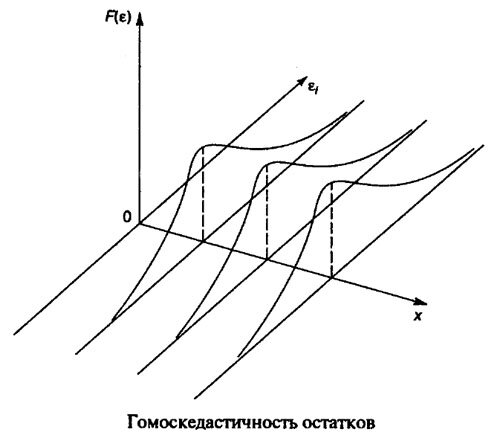
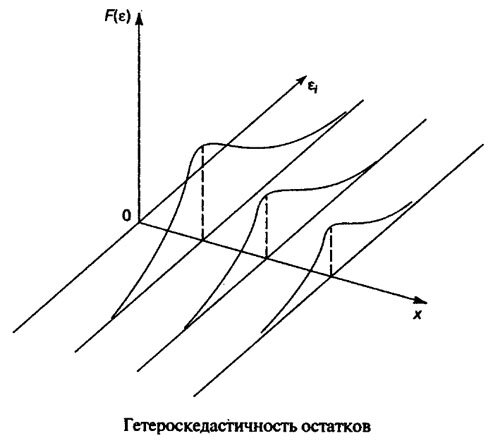
Предположение о постоянстве и конечности дисперсии остатков называется свойством гомоскедастичности остатков (рисунок 5.1). В практических исследованиях это свойство случайной ошибки модели регрессии не всегда выполняется и дисперсия остатков не является постоянной величиной (рисунок 5.2). Такое явление называется гетероскедастичностью.

Рис. 5.1. Линейная модель с гомоскедастичностью

Гетероскедастичность часто вызывается ошибками спецификации, когда не учитывается в модели существенная переменная.

Гетероскедастичность приводит к тому, что оценки коэффициентов регрессии не являются эффективными, т.е. их дисперсии не будут наименьшими. Как следствие рассчитанные значения стандартных ошибок коэффициентов регрессии могут быть заниженными, а потому при проверке статистической значимости коэффициентов может быть ошибочно принято решение об их значимом отличии от нуля, тогда как на самом деле это не так.

Проблема гетероскедастичности характерна для пространственных данных, полученных от неоднородных объектов. Например, если исследуется зависимость расходов на питание в семье от ее общего дохода, то можно ожидать, что разброс данных будет выше для семей с более высоким доходом. Если исследуется зависимость оплаты труда сотрудников предприятий в зависимости от размера основных фондов предприятий и разряда работника, то понятно, что вариация оплаты труда на крупных предприятиях у сотрудников высокого разряда будет значительно превосходить его вариацию для сотрудников низких уровней на малых и средних предприятиях.

Гетероскедастичность иногда возникает и во временных рядах. Это происходит в тех случаях, когда зависимая переменная имеет большой интервал качественно неоднородных значений или высокий темп изменения (инфляция, технологические сдвиги, изменения в законодательстве, потребительские предпочтения и т.д.).

Рис. 5.2. Линейная модель с гетероскедастичностью

В настоящее время для оценки нарушения гомоскедастичности предложено большое число тестов. Чаще всего используются графический анализ отклонений, тест ранговой корреляции Спирмена и тест Голдфелда-Квандта.

Графический анализ отклонений заключается в визуальной оценке разброса точек корреляционного поля около линии регрессии: считается, что условие 2 выполняется, если точки наблюдений расположены внутри полосы постоянной ширины, окаймляющей линию регрессии (например, как на рисунке 5.1). Для множественной регрессии осуществляется графический анализ корреляционных полей объясняемой переменной в зависимости от каждого из факторов .

Наиболее популярным тестом обнаружения гетероскедастичности является тест Голдфелда-Квандта. Тест применяется в том случае, если ошибки регрессии можно считать нормально распределенными случайными величинами. Кроме того, в основе его лежит предположение о пропорциональности дисперсий случайного члена значению выбранной объясняющей переменной. Тест проводится по следующей схеме.

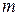
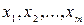
1. На основе выборочных данных строится линейная модель множественной регрессии с объясняющими переменными .

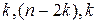
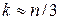
2. В модели множественной регрессии (например, на основе графического анализа) выбирается факторная переменная, от которой предположительно могут зависеть остатки. Значения этой переменной ранжируются, располагаются по возрастанию и делятся на три части объемами (обычно принимают ).

3. Для первой и третьей частей строятся две независимые модели регрессии.

4. По каждой из построенных моделей рассчитывают суммы квадратов остатков S₁ и S₃.

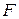
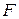
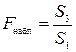
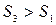
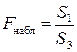
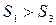
5. Осуществляется проверка основной гипотезы об отсутствии гетероскедастичности с помощью -критерия Фишера. Наблюдаемое значение -критерия рассчитывается следующим образом:

, если ,

, если .

Если , то в основной модели присутствует гетероскедастичность, зависящая от выбранной объясняющей переменной (число степеней свободы определяется значениями и ).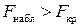

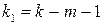
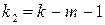
Если нет уверенности относительно выбора объясняющей переменной, вызывающей гетероскедастичность, то тест осуществляется для каждой из объясняющих переменных .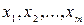

Наличие гетероскедастичности в остатках регрессии можно проверить и с помощью теста ранговой корреляции Спирмена. При выполнении теста предполагается, что абсолютные величины остатков и значения объясняющей переменной коррелированны. Эту корреляцию можно измерять с помощью коэффициента ранговой корреляции Спирмена:

,

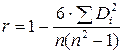
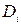
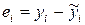
где – разность между рангом и рангом модуля остатка .

Тест проводится по следующей схеме.

1. Строится линейная модель регрессии.

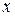
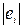
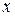
2. Данные по и модули остатков ранжируются по переменной , определяются их ранги (ранг – это порядковый номер значений переменной в ранжированном ряду).

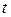
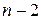
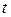
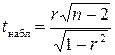
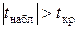
3. Осуществляется проверка основной гипотезы об отсутствии гетероскедастичности с помощью -статистики с степенями свободы, где n – объем выборки. При этом наблюдаемое значение -критерия определяется равенством . Если , то нулевая гипотеза об отсутствии гетероскедастичности отклоняется и имеет место гетероскедастичность в остатках регрессии, т.е. условие 2 не выполняется.

После установления в модели наличия гетероскедастичности возникает вопрос о том, в какой мере существенно она влияет на качество модели и следует ли вообще с гетероскедастичностью бороться. Ведь при гетероскедастичности оценки коэффициентов регрессии все равно остаются несмещенными и состоятельными, правда, не будут эффективными.

Если исследователь решил вступить в борьбу с гетероскедастичностью, то первый шаг на этом пути заключается в определении ее типа. Если гетероскедастичность вызвана ошибками спецификации, то для ее устранения необходимо включить в уравнение пропущенные существенные переменные и подобрать правильную функциональную форму. Если гетероскедастичность наблюдается в правильно специфицированных моделях (чистая гетероскедастичность), то можно воспользоваться взвешенным методом наименьших квадратов (ВМНК).

Данный метод применяется при известных для каждого наблюдения значениях дисперсиях 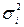. В этом случае можно устранить гетероскедастичность, разделив каждое наблюдаемое значение на соответствующее ему среднеквадратическое отклонение. Тем самым обеспечивается равномерный вклад остатков в общую сумму.

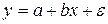
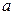
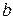
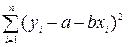
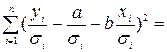
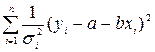
Таким образом, если при обычном МНК в случае парной линейной модели для нахождения ее параметров и минимизируется сумма , то при ВМНК минимизируется сумма

.

Применение ВМНК включает следующие этапы.

1. С помощью обычного МНК строится линейная регрессионная модель и

доказывается наличие гетероскедастичности остатков.

2. Для каждого наблюдения устанавливаются фактические значения дисперсий 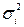отклонений.

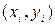
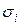
3. Значения каждой пары наблюдений делятся на известную величину . Тем самым наблюдениям с наименьшими дисперсиями придаются наибольшие веса, а наблюдениям с наибольшими дисперсиями – наименьшие веса.

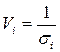
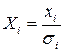
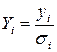
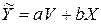
4. С помощью обычного МНК по преобразованным значениям , , (такое преобразование называется масштабированием исходных данных) оценивается двухфакторное уравнение регрессии с нулевым свободным членом. Построенная модель гомоскедастична.

Описанный подход возможен и для уравнения множественной регрессии.

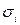
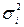
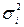
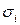
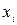
Главная проблема взвешенного метода наименьших квадратов состоит в необходимости знания среднеквадратических отклонений случайных ошибок регрессии. На практике дисперсии неизвестны. В таком случае делаются реалистические предположения об их величине. В частности, принимаются предположения о том, что либо дисперсии отклонений, либо сами среднеквадратичные отклонения пропорциональны значениям переменной .

Следует иметь в виду, что коэффициенты и модели оценены по преобразованным данным, а потому изменяют свой первоначальный экономический смысл. В частности, если среднеквадратичные отклонения пропорциональны значениям , то обычным МНК оценивается преобразованная модель , в которой по сравнению с исходной моделью свободный член и угловой коэффициент как бы поменялись местами. Поэтому оценка свободного члена преобразованной модели характеризует изменение показателя при изменении фактора на одну единицу.

Источник