в чем суть теории пуанкаре
О гипотезе Пуанкаре. Лекция в Яндексе
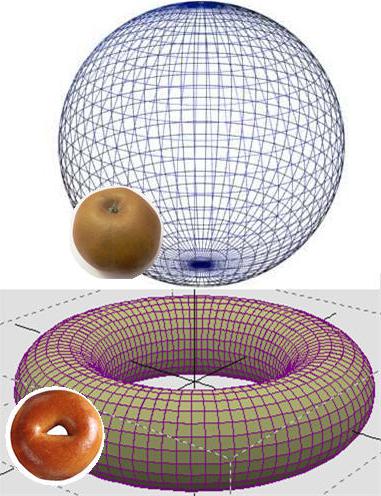
Еще в XIX веке было известно, что если любую замкнутую петлю, лежащую на двумерной поверхности, можно стянуть в одну точку, то такую поверхность легко превратить в сферу. Так, поверхность воздушного шарика удастся трансформировать в сферу, а поверхность бублика – нет (легко вообразить себе петлю, которая в случае с бубликом не стянется в одну точку). Гипотеза, высказанная французским математиком Анри Пуанкаре в 1904 году, гласит, что аналогичное утверждение верно и для трехмерных многообразий.
Доказать гипотезу Пуанкаре удалось только в 2003 году. Доказательство принадлежит нашему соотечественнику Григорию Перельману. Эта лекция проливает свет на объекты, необходимые для формулировки гипотезы, историю поиска доказательства и его основные идеи.
Читают лекцию доценты механико-математического факультета МГУ к. ф-м. н. Александр Жеглов и к. ф.-м. н. Федор Попеленский.
Если не вдаваться в математические подробности, то вопрос, поднимаемый гипотезой Пуанкаре можно следующим образом: как охарактеризовать (трехмерную) сферу? Чтобы правильно понять этот вопрос, нужно познакомиться с одним из важнейших понятий в топологии – гомеоморфизмом. Разобравшись с ним, мы сможем точно сформулировать гипотезу Пуанкаре.
Чтобы совсем уж не залезать в математические подробности формального определения, мы скажем, что две фигуры считаются гомеоморфными, если можно установить такое взаимно-однозначно соответствие между точками этих фигур, при котором близким точкам одной фигуры соответствуют близкие точки другой фигуры и наоборот. Пропущенные нами подробности состоят как раз в адекватной формализации близости точек.
Легко понять, что две фигуры гомеоморфны, если одну из другой можно получить произвольной деформацией, при которой запрещено «портить» поверхности (рвать, сминать области в точку, делать дырки и т.п.).
Например, чтобы получить из диска полусферу, как показано на картинке выше, нам потребуется просто нажать сверху в его центр, придерживая внешний обод. Можно представлять себе, что поверхности сделаны из идеальной резины, так что все фигуры могут сжиматься и растягиваться как угодно. Нельзя делать только две вещи: разрывать и склеивать.
Более точное (но все же не окончательное с точки зрения строгости) представление о гомеоморфных фигурах мы будем иметь, если разрешим еще одну операцию: можно сделать на фигуре разрез, перекрутить, завязать, развязать и т.п., но потом обязательно заклеить разрез как было.
Приведем еще один пример. Представим себе яблоко, в котором червяк прогрыз ход в виде узла и небольшую пещеру.
С точки зрения топологии поверхность этого яблока все равно останется сферой, т.к. если стянуть все это определенным образом, мы получим поверхность яблока в том же виде, как было до того, как червяк начал его есть.
Для закрепления попробуйте классифицировать буквы латинского алфавита с точностью до гомеоморфизма (т.е. выясните, какие буквы гомеоморфны, а какие — нет). Ответ зависит начертания букв (от типа шрифта или от гарнитуры), и для простейшего варианта начертания он приведен на следующем рисунке:
Из 26 букв у нас получается всего 8 классов.
На следующей картинке изображены гиря, кофейная чашка, бублик, сушка и кренделек. С топологической точки зрения поверхности гири, кофейной чашки, бублика и сушки одинаковы, т.е. гомеоморфны. Что касается кренделька, то он приведен здесь для сравнения с поверхностью, которую в топологии часто называют кренделем (он изображен в правом нижнем углу рисунка). Как вы, наверное, уже понимаете, и топологический крендель, и съедобный крендель отличаются от тора.
Формальная постановка вопроса
Пусть M – замкнутое связное многообразие размерности 3. Пусть на нем любая петля может быть стянута в точку. Тогда M гомеоморфно трехмерной сфере.
Наибольшую трудность для неподготовленного человека здесь вызывает понятие «многообразия размерности 3» и свойства, выраженные словами «замкнутое» и «связное». Поэтому мы попробуем разобраться со всеми этими понятиями и свойствами на примере размерности 2, в этом случаем многое кардинально упрощается.
Гипотеза Пуанкаре для поверхностей
Пусть M – замкнутая связная поверхность (многообразие размерности 2). Пусть на ней любая петля может быть стянута в точку. Тогда поверхность M гомеоморфна двумерной сфере.
Сначала определим, что такое поверхность. Возьмем конечный набор многоугольников, разбиваем все их стороны (ребра) на пары (т.е. всего сторон у всех многоугольников должно быть четное число), в каждой паре выбираем, каким из двух возможных способов будем их склеивать. Склеиваем. В результате поучается замкнутая поверхность.
Если полученная поверхность состоит из одного куска, а не из нескольких отдельных, то говорят, что поверхность связна. С формальной точки зрения это значит, что после склейки из любой вершины любого многоугольника можно по ребрам пройти в любую другую вершину.
Вот простой пример: если считать, что на картинке выше все треугольники правильные, то после склеивания у нас должен получиться правильный тетраэдр, поверхность которого также гомеоморфна сфере.
Формально нужно требовать, чтобы из любой вершины любого многоугольника после склейки можно было пройти в любую вершину любого многоугольника (по ребрам).
Нетрудно сообразить, что связную поверхность можно склеить и из одного многоугольника. На рисунке видна идея, как это обосновывается:
Рассмотрим примеры простейших склеек:
В первом случае у нас получится сфера:
Во втором случае у нас получится тор (поверхность бублика, мы встречались с ним раньше):
В третьем случае получится так называемая бутылка Клейна:
Если склеивать не все стороны многоугольника, то получится поверхность с краем:
Важно отметить, что после склейки «шрамы» от нее носят чисто «косметический характер. Все точки поверхности равноправны: у любой точки имеется окрестность гомеоморфная диску.
Две поверхности считаются гомеоморфными, если схемы склейки каждой из них можно так разрезать на схемы склейки из более мелких многоугольников, что схемы склейки станут одинаковыми.
Разберем это утверждение на примере разбиения поверхности куба на части, из которых можно сложить развертку тетраэдра:
Верен и более общий факт: поверхности всех выпуклых многогранников – это сферы.
Теперь подробнее остановимся на понятии петли. Петял — это замкнутая кривая на рассматриваемой поверхности. Две петли называются гомотопными, если одну из них можно продеформировать в другую без разрывов и склеек, оставаясь на поверхности. Ниже приведен простейший случай стягивания петли на плоскости или сфере:
Даже если петля на плоскости или сфере имеет самопересечения, ее все равно можно стянуть:
На плоскости можно стянуть любую петлю:
А вот какие петли бывают на торе:
Стянуть такие петли невозможно. (К сожалению, доказательство выходит довольно далеко за рамки нашего рассказа.) Более того, показанные петли на торе не гомотопны. Предлагаем слушателям или читателям найти еще одну петлю на торе, не гомотопную этим двум — это очень простой вопрос. После этого попробуйте найти на торе четвертую петлю, не гомотопную этим трем — это будет несколько сложнее.
Эйлерова характеристика
Теперь, когда мы познакомились со всеми основными понятиями из формулировки гипотезы Пуанкаре, попробуем приступить к доказательству двумерного случая (лишний раз отметим, что это многократно проще трехмерного случая). А поможет нам в этом эйлерова характеристика.
Эйлеровой характеристикой поверхности M назовем число B−P+Г. Здесь Г — число многоугольников, Р — это число ребер после склейки (в случае рассматриваемых поверхностей это половина числа сторон всех многоугольников), B — это число вершин, которое получается после склейки после склейки.
Если две схемы склейки задают гомеоморфные поверхности, то у этих схем числа B−P+Г одинаковы, т. е. B−P+Г является инвариантом поверхности.
Если поверхность уже как-то задана, то надо нарисовать на ней какой-нибудь граф, чтобы после разрезания по нему поверхность распалась на куски гомеоморфные дискам (например, кольца запрещены). Затем подсчитываем величину B−P+Г — это и есть эйлерова характеристика поверхности.
Будут ли гомеоморфны поверхности с одинаковыми эйлеровыми характеристиками, мы узнаем позже. Но совершенно точно можно утверждать, что если эйлеровы характеристики у поверхностей разные, то поверхности не гомеоморфны.
Знаменитое соотношение B−P+Г=2 для выпуклых многоугольников (теорема Эйлера) является частным случаем этой теоремы. В данном случае речь идет о конкретной поверхности — о сфере. Замечание Обозначение: Эйлерову характеристику поверхности M будем обозначать через χ(M): χ(M) = B − P + Γ
Если поверхность M связна, то χ(M) ≤ 2, причем χ(M) = 2 тогда и только тогда, когда M гомеоморфна сфере.
Посмотрев лекцию до конца, вы узнаете, как же все-таки доказывается гипотеза Пуанкаре в размерности 2, и как Григорию Перельману удалось доказать ее в размерности 3.
Гипотеза Пуанкаре: история проблемы, доказательство, смысл
По школьному курсу каждый знаком с понятиями теоремы и гипотезы. Как правило, в жизни затрагиваются самые простые и примитивные законы, в то время как математики делают очень сложные предположения и ставят интересные проблемы. Далеко не всегда им самим удается найти решения и доказательства, а в некоторых случаях над этим многие годы бьются их последователи и просто коллеги.
Институт Клея в 2000 году сформировал список из 7 так называемых Проблем Тысячелетия по аналогии с перечнем гипотез, составленным в 1900 году. Те задачи почти все оказались к настоящему времени решены, только одна из них перекочевала в обновленную версию. Сейчас список проблем выглядит следующим образом:
Все они относятся к различным дисциплинам внутри математики и имеют важное значение. Например, уравнения Навье-Стокса относятся к гидродинамике, а на практике могут описать поведение вещества в земной магме или пригодиться в предсказании погоды. Но все эти проблемы все еще ищут своего доказательства или опровержения. Кроме одной.
Теорема Пуанкаре
Объяснить простыми словами, в чем заключается эта проблема, довольно непросто, но попробовать можно. Представим себе сферу, к примеру, мыльный пузырь. Все точки его поверхности равноудалены от его центра, который ей не принадлежит. Но это двумерное тело, а гипотеза говорит о трехмерном. Это представить уже невозможно, но на то у нас и есть теоретическая математика. При этом, разумеется, все точки этого тела также будут удалены от центра.
История
Французский математик Анри Пуанкаре занимался самыми разными областями науки. О его достижениях может сказать, к примеру, тот факт, что совершенно независимо от Альберта Эйнштейна он выдвинул основные положения специальной теории относительности. В 1904 году он поднял проблему доказательства того, что любое трехмерное тело, обладающее некоторыми свойствами сферы, ею и является с точностью до деформации. Позднее она была расширена и обобщена, и стала частным случаем гипотезы Терстона, сформулированной в 1982 году.
Формулировка
Пуанкаре изначально оставил такое утверждение: всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере. В дальнейшем оно было расширено и обобщено. И все же на протяжении длительного времени именно изначальная задача вызывала больше всего проблем, и была решена лишь через 100 лет после ее появления.
Интерпретация и смысл
О том, что такое гомеоморфность, речь уже шла. Теперь стоит поговорить о компактности и односвязности. Первое означает лишь, что многообразие имеет ограниченные размеры, не может быть непрерывно и бесконечно растянуто.
Доказательство
Не стоит думать, что из десятков математиков, работавших по всему миру, никто не продвинулся ни на йоту, занимаясь этой проблемой. Наоборот, прогресс был, и в конце концов он привел к результату. Сам Пуанкаре не успел закончить работу, но его исследования серьезно продвинули всю топологию.
В 1982 году и для 4 было найдено доказательство, оставалось только 3. В том же году Терстон сформулирован гипотезу о геометризации, при этом теория Пуанкаре стала ее частным случаем.
На 20 лет гипотеза Пуанкаре была как будто забыта. В 2002 году российский математик Григорий Перельман представил решение в общих чертах, спустя полгода сделав некоторые дополнения. Уже позже это доказательство проверяли и доводили «до блеска» американские и китайские ученые. А сам Перельман словно потерял к проблеме весь интерес, хотя он решил более общую задачу о геометризации, для которой гипотеза Пуанкаре является лишь частным случаем.
Признание и оценки
Разумеется, это сразу стало сенсацией, ведь решение одной из Проблем Тысячелетия просто не могло оказаться незамеченным. Еще больше удивления вызывал тот факт, что Григорий Перельман отказался от всех наград и премий, сообщив, что ему и так прекрасно живется. В умах обывателей он сразу стал примером того самого полусумасшедшего гения, которого интересует только наука.
Все это вызвало много обсуждений в прессе и СМИ, что популярность математика стала его тяготить. Летом 2014 года прошла информация о том, что Перельман уехал работать в Швецию, но это оказалось лишь слухами, он все еще скромно живет в Санкт-Петербурге и почти ни с кем не общается. Среди наград, присужденных ему, были не только премия института Клея, но и престижная медаль Филдса, но он отказался от всего. Впрочем, Гамильтон, который по оценкам Перельмана сделал не меньший вклад в доказательство, тоже не был забыт. В 2009 и 2011 годах он также удостоился некоторых престижных наград и премий.
Отражение в культуре
Несмотря на то что для простых обывателей как постановка, так и решение этой проблемы представляют мало смысла, о доказательстве стало известно довольно быстро. В 2008 году по этому поводу японским режиссером Масахито Касуга был снят документальный фильм «Чары гипотезы Пуанкаре», посвященный столетним попыткам решить эту задачу.
Просто о сложном, гипотеза Пуанкаре
В переводе на общедоступный язык, это означает, что любой трёхмерный объект, например, стакан можно преобразовать в шар путём одной только деформации, то есть его не нужно будет ни разрезать, ни склеивать. Иными словами, Пуанкаре предположил, что пространство не трёхмерно, а содержит значительно большее число измерений, а Перельман спустя 100 лет математически это доказал.
Для начала заметим, что обычная сфера, которая есть поверхность обычного шара, двумерна (а сам шар — тот трёхмерен). Двумерная сфера состоит из всех точек трёхмерного пространства, равноудалённых от некоторой выделенной точки, называемой центром и сфере не принадлежащей. Трёхмерная сфера состоит из всех точек четырёхмерного пространства, равноудалённых от своего центра (сфере не принадлежащего). В отличие от двумерных сфер трёхмерные сферы недоступны нашему непосредственному наблюдению, и нам представить себе их так же трудно, как Василию Ивановичу из известного анекдота квадратный трёхчлен. Не исключено, однако, что все мы как раз в трёхмерной сфере и находимся, то есть что наша Вселенная является трёхмерной сферой. В этом состоит значение результата Перельмана для физики и астрономии. Термин “односвязное компактное трёхмерное многообразие без края” содержит указания на предполагаемые свойства нашей Вселенной. Термин “гомеоморфно” означает некую высокую степень сходства, в известном смысле неотличимость.
Формулировка в целом означает, следовательно, что если наша Вселенная обладает всеми свойствами односвязного компактного трёхмерного многообразия без края, то она — в том же самом “известном смысле” — и есть трёхмерная сфера.»
2. Имеем полое замкнутое тело, например, тарелку, стакан, куб, карандаш, дверь без ручек.
Необходимо доказать, что поверхность этого тела топологически является аналогом сферы, т.е. после проведения определённых деформаций, не вызывающих разрывов данной поверхности, поверхность принимает форму сферы и на этой поверхности действуют те же математические законы, что и на сфере, описываемые теми же функциями в топологии.
Дмитрий Кулешов Авиаконструктор, ЧГКшник, джипер., Ulan-Ude
Приведем толкование остальных терминов, фигурирующих в формулировке гипотезы:
— Полното́рие (полното́рий) — геометрическое тело, гомеоморфное произведению двумерного диска и окружности D2 * S1. Неформально, полноторие — бублик, тогда как тор — только его поверхность (пустотелая камера колеса).
— Односвязное. Оно означает, что любую непрерывную замкнутую кривую, расположенную целиком в пределах данного многообразия, можно плавно стянуть в точку, не покидая этого многообразия. Например, обычная двумерная сфера в R3 односвязна (кольцевую резинку, как угодно приложенную к поверхности яблока, можно плавной деформацией стянуть в одну точку, не отрывая резинки от яблока). С другой стороны, окружность и тор неодносвязны.
— Компактное. Многообразие компактно, если любой его гомеоморфный образ имеет ограниченные размеры. Например, открытый интервал на прямой (все точки отрезка, кроме его концов) некомпактен, так как его можно непрерывно растянуть до бесконечной прямой. А вот замкнутый отрезок (с концами) является компактным многообразием с краем: при любой непрерывной деформации концы переходят в какие-то определённые точки, и весь отрезок обязан переходить в ограниченную кривую, соединяющую эти точки.
Теорема Пуанкаре – математическая формула «Вселенной». Григорий Перельман. Часть 1 (из серии «Настоящий Человек в науке»)
Анри Пуанкаре (1854-1912), один из величайших математиков, в 1904 г. сформулировал знаменитую идею о деформированной трёхмерной сфере и в виде маленькой заметки на полях, помещённой в конце 65 страничной статьи, посвящённой совершенно другому вопросу, нацарапал несколько строчек довольно странной гипотезы со словами: «Ну этот вопрос может слишком далеко нас завести»…
Маркус Дю Сотой из Оксфордского университета считает, что теорема Пуанкаре — «это центральная проблема математики и физики, попытка понять какой формы может быть Вселенная, к ней очень трудно подобраться».
Раз в неделю Григорий Перельман ездил в Принстон, чтобы принять участие в семинаре «Института углублённых исследований». На семинаре один из математиков Гарвардского университета отвечает на вопрос Перельмана: «Теория Уильяма Тёрстона (1946-2012 гг., математик, труды в области «Трехмерной геометрии и топологии»), получившая название гипотезы геометризации описывает все возможные трёхмерные поверхности и является шагом вперёд по сравнению с гипотезой Пуанкаре. Если Вы докажете предположение Уильяма Тёрстона, то и гипотеза Пуанкаре распахнёт перед Вами все свои двери и более того её решение изменит весь топологический ландшафт современной науки».
Шесть ведущих американских университетов в марте 2003 г. приглашают Перельмана прочесть цикл лекций, разъясняющих его работу. В апреле 2003 г. Перельман совершает научное турне. Его лекции становятся выдающимся научным событием. В Принстоне послушать его приезжают Джон Болл (председатель международного математического союза), Эндрю Уайлз (математик, работы в области арифметики эллиптических кривых, доказал теорему Ферма в 1994 г.), Джон Нэш (математик, работающий в области теории игр и дифференциальной геометрии).
«Филдсовская премия (и медаль) вручается один раз в 4 года на каждом международном математическом конгрессе молодым учёным (моложе 40 лет), внёсшим заметный вклад в развитие математики. Помимо медали награждённым вручается 15 тыс. канадских долларов ($13 000)»
В исходной формулировке гипотеза Пуанкаре звучит следующим образом: «Всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере». В переводе на общедоступный язык, это означает, что любой трёхмерный объект, например, стакан можно преобразовать в шар путём одной только деформации, то есть его не нужно будет ни разрезать, ни склеивать. Иными словами, Пуанкаре предположил, что пространство не трёхмерно, а содержит значительно большее число измерений, а Перельман спустя 100 лет математически это доказал.
Выражение Григория Перельмана теоремы Пуанкаре о преобразовании материи в другое состояние, форму имеет сходство со знаниями, изложенными в книге Анастасии Новых «Сэнсэй IV»: «По факту, вся эта бесконечная для нас Вселенная занимает место в миллиарды раз меньше, чем кончик самой тонкой медицинской иглы» [3]. А также возможностью управления материальной Вселенной путём преобразований, вносимых Наблюдателем из контролирующих измерений выше шестого (с 7 по 72 включительно) (доклад «ИСКОННАЯ ФИЗИКА АЛЛАТРА» тема «Эзоосмическая решётка»). [1]
Исключительная важность гипотезы, выдвинутой около века назад математиком Пуанкаре, касается трёхмерных структур и является ключевым элементом современных исследований основ мироздания. Загадка эта, по мнению специалистов института Клэя, одна из семи принципиально важных для развития математики будущего.
Перельман, отвергая медали и премии спрашивает: «А зачем они мне? Они мне совершенно ни к чему. Каждому понятно, если доказательство правильное, то никакого другого признания уже не требуется. Пока во мне не развилась подозрительность, у меня был выбор, либо сказать вслух о дезинтеграции математического сообщества в целом, в связи с его низким моральным уровнем, либо ничего не сказать и позволить обращаться с собой, как с быдлом. Теперь же, когда я стал более чем подозрительным, я не могу оставаться быдлом и продолжать молчать, поэтому мне остаётся только уйти».
Для того чтобы заниматься современной математикой нужно иметь тотально чистый ум, без малейшей примеси, которая дезинтегрирует его, дезориентирует, подменяет ценности, и принять эту премию означает продемонстрировать слабость. Идеальный учёный занимается только наукой, не заботится больше ни о чём (власть и капитал), у него должен быть чистый ум, а для Перельмана нет большей важности, чем жить в соответствии с этим идеалом. Полезно ли для математики вся эта затея с миллионами, и нужен ли настоящему учёному такой стимул? И это желание капитала купить и подчинить себе всё в этом мире разве не оскорбительно? Или можно продать свою чистоту за миллион? Деньги, сколько бы там их ни было, эквивалентны истине Души? Ведь мы имеем дело с априорной оценкой проблем, к которым деньги просто не должны иметь отношения, разве не так?! Делать же из всего этого что-то вроде лото-миллион, или тотализатор, значит потакать дезинтеграции научного, да и человеческого сообщества в целом (см. доклад «ИСКОННАЯ ФИЗИКА АЛЛАТРА» [1] и в книге «АллатРа» [2] последние 50 страниц о пути построения созидательного общества). И денежные средства (энергия), которые бизнесмены готовы отдавать на науку, если и надо использовать, то корректно, что ли, не унижая Дух подлинного служения, как ни верти, неоценимого денежным эквивалентом: «Что такое миллион, по сравнению, с чистотой, или Величием тех сфер (об измерениях глобальной Вселенной и о Духовном мире см. книгу « АллатРа » [2] и доклад «ИСКОННАЯ ФИЗИКА АЛЛАТРА» [1]), в которые не способно проникнуть даже человеческое воображение (ум)?! Что такое миллион звёздного неба для времени?!».
Приведем толкование остальных терминов, фигурирующих в формулировке гипотезы [4]:
— Односвязное. Оно означает, что любую непрерывную замкнутую кривую, расположенную целиком в пределах данного многообразия, можно плавно стянуть в точку, не покидая этого многообразия. Например, обычная двумерная сфера в R3 односвязна (кольцевую резинку, как угодно приложенную к поверхности яблока, можно плавной деформацией стянуть в одну точку, не отрывая резинки от яблока). С другой стороны, окружность и тор неодносвязны.
— Компактное. Многообразие компактно, если любой его гомеоморфный образ имеет ограниченные размеры. Например, открытый интервал на прямой (все точки отрезка, кроме его концов) некомпактен, так как его можно непрерывно растянуть до бесконечной прямой. А вот замкнутый отрезок (с концами) является компактным многообразием с краем: при любой непрерывной деформации концы переходят в какие-то определённые точки, и весь отрезок обязан переходить в ограниченную кривую, соединяющую эти точки.