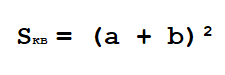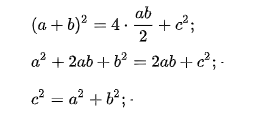в чем суть теоремы пифагора

История теоремы Пифагора. Доказательство теоремы

Тем, кто интересуется историей теоремы Пифагора, которую изучают в школьной программе, будет также любопытен такой факт, как публикация в 1940 году книги с трехсот семьюдесятью доказательствами этой, казалось бы, простой теоремы. Но она интриговала умы многих математиков и философов разных эпох. В книге рекордов Гиннеса она зафиксирована, как теорема с самым максимальным числом доказательств.

История теоремы Пифагора

Связанная с именем Пифагора, теорема была известна задолго до рождения великого философа. Так, в Египте, при строительстве сооружений, учитывалось соотношение сторон прямоугольного треугольника пять тысячелетий назад. В вавилонских текстах упоминается о все том же соотношении сторон прямоугольного треугольника за 1200 лет до рождения Пифагора.

Из жизни Пифагора

Будущий великий ученый, математик, философ родился на острове Самосе в 570 году до нашей эры. Исторические документы сохранили сведения об отце Пифагора, который был резчиком по драгоценным камням, а вот о матери сведений нет. О родившемся мальчике говорили, что это незаурядный ребенок, проявивший с детского возраста страсть к музыке и поэзии. К учителям юного Пифагора историки относят Гермодаманта и Ферекида Сиросского. Первый ввел мальчика в мир муз, а второй, будучи философом и основателем итальянской школы философии, направил взор юноши к логосу.

В 22 года от роду (548 г. до н. э.) Пифагор отправился в Навкратис для изучения языка и религии египтян. Далее его путь лежал в Мемфис, где благодаря жрецам, пройдя через их хитроумные испытания, он постиг египетскую геометрию, которая, возможно натолкнула пытливого юношу на доказательство теоремы Пифагора. История в дальнейшем припишет теореме именно это имя.

В плену царя Вавилона

По пути домой в Элладу, Пифагор попадает в плен царя Вавилона. Но нахождение в плену принесло пользу пытливому уму начинающего математика, ему было чему поучиться. Ведь в те годы математика в Вавилоне была более развитой чем в Египте. Двенадцать лет он провел за изучением математики, геометрии и магии. И, возможно, именно вавилонская геометрия причастна к доказательству соотношения сторон треугольника и истории открытия теоремы. У Пифагора было для этого достаточно полученных знаний и времени. Но, что это произошло в Вавилоне, документального подтверждения или опровержения тому нет.

В 530 г. до н.э. Пифагор бежит из плена на родину, где живет при дворе тирана Поликрата в статусе полураба. Такая жизнь Пифагора не устраивает, и он удаляется в пещеры Самоса, а затем отправляется на юг Италии, где в то время располагалась греческая колония Кротон.

Тайный монашеский орден

На базе этой колонии Пифагор организовал тайный монашеский орден, представлявший собой религиозный союз и научное общество одновременно. Это общество имело свой устав, в котором говорилось о соблюдении особого образа жизни.

Пифагор утверждал, чтобы понять Бога, человек должен познать такие науки как алгебра и геометрия, знать астрономию и понимать музыку. Исследовательская работа сводилась к познанию мистической стороны чисел и философии. Следует отметить, что проповедованные в то время Пифагором принципы, имеют смысл в подражании и в настоящее время.

Многие из открытий, которые делали ученики Пифагора, приписывались ему. Тем не менее, если говорить кратко, история создания теоремы Пифагора древними историками и биографами того времени, связывается непосредственно с именем этого философа, мыслителя и математика.

Учение Пифагора

Возможно, на мысль о связи теоремы с именем Пифагора натолкнуло историков высказывание великого грека, что в пресловутом треугольнике с его катетами и гипотенузой зашифрованы все явления нашей жизни. А этот треугольник является «ключом» к решению всех возникающих проблем. Великий философ говорил, что следует узреть треугольник, тогда можно считать, что задача на две трети решена.

О своем учении Пифагор рассказывал только своим ученикам устно, не делая никаких записей, держа его в тайне. К великому сожалению, учение величайшего философа не сохранилось до наших дней. Что-то из него просочилось, но нельзя сказать сколько истинного, а сколько ложного в том, что стало известно. Даже с историей теоремы Пифагора не все бесспорно. Историки математики сомневаются в авторстве Пифагора, по их мнению теоремой пользовались за много веков до его рождения.

Теорема Пифагора

Может показаться странным, но исторических фактов доказательства теоремы самим Пифагором нет — ни в архивах, ни в каких-либо других источниках. В современной версии считается, что оно принадлежит не кому иному, как самому Евклиду.

Есть доказательства одного из крупнейших историков математики Морица Кантора, обнаружившего на папирусе, хранящемся в Берлинском музее, записанное египтянами примерно в 2300 году до н. э. равенство, которое гласило: 3² + 4² = 5².

Кратко из истории теоремы Пифагора

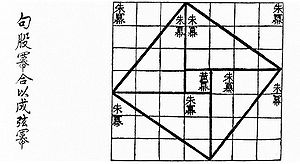
Формулировка теоремы из евклидовых «Начал», в переводе звучит также как и в современной интерпретации. Нового в ее прочтении нет: квадрат стороны противолежащей прямому углу, равен сумме квадратов сторон, прилегающих к прямому углу. О том, что теоремой пользовались древние цивилизации Индии и Китая подтверждает трактат «Чжоу — би суань цзинь». Он содержит сведения об египетском треугольнике, в котором описано соотношение сторон как 3:4:5.

Не менее интересна еще одна китайская математическая книга «Чу-пей», в которой также упоминается о пифагоровом треугольнике с пояснением и рисунками, совпадающими с чертежами индусской геометрии Басхары. О самом треугольнике в книге написано, что если прямой угол можно разложить на составные части, тогда линия, которая соединяет концы сторон, будет равна пяти, если основание равно трем, а высота равна четырем.

Индийский трактат «Сульва сутра», относящийся примерно к VII-V векам до н. э., рассказывает о построении прямого угла при помощи египетского треугольника.

Доказательство теоремы

В средние века ученики считали доказательство теоремы слишком трудным делом. Слабые ученики заучивали теоремы наизусть, без понимания смысла доказательства. В связи с этим они получили прозвище «ослы», потому что теорема Пифагора была для них непреодолимым препятствием, как для осла мост. В средние века ученики придумали шутливый стих на предмет этой теоремы.

Если начать доказательство теоремы с рассмотрения площади прямоугольников, построенных на сторонах треугольника, можно определить площадь всей фигуры. Она будет равна площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырех треугольников и внутреннего квадрата.

(a + b) 2 = 4 x ab/2 + c 2 ;

То ли еще будет. Безграничный простор для открытия и создания новых технологий ждет пытливые умы.

Источник

Теорема Пифагора: история, формулы и доказательства

Теорема Пифагора – одна из самых известных геометрических теорем, которая устанавливает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Большинство ученых считают, что теорема Пифагора была доказана древнегреческим математиком и философом Пифагором (или Питагором). Однако есть версия, что теорему знали и до его рождения. Доказательством этого является то, что в Древнем Египте знали, что треугольник, у которого стороны имеют 3 см, 4 см и 5 см, является прямоугольным. А о других теоремах можно узнать в учебнике по геометрии за 8 класс А.Г. Мерзляка.

Еще в детстве Пифагор отличился интересом к точным наукам. Впоследствии он переехал жить на остров Лесбос, где познакомился с Фалесом Милетским – древнегреческим философом и математиком, который доказал теоремы о трех точках на окружности и пропорциональных отрезках. За время, когда Пифагор учился в Милетской школе, он изучал астрологию, медицину, прогнозы затмений и другие важные в то время науки. Лекции Фалеса и его ученика Анаксимандра сыграли важную роль для Пифагора.

После обучения в Египте, плена в Вавилоне, в 60 лет Пифагор решает вернуться домой, чтобы поделиться своими знаниями с народом. Впоследствии он открыл собственную школу, в которой геометрия впервые выступает как самостоятельная наука.

О том, что квадрат гипотенузы равен сумме квадратов катетов, знали задолго до рождения Пифагора. Но именно он считается первым ученым, который доказал соотношение сторон треугольника.

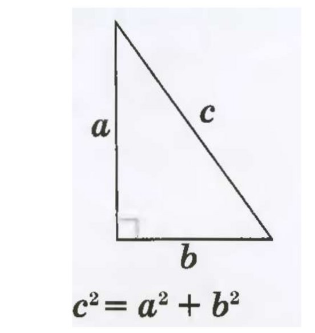
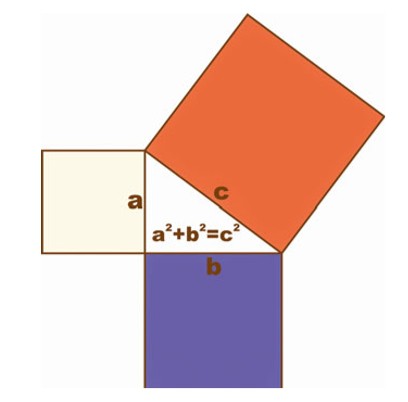
В теореме Пифагора говорится, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Пусть ВС = а; АС = b; АВ = с.

Тогда имеем такую формулу, которая применяется при нахождении неизвестной стороны в прямоугольном треугольнике, когда две другие – известны:

Когда мы определили квадрат гипотенузы, нужно найти квадратный корень. Такую же формулу мы можем применить к неизвестному катету:

А больше рисунков и формул можно увидеть в онлайн уроке за 8 класс по геометрии на тему «Метрические соотношения в прямоугольном треугольнике. Теорема Пифагора».

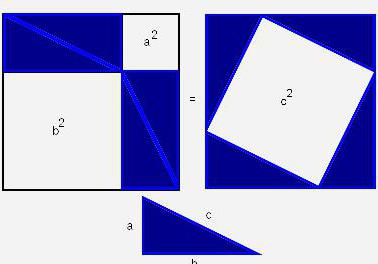
Самый популярный и самый простой метод доказательства теоремы связан с площадями фигуры.

Нужно расположить одинаковые прямоугольные треугольники так, чтобы внутри образовался квадрат. Каждая сторона внешнего квадрата должна состоять из суммы катетов прямоугольного треугольника a + b.

Площадь этого квадрата можно будет найти благодаря формуле:

Внутренний четырехугольник можно считать квадратом, ведь, если добавить два острые углы прямоугольного треугольника, то получится 90°. Следует считать, что площадь внешнего квадрата состоит из площади внутреннего квадрата и четырех площадей одинаковых прямоугольных треугольников. Итак, в заключении:

Итак, теорема Пифагора доказана.

2. Доказательство Евклида

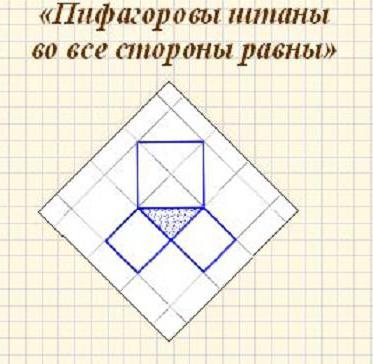
Доказательство Евклида также называется «Пифагоровы штаны». Ее так назвали, потому что сумма площади квадратов, образованных с использованием катетов прямоугольного треугольника равна площади квадрата, который построен на гипотенузе этого же треугольника. Квадраты напоминали ученикам мужские штаны.

На примере приведенных картинок ниже можно увидеть, как оригинально передали суть доказательства Евклида.

В вашем учебнике не было таких доказательств? Вы можете найти другой в разделе «Учебники по геометрии за 8 класс».

Пример задачи на применение теоремы Пифагора

Условия задачи. В треугольнике ABC дано: ∠C = 90 °, BC = 20 см, AC = 15 см. Найти сторону AB.

Решение. Поскольку в треугольнике АВС ∠С = 90°, следовательно, по теореме Пифагора имеем:

АВ² = BС² + АС²; AВ² = 20² + 15², AВ² = 625, AB = √625| AB = 25 см.

Если вам нужно решить задачу с помощью теоремы Пифагора, а вы сомневаетесь в конечном ответе, тогда можете проверить свои знания благодаря разделу «ГДЗ и решебники по геометрии за 8 класс».

А если вы хотите крепче закрепить знания по другим темам по геометрии, то можете просматривать видео в разделе «Онлайн уроки за 8 класс по геометрии». Узнайте больше о перпендикуляре и наклонной, сумме углов выпуклого треугольника, площадь квадрата и прямоугольника, решение задач методом площадей и тому подобное.

Источник

Теорема Пифагора

Теорема Пифагора — квадрат гипотенузы равен сумме квадратов катетов (в прямоугольном треугольнике); формула: c² = a² + b².

Доказательство

Доказательство теоремы Пифагора, используя алгебру

Нужно доказать, что c² = a² + b²:

Это квадрат, в котором есть 4 одинаковых треугольника abc:

Что и требовалось доказать.

«Пифагоровы штаны на все стороны равны»

Это шуточная фраза, которая именует ещё одно доказательство теоремы Пифагора

На этой фигуре c — гипотенуза, a и b — катеты.

Проведём перпендикулярную линию к гипотенузе (c):

Таким образом появились два новых прямоугольных треугольника (A и B) внутри большого (исходный треугольник С).

Что и требовалось доказать.

Примеры

Задача 1

На рисунке видно, что длина одной стороны прямоугольного треугольника составляет 3 см, длина другой — 4 см. Найдите длину гипотенузы.

Подставить известные значения

Ответ: длина гипотенузы равна 5.

Задача 2

Длина одной стороны прямоугольного треугольника составляет 12 см, длина гипотенузы 13 см. Найдите длину другой стороны треугольника.

Подставить известные значения

Ответ: длина другой стороны треугольника равна 5.

Следствия из теоремы Пифагора

Это основные следствия теоремы:

Кто придумал теорему Пифагора

Концепция теоремы Пифагора была известна ещё в древнем Египте и Вавилоне (около 1900 г. до н. э.). Связь между катетами и гипотенузой в прямоугольном треугольнике была изображена на вавилонской глиняной табличке (которой около 4000 лет). Однако это знание стало широко использоваться лишь после того, как сам Пифагор заявил о нём (он жил в 6 веке до н. э.).

Узнайте также, что такое Теорема Виета и Аксиома.

Источник

Пифагор и его теорема

Пифагору (570—490 гг. до н. э.) принадлежит доказательство знаменитой теоремы о том, что сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.

Пифагор родился на острове Самос. Считается, что он побывал и в Египте, и в Вавилоне, но в конце концов поселился в Кротоне — греческой колонии на юге Италии. Там он основал пифагорейский религиозно-мистический союз. Его члены были вегетарианцами, проповедовали аскетизм и считали основой всего число. Среди последователей Пифагора были знатные люди, которые практически захватили власть в Кротоне. Это вызвало недовольство, наука смешалась с политикой, и Пифагору пришлось покинуть город. А после его смерти пифагорейский союз был разгромлен.

Теорема Пифагора

Теорема Пифагора широко применяется на практике, например в мобильной связи. Нужно определить высоту АВ антенны (вышки), чтобы сигнал от неё передавался на расстояние 30 км, до точки С.

ВС — касательная к окружности Земли, следовательно, она перпендикулярна радиусу Земли ОС. Имеется прямоугольный треугольник ВСО, его гипотенуза — ОА + АВ (высота антенны + радиус Земли 6371 км). Известна длина его катетов:

ВС — 30 км, СО — 6371 км, вычисляем длину гипотенузы:

302 + 63712 = 900 + 40589641 = 405905541 (квадрат длины гипотенузы).

Длина гипотенузы: V40590541 = 6371,070632162227 км.

Высота антенны: 6371,070632162227 — 6371 = 0,070632162227 км = 70 м.

Источник

Теорема Пифагора

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

Содержание

История

В древнекитайской книге Чу-пей (англ.) (кит. 周髀算經 ) говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.

Мориц Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам ещё около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора, гарпедонапты, или «натягиватели верёвок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Очень легко можно воспроизвести их способ построения. Возьмём верёвку длиною в 12 м и привяжем к ней по цветной полоске на расстоянии 3 м от одного конца и 4 метра от другого. Прямой угол окажется заключённым между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становится излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, — например, рисунки, изображающие столярную мастерскую.

Приблизительно в 400 г. до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Приблизительно в 300 г. до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора. [7]

Формулировки

Изначально теорема была сформулирована следующим образом:

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

То есть, обозначив длину гипотенузы треугольника через , а длины катетов через и :

Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.

Обратная теорема Пифагора:

Для всякой тройки положительных чисел , и , такой, что , существует прямоугольный треугольник с катетами и и гипотенузой .

Доказательства

Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений).

Через подобные треугольники

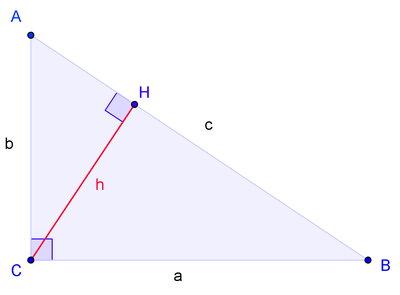
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.

Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения

, что и требовалось доказать

Доказательства методом площадей

Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость

Что и требовалось доказать.

Доказательство Евклида

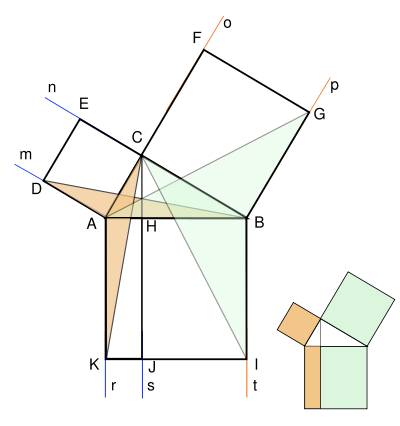
Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.

Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах.

Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.

Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно: треугольники равны по двум сторонам и углу между ними. Именно — AB=AK, AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).

Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.

Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше.

Данное доказательство также получило название «Пифагоровы штаны».

Доказательство Леонардо да Винчи

Главные элементы доказательства — симметрия и движение.

Рассмотрим чертёж, как видно из симметрии, отрезок рассекает квадрат на две одинаковые части (так как треугольники и равны по построению).

Пользуясь поворотом на 90 градусов против часовой стрелки вокруг точки , мы усматриваем равенство заштрихованных фигур и .

Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей маленьких квадратов (построенных на катетах) и площади исходного треугольника. С другой стороны, она равна половине площади большого квадрата (построенного на гипотенузе) плюс площадь исходного треугольника. Таким образом, половина суммы площадей маленьких квадратов равна половине площади большого квадрата, а следовательно сумма площадей квадратов, построенных на катетах равна площади квадрата, построенного на гипотенузе.

Доказательство методом бесконечно малых

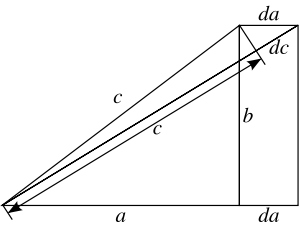
Следующее доказательство при помощи дифференциальных уравнений часто приписывают известному английскому математику Харди, жившему в первой половине XX века.

Рассматривая чертёж, показанный на рисунке, и наблюдая изменение стороны a, мы можем записать следующее соотношение для бесконечно малых приращений сторон с и a (используя подобие треугольников):

Пользуясь методом разделения переменных, находим

Более общее выражение для изменения гипотенузы в случае приращений обоих катетов

Интегрируя данное уравнение и используя начальные условия, получаем

Таким образом, мы приходим к желаемому ответу

Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.

Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения (в данном случае катет ). Тогда для константы интегрирования получим

Вариации и обобщения

Подобные геометрические фигуры на трех сторонах

Обобщение теоремы Пифагора сделал Евклид в своей работе Начала, расширив площади квадратов на сторонах до площадей подобных геометрических фигур [9] :

Если построить подобные геометрические фигуры (см. Евклидова геометрия) на сторонах прямоугольного треугольника, тогда сумма двух меньших фигур будет равняться площади большей фигуры.

Главная идея этого обобщения заключается в том, что площадь подобной геометрической фигуры пропорциональна квадрату любого своего линейного размера и в частности квадрату длины любой стороны. Следовательно, для подобных фигур с площадями A, B и C построенных на сторонах с длиной a, b и c, имеем:

Теорема косинусов

Теорема Пифагора — это частный случай более общей теоремы косинусов, которая связывает длины сторон в произвольном треугольнике: [10]

где θ — угол между сторонами a и b.

Если θ равен 90 градусов, тогда cosθ = 0 и формула упрощается до обычной теоремы Пифагора.

Произвольный треугольник

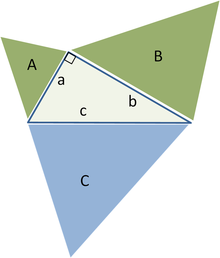
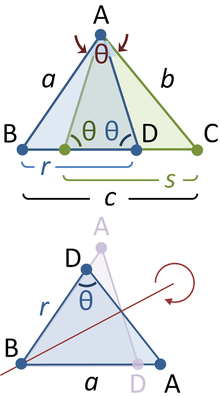
В любой выбранный угол произвольного треугольника со сторонами a, b, c впишем равнобедренный треугольник таким образом, чтобы равные углы при его основании θ равнялись выбранному углу. Предположим, что выбранный угол θ расположен напротив стороны, обозначенной c. В результате мы получили треугольник ABD с углом θ, что расположен напротив стороны a и стороны r. Второй треугольник образуется углом θ, что расположен напротив стороны b и стороны с длиной s, как показано на рисунке. Сабит Ибн Курра [12] утверждал, что стороны в этих трех треугольниках связаны следующим образом: [13] [14]

Когда угол θ приближается к π/2, основание равнобедренного треугольника уменьшается, и две стороны r и s перекрывают друг друга все меньше и меньше. Когда θ = π/2, ADB превращается в прямоугольный треугольник, r + s = c и получаем начальную теорему Пифагора.

Рассмотрим один из доводов. Треугольник ABC имеет такие же углы, как и треугольник ABD, но в обратном порядке. (Два треугольника имеют общий угол при вершине B, оба имеют угол θ и также имеют одинаковый третий угол, по сумме углов треугольника) Соответственно, ABC — подобен отражению ABD треугольника DBA, как показано на нижнем рисунке. Запишем соотношение между противоположными сторонами и прилегающими к углу θ,

Так же отражение другого треугольника,

Перемножим дроби и добавим эти два соотношения:

что и требовалось доказать.

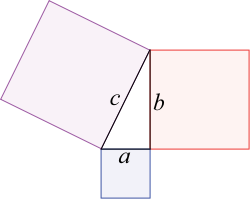
Обобщение для произвольных треугольников через параллелограммы

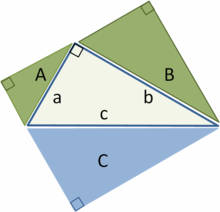
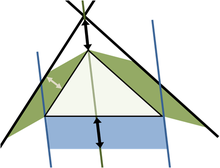
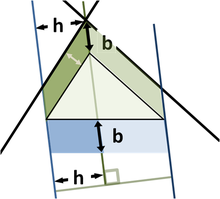
Сделаем дальнейшее обобщение для непрямоугольных треугольников, используя параллелограммы на трех сторонах вместо квадратов. [15] (квадраты — частный случай.) Верхний рисунок демонстрирует, что для остроугольного треугольника площадь параллелограмма на длинной стороне равна сумме параллелограммов на двух других сторонах, при условии что параллелограмм на длинной стороне построен, как изображено на рисунке (размеры, отмеченные стрелками, одинаковые и определяют стороны нижнего параллелограмма). Эта замена квадратов параллелограммами имеет четкое сходство с начальной теоремой Пифагора, считается, что её сформулировал Папп Александрийский в 4 г. н. э. [15]

Нижний рисунок показывает ход доказательства. Посмотрим на левую сторону треугольника. Левый зеленый параллелограмм имеет такую же площадь, как левая часть синего параллелограмма, потому что они имеют такое же основание b и высоту h. Кроме того, левый зеленый параллелограмм имеет такую же площадь, как левый зеленый параллелограмм на верхнем рисунке, потому что они имеют общее основание (верхняя левая сторона треугольника) и общую высоту, перпендикулярную к этой стороне треугольника. Аналогично рассуждая для правой стороны треугольника докажем, что нижний параллелограмм имеет такую же площадь, как у двух зеленых параллелограммов.

Комплексные числа

Теорему Пифагора используют, чтобы найти расстояние между двумя точками в декартовой координатной системе, и эта теорема справедлива для всех истинных координат: расстояние s между двумя точками (a, b) и (c, d) равно

Тем не менее, для операций с векторами с комплексными координатами необходимо провести определенное усовершенствование формулы Пифагора. Расстояние между точками с комплексными числами (a, b) и (c, d); a, b, c, и d все комплексные, сформулируем используя абсолютные величины. Расстояние s основано на векторной разнице (a − c, b − d) в следующем виде: [16] пусть разница a − c = p + i q, где p — действительная часть разницы, q — мнимая часть, и i = √(−1). Аналогично, пусть b − d = r + is. Тогда:

Модуль определен следующим образом:

Стереометрия

Значительным обобщением теоремы Пифагора для трехмерного пространства является теорема де Гуа, названная в честь Ж.-П. де Гуа: если тетраэдр имеет прямой угол (как в кубе), тогда квадрат площади грани, лежащей напротив прямого угла, равен сумме квадратов площадей других трех граней. Этот вывод может быть обобщен как «n-мерная теорема Пифагора»: [18]

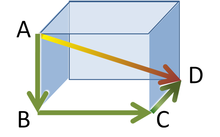
Другое обобщение: Теорема Пифагора может быть применена для стереометрии в следующем виде. Рассмотрим прямоугольный параллелепипед, как показано на рисунке. Найдем длину диагонали BD по теореме Пифагора:

где три стороны образуют прямоугольный треугольник. Используем горизонтальную диагональ BD и вертикальное ребро AB, чтобы найти длину диагонали AD, для этого снова используем теорему Пифагора:

или, если все записать одним уравнением:

Этот результат — это трехмерное выражение для определения величины вектора v (диагональ AD), выраженного через его перпендикулярные составляющие <v_k> (три взаимно перпендикулярные стороны):

Это уравнение можно рассматривать как обобщение теоремы Пифагора для многомерного пространства. Однако, результат на самом деле есть не что иное, как неоднократное применение теоремы Пифагора к последовательности прямоугольных треугольников в последовательно перпендикулярных плоскостях.

Векторное пространство

В случае ортогональной системы векторов имеет место равенство, которое тоже называют теоремой Пифагора:

Если — это проекции вектора на координатные оси, то эта формула совпадает с расстоянием Евклида — и означает, что длина вектора равна корню квадратному суммы квадратов его компонентов.

Аналог этого равенства в случае бесконечной системы векторов имеет название равенства Парсеваля.

Неевклидова геометрия

Рассмотрим здесь два случая неевклидовой геометрии — сферическая и гиперболическая геометрия; в обоих случаях, как и для евклидова пространства для прямоугольных треугольников, результат, который заменяет теорему Пифагора, следует из теоремы косинусов.

Однако, теорема Пифагора остается справедливой для гиперболической и эллиптической геометрии, если требование о прямоугольности треугольника заменить условием, что сумма двух углов треугольника должна равняться третьему, скажем A+B = C. Тогда соотношение между сторонами выглядит так: сумма площадей кругов с диаметрами a и b равна площади круга с диаметром c. [22]

Сферическая геометрия

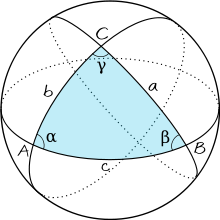
Для любого прямоугольного треугольника на сфере радиусом R (например, если угол γ в треугольнике прямой) со сторонами a, b, c соотношение между сторонами будет иметь такой вид: [23]

Это равенство может быть выведено как особый случай сферической теоремы косинусов, которое справедливо для всех сферических треугольников:

Применяя ряд Тейлора в функции косинуса cos x ≈ 1 − x 2 /2 можно показать, что если радиус R приближается к бесконечности, а аргументы a/R, b/R и c/R приближаются к нулю, сферическое соотношение между сторонами в прямоугольном треугольнике приближается к теореме Пифагора. Подставим приближенные значения для каждого косинуса:

Перемножим выражения в скобках, получим теорему Пифагора для больших радиусов R:

где «higher order terms» — слагаемые высшего порядка, которыми можно пренебречь при больших значениях R.

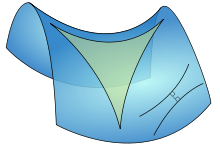
Гиперболическая геометрия

Для прямоугольного треугольника в гиперболической геометрии со сторонами a, b, c, если сторона c расположена напротив прямого угла, соотношение между сторонами будет такое [24]

где cosh — это гиперболический косинус. Эта формула является частным случаем гиперболической теоремы косинусов, которая справедлива для всех треугольников: [25]

где γ — это угол, вершина которого противоположна стороне c.

Дифференциальная геометрия

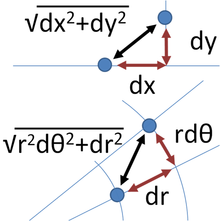
В трехмерном пространстве для двух точек, удаленных друг от друга на бесконечно малое расстояние, запишем теорему Пифагора:

где ds — это расстояние между точками, а (dx, dy, dz) — компоненты вектора, соединяющие эти две точки. Такое пространство называется евклидовым. Однако, обобщение этого выражения пригодно для общих координат (не только декартовых) и общих пространств (не только евклидовых) и имеет вид: [26]

где g_ij называется метрическим тензором. Он может быть функцией позиции. Такие криволинейные пространства включают Риманову геометрию как общий пример. Это формулировка также подходит для Евклидова пространства при применении криволинейных координат. Например, для полярных координат:

Векторное произведение

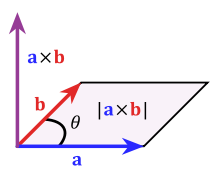
Теорема Пифагора связывает два выражения величины векторного произведения. Один из подходов к определению векторного произведения требует, чтобы он удовлетворял уравнению: [27]

в этой формуле используется скалярное произведение. Правая сторона уравнения называется детерминант Грамма для a и b, что равно площади параллелограмма, образованного этими двумя векторами. Исходя из этого требования, а также требования о перпендикулярности векторного произведения к его составляющим a и b следует, что, за исключением тривиальных случаев из 0- и 1-мерного пространства, векторное произведение определено только в трех и семи измерениях. [28] Используем определение угла в n-мерном пространстве: [29]

это свойство векторного произведения дает его величину в таком виде:

Через фундаментальное тригонометрическое тождество Пифагора [30] получаем другую форму записи его величины:

Альтернативный подход к определению векторного произведения использует выражение для его величины. Тогда, рассуждая в обратном порядке, получаем связь со скалярным произведением:

Источник