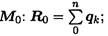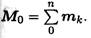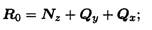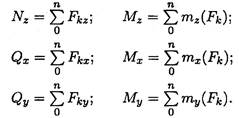в чем суть метода сечений
Метод сечений



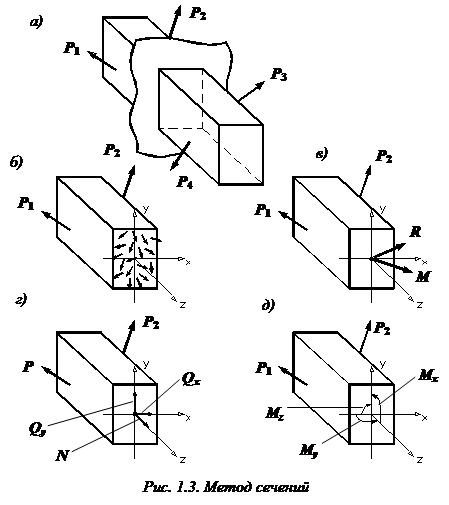
Метод сечений заключается в мысленном рассечении тела плоскостью и рассмотрении равновесия любой из отсеченных частей.
Если все тело находится в равновесии, то и каждая его часть находится в равновесии под действием внешних и внутренних сил. Внутренние силы определяются из уравнений равновесия, составленных для рассматриваемой части тела.
Рассекаем тело поперек плоскостью (рис. 19.1). Рассматриваем правую часть. На нее действуют внешние силыF4; F5; F6 и внутренние силы упругости qк, распределенные по сечению. Систему распределенных сил можно заменить главным вектором Ro, помещенным в центр тяжести сечения, и суммарным моментом сил.
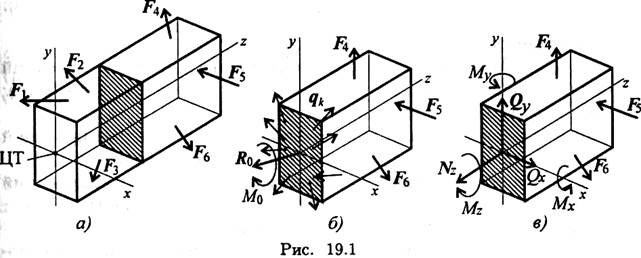 |
Разложив главный вектор Ro по осям, получим три составляющие:
гдеNz — продольная сила;
Qx — поперечная сила по оси х;
Qy — поперечная сила по оси у.
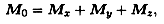 |
Главный момент тоже принято представлять в виде моментов пар сил в трех плоскостях проекции:
Полученные составляющие сил упругости носят название внутренних силовых факторов. Каждый из внутренних силовых факторов вызывает определенную деформацию детали. Внутренние силовые факторы уравновешивают приложенные к этому элементу детали внешние силы. Используя шесть уравнений равновесия, можно получить величину внутренних силовых факторов:
Из приведенных уравнений следует, что:
Nz — продольная сила, равная алгебраической сумме проекций на ось Oz внешних сил, действующих на отсеченную часть бруса; вызывает растяжение или сжатие;
Qx — поперечная сила, равная алгебраической сумме проекций на ось Ох внешних сил, действующих на отсеченную часть;
Qy — поперечная сила, равная алгебраической сумме проекций на ось Оу внешних сил, действующих на отсеченную часть;
силы Qx и Qy вызывают сдвиг сечения;
Mz — крутящийся момент, равный алгебраической сумме моментов внешних сил относительно продольной оси Oz-, вызывает скручивание бруса;
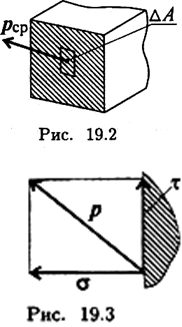
Му — изгибающий момент, равный алгебраической сумме моментов внешних сил относительно оси Оу.
Моменты Мх и Му вызывают изгиб бруса в соответствующей плоскости.
Метод сечений



Силы являются мерилом механического взаимодействия тел. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на нее заменяется силами, которые называются внешними. Внешние силы, действующие на тело, можно разделить на активные (независимые) и реактивные. Реактивные усилия возникают в связях, наложенных на тело, и определяются действующими на тело активными усилиями.
По способу приложения внешние силы делятся на объемные и поверхностные.
Объемные силы распределены по всему объему рассматриваемого тела и приложены к каждой его частице. В частности, к объемным силам относятся собственный вес сооружения, магнитное притяжение или силы инерции. Единицей измерения объемных
Взаимодействие между частями рассматриваемого тела характеризуется внутренними силами, которые возникают внутри тела под действием внешних нагрузок и определяются силами межмолекулярного воздействия.
Величины внутренних усилий определяются с применением метода сечений, суть которого заключается в следующем. Если при действии внешних сил тело находится в состоянии равновесия, то любая отсеченная часть тела вместе с приходящимися на нее внешними и внутренними усилиями также находится в равновесии, следовательно, к ней применимы уравнения равновесия.
Рассмотрим тело, имеющее форму бруса (рис. 1.2, а).
 |
Если рассечь брус сечением А на две части и правую отбросить, то, т.к. связи между частями тела устранены, необходимо действие правой (отброшенной) части на левую заменить некоей системой внутренних сил (PА ), действующей в сечении А (рис. 1.2, б).
Обозначая через Pлев и Рправ суммы внешних сил, приложенных соответственно, к левой и правой частям бруса (относительно сечения А), и учитывая, что
для отсеченных частей бруса получим следующие очевидные соотношения:
Последние соотношения показывают, что равнодействующая внутренних сил РА в сечении А может определяться с равным успехом из условий равновесия либо левой, либо правой частей рассеченного тела. В этом суть метода сечений.
Внутренние усилия должны быть так распределены по сечению, чтобы деформированные поверхности сечения А при совмещении правой и левой частей тела в точности совпадали. Это требование в механике твердого деформируемого тела носит название условия неразрывности деформаций.
При известных внешних силах все шесть внутренних силовых
факторов в сечении определяются из шести уравнений равновесия,
которые могут быть составлены для отсеченной части.
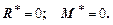
Последние два векторные уравнения равновесия дают шесть скалярных уравнений в проекциях на декартовых осях координат:
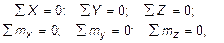
которые в общем случае составляют замкнутую систему алгебраических уравнений относительно шести неизвестных внутренних усилий: Qx, Qy, Nz, Mx, My, Mz.
Следовательно, если полная система внешних сил известна, то по методу сечений, всегда можно определить все внутренние усилия действующих в произвольно взятом сечении тела. Данное положение является основополагающим обстоятельством в механике твердого деформируемого тела.
 |
Сопротивления, при которых в поперечном сечении бруса действует одно внутреннее усилие, условно называются простыми. При одновременном действии в сечении бруса двух и более усилий сопротивление бруса называется сложным.
В заключение заметим, что при выполнении практических расчетов, для наглядности, как правило, определяются графики функций внутренних силовых факторов относительно координатной оси, направленной вдоль продольной оси стержня. Графики изменения внутренних усилий вдоль продольной оси стержня называются эпюрами.
Метод сечений. Силовые факторы в методе сечений
Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.
Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).
Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.
Этапы метода сечений
Разрежем стержень, находящийся в равновесии под действием некоторой системы сил 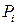
Отбросим одну из частей стержня и рассмотрим оставленную часть.
Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые при деформации тела возникли между этими частицами. Иными словами, заменим действие отброшенной части внутренними силами (рис. 1.3, б).
Внутренние силы в методе сечений
Разложим главный вектор и главный момент на составляющие по осям x, y (главные центральные оси) и z.
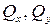
момент относительно оси z (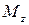
моменты относительно осей x, y (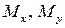
Запишем для оставленной части тела уравнения равновесия ( уравновесим ):
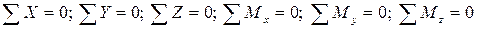
Из уравнений определяются внутренние усилия, возникающие в рассматриваемом поперечном сечении стержня.
Вычисление продольной и поперечных сил, крутящего и изгибающих моментов
продольная сила N равна сумме проекций всех сил (активных и реактивных), действующих на любую из частей рассеченного стержня, на ось z;
поперечные силы 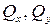
крутящий момент 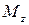
изгибающие моменты 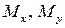
Методы построения сечений многогранников
Разделы: Математика
Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.
построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.
Первые два метода являются разновидностями Аксиоматического метода построения сечений.
Рассмотрим подробнее учебники Л.С, Атанасяна и Погорелова А.В.
В учебнике Л.С. Атанасяна на тему “Построение сечений многогранников” выделено два часа. В 10 классе в теме “Параллельность прямых и плоскостей” после изучения тетраэдра и параллелепипеда отводится один час на изложение параграфа “Задачи на построение сечений”. Рассматриваются сечения тетраэдра и параллелепипеда. И тема “Параллельность прямых и плоскостей” завершается решением задач на одном или двух часах (всего задач на построение сечений в учебнике восемь).
В учебнике Погорелова А.В. на построение сечений отводится около трех часов в главе “Многогранники”: один – на изучение темы “Изображение призмы и построение ее сечений”, второй – на изучение темы “Построение пирамиды и ее плоских сечений” и третий – на решение задач. В списке задач, приведенных после темы, задач на сечение насчитывается всего около десяти.
Мы предлагаем систему уроков по теме “Построение сечений многогранников” для учебника Погорелова А.В.
СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.
(система уроков и факультативных занятий по теме “Построение сечений многогранников”)
Тема урока: “Построение сечений многогранников”.
Цель урока: ознакомление с методами построений сечений многогранников.
Метод сечений
Содержание:
Метод сечений (см. рис. 2) состоит в том, что брус, находящийся в равновесии под действием системы внешних сил, мысленно рассекают на две части (рис. 2, а), и рассматривают равновесие одной из них, заменяя действие отброшенной части бруса системой внутренних сил, распределенных по сечению (рис. 2, б).
Заметим, что внутренние силы для бруса в целом, становятся внешними для одной из его частей. Причем во всех случаях внутренние усилия уравновешивают внешние силы, действующие на отсеченную часть бруса.
В соответствии с правилом параллельного переноса сил статики приведем все распределенные внутренние силы к центру тяжести сечения. В результате получим их главный вектор 

Для наглядного представления характера изменения внутренних силовых факторов вдоль оси бруса строят их графики, называемые эпюрами.
Эпюры позволяют определить наиболее нагруженные участки бруса и установить опасные сечения.
Внутри любого материала имеются внутренние межатомные силы, наличие которых определяет способность тела воспринимать действующие на него внешние силы, сопротивляться разрушению, изменению формы и размеров. Приложение к телу внешней нагрузки вызывает изменение (увеличение или уменьшение) внутренних сил, т. е. появление дополнительных внутренних сил.
В сопротивлении материалов изучаются дополнительные внутренние силы. Поэтому под внутренними силами (или внутренними усилиями) в сопротивлении материалов понимают силы взаимодействия между отдельными элементами сооружения или между отдельными частями элемента, возникающие под действием внешних сил. Это понятие равносильно допущению об отсутствии в теле внутренних сил до приложения к нему внешних нагрузок. Поэтому иногда считают, что в сопротивлении материалов принимается гипотеза о ненапряженном начальном состоянии тела.
Рассмотрим элемент конструкции, на который действует система внешних сил, находящихся в равновесии (рис. 4.1,а). Напоминаем, что в число внешних сил входят как заданные активные силы, так и реакции связей. Мысленно рассечем элемент плоскостью 
Этим силам (на основании известного закона механики: действие равно противодействию) равны по величине и противоположны по направлению внутренние силы воздействия левой части элемента на правую.
В общем случае пространственной задачи взаимодействие между левой и правой частями элемента можно представить некоторой силой 



Возможно вам будут полезны данные страницы:
Сила 

Определение внутренних сил, возникающих в брусе, обычно производится для сечений, перпендикулярных к его продольной оси, т. е. для поперечных сечений бруса. Точка 
Главный вектор 





Каждому из внутренних усилий 




Внутренние усилия 





Таким образом, взаимодействие любых двух частей конструкции характеризуется тремя составляющими 

Рассмотрим общий прием определения внутренних усилий, называемый методом сечений.
Рассечем стержень (рис. 6.1, а) плоскостью 


Правая часть стержня (рис. 6.1,в) находится в равновесии; значит, внешние силы 


Таким образом, проекция на какую-либо ось внутренних усилий в сечении, действующих со стороны левой части стержня на правую, равна проекции на эту ось всех внешних сил, приложенных к левой части.
Аналогично, момент относительно какой-либо оси внутренних усилий в сечении, действующих со стороны левой части стержня на правую, равен моменту всех внешних сил, приложенных к левой части относительно этой оси.
Из шести внутренних усилий, действующих в поперечном сечении стержня, проекции пяти усилий на каждую из осей 



Определим, например, величину продольной силы 







оси 

Внутренние силы, действующие в сечении со стороны левой части на правую, можно определить по внешним силам, приложенным не к левой, а к правой части. В этом случае полученные направления проекций внешних сил на выбранные оси и моментов относительно этих осей необходимо изменять на противоположные.
Внутренние усилия в каком-либо сечении обычно определяют по внешним силам, приложенным к той части конструкции (расположенной по одну сторону от рассматриваемого сечения), на которую действует меньше сил.
В теоретической механике, в разделе статики, широко применяется замена системы сил их равнодействующей и перенос силы по линии ее действия. В сопротивлении материалов это не всегда возможно, так как может приводить к неправильным результатам. Например, совершенно очевидно, что при определении внутренних сил в сечении 

На странице -> решение задач по сопротивлению материалов (сопромат) собраны решения задач и заданий с решёнными примерами по всем темам сопротивления материалов.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.