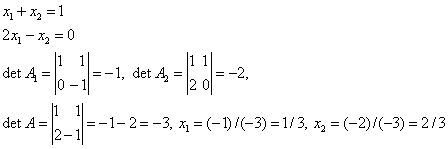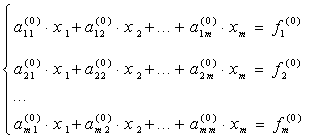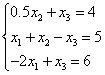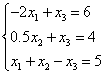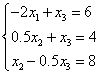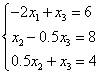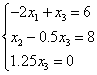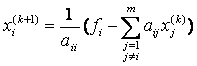в чем суть итерационного метода решения систем линейных алгебраических уравнений

Итерационные методы решения СЛАУ

Вы будете перенаправлены на Автор24

Для решения систем линейных уравнений используется два основных метода решений, прямые методы, также называемые точными и итерационные методы, при использовании которых ответ в любом случае будет приближённым.

Особенность прямых методов состоит в том, что вычисления в них всегда проводятся точно, например, с использованием целых чисел, но при этом эти методы трудно применимы для вычисления решений для больших систем. К прямому методу относится, например, метод Крамера.

Ниже подробно рассмотрены итерационные методы решения СЛАУ.

Сущность итерационных методов решения систем линейных уравнений

Как уже отмечалось выше, итерационные методы в принципе являются приближёнными. Их сущность состоит в том, что сначала записывается некоторая последовательность столбцов матрицы, после чего производится поочередное вычисление каждого столбца. Каждый новый столбец вычисляется на основе вычисленных предыдущих, при этом с каждым вычислением получается всё более точное приближение искомого решения. Когда достигнута необходимая точность, процесс вычисления прерывают и в качестве решения используют последний вычисленный столбец.

Процесс вычисления одного столбца называется итерацией.

Различают несколько основных способов итерационного решения СЛАУ:

Метод Якоби (метод простых итераций СЛАУ)

Рассмотрим систему уравнений, с коэффициентами, которые можно записать в виде матрицы:

$A=\left(\begin a_ <11>& a_ <12>& … & a_ <1n>\\ a_ <21>& a_ <22>& … & a_ <2n>\\ … & … & … & … \\ a_ & a_ & … & a_ \\ \end\right)$

Добиться такого вида от системы можно следующими способами:

Готовые работы на аналогичную тему

$B= E – D^<-1>A=D^<-1>(D-A), \overrightarrow = D^<-1>\overrightarrow;$

Процедура нахождения корней тогда запишется так:

$\overrightarrow^<(k+1)>= B\overrightarrow^ <(k)>+ \overrightarrow$

Для конкретного элемента она будет выглядеть так:

Порядок решения СЛАУ методом Якоби такой:

Метод Гаусса-Зейделя

Сами итерации в методе Гаусса-Зейделя производятся по формуле:

$(L +D)\overrightarrow^<(k+1)>=-U\overrightarrow^ <(k)>+ \overrightarrow$

Метод простых итераций: пример решения

Дана система уравнений:

Решите данную систему с помощью метода простых итераций.

Проведём 5 итераций, используя на каждой результат, полученный с предыдущей и для них получим следующую таблицу:

Рисунок 1. Таблица итераций для решения СЛАУ. Автор24 — интернет-биржа студенческих работ

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13 02 2021

Источник

3 Решение систем линейных алгебраических уравнений итерационными методами

Тема 3. Решение систем линейных алгебраических уравнений итерационными методами.

Описанные выше прямые методы решения СЛАУ не очень эффективны при решении систем большой размерности (т.е. когдо значение n достаточно велико). Для решения СЛАУ в таких случаях больше подходят итерационные методы

Здесь — приближение к решению, полученное после итерации номер n, а — точное решение СЛАУ (которое заранее неизвестно). Число итераций n=n(e), необходимое для достижения заданной точности для конкретных методов можно получить из теоретических рассмотрений (т. е. для этого имеются расчетные формулы). Качество различных итерационных методов можно сравнить по необходимому числу итераций для достижения одной и той же точности.

. (3.1)

Так, к примеру, норма матрицы А из примера 1 находится следующим образом :

.

Источник

Итерационные методы решения системы линейных алгебраических уравнений

В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.

Общие сведения об итерационных методах или методе простой итерации

Метод итерации — это численный и приближенный метод решения СЛАУ.

Метод Якоби

Элементы (компоненты) вектора d вычисляются по следующей формуле:

Расчетная формула метода простой итерации:

x ( n + 1 ) = B x ( x ) + d

Матричная запись (координатная):

Критерий окончания в методе Якоби:

Решить СЛАУ методом Якоби:

Приводим СЛАУ к удобному виду для итерации:

В таком случае, первая итерация имеет следующий внешний вид:

Аналогичным способом вычисляются приближения к решению:

Далее вычисляем нормы разности векторов:

Метод Зейделя

Метод Зейделя — метод является модификацией метода Якоби.

За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.

Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.

Решим 3 системы уравнений:

Приведем системы к удобному для итерации виду:

Отличительная особенность, условие сходимости выполнено только для первой системы:

Вычисляем 3 первых приближения к каждому решению:

Итерационный процесс разошелся.

Итерационный процесс зациклился.

Метод простой итерации

Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:

Расчетная формула имеет следующий внешний вид:

Источник

В чем суть итерационного метода решения систем линейных алгебраических уравнений

Pers.narod.ru. Обучение. Лекции по численным методам. Методы решения систем линейных алгебраических уравнений

2. Методы решения систем линейных алгебраических уравнений

К решению систем линейных алгебраических уравнений сводятся многочисленные практические задачи ( по некоторым оценкам более 75% всех задач). Можно с полным основанием утверждать, что решение линейных систем является одной из самых распространенных и важных задач вычислительной математики.

Конечно, существует много методов и современных пакетов прикладных программ для решения СЛАУ, но для того, чтобы их успешно использовать, необходимо разбираться в основах построения методов и алгоритмов, иметь представления о недостатках и преимуществах используемых методов.

Постановка задачи

Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как

,

Эту систему уравнений можно записать также в матричном виде:

,

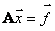
где , , .

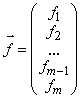
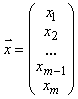
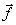
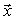
A – матрица системы, – вектор правых частей, – вектор неизвестных.

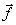
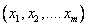
При известных A и требуется найти такие , при подстановке которых в систему уравнений она превращается в тождество.

Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.

В дальнейшем будем предполагать наличие единственного решения.

Все методы решения линейных алгебраических задач можно разбить на два класса: прямые (точные) и итерационные (приближенные).

Прямые методы решения СЛАУ

Метод Крамера

При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:

(i = 1, 2, …, m). Эти формулы позволяют находить неизвестные в виде дробей, знаменателем которых является определитель матрицы системы, а числителем – определители матриц A_i, полученных из A заменой столбца коэффициентов при вычисляемом неизвестном столбцом свободных членов. Так А₁ получается из матрицы А заменой первого столбца на столбец правых частей f.

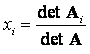
Например, для системы двух линейных уравнений

Размерность системы (т.е., число m) является главным фактором, из–за которого формулы Крамера не могут быть использованы для численного решения СЛАУ большого порядка. При непосредственном раскрытии определителей решение системы с m неизвестными требует порядка m!*m арифметических операций. Таким образом, для решения системы, например, из m = 100 уравнений потребуется совершить 10 158 вычислительных операций (процесс займёт примерно 10 19 лет), что не под силу даже самым мощным современным ЭВМ

Метод обратной матрицы

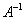
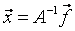
Если det A ≠ 0, то существует обратная матрица . Тогда решение СЛАУ записывается в виде: . Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция.

Метод Гаусса

Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений

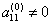
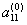
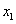
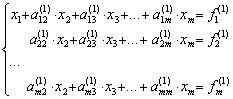
первый элемент . Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на и исключим x₁ из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при в соответствующей строке. Получим

.

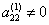
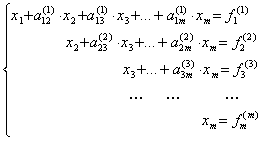
Если , то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей

.

Из нее в обратном порядке находим все значения x_i:

.

Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных – обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:

, j = i+1,i+ 2, …, m;

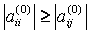
т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a₁₁ был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x₁ из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.

Рассмотрим применение метода Гаусса с выбором главного элемента на примере следующей системы уравнений:

Исключим 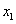из второго и третьего уравнений с помощью первого. Во втором уравнении исключать не надо. Для исключения из третьего уравнения умножим первое на 0.5 и сложим с третьим:

Рассмотрим второе и третье уравнения. Максимальный по модулю элемент при 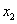в третьем. Поэтому поместим его на место второго:

Обратный ход: .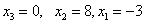

Такая перестановка уравнений необходима для того, чтобы уменьшить влияние ошибок округления на конечный результат.

Часто возникает необходимость в решении СЛАУ, матрицы которые являются слабо заполненными, т.е. содержат много нулевых элементов. В то же время эти матрицы имеют определенную структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов вместо метода Гаусса можно использовать более эффективные методы. Например, метод прогонки, который мы рассмотрим позже при решении краевой задачи для обыкновенного дифференциального уравнения второго порядка.

Итерационные методы решения линейных алгебраических систем

Метод простой итерации или метод Якоби

Напомним, что нам требуется решить систему линейных уравнений, которая в матричном виде записывается как:

,

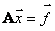
где , , .

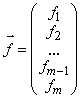
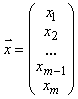
Предположим, что диагональные элементы матриц A исходной системы не равны 0 (a_ii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x₁, второе относительно x₂ и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:

(1),

Теперь, задав нулевое приближение 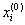, по рекуррентным соотношениям (1) можем выполнять итерационный процесс, а именно:

(2)

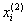
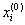
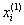
Аналогично находятся следующие приближения , где в (2) вместо необходимо подставить .

Или в общем случае:

. (3)

или

Условие окончания итерационного процесса .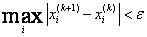

Достаточное условие сходимости: Если выполнено условие диагонального преобладания, т.е. 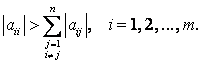, то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.

Замечание. Указанное выше условие сходимости является достаточным, т.е. если оно выполняется, то процесс сходится. Однако процесс может сходиться и при отсутствии диагонального преобладания, а может и не сойтись.

Решить систему линейных уравнений с точностью :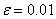

Источник

СРАВНЕНИЕ ПРОСТЫХ И ИТЕРАЦИОННЫХ МЕТОДОВ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Решение систем линейных алгебраических уравнений – одна из основных задач вычислительной линейной алгебры. Хотя задача решения системы линейных уравнений сравнительно редко представляет самостоятельный интерес для приложений, от умения эффективно решать такие системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ. Значительная часть численных методов решения различных (в особенности – нелинейных) задач включает в себя решение систем линейных уравнений как элементарный шаг соответствующего алгоритма. Мы сравним два метода решения систем линейных уравнений – метод Гаусса и метод простых итераций.

Метод Гаусса

Одним из самых распространенных методов решения систем линейных уравнений является метод Гаусса. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.

Вычисления с помощью метода Гаусса заключаются в последовательном исключении неизвестных из системы для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.

Рассмотрим простейший вариант метода Гаусса, называемый схемой единственного деления.

1-й шаг. Целью этого шага является исключение неизвестного x₁ из уравнений с номерами i = 2, 3, …, n. Предположим, что коэффициент a₁₁ 0. Будем называть его главным элементом 1-го шага.

называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, …, n-го уравнений системы первое уравнение, умноженное соответственно на q₂₁, q₃₁, …, q_n1.

Это позволит обратить в нуль коэффициенты при x₁ во всех уравнениях, кроме первого.

В результате получим эквивалентную систему

2-й шаг. Целью этого шага является исключение неизвестного x₂ из уравнений с номерами i = 3, 4, …, n. Пусть a₂₂ (1) ≠ 0, где a₂₂ (1) – коэффициент, называемый главным (или ведущим) элементом 2-го шага. Вычислим множители 2-го шага

и вычтем последовательно из третьего, четвертого, …, n-го уравнения системы второе уравнение, умноженное соответственно на q₃₂, q₄₂, …, q_m2. В результате получим систему

Аналогично проводятся остальные шаги. Опишем очередной k-й шаг.

k-й шаг. В предположении, что главный (ведущий) элемент k-го шага a_kk (k–1) отличен от нуля, вычислим множители k-го шага

и вычтем последовательно из (k + 1)-го, …, n-го уравнений полученной на предыдущем шаге системы k-e уравнение, умноженное соответственно на q_k+1,k, q_k+2,k, …, q_nk.

Матрица A (n-1) которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.

Обратный ход. Из последнего уравнения системы находим xn. Подставляя найденное значение xn в предпоследнее уравнение, получим x_n–1. Осуществляя обратную подстановку, далее последовательно находим x_n–1, x_n–2, …, x₁. Вычисления неизвестных здесь проводятся по формулам

Метод простых итераций

Для того чтобы применить метод простой итерации, необходимо систему уравнений

с квадратной невырожденной матрицей привести к виду

где – квадратная невырожденная матрица с элементами

Существуют различные способы приведения системы (1) к виду (2). Рассмотрим самый простой.

Представим систему в развернутом виде:

Из первого уравнения системы (3) выразим неизвестную :

из второго уравнения – неизвестную :

и т. д. В результате получим систему:

Матричная запись системы (4) имеет вид (2). На главной диагонали матрицы находятся нулевые элементы, а остальные элементы вычисляются по формулам:

Очевидно, что диагональные элементы матрицы должны быть отличны от нуля. Выберем произвольно начальное приближение. Обычно в качестве первого приближения берут или . Подставим начальное приближение в правую часть (4). Вычисляя левые части, получим значения . Продолжая этот процесс дальше, получим последовательность приближений, причем приближение строится следующим образом:

Последняя система представляет собой расчетные формулы метода простой итерации.

Сходимость метода простой итерации.Известно следующее достаточноеусловие сходимости метода простой итерации.

Если элементы матрицы удовлетворяют условию:

Необходимо помнить, что условие сходимости (6) является лишь достаточным. Его выполнение гарантирует сходимость метода простых итераций, но его невыполнение, вообще говоря, не означает, что метод расходится.

Справедлива следующая оценка погрешности:

Правую часть оценки (7) легко вычислить после нахождения очередного приближения.

В других случаях использование последнего критерия (8) неправомерно и может привести к преждевременному окончанию итерационного процесса.

Заключение

Анализируя результаты, полученные с помощью программ, можно сделать следующие выводы.

Метод Гаусса дает точное решение системы алгебраических уравнений, но требует перед своим применением дополнительные преобразования – проверку на наличие нулевых диагональных элементов, впрочем, как и метод простых итераций.

Во-первых, количество итераций сильно зависит от матрицы А исходной системы уравнений вида Ax=b. Чем ближе диагональные элементы матрицы А к нулю, тем больше итераций требуется для того, чтобы решить исходную систему линейных алгебраических уравнений.

Во-вторых, на количество шагов влияет начальное приближение. Чем оно ближе к точному решению, тем меньше требуется шагов для сходимости метода. Следует отметить, что в рассматриваемых примерах достаточно точное начальное приближение требует количества итераций приблизительно в 1,7-2,0 раза меньше, чем произвольное, достаточно далеко отстоящее от точного решения, приближение.

Метод простой итерации сходится быстро, если диагональные элементы матрицы А системы Ax=b близки к единице, а остальные – близки к нулю, и приближение достаточно близко к точному решению.

Список литературы:

Демидович Б.П. Численные методы анализа / Б.П. Демидович, И.А. Марон, Э.З. Шувалова. – М.: Наука, 1976. – 368с.

Мэтью Д., Финк К. Численные методы. Использование MATLAB (3-е издание). – СПб. : Вильямс, 2002. – 720 с.

Источник