в чем суть аксиоматического способа построения теории

Сущность аксиоматического метода в построении теории

При аксиоматическом построении какой-либо математической теории соблюдаются определенные правила:

— некоторые понятия теории выбираются в качестве основных и принимаются без определения;

— каждому понятию теории, которое не содержится в списке основных, дается определение; в нем разъясняется смысл понятия с помощью основных и предшествующих данному понятий;

— формулируются аксиомы – предложения, которые в данной теории принимаются без доказательства; в них раскрываются свойства основных понятий;

— каждое предложение теории, которое не содержится в списке аксиом, должно быть доказано; такие предложения называют теоремамии доказывают их на основе аксиом и теорем, предшествующих рассматриваемой.

Если построение теории осуществляется аксиоматическим методом, т.е. по названным выше правилам, то говорят, что теория построена дедуктивно.

При аксиоматическом построении теории по существу все утверждения выводятся путем доказательства из аксиом. Поэтому к системе аксиом предъявляются особые требования. Прежде всего, она должна быть непротиворечивой и независимой.

Система аксиом называется непротиворечивой, если из нее нельзя логически вывести два взаимно исключающих друг друга предложения

Если система аксиом не обладает этим свойством, она не может быть пригодной для обоснования научной теории.

Непротиворечивая система аксиом называется независимой, если никакая из аксиом этой системы не является следствием других аксиом этой системы.

Аксиоматическое построение системы натуральных чисел осуществляется по сформулированным правилам. Изучая этот материал, мы должны увидеть, как из основных понятий и аксиом можно вывести всю арифметику натуральных чисел. Конечно, его изложение в данной курсе будет не всегда строгим – некоторые доказательства мы опускаем в силу большой сложности, но каждый такой случай будем оговаривать.

Еще один пример аксиоматического построения теории – геометрия Евклида и геометрия Лобачевского.

Дата добавления: 2016-05-11 ; просмотров: 1657 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Презентация на тему:»Аксиоматический способ построения теории»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Аксиоматический способ построения теории Преподаватель: Степанян Л.У. ГБПОУ КК «Краснодарский педагогический колледж»

К началу III в. до н. э. в работах древнегреческого ученого Аристотеля была сформулирована идея построения научной теории. Применительно к геометрии ее реализовал Евклид в своей работе «Начала». На основании накопленных к тому времени фактов и знаний он выделил и сформулировал несколько утверждений (постулатов), принимаемых без доказательств, из которых выводились их логические следствия в виде теорем. Историческая справка

Система Евклида явилась первым опытом применения аксиоматического метода и просуществовала без изменений до XIX века н. э. Однако она обладала рядом недостатков с современной точки зрения на аксиоматический метод, и на рубеже XIX–XX веков была построена геометрическая система, свободная от этих недостатков. Историческая справка

Суть аксиоматического метода построения научной теории состоит в следующем: перечисляются основные (неопределяемые) понятия, все вновь возникающие понятия должны быть определены через основные понятия и понятия, определенные ранее. Суть метода

Основные понятия делятся на два вида: одни обозначают объекты, которыми занимается теория, другие обозначают отношения между ними. Так, точка и прямая – это объекты геометрии, а то, что точка принадлежит прямой, – отношение между ними. Основные понятия

Необходимость введения основных понятий очевидна, так как процесс, состоящий в том, чтобы определить одни объекты через другие, более простые, а эти в свою очередь через еще более простые, не будет ограничен до тех пор, пока некоторые объекты не будут считаться неопределимыми. Основные понятия

Аксиомы – предложения, принимаемые без доказательства. Доказывая какое-либо утверждение, опираются на некоторые предпосылки, которые считаются известными. Но эти предпосылки необходимо в свою очередь обосновать, опираясь на другие, и т. д. Чтобы оборвать эту бесконечную последовательность, вводят аксиомы – предпосылки, которые принимаются за исходные и составляют основу для доказательства теорем. Все остальные предложения должны являться логическим следствием аксиом или ранее доказанных утверждений. Список основных понятий и формулировки аксиом составляет основу теории и, в частности, планиметрии. Необходимо отметить, что основные понятия и аксиомы (назовем их кратко системой) вовсе не обязательно имеют отношение к окружающему нас реальному миру (пример такой системы – система неевклидовой геометрии). Они являются основой абстрактной теории, которая выводится как логическое их следствие, безотносительно к тому, верна исходная система или нет с нашей точки зрения. Аксиомы предпосылки, которые принимаются за исходные

Для того чтобы абстрактная теория приобрела определенный смысл, необходимо найти объект-модель, т.е. указать систему конкретных объектов и отношений между ними так, чтобы соблюдались установленные аксиомы. Такую модель иначе называют еще интерпретацией аксиоматики. Таким образом, изучаемая нами геометрия является моделью утвержденной ранее системы, в которой точку мы представляем как идеализацию следа остро отточенного карандаша, прямую – как идеализацию туго натянутой нити, а плоскость – как идеализацию гладкой поверхности стола. Геометрия модель аксиоматической системы

Для отвлеченной аксиоматики неизвестно, могут ли выводы из нее привести к противоречию. Такая аксиоматика, заключающая в себе противоречие, заведомо не может реализоваться и не имеет смысла. Таким образом, первое условие для любой системы аксиом – это ее непротиворечивость. Вопрос о противоречивости системы решается представлением ее модели. Непротеворечивость системы аксиом

Другой вопрос, касающийся системы аксиом, – это желательная их независимость. Система аксиом называется независимой, если ни одна из них не является логическим следствием остальных. К примеру, независимость аксиомы о параллельных прямых в рамках аксиоматики евклидовой геометрии удалось установить только в XIX веке, после двух тысячелетий попыток вывести ее как следствие других аксиом системы. Независимость системы аксиом

Доказательство независимости данной аксиомы в системе достигается указанием модели, в которой выполняются все аксиомы, кроме данной, которая заменяется ее отрицанием. Далее желательно, чтобы система аксиом была полной, то есть такой, что добавление к ней новой аксиомы делает новую систему аксиом зависимой. Система аксиом геометрии является полной, но это скорее исключение, чем правило: обычно системы аксиом оказываются неполными. Полнота системы аксиом

К середине XIX века, как уже было отмечено, основания евклидовой геометрии оставались на том же уровне, как они были изложены в работах Евклида. Однако общая тенденция к повышению математической строгости во второй половине XIX века побудила многих авторов к пересмотру основ геометрии с целью предложить полную, непротиворечивую, независимую систему аксиом. Наибольшее признание среди различных сформулированных систем получила аксиоматика немецкого математика Давида Гильберта, в его книге «Основания геометрии» в 1899 г. Строгость системы с Давидом Гильбертом

Ему удалось построить аксиоматику геометрии, расчлененную настолько естественным образом, что логическая структура геометрии становилась совершенно прозрачной: три группы аксиом управляют каждая своим основным отношением – принадлежности, порядка, равенства. Такое расчленение позволило, во-первых, формировать аксиомы кратким и простым образом; во-вторых, исследовать, как далеко можно развить геометрию, если положить в основу не всю аксиоматику, а только ту или иную ее группу. Система задавала действительно абстрактную теорию, в которой объекты и отношения между ними – это просто какие-то мыслимые «вещи», про которые известно только то, что они удовлетворяют аксиомам. Какую геометрию построил Д.Гильберт

Наряду с системой аксиом Гильберта можно назвать и другие варианты аксиоматики евклидовой геометрии: аксиоматика, предложенная в 1904 году Фридрихом Шуром и основанная на понятии движения (наложения) (эта идея используется в учебнике геометрии для средних школ в России, изданного под научным руководством академика А. Н. Тихонова), аксиоматика, основанная на понятии о численном расстоянии, предложенная тогда же Вениамином Федоровичем Каганом, векторная аксиоматика Германа Вейля и др. Другие варианты аксиоматики евклидовой геометрии

Несмотря на то, что вопрос о формулировке непротиворечивой, полной и независимой системы аксиом геометрии был решен, выбор «удобной» системы остается открытым еще и с точки зрения методики и наглядности изложения материала, т. е. с точки зрения педагогики. В связи с этим необходимо заметить, что приведенная в этом курсе система аксиом, так же, как и в других учебниках для средних школ, не является полной. Так, в частности, ниоткуда не следует, что между двумя данными точками прямой лежит еще точка этой прямой. Нам кажется это очевидным, так как прямая, по нашим представлениям, сплошная, непрерывная, без «дыр». Но это представление должно получить точное определение в виде свойства прямой. Аксиома, задающая это свойство, есть, и она называется «аксиомой непрерывности». Вводится понятие «аксиомы непрерывности»

Термин «натуральное число» впервые употребил в V веке римский ученый А. Боэций, который известен как переводчик работ известных математиков прошлого на латинский язык и как автор книги «О введении в арифметику», которая до XVI века была образцом для всей европейской математики. Арифметика

Во второй половине XIX века натуральные числа оказались фун­даментом всей математической науки, от состояния которого зависела и прочность всего здания математики. В связи с этим появилась необ­ходимость в строгом логическом обосновании понятия натурального числа, в систематизации того, что с ним связано. Так как математика XIX века перешла к аксиоматическому построению своих теорий, то была разработана аксиоматическая теория натурального числа. Большое влияние па исследование природы натурального числа оказала и созданная в XIX веке теория множеств. Конечно, в созданных теориях понятия натурального числа и действий над ними получили большую абстрактность, но этим всегда сопровождается процесс обобщения и систематизации отдельных фактов. Арифметика

Основные понятия и аксиомы. Определение натурального числа В качестве основного понятия при аксиоматическом построении арифметики натуральных чисел взято отношение «непосредственно следовать за», заданное на непустом множестве N. Известными также считаются понятие множества, элемента множества и другие теоретико-множественные понятия, а также правила логики. Элемент, непосредственно следующий за элементом а, обозначают а’. Суть отношения «непосредственно следовать за» раскрывается в следующих аксиомах. Натуральные числа, определение

Аксиома 1. В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Будем называть его единицей, и обозначать символом 1. Аксиома 2. Для каждого элемента а из N существует единствен­ный элемент а’, непосредственно следующий за а. Аксиома 3. Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а. Аксиомы из аксиоматической теории натуральных чисел

Источник

Об аксиоматическом способе построения теории

При аксиоматическом построении какой-либо математической теории соблюдаются определенные правила:

— некоторые понятия теории выбираются в качестве основных и принимаются без определения;

— каждому понятию теории, которое не содержится в списке основ­ных, дается определение, в нем разъясняется его смысл с помощью ос­новных и предшествующих данному понятий;

— формулируются аксиомы— предложения, которые в данной тео­рии принимаются без доказательства; в них раскрываются свойства основных понятий;

— каждое предложение теории, которое не содержится в списке ак­сиом, должно быть доказано; такие предложения называют теоремамии доказывают их на основе аксиом и теорем, предшествующих рас­сматриваемой.

Если построение теории осуществляется аксиоматическим мето­дом, т.е. по названным выше правилам, то говорят, что теория по­строена дедуктивно.

При аксиоматическом построении теории по существу все утверж­дения выводятся путем доказательства из аксиом. Поэтому к системе аксиом предъявляются особые требования. Прежде всего, она долж­на быть непротиворечивой и независимой.

Система аксиом называется непротиворечивой, если из нее нельзя логически вывести два взаимно исключающих друг друга предложения.

Если система аксиом не обладает этим свойством, она не может быть пригодной для обоснования научной теории.

Непротиворечивая система аксиом называется независимой, если никакая из аксиом этой системы не является следствием других акси­ом этой системы.

Упражнения

1. В чем суть аксиоматического способа построения теории?

3. Назовите основные понятия школьного курса планиметрии. Вспомните несколько аксиом из этого курса. Свойства каких понятий в них описываются?

4. Дайте определение прямоугольника, выбрав в качестве родового понятие параллелограмма. Назовите три понятия, которые в курсе геометрии должны предшествовать понятию «параллелограмм».

5. Какие предложения называют теоремами? Вспомните, какова логическая структура теоремы и что значит доказать теорему.

Лекция 32.Аксиоматическое построение множества целых неотрица­тельных чисел

1. Основные понятия и аксиомы Пеано. Определение целого неотрицательного числа

2. Сложение целых неотрицательных чисел. Таблицы сложения и умножения.

3. Умножение целых неотрицательных чисел. Законы сложения и умножения.

Основные понятия и аксиомы. Определение натурального числа

В качестве основного понятия при аксиоматическом построении арифметики натуральных чисел взято отношение «непосредственно следовать за», заданное на непустом множестве N. Известными также считаются понятие множества, элемента множества и другие теорети­ко-множественные понятия, а также правила логики.

Элемент, непосредственно следующий за элементом а, обозначают а’.

Суть отношения «непосредственно следовать за» раскрывается в следующих аксиомах.

Аксиома 1. В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Будем назы­вать его единицей и обозначать символом 1.

Аксиома 2. Для каждого элемента а из N существует единствен­ный элемент а¢, непосредственно следующий за а.

Аксиома 3. Для каждого элемента а из N существует не более од­ного элемента, за которым непосредственно следует а.

Аксиома 4. Всякое подмножество М множества N совпадает с N, если обладает свойствами: 1) 1 содержится в М; 2) из того, что а со­держится в М, следует, что и а’ содержится в М.

Сформулированные аксиомы часто называют аксиомами Пеано.

Используя отношение «непосредственно следовать за» и аксиомы 1-4, можно дать следующее определение натурального числа.

В данном определении ничего не говорится о природе элементов множества N. Значит, она может быть какой угодно. Выбирая в качестве множества N некоторое конкретное множество, на котором зада­но конкретное отношение «непосредственно следовать за», удовле­творяющее аксиомам 1-4, мы получим модель данной системы аксиом. В математике доказано, что между всеми такими моделями можно установить взаимно однозначное соответствие, сохраняющее отноше­ние «непосредственно следовать за», и все такие модели будут отли­чаться только природой элементов, их названием и обозначением. Стандартной моделью системы аксиом Пеано является возникший в процессе исторического развития общества ряд чисел:

Каждое число этого ряда имеет свое обозначение и название, кото­рое мы будем считать известными.

Рассматривая натуральный ряд чисел в качестве одной из моделей аксиом 1-4, следует отметить, что они описывают процесс образова­ния этого ряда, причем происходит это при раскрытии в аксиомах свойств отношения «непосредственно следовать за». Так, натураль­ный ряд начинается с числа 1 (аксиома 1); за каждым натуральным числом непосредственно следует единственное натуральное число (аксиома 2); каждое натуральное число непосредственно следует не более чем за одним натуральным числом (аксиома 3); начиная от чис­ла 1 и переходя по порядку к непосредственно следующим друг за другом натуральным числам, получаем все множество этих чисел (аксиома 4). Заметим, что аксиома 4 в формализованном виде описыва­ет бесконечность натурального ряда, и на ней основано доказательст­во утверждений о натуральных числах.

Вообще моделью системы аксиом Пеано может быть любое счет­ное множество, например:

один, два, три, четыре, …

Рассмотрим, например, последовательность множеств, в которой множество <оо>есть начальный элемент, а каждое последующее мно­жество получается из предыдущего приписыванием еще одного круж­ка (рис. 108,а). Тогда N есть множество, состоящее из множеств опи­санного вида, и оно является моделью системы аксиом Пеано. Дейст­вительно, в множестве N существует элемент <оо>, непосредственно не следующий ни за каким элементом данного множества, т.е. вы­полняется аксиома 1. Если счи­тать обведенные кружки за один элемент (рис. 108.6), то для каждого

а) <о о>, <о о о>, <о о о о>, …

б) < >, < о>, < о о>, …

множества А рассматриваемой совокупности существует единст­венное множество, которое получается из А добавлением одного круж­ка, т.е. выполняется аксиома 2. Для каждого множества А существует не более одного множества, из которого образуется множество А добавле­нием одного кружка, т.е. выполняется аксиома 3. Если М Ì N и из­вестно, что множество А содержится в М, следует, что и множество, в котором на один кружок больше, чем в множестве А, также содер­жится в N, то М

N (и значит, выполняется аксиома 4).

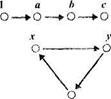каждым числом оно содержит непосредственно следующее за ним чис­ло, но оно не совпадает со всем множест­вом точек, показанных на рисунке.

Итак, мы начали аксиоматическое построение системы натураль­ных чисел с выбора основного отношения «непосредственно следо­вать за» и аксиом, в которых описаны его свойства. Дальнейшее по­строение теории предполагает рассмотрение известных свойств нату­ральных чисел и операций над ними. Они должны быть раскрыты в определениях и теоремах, т.е. выведены чисто логическим путем из отношения «непосредственно следовать за», и аксиом 1-4.

Отношение «предшествует» обладает рядом свойств. Они форму­лируются в виде теорем и доказываются с помощью аксиом 1-4.

Теорема 1. Единица не имеет предшествующего натурального числа.

Истинность данного утверждения вытекает сразу из аксиомы 1.

Доказательство. Обозначим через М множество натуральных чисел, состоящее из числа 1 и из всех чисел, имеющих предшествую­щее. Если число а содержится в М, то и число а’ также есть в N, по­скольку предшествующим для а’ является число а. Это значит, что множество М содержит 1, и из того, что число а принадлежит множе­ству М, следует, что и число а’ принадлежит М. Тогда по аксиоме 4 множество М совпадает с множеством всех натуральных чисел. Зна­чит, все натуральные числа, кроме 1, имеют предшествующее число.

Отметим, что в силу аксиомы 3 числа, отличные от 1, имеют един­ственное предшествующее число.

Аксиоматическое построение теории натуральных чисел не рас­сматривается ни в начальной, ни в средней школе. Однако те свойства отношения «непосредственно следовать за», которые нашли отраже­ние в аксиомах Пеано, являются предметом изучения в начальном курсе математики. Уже в первом классе при рассмотрении чисел пер­вого десятка выясняется, как может быть получено каждое число. При этом используются понятия «следует» и «предшествует». Каждое новое число выступает как продолжение изученного отрезка натураль­ного ряда чисел. Учащиеся убеждаются в том, что за каждым числом идет следующее, и притом только одно, что натуральный ряд чисел бесконечен. И конечно, знание аксиоматической теории поможет учителю методически грамотно организовать усвоение детьми особенности натурального ряда чисел.

Упражнения

1. Можно ли аксиому 3 сформулировать в таком виде: «Для каждого элемента а из N существует единственный элемент, за которым непосредственно следует а»?

2. Выделите условие и заключение в аксиоме 4, запишите их, используя символы Î, =>.

3. Продолжите определение натурального числа: «Натуральным числом называется элемент множества N. ».

Сложение

По правилам построения аксиоматической теории, определение сложения натуральных чисел нужно ввести, используя только отно­шение «непосредственно следовать за», и понятия «натуральное чис­ло» и «предшествующее число».

Определение. Сложением натуральных чисел называется алгеб­раическая операция, обладающая свойствами:

1) (» а Î N) а + 1 = а’, 2)(» а, b Î N) а + b’ =(а + b)’.

Теорема 3.Сложение натуральных чисел существует и оно един­ственно.

Эта теорема состоит из двух утверждений (двух теорем):

1) сложение натуральных чисел существует;

2) сложение натуральных чисел единственно.

Как правило, существование и единственность связывают вместе, но они чаще всего не зависят друг от друга. Существование какого-либо объекта не подразумевает его единственность. (Например, если вы говорите, что у вас есть карандаш, то это не значит, что он только один.) Утверждение о единственности означает, что не может сущест­вовать двух объектов с заданными свойствами. Единственность часто доказывается методом от противного: предполагают, что имеется два объекта, удовлетворяющих данному условию, а затем выстраивают цепочку дедуктивных умозаключений, приводящую к противоречию.

Чтобы убедиться в истинности теоремы 3, сначала докажем, что если в множестве N существует операция, обладающая свойствами 1 и 2, то эта операция единственная; затем докажем, что операция сложения со свойствами 1 и 2 существует.

Нетрудно убедиться в том, что 1 Î М. Действительно, из того, что а + 1= а’= аÅ 1 следует, что а + 1 = аÅ 1.

Докажем теперь, что если b Î М, то b’Î М, т.е., если а + b = а Å b, то а + b ‘ =

а Å b’. Так как а + b= а Å b, то по аксиоме 2 (а + b )’ = (а Å b)’ и тогда а + b ‘ = (а + b )’ =(а Å b)’ = а Å b’. Поскольку множество М содержит 1 и вместе с каждым числом b содержит и число b’, топо аксиоме 4, множество М совпадает с N, а значит, равенство (1) истинно для любого натурального числа b. Так как число а было выбрано произвольно, то равенство (1) верно при любых натуральных числах а и b, то есть операции + и Å на множестве N могут отличаться друг от друга только обозначениями.

Доказательство существования сложения. Покажем, что алгебраическая операция, обладающая свойствами 1 и 2, указанными в определении сложения, существует.

1) 1 + 1 =1‘- по правилу (2), т.е выполняется равенство а + 1 = а при а = 1.

Итак, 1 принадлежит множеству М.

Предположим, что а принадлежит М. Исходя из этого предположения, покажем, что и а’ содержится в М. т.е. что можно определить сложение а и любого числа b так, чтобы выполнялись условия 1 и 2.

Так как по предположению число а + b определено, то по аксиоме 2 единственным образом определяется и число (а + b )’. Проверим, что при этом выполняются условия 1 и 2:

Итак, показали, что множество М содержит 1 и вместе с каждым числом а содержит число а’. По аксиоме 4, заключаем, что множество М есть множество натуральных чисел. Таким образом, существует пра­вило, которое позволяет для любых натуральных чисел а и b одно­значно найти такое натуральное число а + b, что выполняются свой­ства 1 и 2. сформулированные в определении сложения.

Покажем, как из определения сложения и теоремы 3 можно вы­вести хорошо известную всем таблицу сложения однозначных чисел.

Условимся о следующих обозначениях: 1‘ = 2; 2′ = 3; 3′ = 4; 4′ = 5 и т.д.

1 + 1 = 1‘ на основании свойства 1 определения сложения. Но 1‘ мы условились обозначать 2. следовательно, 1+1=2.

Аналогично 2+1 = 2′ = 3; 3 + 1 = 3′ = 4 и т.д.

Рассмотрим теперь случаи, связанные с прибавлением к любому однозначному натуральному числу числа 2.

1 + 2 = 1 + 1′ = (1 + 1)’ = 2′ = 3.

Аналогично 2 + 2= 2 + 1‘ = (2 + 1)’ = 3′ = 4; 3 + 2 = 3 + 1′ = (3 + 1)’ = 4′ = 5 и т.д.

Если продолжить этот процесс, получим всю таблицу сложения однозначных чисел.

Теорема 4. (» а, b, с Î N) (а + b) + с = а + (b + с).

Теорема 5. (» а, b Î N) а + b = b + а.

Теорема 6. (» а, b Î N) а + b ¹ b.

Все доказанные свойства изучаются в начальном курсе математики и используются для преобразования выражений.

1. Верно ли, что каждое натуральное число получается из предыдущего прибавлением единицы?

2. Используя определение сложения, найдите значение выражений:

а) 2 + 3; б) 3 + 3; в) 4 + 3.

3. Какие преобразования выражений можно выполнять, используя
свойство ассоциативности сложения?

4. Выполните преобразование выражения, применив ассоциативное свойство сложения:

а) (12 + 3)+17; б) 24+ (6+19); в) 27 + 13+18.

5. Докажите, что (» а, b Î N) а + b ¹ а.

6. Выясните, как формулируются в различных учебниках математики для начальной школы:

а) коммутативное свойство сложения;

б) ассоциативное свойство сложения.

7. В одном из учебников для начальной школы рассматривается
правило прибавления числа к сумме на конкретном примере (4 + 3) + 2
и предлагаются следующие пути нахождения результата:

а) (4 + 3) + 2 = 7 + 2 = 9;

б) (4 + 3) + 2 = (4 + 2) + 3 = 6 + 3 = 9;

в) (4 + 3) + 2 = 4 + (2 + 3) = 4 + 5 =9.

Обоснуйте выполненные преобразования. Можно ли утверждать, что правило прибавления числа к сумме есть следствие ассоциативно­го свойства сложения?

8. Известно, что а + b= 17. Чему равно:

9. Опишите возможные способы вычисления значения выражения вида

а + b + с. Дайте обоснование этим способам и проиллюстрируйте их на конкретных примерах.

Умножение

По правилам построения аксиоматической теории определить умножение натуральных чисел можно, используя отношение «непосредственно следовать за» и понятия, введенные ранее.

Предварим определение умножения следующими рассуждениями.

Если любое натуральное число а умножить на 1. то получится а, т.е. имеет место равенство а × 1 = а и мы получаем правило умножения любого натурального числа на 1. Но как умножать число а на натуральное число b, отличное от 1? Воспользуемся следующим фактом:

если известно, что 7 × 5 = 35, то для нахождения произведения 7 × 6 достаточно к 35 прибавить 7, так как 7 × 6 = 7 × (5 + I) = 7 × 5 + 7. Таким образом, произведение а × b’ можно найти, если известно произведение: а × b = а × b + а.

Отмеченные факты и положены в основу определения умножения натуральных чисел. Кроме того, в нем используется понятие алгебраической операции.

Определение. Умножением натуральных чисел называется алгеб­раическая операция, обладающая свойствами:

2) (» а, b Î N) а× b’ = а × b + а.

Особенностью данного определения, так же как и определения сложения натуральных чисел, является то, что заранее неизвестно, существует ли алгебраическая операция, обладающая указанными свойствами, а если существует, то единственная ли она. В связи с этим возникает необходимость в доказательстве этого факта..

Теорема 7. Умножение натуральных чисел существует, и оно единственно.

Доказательство этой теоремы аналогично доказательству теоремы 3.

Используя определение умножения, теорему 7 и таблицу сложения, можно вывести таблицу умножения однозначных чисел. Делаем это в такой последовательности: сначала рассматриваем умножение на 1, затем на 2 и т.д.

Легко видеть, что умножение на 1 выполняется по свойству 1 в оп­ределении умножения: 1 • 1 = 1; 2 •1 = 2; 3 •1 = 3 и т.д.

Если продолжить этот процесс, получим всю таблицу умножения однозначных чисел.

Как известно, умножение натуральных чисел коммутативно, ассо­циативно и дистрибутивно относительно сложения. При аксиомати­ческом построении теории удобно доказывать эти свойства, начиная с дистрибутивности.

Но в связи с тем. что свойство коммутативности будет доказано позже, необходимо рассматривать дистрибутивность справа и слева относительно сложения.

Теорема 8. (» а, b, с Î N) (а + b) • с = а • с + b • с.

Теорема 9. (» а, b, с Î N) с •(а + b) = с • а + с • b

Это свойство дистрибутивности слева относительно сложения. Доказывается оно аналогично тому, как это сделано для дистрибутивности справа.

Теорема 10. (» а, b, с Î N) (а • b) • с = а • ( b • с).

Это свойство ассоциативности умножения. Его доказательство основывается на определении умножения и теоремах 4- 9.

Теорема 11.(» а, b Î N) а • b = b • а.

Доказательство этой теоремы по форме аналогично доказательству коммутативного свойства сложения.

Поход к умножению, рассматриваемый в аксиоматической теории, является основой обучения умножению в начальной школе. Умножение на 1, как правило, определяется, а второе свойство умножения иcпользуется при составлении таблицы умножения однозначных чисел и вычислениях.

В начальном курсе изучаются все рассмотренные нами свойства умножения: и коммутативность, и ассоциативность, и дистрибутивность.

Упражнения

1.. Используя определение умножения, найдите значения выражений:
а) 3 • 3; 6) 3 • 4; в) 4 • 3.

2. Запишите свойство дистрибутивности умножения слева относительно сложения и докажите его. Какие преобразования выражений возможны на его основе? Почему возникла необходимость в рассмотрении дистрибутивности умножения слева и справа относительно сложения?

3. Докажите свойство ассоциативности умножения натуральных чисел. Какие преобразования выражений возможны на его основе? Изучается ли это свойство в начальной школе?

4. Докажите свойство коммутативности умножения. Приведите примеры его использования в начальном курсе математики.

5. Какие свойства умножения могут быть использованы при нахождении значения выражения:

а) 5 • (10 + 4); 6)125 • 15 • 6; в) (8 • 379) • 125?

6. Известно, что 37 • 3 = 111. Используя это равенство, вычислите:

а) 37 • 18; 6) 185 • 12.

Все выполненные преобразования обоснуйте.

7. Определите значение выражения, не выполняя письменных вычислений. Ответ обоснуйте:

а) 8962 • 8 + 8962 • 2; б) 63402 • 3 + 63402 • 97; в) 849 +849 • 9.

8.. Какие свойства умножения будут использовать учащиеся началь­ных классов, выполняя следующие задания:

Можно ли, не вычисляя, сказать, значения каких выражений будут одинаковыми:

а) 3 • 7 + 3 • 5; 6) 7 • (5 + 3): в) (7 + 5) • 3?

Верны ли равенства:

а) 18 • 5 • 2 = 18 • (5 • 2); в) 5 • 6 + 5 • 7 = (6 + 7) • 5;

б) (3 • 10) •17 = 3 • 10 • 17; г) 8 • (7 + 9) = 8 • 7 + 9 • 8?
Можно ли, не выполняя вычислений, сравнить значения выражений:

Лекция 33.Вычитание и деление целых неотрицательных чисел

1. Упорядоченность множества натуральных чисел.

2. Определение вычитания целых неотрицательных чисел

3. Деление целых неотрицательных чисел. Невозможность деления на нуль. Деление с остатком.

Дата добавления: 2016-05-11 ; просмотров: 4612 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник