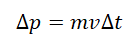в чем сущность сохранения импульса
Закон сохранения импульса. Реактивное движение
Закон сохранения импульса
Закон сохранения импульса можно наблюдать повсюду. Он достаточно точно выполняется в реальных условиях, если пренебречь сопротивлением воздуха, силами трения и т.д. Примеры проявления этого закона:
Однако, прежде чем говорить о законе сохранении импульса, рассмотрим понятие замкнутой системы.
Формулировка закона сохранения импульса (ЗСИ)
Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях этих тел между собой внутри системы.
Данный закон является следствием из второго и третьего законов Ньютона. Покажем это.
По второму закону Ньютона:
Из записанного выше следует соотношение:
m 1 v 1 → + m 2 v 2 → = m 1 v 1 ‘ → + m 2 v 2 ‘ →
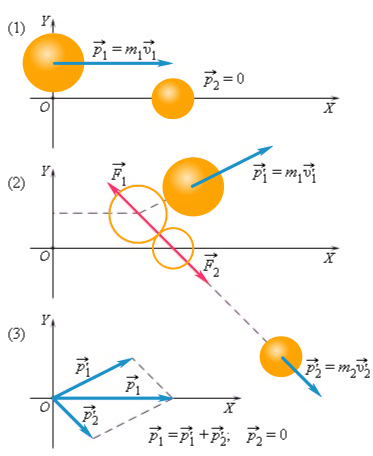
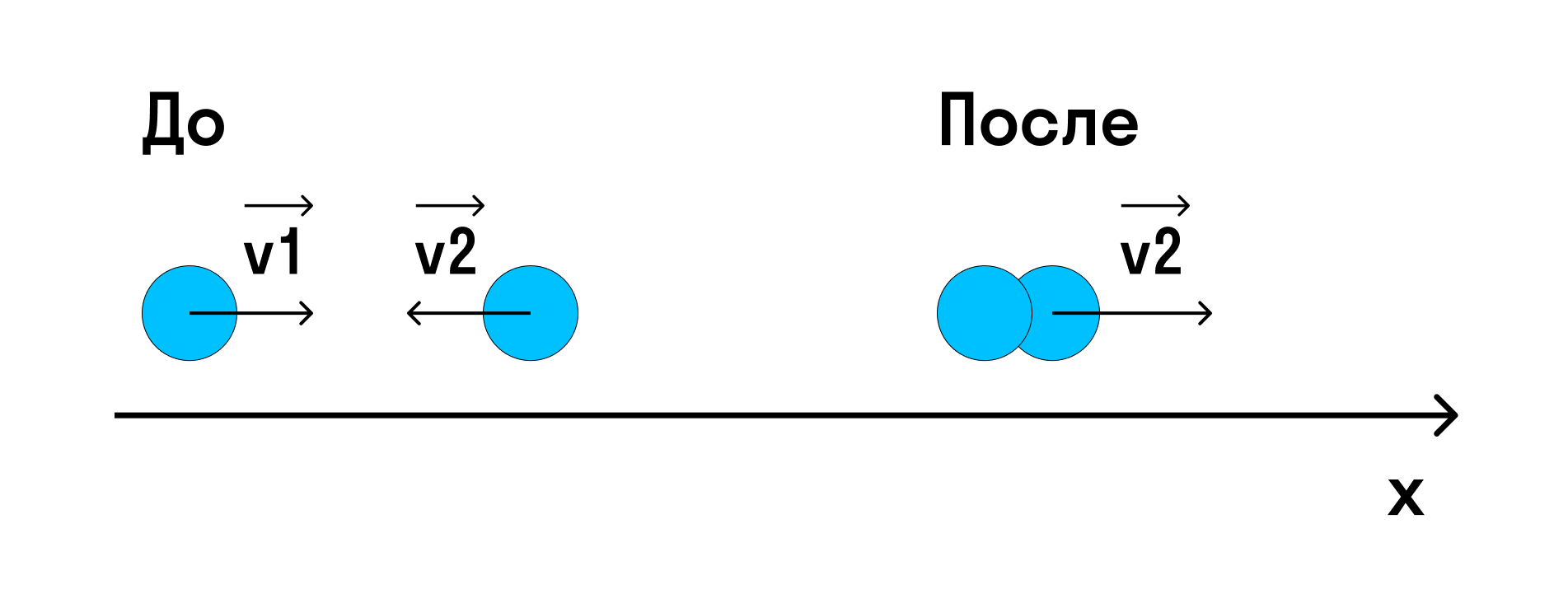
Проиллюстрируем закон сохранения импульса на примере соударения шаров разных масс. Один из шаров до удара покоился.
Как видим, после удара векторная сумма импульсов двух шаров равна первоначальному импульсу движущегося шара.
Важно! Закон сохранения выполняется и для проекций векторов на координатные оси.
Закон сохранения импульса позволяет решать задачи и находить скорости тел не зная значений действующих сил.
По закону сохранения импульса в проекции на ось OX можно записать:
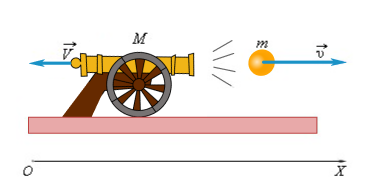
Реактивное движение
Формула для пушки и снаряда не применима к ракете, так как дает лишь приблизительное представление о движении ракеты, На самом деле вся масса газов выходит из сопла не сразу, а постепенно.
В момент t + ∆ t импульс ракеты равен:
Импульс реактивных газов:
По закону сохранения импульса:
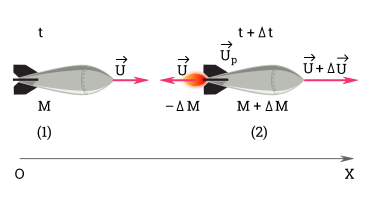
M ∆ v → ∆ t = ∆ M · u → ∆ t ( ∆ t → 0 )
Конечная скорость ракеты определяется по формуле:
Это так называемая формула Циолковского, согласно которой конечная скорость ракеты может превышать скорость истечения газов из сопла двигателя. Правда, достижение такой скорости связано с определенными сложностями. Во-первых, такими, как значительный расход топлива.
Современное ракетостроение развивается в направлении экономичных многоступенчатых ракет. Сброс отсеков с отработанным топливом позволяет значительно сократить массу ракеты и оптимизировать дальнейший расход топлива для ее разгона.
Закон сохранения импульса – формула, примеры, определение и формулировка кратко
Одним из интересных свойств материи является симметрия. Она проявляется в сохранении свойств в разных точках пространства и времени. Каждому виду симметрии соответствует свой вид сохранения. Существуют законы сохранения массы, энергии, заряда. Рассмотрим кратко один из них — закон сохранения импульса, который является следствием второго и третьего законов Ньютона.
Импульс материальной точки
Согласно первому закону Ньютона, тело, на которое не действуют никакие другие тела, либо находится в покое, либо движется прямолинейно и равномерно.
Если на тело начинает действовать сила со стороны других тел, его скорость изменяется. Изменение скорости выражается ускорением, которое можно найти с помощью второго закона Ньютона. Оно зависит от величины силы, действующей на тело, и от массы тела.
$$overrightarrow p = m overrightarrow v$$
Рис. 1. Импульс тела в физике
Импульс системы
Как правило, в реальных условиях тела существуют не изолированно, а в постоянном взаимодействии друг с другом. Кроме того, и сами тела далеко не всегда можно представить в виде материальных точек. Приходится разбивать тело на множество областей и каждую из них (и взаимодействия между ними) учитывать отдельно. Поэтому нередко требуется знать импульс не отдельных тел, а целой системы.
Импульс системы материальных точек равен векторной сумме импульсов всех точек, составляющих систему.
Рис. 2. Импульс системы тел.
Закон сохранения импульса
Если рассмотреть импульс системы материальных точек, то с помощью второго закона Ньютона можно показать, что изменение общего импульса системы зависит от векторной суммы всех сил, действующих на материальные точки в системе. В эту сумму входят силы взаимодействия точек между собой и внешние по отношению к системе силы.
Согласно третьему закону Ньютона, любое механическое взаимодействие является «двусторонним». Если одно тело действует на другое, то другое тело начинает действовать на первое с силой, равной по модулю и противоположной по направлению. Векторная сумма этих двух сил равна нулю.
А это значит, что в системе тел векторная сумма всех сил, с которыми тела действуют друг на друга, всегда равна нулю. Отсюда следует, что изменение импульса системы тел возможно только в результате действия внешних сил.
Если векторная сумма внешних сил, действующих на систему, равна нулю, то общий импульс системы не меняется.
Этот закон называется законом сохранения импульса. Формула закона сохранения импульса записывается следующим образом:
$$overrightarrow
Закон сохранения импульса является следствием второго и третьего законов Ньютона. Более глубоко физическая сущность закона сохранения импульса была обоснована Эмми Нётер в 1918 г. Сохранение импульса является следствием симметрии однородности пространства.
Безусловно, реальные системы никогда не являются замкнутыми. Поэтому закон сохранения импульса применим не всегда. К примеру, на все тела на Земле всегда действует сила тяжести. Однако если требуется определение импульса по горизонтали, то эта сила всегда компенсируется силой реакции опоры, и закон сохранения импульса выполняется с высокой точностью.
Рис. 3. Закон сохранения импульса.
Что мы узнали?
Импульс (количество движения) равен произведению массы материальной точки на её скорость. Импульс системы точек равен векторной сумме импульсов всех материальных точек, входящих в систему. Согласно закону сохранения импульса, суммарный импульс системы в отсутствие внешних сил всегда остаётся постоянным.
Импульс тела, закон сохранения импульса
теория по физике 🧲 законы сохранения
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p 1отн2— импульс первого тела относительно второго, m1 — масса первого тела, v 1отн2 — скорость первого тела относительно второго, v 1и v 2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
Изменение импульса тела
∆ p — изменение импульса тела, p — конечный импульс тела, p 0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар
Конечный импульс тела:
Модуль изменения импульса тела равен модулю его начального импульса:
Абсолютно упругий удар
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Пуля пробила стенку
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:
Радиус-вектор тела повернул на 180 градусов
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Угол падения равен углу отражения:
Модуль изменения импульса в этом случае определяется формулой:
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
F ∆t — импульс силы, ∆ p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
Отсюда скорость равна:
Импульс частицы до столкновения равен − p 1, а после столкновения равен − p 2, причём p1 = p, p2 = 2p, − p 1⊥ − p 2. Изменение импульса частицы при столкновении Δ − p равняется по модулю:
Алгоритм решения
Решение
Запишем исходные данные:
Δ p = √ p 2 1 + p 2 2
Подставим известные данные:
Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5
pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Закон cохранения импульса
9 класс, 10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Импульс: что это такое
Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.
Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.
Импульс тела
→ →
p = mv
p — импульс тела [кг*м/с]
Закон сохранения импульса
В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Закон сохранения импульса
Векторная сумма импульсов тел в замкнутой системе постоянна
А выглядит — вот так:
Закон сохранения импульса
→ → →
p1 + p2 + … + pn = const
p — импульс тела [кг*м/с]
Простая задачка
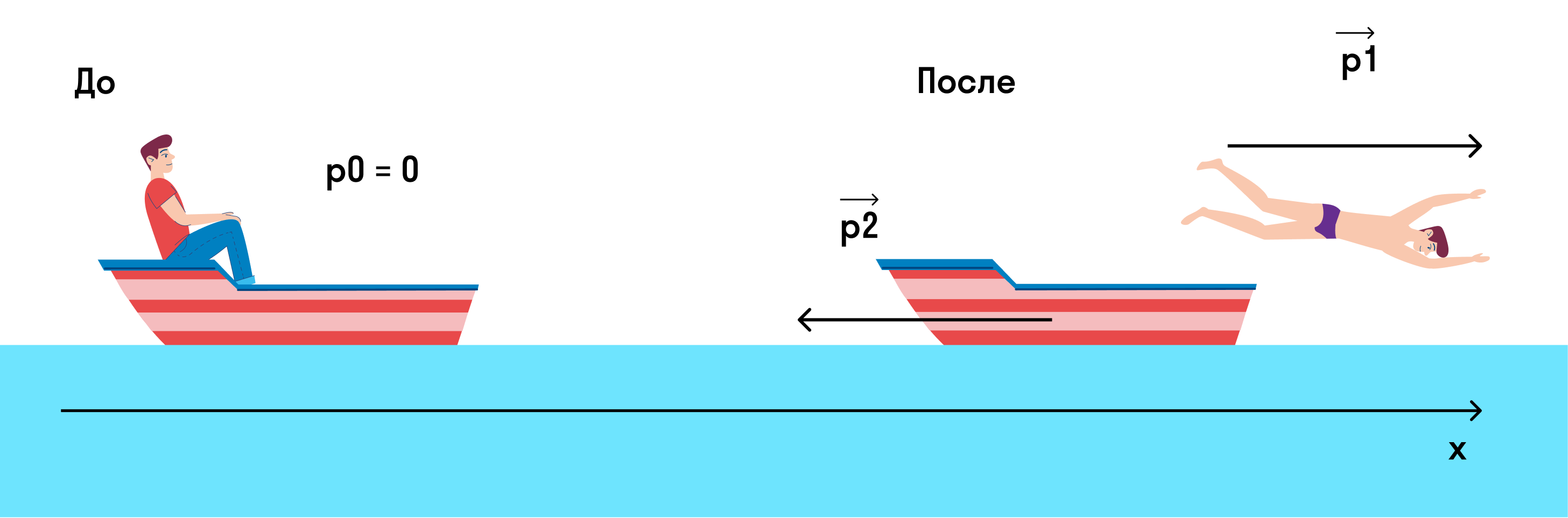
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Решение:
Запишем закон сохранения импульса для данного процесса.
p0 — это импульс системы мальчик + лодка до того, как мальчик спрыгнул,
p1 — это импульс мальчика после прыжка,
p2 — это импульс лодки после прыжка.
Изобразим на рисунке, что происходило до и после прыжка.
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
0 = p1 — p2
p1 = p2
Подставим формулу импульса.
mV1 = MV2
Выразим скорость лодки V2:
V2 = mV1/M
Подставим значения:
V2 = 45*3/270 = 3/6 = ½ = 0,5 м/с
Ответ: скорость лодки после прыжка равна 0,5 м/с
Задачка посложнее
Решение: Для данной системы выполняется закон сохранения импульса:
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.
Спроецируем импульсы на ось х:
После неупругого удара получилось одно тело массы m1 + m2, которое движется с искомой скоростью:
m1v1 — mv2 = (m1 + m2) v
Отсюда находим скорость тела, образовавшегося после удара:
v = (m1v1 — mv2)/(m1 + m2)
Переводим массу в килограммы и подставляем значения:
В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на значение получившееся значение.
Ответ: скорость системы тел после соударения равна v = 0,2 м/с.
Второй закон Ньютона в импульсной форме
Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:
Применим выражение для ускорения
Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:
В правой части находится Δv =v —v0 — это разница между конечной и начальной скоростью.
Преобразуем правую часть
Раскрыв скобки, получим
Заменим произведение массы и скорости на импульс:
То есть, вектор Δv⋅m – это вектор Δp.
Тогда второй закон Ньютона в импульсной форме запишем так
Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.
Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме
Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?
Решение:
Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).
Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.
Реактивное движение
В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.
Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.
Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:
Сила F2 называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.
Закон сохранения импульса позволяет оценить скорость ракеты.
mг vг = mр vр,
где mг — это масса горючего,
vг — скорость горючего,
vр — скорость ракеты.
Отсюда можно выразить скорость ракеты:
Скорость ракеты при реактивном движении
vр = mг vг / mр
mг — это масса горючего [кг]
vг — скорость горючего [м/с]
mр — масса ракеты [кг]
v р — скорость ракеты [м/с]
Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.