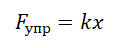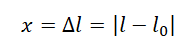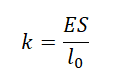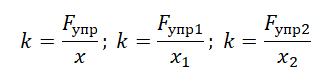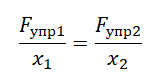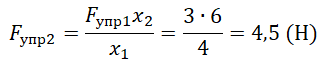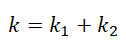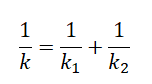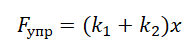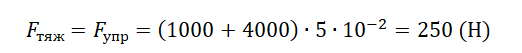в чем состоит закон гука

Сила упругости и закон Гука

теория по физике 🧲 динамика

Сила упругости — сила, которая возникает при деформациях тел в качестве ответной реакции на внешнее воздействие. Сила упругости имеет электромагнитную природу.

Деформация — изменение формы или объема тела.

Сила упругости обозначается как F _упр. Единица измерения — Ньютон (Н). Сила упругости направлена противоположно перемещению частиц при деформации.

Если после окончания действия внешних сил тело возвращает прежние форму и объем, то деформацию и само тело называю упругими. Если после окончания действия внешних сил тело остается деформированным, то деформацию и само тело называют пластическими, или неупругими.

Примеры упругой деформации:

Примеры пластической деформации:

Закон Гука

При упругой деформации есть взаимосвязь между силой упругости, возникающей в результате деформации, и удлинением деформируемого тела. Эту взаимосвязь первым обнаружил английский ученый Роберт Гук.

Модуль силы упругости, возникающей при деформации тела, пропорционален его удлинению.

x — абсолютное удлинение (деформация), k — коэффициент жесткости тела.

Абсолютное удлинение определяется формулой:

l₀ — начальная длина тела, l — длина деформированного тела, ∆l — изменение длины тела.

Коэффициент жесткости тела определяется формулой:

E — модуль упругости (модуль Юнга). Каждое вещество обладает своим модулем упругости. S — площадь сечения тела.

Важно! Закон Гука не работает в случае, если деформация была пластической.

Пример №1. Под действием силы 3Н пружина удлинилась на 4 см. Найти модуль силы, под действием которой удлинение пружины составит 6 см.

Согласно третьему закону Ньютона модуль силы упругости будет равен модулю приложенной к пружине силе. В обоих случаях постоянной величиной окажется только жесткость пружины. Выразим ее из закона Гука и применим к каждому из случаев:

Приравняем правые части формул:

Выразим и вычислим силу упругости, возникающую, когда удлинение пружины составит 6 см:

Если пружину растягивают две противоположные силы, то модули силы упругости и модули этих сил равны между собой:

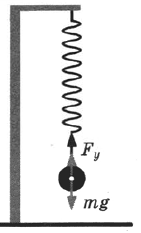
Если груз подвешен к пружине, сила упругости будет равна силе тяжести, действующей на это тело:

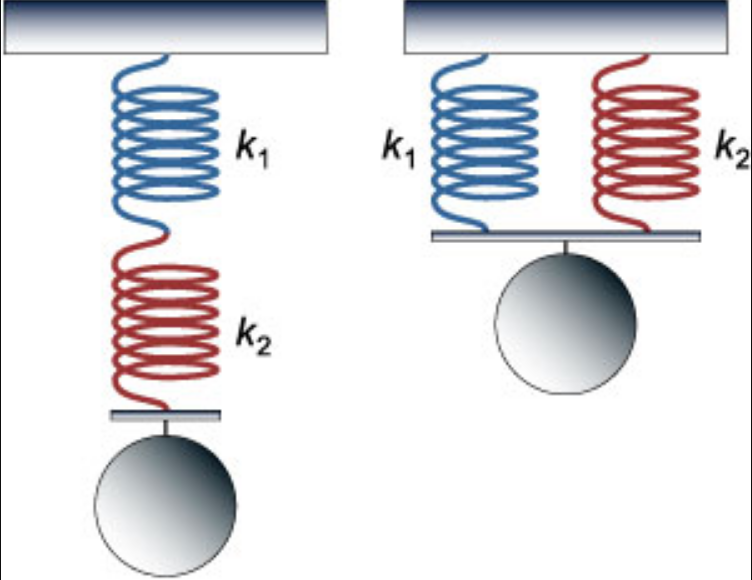
Если пружины соединены параллельно, их суммарный коэффициент жесткости будет равен сумме коэффициентов жесткости каждой из этих пружин:

Если пружины соединены последовательно, их обратное значение суммарного коэффициента жесткости будет равен сумме обратных коэффициентов жесткости для каждой из пружин:

Пример №2. Две пружины соединены параллельно. Жесткость одной из пружин равна 1000 Нм, второй — 4000 Нм. Когда к пружинам подвесили груз, они удлинились на 5 см. Найти силу тяжести груза.

Переведем сантиметры в метры: 5 см = 5∙10 –2 м.

Запишем закон Гука с учетом параллельного соединения пружин:

Модуль силы тяжести согласно третьему закону Ньютона равен модулю силы упругости. Отсюда:

На рисунке представлен график зависимости модуля силы упругости от удлинения пружины. Какова жёсткость пружины?

Источник

Закон Гука

Механика сплошных сред

Сплошная среда

Классическая механика Закон сохранения массы · Закон сохранения импульса Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнения Навье — Стокса · Уравнение диффузии · Закон Гука Известные учёные Ньютон · Гук Бернулли · Эйлер · Коши · Стокс · Навье

См. также: Портал:Физика

В словесной форме закон звучит следующим образом:

Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации

Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь — сила, которой растягивают (сжимают) стержень, — абсолютное удлинение (сжатие) стержня, а — коэффициент упругости (или жёсткости).

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения и длины ) явно, записав коэффициент упругости как

Величина называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.

Если ввести относительное удлинение

и нормальное напряжение в поперечном сечении

то закон Гука в относительных единицах запишется как

В такой форме он справедлив для любых малых объёмов материала.

Также при расчёте прямых стержней применяют запись закона Гука в относительной форме

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Содержание

Обобщённый закон Гука

В общем случае напряжения и деформации описываются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга и содержит 81 коэффициент. Вследствие симметрии тензора , а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:

где — тензор напряжений, — тензор деформаций. Для изотропного материала тензор содержит только два независимых коэффициента.

Благодаря симметрии тензоров напряжения и деформации, закон Гука может быть представлен в матричной форме.

См. также

Примечания

Ссылки

Полезное

Смотреть что такое «Закон Гука» в других словарях:

ЗАКОН ГУКА — ЗАКОН ГУКА, связь между НАПРЯЖЕНИЕМ и ДЕФОРМАЦИЕЙ в упругом материале при его растяжении. Согласно этому закону, напряжение (сила на единицу площади) пропорционально деформации (изменению в габаритах). Закон приблизителен и применим в… … Научно-технический энциклопедический словарь

закон Гука — Закон, устанавливающий пропорциональность между напряжением и деформацией (см. elastic constant) [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN Hooke s law … Справочник технического переводчика

Закон Гука — – основной закон, устанавливающий в известных пределах прямолинейную зависимость между напряженным состоянием и деформацией упругого тела. [Большая советская энциклопедия. М.: Советская энциклопедия. 1969 1978.] Рубрика термина: Теория и… … Энциклопедия терминов, определений и пояснений строительных материалов

ЗАКОН ГУКА — закон, устанавливающий линейную зависимость между (см.) твёрдого тела и приложенным механическим напряжением. Согласно З. Г. сила упругости, возникающая при деформации тела, пропорциональна удлинению тела и направлена в сторону, противоположную… … Большая политехническая энциклопедия

закон Гука — [Hooke s law] упругая деформация материала прямо пропорциональна приложенному напряжению: εн = σ/Е (для одноосного растяжения) и γ = τ/G (для сдвига), где εн относительная продольная деформация (Δl/l); ΔТ относительный сдвиг; σ нормальное… … Энциклопедический словарь по металлургии

Закон Гука — Hooke s law Закон Гука. Обобщение, применимое ко всем твердым материалам, которое показывает, что напряжение прямо пропорционально деформации и выражается как Е = constant = σ/ε = Напряжение/деформация, где Е модуль упругости (Юнга). Постоянное… … Словарь металлургических терминов

закон Гука — Huko dėsnis statusas T sritis fizika atitikmenys: angl. Hooke’s law vok. Hookesches Gesetz, n rus. закон Гука, m pranc. loi de Hooke, f … Fizikos terminų žodynas

Закон Гука — основной закон теории упругости, выражающий линейную зависимость между напряжениями и малыми деформациями в упругой среде. Установлен P. Гуком (1635 1703) в 1660 г. При растяжении стержня длиной l его удлинение пропорционально растягивающей силе… … Концепции современного естествознания. Словарь основных терминов

закон гука для рiдини при всесторонньому стисненнi — закон Гука для жидкости при всестороннем сжатии Hooke’s law for liquid in all round compression Hookesches Gesetz für die Flüssigkeit bei allseitiger Kompressibilität – змiна об’єму рiдини V при всесторонньому стисненнi прямо пропорцiйна змiнi… … Гірничий енциклопедичний словник

обобщенный закон Гука — [generalized Hooke s law] устанавливает линейную связь между напряжениями и деформациями в любых направлениях, т.е. между каждым компонентом тензора напряжений и каждым компонентом тензора деформаций: εx = [σx μ(σy σz)]E; γxy = τxy/G; εy = [σy… … Энциклопедический словарь по металлургии

Источник

Закон Гука

Закон Гука — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke). Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.

В словесной форме закон звучит следующим образом:

Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации.

Векторная формулировка закона Гука включает знак «минус», который говорит о том, что вектор деформации x всегда направлен противоположно силе упругости F:

Здесь \( F \) — сила растяжения или сжатия, \( x \) — абсолютное удлинение или сжатие, а \( k \) — коэффициент упругости (или жёсткости).

ВАЖНО Закон Гука справедлив только для упруго деформированных материалов.

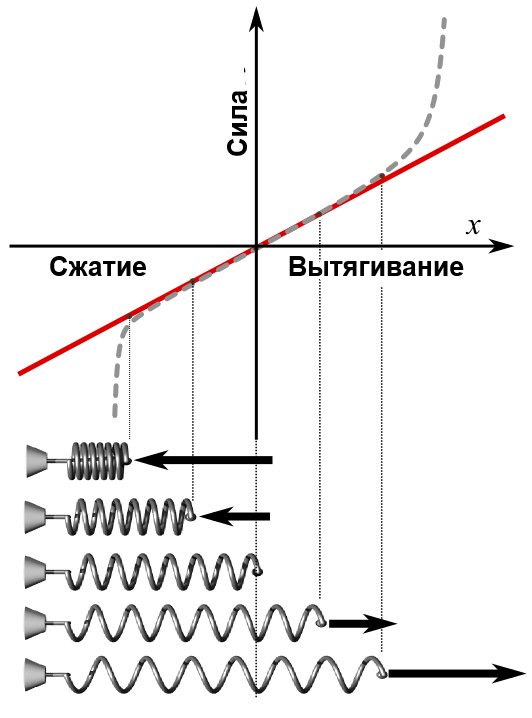
Красная линия на графике отображает изменение силы (F) в зависимости от положения в согласованности с законом Гука. Наклон соответствует постоянной пружины (k). Пунктирная линия – вид фактического графика силы. Изображения состояний пружины в нижней части отвечают некоторым точкам на графике (средняя – расслабленность)

Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь \( F \) — сила, которой растягивают (сжимают) стержень, \( \Delta l \) — абсолютное удлинение (сжатие) стержня, а \( k \) — коэффициент упругости (или жёсткости).

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L ) явно, записав коэффициент упругости как:

Величина E называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.

Если ввести относительное удлинение

и нормальное напряжение в поперечном сечении

то закон Гука в относительных единицах запишется как

В такой форме он справедлив для любых малых объёмов материала.

Также при расчёте прямых стержней применяют запись закона Гука в относительной форме

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Источник

Сила упругости. Закон Гука

Содержание

На все тела, которые находятся на Земле, действует сила тяжести. Все они стремятся под ее действием упасть вниз. Но не похоже, чтобы все в мире лежало на земле.

На еду в вашей тарелке действует сила тяжести, но она же не проваливается сквозь тарелку. На учебник на вашей парте тоже действует сила тяжести. Но стол от этого не придавливается к полу.

Значит, существует некая сила, уравновешивающая силу тяжести. В данном уроке мы узнаем, что же это за сила.

Определение силы упругости

Начнем с рассмотрения простого опыта (рисунок 1).

Рисунок 1. Деформация горизонтально расположенной доски, на которую поместили груз.

На два бруска положим доску. На доску поставим гирю. Мы увидим, что доска прогнется. Что же здесь происходит со стороны физики?

На гирю действует сила тяжести, она начинает двигаться вниз и прогибает доску. Доска деформируется из-за взаимодействия с гирей. Значит, возникает еще одна сила, с которой доска в ответ действует на гирю.

Сила тяжести, действующая на гирю, направлена вертикально вниз, а другая сила направлена вертикально вверх. Поэтому она и уравновесила силу тяжести. Нашу искомую силу называют силой упругости.

Сила упругости – это сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение.

Сила упругости – векторная величина:

В ситуации на рисунке 1, опора (доска) прогибается. Чем сильнее этот прогиб, тем больше сила упругости. Когда сила упругости и сила тяжести становятся равны, то опора и тело останавливаются. Так они приходят в равновесие.

Виды деформации

Рассмотрим следующий случай (рисунок 2). Подвесим тело на нити.

Рисунок 2. Тело, подвешенное на нити.

В таких конструкциях нить часто называют подвесом. Когда мы подвесили тело, нить начала растягиваться – в ней возникла сила упругости.

Чем больше нить растягивается, тем больше становится сила упругости. Как и в случае с опорой, как только сила упругости станет равной силе тяжести, растяжение прекратится.

Получается, что сила упругости возникает при деформации тел. Если исчезает деформация, то исчезает и сила упругости.

Иногда после таких взаимодействий тело, испытывающее деформацию, меняет свои форму и размеры – происходит неупругая (пластическая) деформация. А иногда возвращается в исходное состояние. Тогда деформация называется упругой (рисунок 3).

Рисунок 3. Упругая и пластическая деформации.

Упругая деформация – это деформация, при которой после прекращения воздействия деформирующей силы тело полностью восстановило свою форму и объем.

Пластическая деформация – это деформация, сохраняющаяся после прекращения действия деформирующей силы.

Упругая деформация бывает различных видов:

Примеры деформации разных видов

1. Играем на гитаре – кратковременно растягиваем струны

2. Садимся в автомобиль – пружины подвески сжимаются

3. Сидим на тонкой доске – доска прогибается

4. Затягиваем шуруп – происходит кручение отвёртки (хоть мы и не видим деформацию отвёртки)

5. Двигаем расшатанный стул – происходит сдвиг сиденья относительно пола

Закон Гука

От чего же зависит сила упругости? Роберт Гук, современник Ньютона, ответил на этот вопрос (рисунок 8).

Рисунок 8. Английский физик и изобретатель Роберт Гук (1635-1703). Установил зависимость силы упругости от деформации тела.

Рассмотрим опыт, изображенный на рисунке 9.

Рисунок 9. Опыт на определение зависимости силы упругости от деформации тела.

Шнур изменил свою длину после наших действий. Это изменение (удлинение шнура) мы можем найти по формуле:

Этот опыт показывает, что

Изменение длины тела при растяжении или сжатии прямо пропорционально модулю силы упругости.

Так мы подошли к закону Гука:

$$F_ <упр>= k \Delta l$$

Источник

Физика. 10 класс

Конспект урока

Перечень вопросов, рассматриваемых на этом уроке

2.Модели видов деформаций.

3. Вычисление и измерение силы упругости, жёсткости и удлинение пружины.

Сила упругости – это сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение.

Деформация – изменение формы или размеров тела, происходящее из-за неодинакового смещения различных частей одного и того же тела в результате воздействия другого тела. Виды деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.

Закон Гука – сила упругости, возникающая при деформации тела (растяжение или сжатие пружины), пропорциональна удлинению тела (пружины), и направлена в сторону противоположную направлению перемещений частиц тела

Основная и дополнительная литература по теме:

Г.Я. Мякишев., Б.Б.Буховцев., Н.Н.Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017стр. 107-112

Рымкевич А.П. Сборник задач по физике. 10-11класс.- М.:Дрофа,2009. Стр 28-29

ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.

Основное содержание урока

В окружающем нас мире мы наблюдаем, как различные силы заставляют тела двигаться, делать прыжки, перемещаться, взаимодействовать.

Однако можно также наблюдать как происходят разрушения, так называемые деформации, различных сооружений: мостов, домов, разнообразных машин.

Что необходимо знать инженеру конструктору, строителю, чтобы строить надёжные сооружения: дома, мосты, машины?

Почему деформации различны, какие виды деформации могут быть у конкретных тел? Почему одни тела после деформации могут восстановиться, а другие нет? От чего зависит и можно ли рассчитать величину этих деформаций?

Почему деформации не одинаковы у различных тел, если мы их, к примеру, сжимаем? Давайте вспомним что мы знаем о строении вещества.

Все вещества состоят из частиц. Между этими частицами существуют силы взаимодействия- эти силы электромагнитной природы. Эти силы в зависимости от расстояний между частицами проявляются, то как силы притяжения, то как силы отталкивания.

Сила упругости – сила, возникающая при деформации любых тел, а также при сжатии жидкостей и газов. Она противодействует изменению формы тел.

Мы можем наблюдать несколько видов деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.

При деформации растяжения межмолекулярные расстояния увеличиваются. Такую деформацию испытывают струны в музыкальных инструментах, различные нити, тросы, буксирные тросы.

При деформации сжатия межмолекулярные расстояния уменьшаются. Под такой деформацией находятся стены, фундаменты сооружений и зданий.

При деформации изгиба происходят неординарные изменения, одни межмолекулярные слои увеличиваются, а другие уменьшаются. Такие деформации испытывают перекрытия в зданиях и мостах.

При кручении – происходят повороты одних молекулярных слоёв относительно других. Эту деформацию испытывают: валы, витки цилиндрических пружин, столярный бур, свёрла по металлу, валы при бурении нефтяных скважин. Деформация среза тоже является разновидностью деформации сдвига.

Первое научное исследование упругого растяжения и сжатия вещества провёл английский учёный Роберт Гук.

Роберт Гук установил, что при малых деформациях растяжения или сжатия тела абсолютное удлинение тела прямо пропорционально деформирующей силе.

F _упр = k ·Δℓ = k · Iℓ−ℓ₀I закон Гука.

k− коэффициент пропорциональности, жёсткость тела.

Δℓ = I ℓ−ℓ₀ I- абсолютное удлинение пружины.

— единица измерения жёсткости в системе СИ.

При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе, а слишком большие деформации разрушают тело.

Для расчёта движения тел под действием силы упругости, нужно учитывать направление этой силы. Если принять за начало отсчёта крайнюю точку недеформированного тела, то абсолютное удлинение тела можно характеризовать конечной координатой деформированного тела. При растяжении и сжатии сила упругости направлена противоположно смещению его конца.

Закон Гука можно записать для проекции силы упругости на выбранную координатную ось в виде:

k – коэффициент пропорциональности, жёсткость тела.

x = Δℓ = ℓ−ℓ₀ удлинение тела (пружины, резины, шнура, нити….)

Графиком зависимости модуля силы упругости от абсолютного удлинения тела является прямая, угол наклона которой к оси абсцисс зависит от коэффициента жёсткости k. Если прямая идёт круче к оси силы упругости, то коэффициент жёсткости этого тела больше, если же уклон прямой идёт ближе к оси абсолютного удлинения, следует понимать, что жёсткость тела меньше.

График, зависимости проекции силы упругости на ось ОХ, того же тела от значения х.

Необходимо помнить, что закон Гука хорошо выполняется при только при малых деформациях. При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе.

Разбор тренировочных заданий

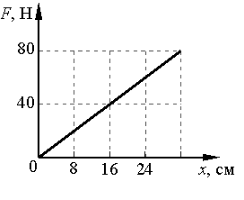
1. По результатам исследования построен график зависимости модуля силы упругости пружины от её деформации. Чему равна жёсткость пружины? Каким будет удлинение этой пружины при подвешивании груза массой 2кг?

Решение: По графику идёт линейная зависимость модуля силы упругости и удлинение пружины. Зависимость физических величин по Закону Гука:

Из формулы (1) выражаем:

Зная что F_т = mg = 20 Н, F_т = F_упр= k·Δℓ следовательно

Ответ: жёсткость пружины равна 200 Н/м, удлинение пружины равно 0,1м.

2. К системе из кубика массой 1 кг и двух пружин приложена постоянная горизонтальная сила. Система покоится. Между кубиком и опорой трения нет. Левый край первой пружины прикреплён к стенке. Удлинение первой пружины 0,05 м. Жёсткость первой пружины равна 200 Н/м. Удлинение второй пружины 0,25 м.

1. По условию задачи система находится в покое. Зная жёсткость и удлинение пружины найдём силу, которая уравновешивает приложенную постоянную горизонтальную силу.

Источник