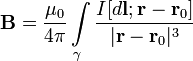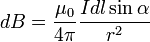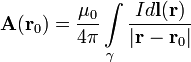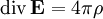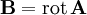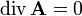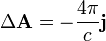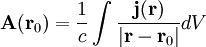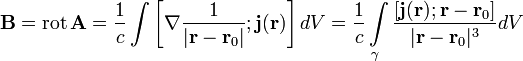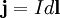в чем состоит закон био савара лапласа
Закон Био Савара Лапласа
Закон Био Савара Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.
.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
.
Закон Био-Савара-Лапласа для некоторых токов:
Магнитное поле прямого тока: 
.
Магнитное поле кругового тока: 
.
dB — магнитная индукция;
dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током;
— магнитная постоянная;
μ — относительная магнитная проницаемость (среды);
I — сила тока;
R — расстояние от провода до точки, где мы вычисляем магнитную индукцию;
α — угол между вектором dl и r.
В современной формулировке закон Био — Савара — Лапласа чаще рассматривают как следствие двух уравнений Максвелла для магнитного поля при условии постоянства электрического поля:
где квадратными скобками обозначено векторное произведение, r — положение точек контура γ, dr — вектор элемента контура (ток течет вдоль него); μ0 — магнитная постоянная; r,r0 — единичный вектор, направленный от элемента контура к точке наблюдения.
В принципе контур γ может иметь ветвления, представляя собой сколь угодно сложную сеть. В таком случае под выражением, приведенным выше, следует понимать сумму по всем ветвям, слагаемое же для каждой ветви является интегралом приведенного выше вида (контур интегрирования для каждой ветви может быть при этом незамкнутым).
В случае простого контура, ток I одинаков на всех участках контура и может быть вынесен за знак интеграла. (Это справедливо отдельно и для каждого неразветвленного участка разветвленной цепи).
Если же взять за точку отсчёта точку, в которой нужно найти вектор магнитной индукции, то формула немного упрощается:
где 
— вектор, описывающий кривую проводника с током I, r — модуль , 
— вектор магнитной индукции, создаваемый элементом проводника 
.
Пример решения задачи закона Био Савара Лапласа.
Применим закон Био — Савара — Лапласа для вычисления поля прямого тока, т. е. поля, создаваемого током, текущим по тонкому прямому проводу бесконечной длины (рис. 1). Все векторы dB в данной точке имеют одинаковое направление (в нашем случае «к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии r0 от провода. Из рис. 1 видно, что
r =R/sinα, dl =rdα/sinα = R dα/ sin 2 α.
Подставим эти значения в формулу магнитной индукции:
dB = (μ0 μ/4π) I R sinα sin 2 α dα /R 2 sin 2 α = (μ0 μ/4π) I sinα dα /R.
Угол α для всех элементов бесконечного прямого тока изменяется в пределах от 0 до π. Следовательно,
B = ∫ dB = (μ0μ/4π) I/R∫ sinα dα = (μ0 μ/4π) 2I/R.
Таким образом, магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током
B = (μ 0 μ/4π) 2I/R,
где R – кратчайшее расстояние от оси проводника.
Аналогичным образом можно найти магнитное поле в центре кругового проводника с током (рис. 2). Как следует из рисунка, все элементы кругового тока создают в центре магнитное поле одинакового направления — вдоль нормали витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin α=l) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно закону Био-Савара-Лапласа,
dB=(μ0 μ/4π) I/R 2 dl. Тогда
Следовательно, магнитная индукция поля в центре кругового проводника с током равна B = μ 0 μI/2R.
Изучаем закон Био-Савара-Лапласа
Одним из величайших достижений науки о природе 19 века является доказательство непосредственной связи между электрическим и магнитным полем. Считается, что полным описанием их взаимодействия являются уравнения Максвелла. Закон Жана-Батиста Био и Феликса Савара можно рассматривать как одно из их следствий, но он был открыт намного раньше.
История открытия закона
Электрическое и магнитное поле сначала рассматривали отдельно. Экспериментально установил факт порождения электрическим током магнитного поля датский учёный Ханс Кристиан Эрстед в 1820 году. Публичная демонстрация этого эффекта показала, что под воздействием электрического тока происходит отклонение магнитной стрелки. Открытия Эрстеда послужили основанием для исследований, проводимых Био и Саваром. Последние постарались выявить математические закономерности рассматриваемой зависимости.
Жан-Батист Био был профессором физики в Сорбонне. Узнав о достижениях Эрстеда, он с помощью коллеги Феликса Савара стал проверять воздействие проводников на различные разновидности магнитных стрелок. В итоге была найдена математически выраженная закономерность зависимости.
Формулировка закона
При описании эффектов необходимо разбить проводник, через который проходит ток, на элементарные участки, имеющие минимальную длину. Каждый из них создаёт магнитное поле. Воздействие всех участков необходимо просуммировать, чтобы узнать силу воздействия поля в конкретной точке. Это правило называется принципом суперпозиции.
Закон утверждает, что магнитное поле прямо пропорционально длине прямолинейного участка провода и силе тока, а также обратно пропорционально расстоянию до рассматриваемой точки. Оно направлено перпендикулярно электрическому току и направлению от проводника к точке измерения.
Направленность поля можно определить по правилу правой руки. Если указательный палец направлен также как сила тока, средний палец направлен на точку, где определяется магнитное поле, то большой палец, поставленный перпендикулярно к указательному и среднему, показывает направление магнитного поля.
Формула, связывающая эти величины, представлена на рисунке ниже.
Чтобы определить, какое магнитное поле создаёт весь проводник, проводится суммирование влияния каждого участка. В отдельных случаях могут быть получены относительно простые формулы, в других для получения результата нужно разбираться в методах дифференциального и интегрального исчисления.
В качестве примера можно привести формулу для кругового тока.
Для прямого тока эта формула будет выражена следующим образом:
При вычислениях надо помнить, что dl, dB и B являются векторными величинами. В первом случае величина элемента тока равна длине участка, а направление совпадает с тем, которое имеет проходящий по нему ток. Направление dB определяется по правилу правой руки, а величина — по приведённой формуле. B представляет векторную сумму всех имеющихся dB.
Закон Био-Савара и уравнения Максвелла
Экспериментально подтвержденный закон в формулировке Био-Савара был важным этапом в познании электромагнитных полей. В частности, на их основе Максвелл разработал свои уравнения, описывающие такие поля. Впоследствии была сделана математическая формулировка закона на основании этих уравнений.
Однако надо отметить, что вычисления Максвелла более сложные по сравнению с тем, как их трактует закон о магнитном поле Био-Савара. Формулировка Максвелла с учётом того, что электрическое поле постоянно, выглядит таким образом:
Эта формула может быть применена к контуру произвольной сложности. Если сила тока I является постоянной величиной, то его можно вынести за знак интеграла. В формуле использованы знаки умножения в смысле векторной операции. Если в качестве точки отсчёта будет использована точка, где происходит определение напряжённости электромагнитного поля, то формула может быть упрощена и будет выглядеть таким образом.
Особенности вычислений
При рассмотрении закона Био-Савара речь идёт о бесконечно малых проводниках. Точную их длину указать нельзя. Известно только то, что она настолько мала, что участок можно считать прямолинейным.
Ещё одно предположение состоит в том, что речь идёт об очень тонких проводах. Это означает, что их толщина пренебрежимо мала по сравнению с расстоянием от точки измерения.
Фактически вычисления основаны на том, что для малых и тонких проводников задача относительно простая, но если сложить их влияние, то будет получена точная величина магнитного поля в нужной точке.
В приведённых рассуждениях предполагалось, что для простых случаев линии напряжённости являются концентрическими окружностями. Если среда неоднородная, то магнитная проницаемость в различных точках может отличаться, что сделает форму силовых линий более сложной.
Закон в формулировке Био-Савара позволяет определить характеристики магнитного поля постоянного тока для практически любой конфигурации контура. Этот закон также носит имя Лапласа.
Био и Савар предприняли тщательные экспериментальные исследования рассматриваемого вопроса и предложили формулу для вычисления в некоторых относительно простых случаях. Лаплас обобщил полученные результаты. Он предложил использовать принцип суперпозиции и бесконечно малые участки провода для описания свойств сложных контуров. Фактически закон является плодом усилий этих трёх известных учёных, поэтому его полное название — закон Био-Савара-Лапласа.
При этом нужно учитывать, что Лаплас фактически был одним из создателей дифференциального и интегрального исчисления, принципы которого он использовал для углублённого изучения рассматриваемого закона.
Видео по теме
Закон Био—Савара—Лапласа
Закон Био—Савара—Лапласа
| Классическая электродинамика | ||||||||||||
 | ||||||||||||
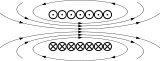| Магнитное поле соленоида | ||||||||||||
Электричество · Магнетизм
|
Закон Био́—Савара—Лапла́са — физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке. Был установлен экспериментально в 1820 году Био и Саваром. Лаплас проанализировал данное выражение и показал, что с его помощью путём интегрирования, в частности, можно вычислить магнитное поле движущегося точечного заряда, если считать движение одной заряженной частицы током.
Содержание
Формулировка
Направление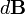 
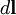
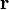
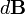
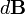
перпендикулярно 
и 
, то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление , если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора определяется выражением (в системе СИ)
Векторный потенциал даётся интегралом (в системе СИ)
Вывод из уравнений Максвелла
Закон Био — Савара — Лапласа может быть получен из уравнений Максвелла для стационарного поля. При этом производные по времени равны 0, так что уравнения для поля в вакууме примут вид (в системе СГС)
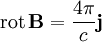
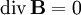
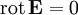
где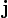 
— плотность тока в пространстве. При этом электрическое и магнитное поля оказываются независимыми. Воспользуемся векторным потенциалом для магнитного поля (в системе СГС):
Калибровочная инвариантность уравнений позволяет наложить на векторный потенциал одно дополнительное условие:
Раскрывая двойной ротор по формуле векторного анализа, получим для векторного потенциала уравнение типа уравнения Пуассона:
Его частное решение даётся интегралом, аналогичным ньютонову потенциалу:
Тогда магнитное поле определяется интегралом (в системе СГС)
аналогичным по форме закону Био — Савара — Лапласа. Это соответствие можно сделать точным, если воспользоваться обобщёнными функциями и записать пространственную плотность тока, соответствующую витку с током в пустом пространстве. Переходя от интегрирования по всему пространству к повторному интегралу вдоль витка и по ортогональным ему плоскостям и учитывая, что
получим закон Био — Савара — Лапласа для поля витка с током.
Закон Био́—Савара—Лапла́са — физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке. Был установлен экспериментально в 1820 году Био и Саваром. Лаплас проанализировал данное выражение и показал, что с его помощью путём интегрирования, в частности, можно вычислить магнитное поле движущегося точечного заряда, если считать движение одной заряженной частицы током.
Содержание
Формулировка
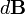
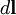
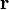
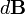
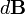
Направление перпендикулярно и , то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление , если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора определяется выражением (в системе СИ)
Векторный потенциал даётся интегралом (в системе СИ)
Вывод из уравнений Максвелла
Закон Био — Савара — Лапласа может быть получен из уравнений Максвелла для стационарного поля. При этом производные по времени равны 0, так что уравнения для поля в вакууме примут вид (в системе СГС)
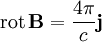
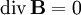
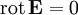
где 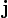— плотность тока в пространстве. При этом электрическое и магнитное поля оказываются независимыми. Воспользуемся векторным потенциалом для магнитного поля (в системе СГС):
Калибровочная инвариантность уравнений позволяет наложить на векторный потенциал одно дополнительное условие:
Раскрывая двойной ротор по формуле векторного анализа, получим для векторного потенциала уравнение типа уравнения Пуассона:
Его частное решение даётся интегралом, аналогичным ньютонову потенциалу:
Тогда магнитное поле определяется интегралом (в системе СГС)
аналогичным по форме закону Био — Савара — Лапласа. Это соответствие можно сделать точным, если воспользоваться обобщёнными функциями и записать пространственную плотность тока, соответствующую витку с током в пустом пространстве. Переходя от интегрирования по всему пространству к повторному интегралу вдоль витка и по ортогональным ему плоскостям и учитывая, что
получим закон Био — Савара — Лапласа для поля витка с током.
Вывод из Лоренц-инвариантности
Литература
Полезное
БИО ЗАКОН — БИО ЗАКОН: угол поворота плоскости поляризации линейно поляризованного света пропорционален толщине слоя оптически активного вещества, который проходит световой луч. Установлен Ж. Б. Био в 1815 … Энциклопедический словарь
Закон Ньютона — Рихмана — Закон Ньютона Рихмана эмпирическая закономерность, выражающая тепловой поток между разными телами через температурный напор. Теплоотдача это теплообмен между теплоносителем и твёрдым телом. Теплопередача это теплообмен… … Википедия
Закон Ньютона — Закон Ньютона Рихмана эмпирическая закономерность, выражающая тепловой поток между разными телами через температурный напор. Теплоотдача это процесс теплообмена между теплоносителем и твёрдым телом. Теплопередача это… … Википедия
Био Жан Батист — Био (Biot) Жан Батист (21.4.1774, Париж, ‒ 3.2.1862. там же), французский физик, геодезист и астроном, член Парижской АН (1803). Образование получил в Политехнической школе в Париже. Профессор Коллеж де Франс (1800), Парижского университета… … Большая советская энциклопедия
Био закон — закон, определяющий угол поворота φ плоскости поляризации (См. Плоскость поляризации) линейно поляризованного света, проходящего через слой аморфного вещества с естественной оптической активностью (твёрдое тело, раствор или пары): φ =… … Большая советская энциклопедия
БИО ЗАКОН — БИО ЗАКОН: угол поворота плоскости поляризации линейно поляризованного света пропорционален толщине слоя оптически активного вещества который проходит световой луч. Установлен Ж. Б. Био в 1815 … Большой Энциклопедический словарь
БИО ЗАКОН — определяет угол j вращения плоскости поляризации линейно поляризованного света, проходящего через слой некрист. в ва (жидкости или р ра в неактивном растворителе), обладающего естественной оптич. активностью: j= (a)lс, где l толщина слоя в ва, с… … Физическая энциклопедия
Био — I Био (Biot) Жан Батист (21.4.1774, Париж, 3.2.1862. там же), французский физик, геодезист и астроном, член Парижской АН (1803). Образование получил в Политехнической школе в Париже. Профессор Коллеж де Франс (1800), Парижского… … Большая советская энциклопедия
БИО ЗАКОН — угол поворота плоскости поляризации линейно поляризованного света пропорционален толщине слоя оптически активного в ва, через к рый проходит световой луч. Установлен Ж. Б. Био в 1815 … Естествознание. Энциклопедический словарь
Био-топливо — Биотопливо это топливо из биологического сырья, получаемое, как правило, в результате переработки стеблей сахарного тростника или семян рапса, кукурузы, сои. Существуют также проекты разной степени проработанности, направленные на получение… … Википедия