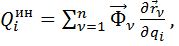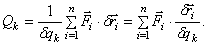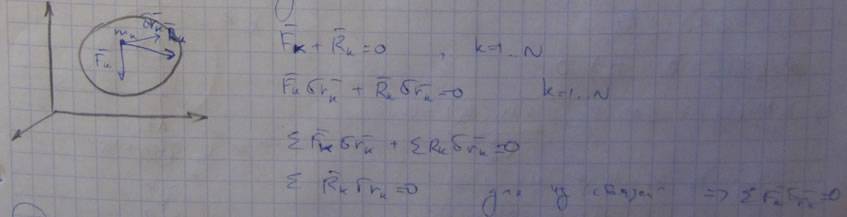в чем состоит сущность принципа возможных перемещений

Принцип возможных перемещений. Общее уравнение динамики.

Принцип возможных перемещений : для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении была равна нулю. или в проекциях: .

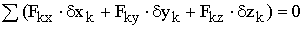
Принцип возможных перемещений дает в общей форме условия равновесия для любой механической системы, дает общий метод решения задач статики.

Если система имеет несколько степеней свободы, то уравнение принципа возможных перемещений составляют для каждого из независимого перемещений в отдельности, т.е. будет столько уравнений, сколько система имеет степеней свободы.

Принцип возможных перемещений удобен тем, что при рассмотрении системы с идеальными связями их реакции не учитываются и необходимо оперировать только активными силами.

Принцип возможных перемещений формулируется следующим образом:

Для того, чтобы матер. система, подчиненная идеальным связям находилась в состоянии покоя, необходимо и достаточно, чтобы сумма элементарных работ, производимых активными силами на возможных перемещениях точек системы была положительная

Общее уравнение динамики – при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики.

Последовательность составления:

а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции;

б) сообщают системе возможные перемещения;

в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии.

Следует отметить, что общее уравнение динамики можно применять и для систем с неидеальными связями, только в этом случае реакции неидеальных связей, таких, например, как сила трения или момент трения качения, необходимо отнести к категории активных сил.

Работа на возможном перемещении как активных, так и сил инерций, ищется также как и элементарная работа на действительном перемещении:

Возможная работа силы: .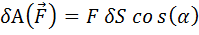

Возможная работа момента (пары сил): .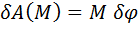

Обобщенными координатами механической системы называются независимые между собой параметры q₁, q₂, …, q_S любой размерности, однозначно определяющие положение системы в любой момент времени.

Число обобщенных координат равно S – числу степеней свободы механической системы. Положение каждой ν-й точки системы, то есть ее радиус вектор в общем случае всегда можно выразить в виде функции обобщенных координат:

(24)

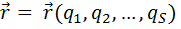
Общее уравнение динамики в обобщенных координатах выглядит в виде системы S уравнений следующим образом:

;

;

(25)

,

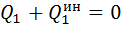
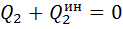
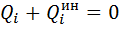
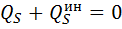
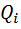
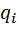
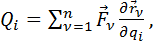
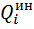
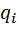
здесь – обобщенная сила, соответствующая обобщенной координате :

(26)

а – обобщенная сила инерции, соответствующая обобщенной координате :

Число независимых между собою возможных перемещений системы называется числом степеней свободы этой системы. Например. шар на плоскости может перемещаться в любом направлении, но любое его возможное перемещение может быть получено как геометрическая сумма двух перемещений вдоль двух взаимно перпендикулярных осей. Свободное твердое тело имеет 6 степеней свободы.

Обобщенные силы. Каждой обобщенной координате 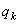можно вычислить соответствующую ей обобщенную силу Q_k.

Вычисление производится по такому правилу.

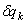
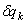
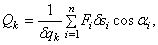
Чтобы определить обобщенную силу Q_k, соответствующую обобщенной координате q_k, надо дать этой координате приращение (увеличить координату на эту величину), оставив все другие координаты неизменными, вычислить сумму работ всех сил, приложенных к системе, на соответствующих перемещениях точек и поделить ее на приращение координаты :

(7)

где – 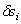перемещение i-той точки системы, полученное за счет изменения k–той обобщенной координаты.

Обобщенная сила определяется с помощью элементарных работ. Поэтому эту силу можно вычислить иначе:

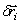
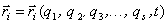
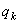
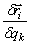
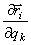
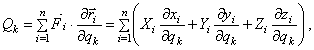
И так как есть приращение радиуса-вектора за счет приращения координаты при остальных неизменных координатах и времени t, отношение можно определять как частную производную . Тогда

(8)

где координаты точек – функции обобщенных координат (5).

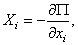
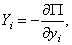
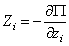
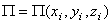
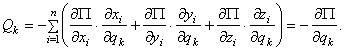
Если система консервативная, то есть движение происходит под действием сил потенциального поля, проекции которых , где , а координаты точек – функции обобщенных координат, то

(9)

Обобщенная сила консервативной системы есть частная производная от потенциальной энергии по соответствующей обобщенной координате со знаком минус.

Конечно, при вычислении этой обобщенной силы потенциальную энергию следует определять как функцию обобщенных координат

Первое. При вычислении обобщенных сил реакции идеальных связей не учитываются.

Второе. Размерность обобщенной силы зависит от размерности обобщенной координаты.

Уравнения Лагранжа 2-го рода выводятся из общего уравнения динамики в обобщенных координатах. Число уравнений соответствует числу степеней свободы:

(28)

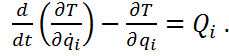
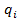
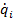
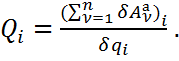
Для составления уравнения Лагранжа 2-го рода выбираются обобщенные координаты и находятся обобщенные скорости . Находится кинетическая энергия системы, которая является функцией обобщенных скоростей, и, в некоторых случаях, обобщенных координат. Выполняются операции дифференцирования кинетической энергии, предусмотренные левыми частями уравнений Лагранжа.Полученные выражения приравниваются обобщенным силам, для нахождения которых помимо формул (26) часто при решении задач используют следующие:

(29)

В числителе правой части формулы – сумма элементарных работ все активных сил на возможном перемещении системы, соответствующем вариации i-й обобщенной координаты – 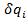. При этом возможном перемещении все остальные обобщенные координаты не изменяются. Полученные уравнения являются дифференциальными уравнениями движения механической системы с S степенями свободы.

Источник

iSopromat.ru

Принцип возможных перемещений гласит: для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.

В случае равновесия механической системы, силы, действующие на каждую точку механической системы, уравновешиваются.

Обозначая F_i — результирующую активных сил, действующих на точку, R_i — реакцию связи, получим:

Зададим системе возможное перемещение и вычислим элементарную работу всех приложенных к точке сил:

Для всей системы из «n» точек:

Для систем с идеальными связями ( ΣR_i × δS_i=0), получаем

Формула (5) выражает принцип возможных перемещений, который может быть сформулирован так: для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.

Обратными рассуждениями доказывается достаточность этого принципа.

Принцип возможных перемещений позволяет задачи статики решать методами динамики.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

В чем состоит сущность принципа возможных перемещений

Принцип возможных перемещений.

Аналитические условия равновесия механических систем были сформулированы Ж. Лагранжем в его фундаментальной работе «Аналитическая механика» (1788 г.) как «принцип возможных скоростей». В настоящее время принцип, определяющий в общей форме условия равновесия системы, называется принципом возможных перемещений, или принципом Лагранжа: чтобы данное положение механической системы со стационарными идеальными связями было положением равновесия, необходимо и достаточно, чтобы сумма элементарных работ активных сил на любом возможном перемещении системы из этого положения была равна нулю.

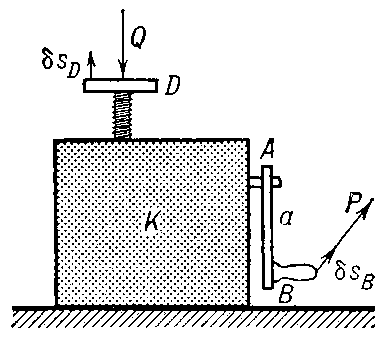
Однако принцип возможных перемещений позволяет находить и реакции идеальных связей. Для этого, в соответствии с принципом освобождаемости, связь отбрасывают, заменяя ее соответствующей реакцией. Эту реакцию включают в число активных сил. При отбрасывании связи увеличивается число степеней свободы системы. Поэтому точке приложения реакции отброшенной связи можно задать возможное перемещение. К системам с неидеальными связями принцип возможных перемещений неприменим. Однако в некоторых случаях, например при движении точки по шероховатой поверхности, связь рассматривают как идеальную, дополняя ее силой трения скольжения.

Из лекций:

Принцип возможных перемещений (Лагранжа): Для равновесной механической системы. подчиненной голономным связям (геометрические, интегрируемые кинематические = голономные), идеальным (если у какой-то связи 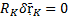(R_K тоже вектор), то связь называется идеальной), стационарным (связь называется стационарной или склерономной, если время t не входит явно в уравнение связи) и неосвобождающим (жестким) связям, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил приложенных к точкам системы была равна еулю на любом возможном перемещении системы.

Предполагаем, что одна из точек находится не в равновесии.

, что противоречит условию.

Источник

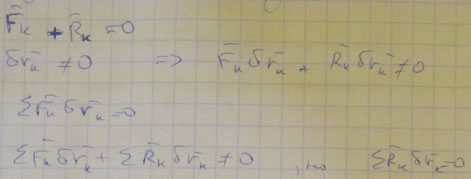
Возможных перемещений принцип

Полезное

Смотреть что такое «Возможных перемещений принцип» в других словарях:

ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП — один из вариационных принципов механики, устанавливающий общее условие равновесия механич. системы. Согласно В. п. п., для равновесия механич. системы с идеальными связями (см. СВЯЗИ МЕХАНИЧЕСКИЕ) необходимо и достаточно, чтобы сумма работ dAi… … Физическая энциклопедия

ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП — для равновесия механической системы необходимо и достаточно, чтобы сумма работ всех действующих на систему сил при любом возможном перемещении системы была равна нулю. Возможных перемещений принцип применяется при изучении условий равновесия… … Большой Энциклопедический словарь

ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП — ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП, для равновесия механической системы необходимо и достаточно, чтобы сумма работ всех действующих на систему сил при любом возможном перемещении системы была равна нулю. Возможных перемещений принцип применяется при… … Энциклопедический словарь

ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП — виртуальных скоростей принцип, дифференциальный вариационный принцип классической механики, выражающий наиболее общие условия равновесия механических систем, стесненных идеальными связями. Согласно В. п. п. механич. система находится в равновесии … Математическая энциклопедия

ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП — для равновесия механич. системы необходимо и достаточно, чтобы сумма работ всех действующих на систему сил при любом возможном перемещении системы была равна нулю. В. п. п. применяется при изучении условий равновесия сложных механич. систем… … Естествознание. Энциклопедический словарь

принцип возможных перемещений — virtualiųjų poslinkių principas statusas T sritis fizika atitikmenys: angl. principle of virtual displacement vok. Prinzip der virtuellen Verschiebungen, n rus. принцип виртуальных смещений, m; принцип возможных перемещений, m pranc. principe des … Fizikos terminų žodynas

Принцип возможных перемещений — Принцип возможных перемещений один из вариационных принципов в теоретической механике, устанавливающий общее условие равновесия механической системы. Согласно этому принципу для равновесия механической системы с идеальными связями… … Википедия

принцип виртуальных смещений — virtualiųjų poslinkių principas statusas T sritis fizika atitikmenys: angl. principle of virtual displacement vok. Prinzip der virtuellen Verschiebungen, n rus. принцип виртуальных смещений, m; принцип возможных перемещений, m pranc. principe des … Fizikos terminų žodynas

Источник

ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП

Смотреть что такое «ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП» в других словарях:

ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП — для равновесия механической системы необходимо и достаточно, чтобы сумма работ всех действующих на систему сил при любом возможном перемещении системы была равна нулю. Возможных перемещений принцип применяется при изучении условий равновесия… … Большой Энциклопедический словарь

ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП — ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП, для равновесия механической системы необходимо и достаточно, чтобы сумма работ всех действующих на систему сил при любом возможном перемещении системы была равна нулю. Возможных перемещений принцип применяется при… … Энциклопедический словарь

Возможных перемещений принцип — один из вариационных принципов механики (См. Вариационные принципы механики), устанавливающий общее условие равновесия механической системы. Согласно В. п. п., для равновесия механической системы с идеальными связями (см. Связи… … Большая советская энциклопедия

ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП — виртуальных скоростей принцип, дифференциальный вариационный принцип классической механики, выражающий наиболее общие условия равновесия механических систем, стесненных идеальными связями. Согласно В. п. п. механич. система находится в равновесии … Математическая энциклопедия

ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП — для равновесия механич. системы необходимо и достаточно, чтобы сумма работ всех действующих на систему сил при любом возможном перемещении системы была равна нулю. В. п. п. применяется при изучении условий равновесия сложных механич. систем… … Естествознание. Энциклопедический словарь

принцип возможных перемещений — virtualiųjų poslinkių principas statusas T sritis fizika atitikmenys: angl. principle of virtual displacement vok. Prinzip der virtuellen Verschiebungen, n rus. принцип виртуальных смещений, m; принцип возможных перемещений, m pranc. principe des … Fizikos terminų žodynas

Принцип возможных перемещений — Принцип возможных перемещений один из вариационных принципов в теоретической механике, устанавливающий общее условие равновесия механической системы. Согласно этому принципу для равновесия механической системы с идеальными связями… … Википедия

принцип виртуальных смещений — virtualiųjų poslinkių principas statusas T sritis fizika atitikmenys: angl. principle of virtual displacement vok. Prinzip der virtuellen Verschiebungen, n rus. принцип виртуальных смещений, m; принцип возможных перемещений, m pranc. principe des … Fizikos terminų žodynas

Источник