в чем состоит принцип независимости действия сил
Принцип независимости действия сил______________________________________
Формулировка принципа независимости действия сил______________________________________________________
Если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, согласно второму закону Ньютона, как будто других сил нет.
Ускорение, приобретаемое точкой под действием нескольких сил___________________________________________
— результирующая сила. Сила 
может быть разложена на две составляющие — тангенциальную ( 
) и нормальную 
(см. рисунок).
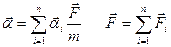
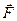
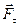
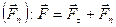
Тангенциальная и нормальная составляющие силы_________________________________________________________
Разложение силы на составляющие приводит к существенному упрощению решения задач. Например, на рисунке действующая сила F = та разложена на два компонента: тангенциальную силу FT (направлена по касательной к траектории) и нормальную силу Fn (направлена по нормали к центру кривизны).
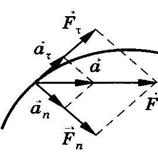
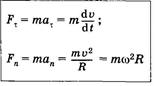
♦ Если на материальную точку действует одновременно несколько
сил, то, согласно принципу независимости действия сил, под F
во втором законе Ньютона понимают результирующую силу.
1.22 Третий закон Ньютона_______
Формулировка третьего закона Ньютона____________
Всякое действие материальных точек (тел) друг на друга имеет характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.
[F12 — сила, действующая на первую материальную точку со стороны второй; F21 — сила, действующая на вторую материальную точку со стороны первой]
Силы в третьем законе Ньютона________________________________________________________________
Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
♦ Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
Большая Энциклопедия Нефти и Газа
Принцип независимости действия сил : если на материальную точку одновременно действует несколько сил, то каждая из них сообщает точке ускорение, определяемое вторым законом Ньютона так, как если бы других сил не было. [1]
Принцип независимости действия сил ( широко используемый в сопротивлении материалов и других науках) позволяет расчленить сложную задачу на ряд простых, однако его можно использовать лишь при выполнении третьего и четвертого ддпушедий. [2]
Принцип независимости действия сил заключается в том, что каждая действующая на данное тело сила сообщает ему ускорение, величина которого не зависит ни от состояния движения тела, ни от действия на тело других сил. [3]
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которые эта точка получила бы от каждой силы в отдельности. [4]
Принцип независимости действия сил заключается в том, что каждая действующая на данное тело сила сообщает ему ускорение, величина которого не зависит ни от состояния движения тела, ни от действия на тело других сил. [5]
Принцип независимости действия сил заключается в том, что каждая действующая на данное тело сила сообщает ему ускорение, которое не зависит ни от состояния движения тела, ни от действия на тело других сил. [6]
Принцип независимости действия сил справедлив для материалов в том диапазоне, в котором они следуют закону Гука; он неприменим для многих случаев конструкционного использования термопластов, которые даже при нормальных температурах и относительно невысоких уровнях напряжений проявляют вязкоупру-гие свойства, например ползучесть. [7]
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которые эта точка получила бы от действия каждой силы в отдельности. [8]
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которыг эта точка получила бы от каждой силы в отдельности. [9]
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которую эта точка получила бы от каждой силы в отдельности. [10]
Принцип независимости действия сил и принцип сложения не применимы, когда одна из сил качественно меняет способ действия другой силы, например, в случае продольно-поперечного изгиба. [11]
Принцип независимости действия сил является основным руководящим принципом при решении подавляющего большинства задач сопротивления материалов. [12]
Принцип независимости действия сил позволяет расчленять нагрузку на отдельные части и вести расчет порознь на действие каждой из них. Простейшей базовой нагрузкой является единичная сосредоточенная сила, приложенная в определенной точке и в определенном направлении. [13]
Принцип независимости действия сил опирается на известный в физике закон Гука, характеризующий линейную зависимость между нагрузкой и деформацией. В случаях, когда процесс деформирования тела не следует закону Гука, а также в некоторых особых случаях принцип независимости действия сил применять нельзя. [14]
ПРИНЦИП НЕЗАВИСИМОСТИ ДЕЙСТВИЯ СИЛ.
Если на тело действует несколько сил, то каждая из них сообщает телу ускорение, определяемое основным законом динамики, так, как если бы других сил не было.
Например, произвольно направленную и в пространстве силу F можно представить в виде суммы ее составляющих (компонентов):
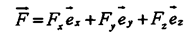
Второй закон динамики в этом случае имеет вид:
 |
 |
откуда:
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОГО ЦЕНТРА.
Моментом силы называют количественную меру вращательного эффекта, вызываемого силой. Момент силы должен определять величину этого эффекта, плоскость поворота точки и направление поворота в этой плоскости.
(рис23)
Величина момента силы равна произведению модуля силы на ее плечо h (величину перпендикуляра, опущенного из заданного центра O на линию действия силы). Если начало вектора силы совпадает с точкой А, а конец – А с точкой В, то, очевидно, плоскость поворота совпадает с плоскостью треугольника OAB (рис. 23).
 |
Очевидно, что такой вектор равен векторному произведению:
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ.
Моментом силы относительно оси называют величину, характеризующую вращательный эффект, вызываемый силой при вращении тела вокруг заданной оси.
К телу А, способному вращаться вокруг оси z приложена сила F (рис. 24). Очевидно, что эффект вызываемый силой, определяется суммой эффектов, вызываемых ее проекциями Fz и Fxy, первая из которых вращения тела вокруг оси z вызвать не может. Следовательно, момент силы относительно заданной оси определяется моментом ее проекции на плоскость, перпендикулярную оси, относительно точки Пересечения оси с плоскостью.
МОМЕНТ СИЛЫ оТНОСИТЕЛЬНО КООРДИНАТНОЙ ОСИ.
Пользуясь полученным выше результатом можно записать выражения моментов силы относительно координатных осей. Пусть к телу приложена сила F, координаты точки приложения которой равны x,y,z. Момент силы F относительно оси oz равен моменту ее проекции Fxy относительно начала координат (т. 0). В свою очередь момент Fxy равен сумме моментов сил Fx и Fy относительно того же центра. Очевидно, что плечи сил Fx и Fy численно равны координатам точки приложения силы y и x соответственно. С учетом знаков моментов этих составляющих можно записать
(рис 25)
 |
 |
Аналогично определяются моменты силы F относительно осей ОХ и ОУ:
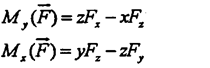Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Принцип независимости действия сил
Допущение о малости деформаций делает возможным применение принципа независимости действия сил. Этот принцип в сопротивлении материалов формулируется следующим образом: результат одновременного действия нескольких групп сил совпадает с суммой результатов, вызванных каждой группой сил в отдельности.
Для доказательства данного принципа рассмотрим двухопорную балку, изображенную на рис. 1.14. Приложим в некоторой произвольной точке силу Р1, которая вызовет в точке А перемещение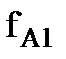 
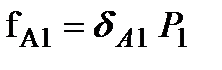
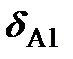
, которое равно 
, где 
— коэффициент пропорциональности. Теперь устраним действие силы Р1 и в некоторой другой произвольной точке приложим силу Р2, от действия которой точка переместится на величину 
.
Очевидно, что коэффициенты пропорциональности 
и 
не равны между собой, так как силы Р1 и Р2 приложены в разных точках балки.
| P2 |
| fA2 |
| fA1 |
| P1 |
| A |
| P2 |
| A |
| fA1+fA2 |
| P1 |
| A |
Рис. 1.14. Принцип независимости действия сил
Рассмотрим теперь совместное действие сил Р1 и Р2. Приложим сначала силу Р1, а затем, не снимая ее, силу Р2. Тогда суммарное перемещение точки А можно определить по формуле 
. Коэффициент 
будет иметь тоже значение, т.к. сила Р1 была приложена к ненагруженной балке, коэффициент же пропорциональности для силы Р2 обозначен как 
, т.к. сила Р2 приложена к системе, на которую уже действует сила Р1. Если коэффициенты 
и 
различны, то следует признать, что коэффициент 
зависит от силы Р1 (даже имеющей нулевое значение), но это противоречит принятому предположению, о линейной зависимости перемещений от действующей силы. Следовательно, 
и тогда 
. Видно, что суммарное перемещение в точке А определяется как сумма перемещений от независимых действий сил Р1 и Р2.
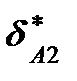
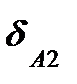
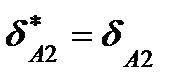
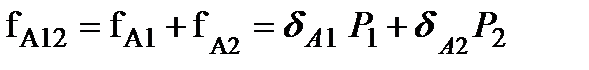
Таким образом, принцип независимости действия сил (принцип суперпозиции) сформулируем так: результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения.
При малых деформациях большинство тел можно считать линейно-упругими. Это означает, что при снятии внешней нагрузки тело полностью восстанавливает свою форму и размеры (идеальная упругость), и, кроме того, наблюдается линейная связь между силами P и смещениями D:
где k – коэффициент пропорциональности (жесткости), зависящий от вида и материала конструкции.
Действующие на упругое тело внешние силы совершают над ним работу. Эта работа, согласно закону сохранения механической энергии, переходит в потенциальную энергию упругой деформации. При сделанных выше допущениях и в предположении о квазистатическом приложении силы P потенциальная энергия легко определяется с помощью теоремы Клапейрона.
При медленном (квазистатическом) нагружении вся работа внешней нагрузки переходит в потенциальную энергию U:
.
Рассмотрим пример работы под нагрузкой консольного стержня (рис. 1.15а) или двухопорной балки (рис. 1.15б), на которые действует сила P. При этом характерные точки обеих систем переместятся на величину D, а при дополнительном нагружении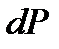 
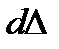
— на 
.
Рис. 1.15. К определению работы внешних сил
Элементарная работа равна (рис. 1.15в)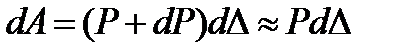 
.
Полная работа, совершаемая силой Р, вызвавшей перемещение 
, будет
.
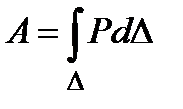
Этот интеграл представляет собой заштрихованную площадь диаграммы, и, значит, для линейно-упругой системы будет численно равен площади треугольника:
.
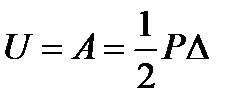
Данное равенство называется теоремой Клапейрона и имеет очень большое значение при исследовании перемещений различных упругих систем.
При действии на систему нескольких сил (n) теорема Клапейрона принимает вид:
.
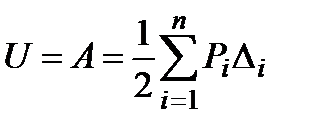
Большая Энциклопедия Нефти и Газа
Применение принципа независимости действия сил к решению задач сопротивления материалов и теории упругости дает очень много. Оно позволяет, во-первых, при большом числе внешних сил получить решение как результат наложения частных решений. [1]
Один из примеров применения принципа независимости действия сил иллюстрируется рис. 1.19, не требующим дополнительных пояснений. [3]
Таким образом, расчет на косой изгиб с применением принципа независимости действия сил сводится к расчету двух прямых изгибов. [8]
Подчеркиваем, что, говоря о действии какой-либо силы, всегда имеют в виду эту силу вместе с соответствующими ей реакциями связей. Один из примеров применения принципа независимости действия сил иллюстрирует рис. 1.18, не требующий дополнительных пояснений. [10]
Конечно, дело не в том, рассматривать ли подлежащие изучению вопросы как отдельную тему или как составную часть темы Изгиб. Не надо создавать у учащихся впечатления, что изучаются какие-то новые теоретические вопросы; просто им даются практические рекомендации по применению принципа независимости действия сил к некоторым частным задачам сопротивления материалов. [11]
Конечно, дело не в том, рассматривать ли подлежащие изучению вопросы как отдельную тему или как составную часть темы Изгиб. Не надо создавать у учащихся впечатления, что изучаются какие-то новые теоретические вопросы; просто им даются практические рекомендации по применению принципа независимости действия сил к некоторым частным задачам сопротивления материалов. [12]