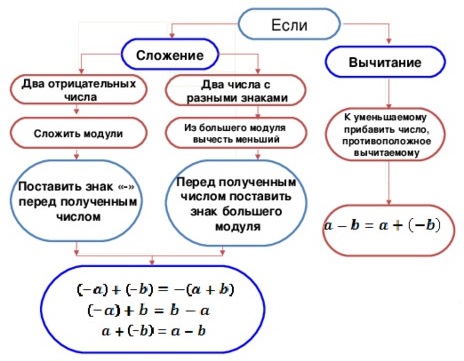
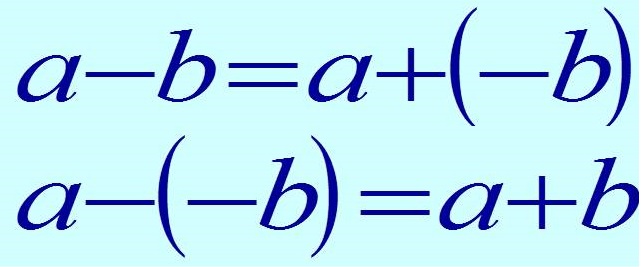в чем состоит правило сложения отрицательных чисел

Сложение чисел с разными знаками: правило, примеры

В этом материале мы расскажем, как правильно выполнять сложение отрицательного и положительного числа. Сначала мы приведем основное правило такого сложения, а потом покажем, как оно применяется при решении задач.

Основное правило сложения положительных и отрицательных чисел

Мы уже говорили ранее, что положительное число можно рассматривать как доход, а отрицательное – как убыток. Чтобы узнать величину дохода и расхода, надо смотреть на модули этих чисел. Если в итоге окажется, что наши расходы превышают доходы, то после их взаимного учета мы останемся должны, а если наоборот, то мы останемся в плюсе. Если же расходы равны доходам, то у нас будет нулевой остаток.

Используя приведенные выше рассуждения, можно вывести основное правило сложения чисел с разными знаками.

Для сложения положительного числа с отрицательным необходимо найти их модули и выполнить сравнение. Если значения окажутся равны, то мы имеем два слагаемых, которые являются противоположными числами, и их сумма будет нулевой. Если же они не равны, то нам надо учесть, что результат будет иметь тот же знак, что и большее число.

Таким образом, сложение в данном случае сводится к вычитанию из большего числа меньшего. Итог этого действия может быть разным: мы можем получить как положительное, так и отрицательное число. Нулевой результат тоже возможен.

Это правило распространяется на целые, рациональные и действительные числа.

Задачи на сложение положительного числа с отрицательным

Разберем, как применять на практике правило, озвученное выше. Возьмем для начала простой пример.

Решение

Если в условиях задачи стоят рациональные числа с разными знаками, не являющиеся при этом целыми, то для удобства расчетов нужно представить их в виде десятичных или обыкновенных дробей. Возьмем такую задачу и решим ее.

Решение

Первым делом переведем смешанное число в обыкновенную дробь. Если вы не помните, как это делается, перечитайте соответствующую статью.

Далее вычтем из большего модуля меньший (см. материал о том, как найти разность дробей с одинаковыми знаменателями):

Запишем весь ход решения:

Решение

Источник

Правило сложения отрицательных чисел и чисел с разными знаками

Для суммирования двух отрицательных чисел, необходимо:

суммировать их модули;

перед полученной суммой поставить знак «минус».

В данном случае, складываем модули 9 и 6, и перед получившимся натуральным числом 15 ставим знак «-«.

Сложение рациональных или дробных чисел выполняется аналогичным способом:

К 26,35 прибавляем 25,35 (т. е. мы складываем модули), в итоге получаем 51,75 с отрицательным значением. Перед ним ставим знак «минус».

Для суммирования натуральных чисел со знаками «+» и «-», надо:

из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;

перед полученным результатом поставить знак того слагаемого, которое имело большее значение.

61,2 + (-31,5) = + (61,2 — 31,5) = 30,5

Модуль большего числа со знаком «+», соответственно, сумма получилась положительная:

Большее число со знаком «-», поэтому заменяем плюс на минус и получаем отрицательный ответ.

Как вычитать отрицательные и положительные числа

Для нахождения разности противоположных чисел, надо к уменьшаемому прибавить вычитаемое с противоположным знаком, то есть заменить разность суммой.

Наглядно данное действие лучше представить в виде формулы:

То есть любое выражение, содержащее знаки сложения и вычитания, следует решать как сумму чисел.

-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.

Разность выражения будет положительной, если уменьшаемое больше вычитаемого, и отрицательной, если значение модуля уменьшаемого меньше вычитаемого. В случае, когда уменьшаемое и вычитаемое одинаковые, их разность будет равна нулю.

Если нужно отнять отрицательное число, то два знака «минус» подряд дают знак «плюс».

Все вышеперечисленные действия возможно выполнить на калькуляторе. Для этого достаточно ввести сначала модуль числа, потом нажать кнопку изменения знака «+/-».

Заключение

Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма.

Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.

Источник

Сложение отрицательных чисел

Что такое отрицательные числа

Отрицательное число является компонентом множества из отрицательных чисел, сформированного в процессе увеличения множества натуральных чисел.

Расширение спектра натуральных чисел потребовалось для зачисления операции вычитания в перечень полноценных арифметических действий таких, как сложение. При рассмотрении натуральных чисел можно заметить, что вычитание предполагает всегда уменьшение большего числа на меньшее число. Переместительный закон на действия с вычитанием не распространяется.

Вычитать можно любые натуральные числа, так как к натуральным числам добавили отрицательные числа и нуль. В итоге такой трансформации получилось множество, которое состояло из целых чисел. В дальнейшем числовые множества пополнились за счет рациональных и вещественных чисел, которые также могут обладать отрицательными значениями. Понятие отрицательного числа не применимо к комплексным числам.

Рассмотрим числовую ось, на которой отмечены отрицательные числа с левой стороны от нуля:

Такие числа являются противоположными. Одни числа называют положительными, а в противовес им существуют отрицательные числа. В том случае, когда n представляет собой положительное число, можно сказать, что противоположное ему число является отрицательным. Заметим, что нуль противоположен сам себе.

Положительные и отрицательные числа упорядочены, поэтому данные числа можно сравнивать между собой. Все отрицательные числа меньше по сравнению с нулем, а также меньше по сравнению с положительными числами. Рассматривая числовую ось, можно заметить, что они расположены слева по отношению к нулю.

Если число a вычитается из другого числа b, то данное действие будет равносильным сумме b с противоположным числом для a:

Сложение отрицательных чисел

Существует несколько способов сложения отрицательных чисел. К примеру, если числа по модулю обладают небольшими значениями, допускается использование координатной прямой. При этом можно представить действия, как перемещение точки, обозначающей число, по числовой оси.

Предположим, что имеется некое число 3 и отметим его на числовой оси в виде точки А.

Попробуем увеличить число 3 на положительное число 2, то есть найдем их сумму. В процессе требуется передвинуть точку А в положительном направлении на пару единичных интервалов. При перемещении в правую сторону будет установлена точка В с координатой 5.

Далее разберем пример сложения положительного и отрицательного числа:

Алгоритм действий при сложении рациональных чисел с использованием координатной прямой:

Разберем процесс сложения двух отрицательных чисел:

Упрощенным вариантом сложения рациональных чисел является применение модуля. Рассмотрим способ на конкретном примере. Предположим, что имеются два числа с одинаковыми знаками и найдем их сумму.

В первую очередь следует избавиться от знаков и суммировать модули чисел. К результату нужно дописать знак, который фигурировал в исходной записи чисел:

4 8 + 3 8 = 4 + 3 8 = 7 8

Разберем на примере сложение отрицательных чисел аналогичным способом:

Сложение чисел с одинаковыми знаками предполагает сложение модулей этих чисел и запись перед полученной суммой знака, который стоял перед слагаемыми.

Таким образом, можно вывести правило для сложения отрицательных чисел.

Найти сумму пары отрицательных чисел можно путем сложения их модулей. Перед результатом, который получился, нужно поставить знак минуса.

Описание алгоритма

Алгоритм сложения двух отрицательных чисел, в том числе, в виде дробей:

Применим алгоритм действий при выполнении упражнения:

В первую очередь сложим модули заданных чисел и перед полученным числом запишем знак минуса:

Примеры задач с ответами для 6 класса

Требуется решить примеры:

Воспользуемся правилом сложения чисел с разными знаками и алгоритмом сложения отрицательных чисел. Получим:

Необходимо выполнить вычисления:

Согласно алгоритму сложения отрицательных чисел, выполним арифметические действия:

Сложить два отрицательных числа:

Руководствуясь правилом сложения отрицательных чисел, найдем сумму их модулей:

Запишем ответ со знаком минуса:

Источник

Урок 33 Бесплатно Сложение отрицательных чисел

Вам известно, что существуют как положительные, так и отрицательные числа. Уроками ранее вы научились выполнять с положительными и отрицательными числами различные действия: определять и отмечать их на координатной прямой, находить модуль, сравнивать и складывать с помощью координатной прямой.

Операция сложения положительных чисел нам знакома уже давно.

Сегодня на уроке постараемся выяснить, возможно ли складывать отрицательные числа друг с другом и что будет результатом такого сложения.

Рассмотрим правило сложения отрицательных чисел и выясним, как изображают сумму отрицательных чисел на координатной прямой.

Разберем примеры сложения отрицательных чисел.

Правило сложения отрицательных чисел

Использование отрицательных чисел в настоящее время обычно и естественно, но такая ситуация была не всегда.

Древние вообще не пользовались отрицательными числами, считали их недопустимыми, относились к ним настороженно, существование их долгое время отрицали и все полученные отрицательные результаты вычислений считали недействительными и абсурдными.

Интересен тот факт, что осознание существования и нужности отрицательных чисел началось с представления и применения их в торговле в качестве «долга» и «убытка».

Положительные числа трактовали как «прибыль» и «имущество».

Индийский математик и астроном Брахмагупта сформулировал правила сложения и вычитания отрицательных чисел, в которых говорилось:

«Сумма двух имуществ есть имущество»

(+х) + (+х) = +Х

«Сумма двух долгов есть долг»

Таким образом, если воспринимать отрицательные числа как «долг», то в таком случае модуль отрицательного числа будет являться величиной этого долга.

Задача:

Землевладелец попросил у своего знакомого в долг 4 мешка зерна для весеннего посева, но четырех мешков ему не хватило, и он попросил в долг еще 2 мешка зерна.

Сколько мешков зерна остался должен в итоге землевладелец своему знакомому?

Решение:

Четыре мешка зерна были взяты в долг, значит, число 4 будет обозначено отрицательным числом (-4).

Два мешка зерна так же были взяты в долг, значит, число 2 тоже будет со знаком минус (-2).

Сумму двух отрицательных чисел можно записать двумя способами:

Знаки, стоящие рядом, отделяют друг от друга скобкой.

Часто скобки и знак плюс опускают, при этом запись суммы отрицательных чисел становится короче, но она равнозначна первой записи (т.е. прибавление отрицательного числа равносильно вычитанию положительного).

Итак, мы выяснили, что долг землевладельца возрос и он составил 6 мешков зерна.

Сформулируем общее правило сложения отрицательных чисел.

Чтобы сложить отрицательные числа, нужно:

1. Сложить модули отрицательных чисел

2. Поставить перед полученным числом знак минус «-»

В буквенном виде правило выглядит так:

У меня есть дополнительная информация к этой части урока!

Многие древние математические сочинения и правила были написаны в стихотворной форме, поскольку древняя математика имела прикладной характер, а стихотворения были легки для восприятия и понимания.

В учебниках правила для запоминания даются в основном строго научные и зачастую очень длинные. Несомненно мы их должны знать и понимать.

Для облегчения понимания и представления различных законов и правил современные математики часто применяют дополнительные ассоциации, стихотворные формы и другое.

Так для правила сложения отрицательных чисел тоже было придумано четверостишье. Оно звучит так:

Мало будет заботы о том:

Минус поставим вначале,

Модули сложим потом.

Рассмотрим еще несколько примеров жизненных задач, где применяется сложение отрицательных чисел.

Задача:

Игрок набрал 6 штрафных очков за первую половину турнира, затем под конец турнира совершил еще одно нарушение. Судья назначил игроку 1 штрафное очко.

Сколько штрафных очков получил игрок за весь турнир?

Решение:

Штрафные очки можно записать отрицательным числом:

Чтобы получить общее количество штрафных очков, нужно сложить все штрафы за турнир.

Воспользуемся правилом сложения отрицательных чисел.

Найдем модули отрицательных чисел:

|-6| = 6

|-1| = 1

Выполним сложение модулей чисел

6 + 1 = 7

Поставим знак минус перед полученным числом, получим (-7)

Решение задачи выглядит так:

Ответ: 7 штрафных очков получил игрок за турнир.

Задача:

Рассмотрим задачу о понижении температуры воздуха.

Решение:

Воспользуемся правилом сложения отрицательных чисел.

Найдем модули отрицательных чисел:

|-3| = 3

|-5| = 5

Выполним сложение модулей чисел

3 + 5 = 8

Поставим знак минус перед полученным числом, получим (-8)

Запись решения задачи выглядит так:

Пройти тест и получить оценку можно после входа или регистрации

Сложение отрицательных чисел с помощью координатной прямой

Сложение отрицательных чисел, небольших по модулю, легко представить на координатной прямой.

Рассмотрим сложение отрицательных чисел с помощью координатной прямой на примере задачи о понижении температуры воздуха, рассмотренной выше.

Мы уже знаем из условий задачи, что

—3ºС — температура воздуха в полдень.

По направлению координатной прямой откладываются положительные значения.

Против направления координатной прямой откладываются отрицательные значения.

Рассмотрим порядок сложения двух отрицательных чисел с помощью координатной прямой:

1. Отметить на координатной прямой точку, с координатой равной первому слагаемому

2. Переместить ее против направления координатной прямой на расстояние (количество единичных отрезков), равное модулю следующего слагаемого

3. Полученная точка на координатной прямой будет иметь значение, равное сумме отрицательных чисел

Если суммируется не два отрицательных числа, а больше, то после п.3 рассмотренного порядка сложения отрицательных чисел с помощью координатной прямой, необходимо применить п.2 для каждого следующего слагаемого.

Пример:

Попробуем разобраться с помощью координатной прямой в истинности утверждений:

Доказательство первого утверждения:

Так как слагаемые отрицательные числа, то точки, соответствующие этим числам, находятся слева от точки начала отсчета.

В результате сложения отрицательных слагаемых точка перемещается еще дальше от точки начала отсчета влево (против направления координатной прямой), что говорит об уменьшение значения суммы и о том, что значение суммы будет являться отрицательным числом.

Доказательство второго утверждения:

Отмечая точку, соответствующую первому слагаемому, откладываем влево от начала координат (против направления координатной прямой) отрезок, длина которого равна модулю этого слагаемого. В результате полученная точка смещается влево (против направления координатной прямой) на отрезок, равный модулю следующего слагаемого и т.д. Следовательно, сумма длин отрезков (а это значит, сумма модулей слагаемых) равняется модулю суммы всех слагаемых.

Пример:

OD = OA + AB + BC + CD = 2 + 2 + 3 + 3= 10

Пройти тест и получить оценку можно после входа или регистрации

Источник

Сложение отрицательных чисел: правило, примеры

В рамках этого материала мы затронем такую важную тему, как сложение отрицательных чисел. В первом параграфе мы расскажем основное правило для этого действия, а во втором – разберем конкретные примеры решения подобных задач.

Основное правило сложения натуральных чисел

Перед тем, как вывести правило, вспомним, что мы вообще знаем о положительных и отрицательных числах. Ранее мы условились, что отрицательные числа нужно воспринимать как долг, убыток. Модуль отрицательного числа выражает точные размеры этого убытка. Тогда сложение отрицательных чисел можно представить как сложение двух убытков.

Воспользовавшись этим рассуждением, сформулируем основное правило сложения отрицательных чисел.

Исходя из этого правила, можно сделать вывод, что сложение отрицательных чисел аналогично сложению положительных, только в итоге у нас обязательно должно получиться отрицательное число, ведь перед суммой модулей надо ставить знак минус.

Задачи на сложение отрицательных чисел

Во втором параграфе мы возьмем конкретные задачи, где нужно складывать отрицательные числа, и попробуем применить в них изученное правило.

Решение

От того, какие у нас числа, зависит, к чему мы можем свести действие сложения: к нахождению суммы натуральных чисел, к сложению обыкновенных или десятичных дробей. Разберем задачу с такими числами.

Решение

В итоге мы получили дробь, которую будет легко сложить с первым исходным слагаемым (если вы забыли, как правильно складывать дроби с разными знаменателями, повторите соответствующий материал).

2 5 + 136 33 = 2 · 33 5 · 33 + 136 · 5 33 · 5 = 66 165 + 680 165 = 764 165 = 4 86 105

В итоге мы получили смешанное число, перед которым нам осталось только поставить минус. На этом расчеты завершены.

Источник