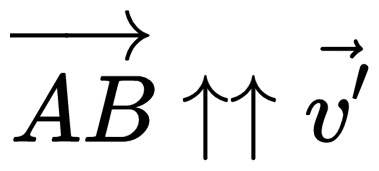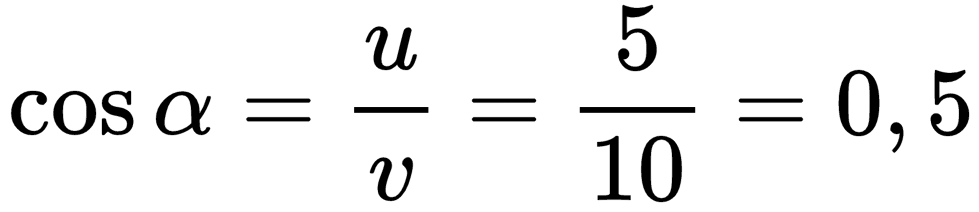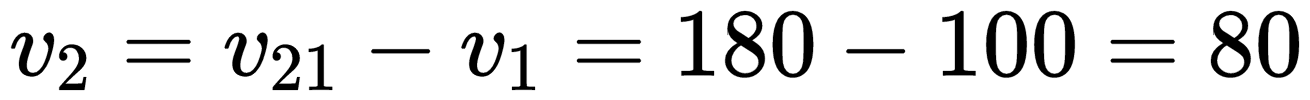в чем состоит относительность движения
Кинематика. Относительность движения.
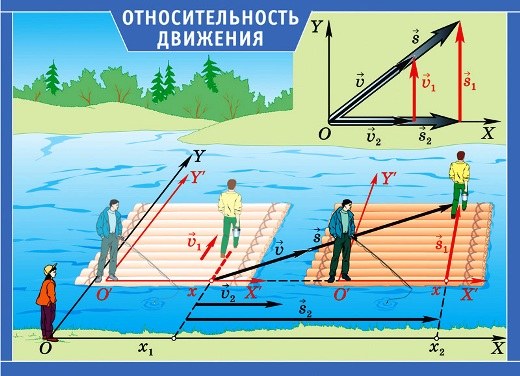
Относительность механического движения заключается в относительности скоростей перемещения тел: их скорости будут различны относительно разных систем отсчета. Например, скорость человека, едущего в поезде, или летящего самолетом, будет отличаться как по величине, так и по направлению, в зависимости от того, в какой системе отсчета эти скорости определяются: в системе отсчета, связанной с движущимся транспортным средством, или с неподвижной Землей. Различными будут также траектории и скорости движения тела в разных системах отсчета. При механическом движении относительна также траектория движения.
Пройденный телом путь тоже зависит от системы отсчета. Рассмотрев тот же пример с пассажиром в поезде можно понять, что проделанный им путь относительно поезда за время поездки равен нулю (если он за все время не передвигался по вагону), или же намного меньше пути, который он преодолел вместе с поездом относительно Земли. Следовательно, при механическом движении относительным является и путь.
Любое движение, как и покой тела (как частный случай движения) относительны. Для ответа на вопрос, покоится тело или движется и как именно движется, необходимо указать, относительно каких тел рассматривается движение этого тела. В противном случае никакое высказывание о его движении не может иметь смысла.
Тела, относительно которых рассматривается данное движение, называют системой отсчета. Выбор системы отсчета зависит от условий задачи, тогда положение одного и того же тела можно одновременно рассматривать в разных системах координат. Следовательно, относительно разных тел отсчета в разных системах координат у одного и того же тела могут быть совершенно различные координаты. Это значит, что положение тела относительно: оно различно относительно разных тел отсчета и связанных с ними разных систем координат.
Но относительно не только положение тела. Относительно и его движение. В чем же относительность движения? Например, пилоту необходимо знать движение самолета относительно Земли и относительно воздуха, который в ненастную погоду сам движется; артиллеристу важно знать движение снаряда не только относительно Земли, на которой стоит орудие, но и относительно танка, в который он должен произвести выстрел, и который сам движется относительно Земли и т. д.
Движения одного и того же тела относительно разных тел отсчета, движущихся относительно друг друга, могут довольно сильно отличаться.
Что такое относительность движения
Содержание статьи
В чем состоит относительность движения
Если в спокойную погоду проснувшийся в каюте парусной яхты пассажир выглянет в иллюминатор, он далеко не сразу сообразит – плывет корабль или лежит в дрейфе. За толстым стеклом однообразная морская гладь, выше – небесная синь с неподвижными облачками. Однако, в любом случае яхта будет находиться в движении. И больше того – сразу в нескольких движениях по отношению к разным системам отсчета. Даже не беря во внимание космические масштабы, этот человек, находясь в состоянии покоя относительно корпуса яхты, оказывается в состоянии движения относительно окружающей его массы воды. Это можно увидеть по кильватерной струе. Но и в случае, если яхта дрейфует со спущенным парусом, она движется с водным потоком, образующим морское течение.
Таким образом, любое тело, находящееся в состоянии покоя относительно одного тела (системы отсчета), одновременно находится в состоянии движения относительно другого тела (другой системы отсчета).
Принцип относительности Галилея
Об относительности движения задумывались уже средневековые ученые, и в эпоху Возрождения эти идеи получили свое дальнейшее развитие. «Почему мы не ощущаем вращения Земли?» – задавались вопросом мыслители. Четкую формулировку на основе физических законов принципу относительности придал Галилео Галилей. «Для предметов, захваченных равномерным движением, – вывел ученый, – это последнее как бы не существует и проявляет свое действие только на вещах, не принимающих в нем участия». Правда, это утверждение действительно только в рамках законов классической механики.
Относительность пути, траектории и скорости
Пройденный путь, траектория и скорость тела или точки будут также относительны в зависимости от выбранной системы отсчета. Возьмите пример с идущим через вагоны человеком. Его путь за определенный промежуток времени относительно состава будет равен пройденному им собственными ногами расстоянию. Путь же относительно земли будет складываться из расстояния, которое проехал поезд, и непосредственно пройденного человеком расстояния, причем, независимо от того, в какую сторону он шел. То же со скоростью. Но здесь скорость движения человека относительно земли будет выше скорости движения поезда – если человек идет по движению поезда, и ниже – если он идет в обратную движению сторону.
Относительность траектории точки удобно проследить на примере гаечки, закрепленной на ободе велосипедного колеса и удерживающей спицу. Относительно обода она будет неподвижна. Относительно корпуса велосипеда – это будет траектория окружности. А относительно земли траектория этой точки будет представлять непрерывную собой цепь полуокружностей.
Относительность механического движения
теория по физике 🧲 кинематика
Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.
Относительность перемещения
Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.
Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.
Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:
Относительность скорости в ПСО и НСО
Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.
Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.
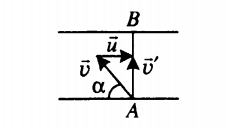
Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.
Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:
Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):
Косинусу 0,5 соответствует угол, равный 60 градусам.
Относительная скорость двух тел
Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.
Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:
v отн — относительная скорость, или скорость первого тела относительно второго, v 1 и v 2 — скорость первого и второго тела относительно СО.
Варианты обозначения относительной скорости и их проекций:
Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.
Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.
Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:
Скорость второго автомобиля относительно дороги равна 80 км/час.
Правила сложения векторов
| Сложение двух сонаправленных векторов | |
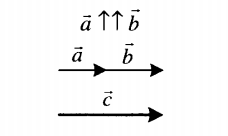 | Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону. Его длина равна сумме длин слагаемых векторов: c = a + b. |
| Сложение двух противоположно направленных векторов | |
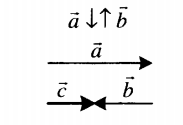 | Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|. |
| Сложение двух векторов, расположенных друг к другу под углом | |
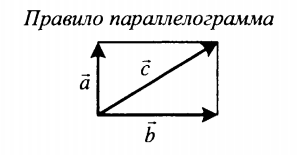
| Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов. | |
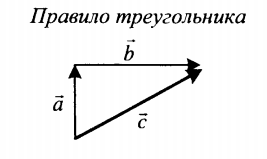 | Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: 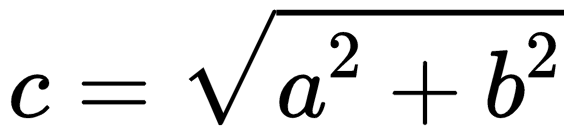 . . |
 | |
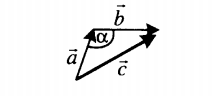 | Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов: 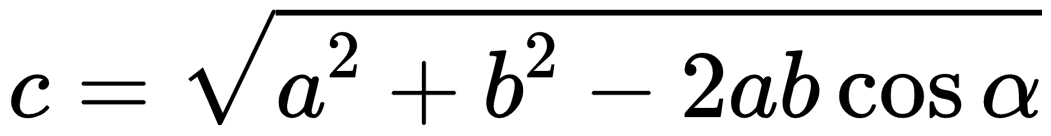 . . |
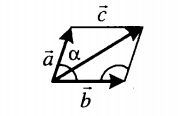 | Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: 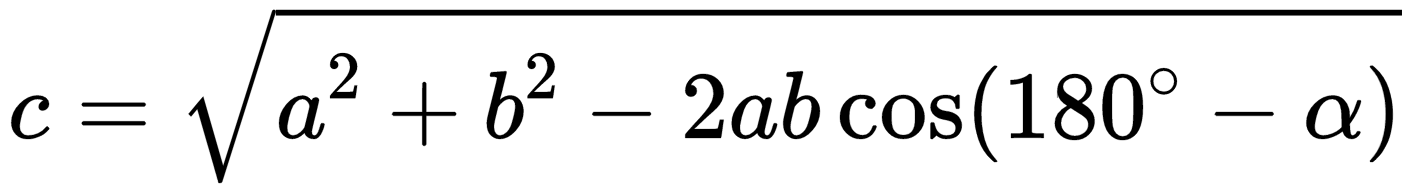 . . |
Правила вычитания векторов
Эта таблица иллюстрирует правила вычитания векторов на примере векторов 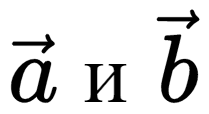
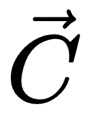
Алгоритм решения
Решение
Записываем данные относительно Земли:
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость второго автомобиля относительно оси ОХ ( v 2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v 1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость автомобиля относительно земли ( v 1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v 2). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50
pазбирался: Алиса Никитина | обсудить разбор | оценить