в чем состоит физический смысл уравнения бернулли
В чем состоит физический смысл уравнения бернулли
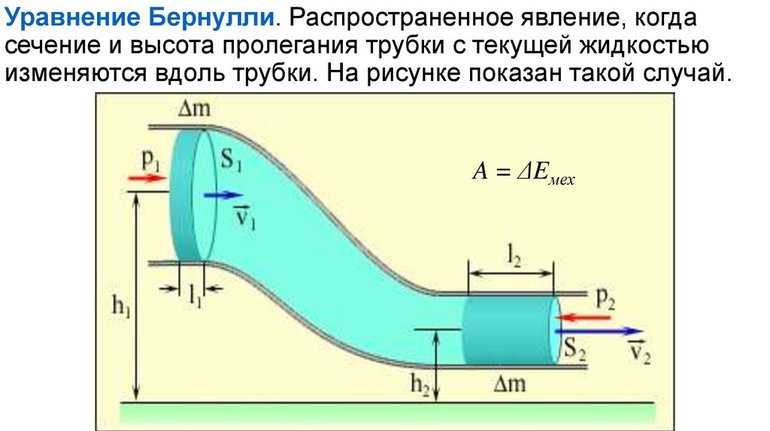
Уравнение Бернулли для реальной и идеальной жидкости
Уравнение Бернулли позволяет выполнить расчет водоснабжения и отопления: Подобрать диаметры и насосы. В этой статье будет расписан энергетический и геометрический смысл уравнения Бернулли.
График Бернулли и уравнение Бернулли для идеальной жидкости:
График Бернулли и уравнение Бернулли для реальной жидкости:
Смысл уравнения Бернулли
Смысл уравнения Бернули в том, чтобы показать, что внутри системы заполненной жидкостью (участка трубопровода) сохраняется общая энергия между разными точками. То есть на участке трубопровода необходимо выделить две точки, и эти две точки равны друг другу по значению полной энергии. Полная энергия состоит из потенциальной и кинетической энергии.
Назначение уравнения Бернули
Понять, как распределяется давление в системе трубопроводов. А также с помощью уравнения находить неизвестные параметры внутри системы. Например, найти давление в каждой течке пространства системы заполненной жидкостью.
Подробнее на видео: (для запуска видео кликните по окошку) На видео намного больше информации
Задача. Пример решения уравнения Бернулли
По решению задачи необходимо найти давление в точке 2 при известных параметрах: давление и расход.
Как понять уравнение Бернулли?
Для расчета уравнения Бернулли необходимо выбрать две точки в пространстве
Точка 1 – это место где известно давление
Точка 2 – это место где нужно узнать давление
Поймите, что каждый кусок формулы измеряется давлением: м.в.ст. (метр водяного столба)
То есть для того, чтобы быстро считать гидравлику систем водоснабжения и отопления, необходимо меньше всего выражаться в Барах, Паскалях и тому подобное.
Проще выражать давление в единице измерения: м.в.ст. (метр водяного столба)
Вы этим самым упростите себе жизнь… просто другая единица это еще один процесс, который отнимает время.
Сборка формулы уравнения Бернулли
Как избавится от минуса?
Как избавится от множителя (-1)?
Что такое идеальная жидкость?
Формула Бернулли для реальной жидкости
Коэффициент Кориолиса – это поправка кинетической энергии на реальную жидкость.
Потому что реальная жидкость движется не равномерно
У реальной жидкости серединная струйка воды движется быстрее остальных. При ламинарном режиме градиент: Чем ближе к стенке, тем медленнее движется поток воды.
Формула коэффициента Кориолиса
Что такое коэффициент Кориолиса?
Коэффициент Кориолиса характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока.
Чему равен коэффициент Кориолиса?
Нд.п. – Это динамические потери. Это потери вызванные движением воды.
Имеются дополнительные задачи с уравнением Бернули на реальную жидкость:
Посмотрите видеоурок по составлению уравнения Бернулли:
Как сделать гидравлический расчет погружного насоса?
Формулировка закона Бернулли и его математическое выражение
Обновлено: 02 Июня 2021
Принцип Бернулли заложил основы знания о движении жидкости, которое впоследствии перешло в самостоятельную науку — гидродинамику.
Физическая сущность закона Бернулли
Швейцарский математик и физик Даниил Бернулли родился в 1716 году в Голландии. За свою научную карьеру он получил звания Почетного члена Берлинской, Петербургской и Парижской академии наук, являлся членом Лондонского королевского общества. Главным научным трудом ученого является работа «Гидродинамика, или изъяснение сил и движений жидкости», опубликованная в 1733 году. Именно в этой книге были описаны физические основы механики жидкости.
Закон, названный его именем, Бернулли сформулировал во время работы в России, изучая взаимосвязь давления жидкости с ее скоростью. В математическом выражении он определяется уравнением Бернулли. Давайте разберемся, в чем состоит сущность закона.
Для начала определим, что закон Бернулли рассматривает движение потока несжимаемой идеальной жидкости, на которую действуют только силы тяжести и силы упругости.
Идеальная жидкость — это жидкость, в которой полностью отсутствует внутреннее трение и теплопроводность, ввиду чего, она лишена касательных напряжений между соседними слоями.
Подобная идеализация применяется при рассмотрении течения в гидродинамике. В законе Бернулли рассматривается стационарное течение жидкости — это движение слоев жидкости относительно друг друга и относительно ее самой, при котором скорость потока в некой конкретной точке не меняется, сохраняя свое постоянное значение. Давление при стационарном течении идеальной жидкости одинаково во всех поперечных сечениях трубки тока.
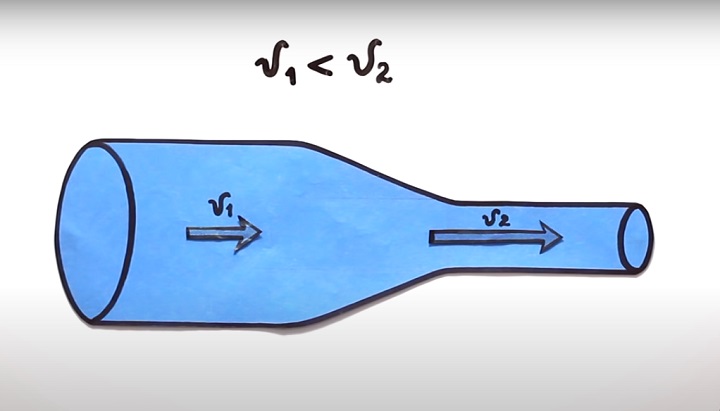
Для наглядности рассмотрим стационарное течение идеальной жидкости по трубе переменного сечения. В одном месте сечение этой трубки равно S1, а в другом — S2. При стационарном потоке через все сечения за определенный промежуток времени пройдет одинаковый объем жидкости, так как в ином случае, невозможность сжатия привела бы к ее разрыву. Таким образом, мы получаем уравнение неразрывности струи, определяющее соотношение между скоростью течения (v) и площадью сечения (S): S1v1=S2v2
При этом скорость давление в сечении S1 меньше, чем в сечении S2. Как вы думаете, в каком из сечений скорость течения жидкости будет больше? Казалось бы, что по логике, скорость должна увеличиваться в том месте, где больше давление. Однако, согласно закону Бернулли, скорость увеличивается с уменьшением площади сечения. В этом-то и состоит парадоксальность принципа.
Закон Бернулли гласит, в тех участках течения жидкости или газа, где скорость больше, давление меньше, и наоборот, с увеличением давления жидкости, протекающей в трубе, скорость ее движения уменьшается. То есть, где больше скорость (v), там меньше давление (p).
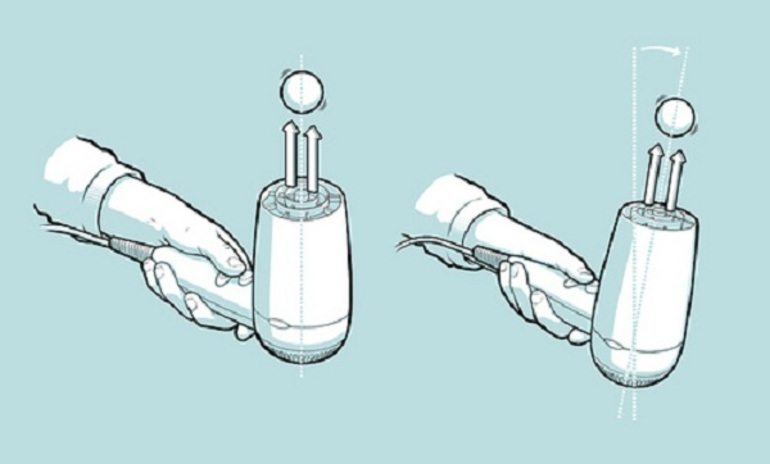
Чтобы убедиться в этом, достаточно провести небольшой опыт из подручных средств. Возьмите два шара одного размера и подвесьте их так, чтобы между ними сохранялось небольшое расстояние. Подуйте между шарами или пустите воздух из фена. Шары вместо того, чтобы отдалиться, притянутся друг к другу. Это прямое следствие описанного закона, так как в том месте, куда вы дули, давление стало уменьшаться, а скорость шаров возросла, приблизив их друг к другу.
Закон Бернулли как следствие закона сохранения энергии
Из уравнения неразрывности следует, что в идеальной жидкости сумма статистического и динамического давлений и скоростного напора постоянна в любом сечении вдоль трубы. Являясь следствием закона сохранения, вывод уравнение Бернулли для элементарной струйки жидкости выглядит так:
\rho\) — плотность жидкости, \(
v\) — скорость потока, \(
h\) — высота, на которой находится рассматриваемый элемент жидкости, \(
p\) — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости, \(
g\) — ускорение свободного падения.
При этом давление P — это статическое давление, которое получается в результате взаимодействия соседних слоев жидкости. Величина ρv2/2 — это динамическое давление, обусловленное движением жидкости, а ρgh — это давление, образованное массой вертикального столба жидкости высотой h, создаваемое силой тяжести.
Все эти величины имеют специальные обозначения, где h — высота положения или геометрический напор, P / ρ∙g — пьезометрический напор, v2 / 2g — скоростной напор.
Сумма трех слагаемых уравнения называется полным напором (H), то есть для идеальной жидкости при стационарном течении сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная вдоль струйки.
Для трубы, расположенной горизонтально, где величина высоты остается неизменной, уравнение Бернулли упрощается и выглядит так:
Проявление закона Бернулли в жизни
Закон Бернулли описывает одно из основных свойств гидравлики. Эффект, описанный швейцарским ученым, широко проявляется в природе и быту. Также широко его применение в технике. На основе принципа Бернулли работают такие приборы, как пульверизатор, водоструйный насос, аэрограф.
Чтобы понять механизм устройства, рассмотрим строение пульверизатора, которое включает в себя вертикальную трубку и горизонтальное сопло. Вертикальную трубку опускают в жидкость, в то время как по соплу пропускают воздух. Атмосферное давление, которое больше давления в струе воздуха, заставляет жидкость подниматься по трубке. Следовательно, при попадании в струю воздуха, происходит распределение жидкости.
В повседневной жизни закон Бернулли можно наблюдать, сидя у камина. При сильном ветре скорость воздушного потока возрастает, и, соответственно, падает давление. И так как давление воздуха в комнате выше, пламя, уходит вверх по дымоходу.
Это свойство используется и в аэродинамике для объяснения того, как возникает подъемная сила самолета или другого летательного аппарата, которое тяжелее воздуха.
В истории имеются и случаи отрицательного проявления закона. В 1912 году произошло столкновение океанского парохода «Олимпик» с гораздо меньшим по масштабам крейсером «Гаук», который плыл параллельно пароходу на расстоянии около 100 метров. Вдруг «Гаук» резко двинулся прямо на «Олимпик» и протаранил его силой удара. Так как два корабля были друг к другу слишком близко, скорость воды между ними стала больше, чем с другой стороны, вызвав дополнительную силу. Следовательно, вместо того, чтобы отдалиться, корабли притянулись друг к другу, что и стало причиной катастрофы.
В природе закон Бернулли проявляется во время урагана, когда из-за сильного ветра с домов слетают крыши. Это происходит, потому что скорость, с которой движется воздух вверху, очень большая, тогда как на чердаке она равна нулю. Как вы уже узнаете, там, где скорость потока больше, давление меньше, а там, где скорость меньше, давление больше. В результате образовавшейся разности давлений ураган и срывает кровлю.
Существует еще большое количество интересных примеров, изучение которых во многом упрощает усвоение закона Бернулли. Если вам нужно определить проявление закона в каком-то конкретном явление, обращайтесь к специалистам сервиса Феникс.Хелп, которые помогут решить задачу любой сложности.
Уравнение Бернулли
Уравнение Бернулли для потока идеальной жидкости
Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении.
Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.
Уравнение Бернулли можно записать и в другом виде, умножим обе части уравнения на g получим:
Физический смысл уравнения Бернулли
Составляющие уравнения Бернулли являются различными формами удельной (отнесенной к единице массы) механической энергии жидкости:
Физический и энергетический смысл уравнения Бернулли заключается в постоянстве полной удельной энергии вдоль элементарной струйки идеальной жидкости.
Уравнение Бернулли отражает закон сохранения механической энергии для идеальной несжимаемой жидкости.
Уравнение Бернулли для потока реальной вязкой жидкости
Если на участке между расчетными сечениями не совершается механическая работа, а движение является установившимся, без притока и отбора жидкости, и сама жидкость является несжимаемой, то для потока будут справедливы зависимости:
Иллюстрация уравнения Бернулли
Для иллюстрации закона Бернулли на координатной плоскости, совмещенной с принципиальной гидравлической схемой системы изображают напорную и пьезометрическую линии.
Уравнение Бернулли для горизонтальной трубы
Для горизонтальных трубопроводов и силовых гидроприоводов, в которых пьезометрический набор существенно превышает геометрический удобна следующая форма записи уравнения Бернулли:
Алгоритм решения задач с помощью уравнения Бернулли
Задачи с помощью уровнения Бернулли удобно решать в следующей последовательности:
Исследования учёного
Даниил Бернулли родился в Голландии в 1700 году. В 1725 году он начал работать на кафедре физиологии, где увлёкся основами теоретической физики. Через 25 лет он возглавил кафедру экспериментальной физики, которой и руководил до конца своих дней. Основным его трудом считается создание теории гидродинамической зависимости, известной как Закон Бернулли. Открытие учёного предвосхитило зарождение молекулярно-кинетического учения поведения газов.
Причиной открытия принципа стало изучение действия закона сохранения энергии в различных ситуациях. Бернулли установил, что давление жидкости в замкнутом пространстве зависит от сечения объекта, в котором она находится. Чем меньше сечение трубы, тем ниже будет созданное давление в пропускаемом через неё жидком веществе.
Этот факт был доказан экспериментально и описан математически.
Правило в математической формулировке имеет вид (pv 2 / 2) + p * g * h + ρ = const, где:
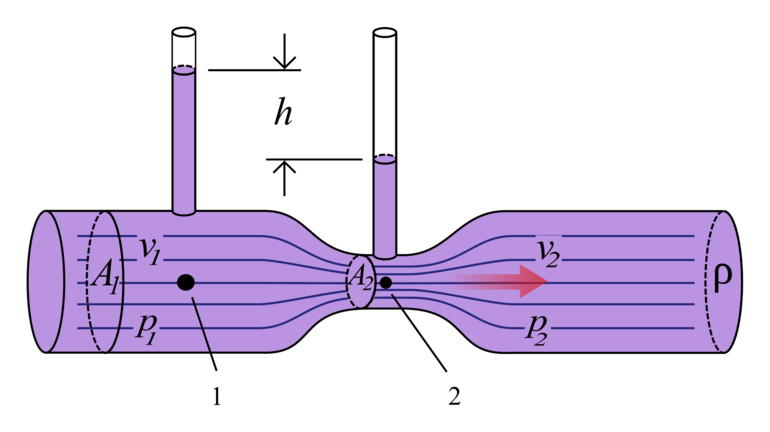
Чтобы понять физический смысл уравнения Бернулли, нужно рассмотреть трубу переменного сечения, в которой существует точка А и Б. Первая располагается в широкой части, а вторая — в узкой. В соответствии с уравнением непрерывности скорость V1 в части трубы, имеющей большее сечение, будет меньше, чем скорость жидкости V2 в узком сечении. Если в жидкость поместить прибор для измерения давления, он покажет какое-то значение P1 в точке A и P2 в точке Б. При этом там, где скорость движения жидкости медленнее, давление будет больше.
Объясняется это следующим образом: если V1 больше V2, значит, при движении происходит изменение скорости течения. Представив, что в жидкости находится точка, можно утверждать о её движении с ускорением. Это означает, что на неё действуют силы.
Одна из них совпадает с направлением течения, тем самым ускоряя движение. Обусловлена эта сила разностью давления.
Так как движение происходит от точки А к Б, то и давление возле А будет больше, чем около Б. Эта разность давлений и приводит к ускорению.
Условия действия
Закон применим для условия, при котором соблюдается неразрывность струи воздуха или жидкости. В тех участках потока, где скорость течения больше, давление будет меньше и наоборот. Это утверждение и называется теоремой Бернулли. По сути, закон позволяет установить связь между давлением, скоростью, высотой.
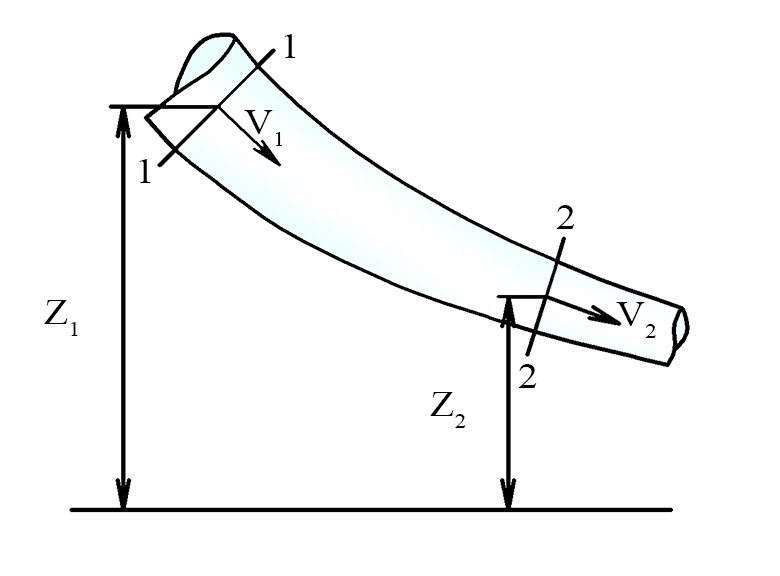
Пусть имеется труба переменного сечения с изменяющейся высотой. Внизу она широкая, а затем сужается. По ней течёт жидкость. Площадь сечения можно обозначить как S1 и S2, а давление участков и скорость движения на них P1, P2, V1, V2. Высота внизу будет равняться S1, а вверху S2.
Выделив участок в трубе с жидкостью, можно сказать, что она движется слева направо и через некоторое время полностью сдвинется в область S2. Изменение положения слева будет равно расстоянию дельта L1, а справа — дельта L2.
Течение является:
Последнее обозначает, что нет вязкости. Поэтому на жидкость действует только сила упругости и тяжести, а силы трения нет. Система не является замкнутой, а значит закон сохранения энергии применительно к рассматриваемому участку использовать нельзя. Зато вполне можно применить теорему о кинетической энергии.
Для газов уравнение можно использовать лишь в том случае, если их плотность изменяется незначительно. Но касаемо аэродинамики учитывается и то, что изменение давления воздуха гораздо меньше атмосферного. Поэтому уравнение можно применять в аэродинамических расчётах.
Согласно ему, сумма действующих всех сил на тело (рассматриваемый кусок жидкости) равняется изменению кинетической энергии объекта: ΣAi = ΔEk. На нижний участок действует сила давления, выполняющая положительную работу, а на верхний — отрицательную. Кроме этого, действует и сила тяжести. Так как жидкость поднимается, она имеет тоже отрицательный знак. Сила бокового давления перпендикулярна любой точке в системе, поэтому никакого влияния она не оказывает.
Количественная сторона
Исходя из сил, действующих на тело, изменение кинетической энергии можно описать выражением: ΔEk = Ap1 +Ap2 +Ag. Чтобы найти работу, необходимо силу умножить на пройденное расстояние. Поэтому работа силы давления равна произведению самой силы F на модуль перемещения ΔL и косинусу угла между ними: Ap1 = F1* ΔL *1.
Зная количественные показатели всех трёх работ, можно найти изменение кинетической энергии. Из физики известно, что оно равно разнице конечной и начальной энергии. Течение стационарное, значит, скорость с течением времени не изменится. Следовательно, кинетическая энергия будет определяться разницей появившейся энергии в верхней части и ушедшей из нижней области: ΔEk = (m2 * v2 2 )/2 — (m1 * v1 2 ) / 2.
То место, где давление p1, некая точка внутри трубки, пусть будет обозначено цифрой один, а там, где p2, — цифрой два. Всё что относится к единице можно записать в левой части, а к двойке — в правой: ρ1 * g * h1 + (ρ * v1 2 ) / 2 = ρ * g * h2 + (ρ * v2 2 ) / 2. Полученная формула показывает, что при переходе в пределе одной линии скорость, давление и высота изменяются. Поэтому в любой точке будет справедливым выражение: ρ1+ ρ * g * h + (ρ * v1) / 2 = const. Это и есть количественное описание уравнения Бернулли для идеальной жидкости.
Применение в гидравлике
Наиболее типичным примером использования уравнения является решение заданий по нахождению скорости вытекания жидкости из отверстия в широком сосуде. Такой ёмкостью называют систему, в которой диаметр сосуда значительно больше размера отверстия. Необходимо найти скорость вытекающей жидкости U1. Известно, что высота столба жидкости, на который действует сила тяжести g, равна h.
Пусть в жидкости, находящейся сверху, имеется точка один. Через некоторое время она окажется внизу в положении два. На верх жидкости давит атмосферное давление, поэтому p1=pатм. Высота в точке один равна h. Скорость U1 считают равной нулю. Давление p2 в точке два будет также равно атмосферному. Так как жидкость опустится на дно, то высота h2 станет нулевой.
Интересным фактом является то, что полученный ответ при решении задачи называется формулой Торричелли. Она показывает, что скорость, с которой вытекает жидкость из широкого сосуда, равна скорости тела при свободном падении с той же высоты.
Используя уравнение, можно легко рассчитать давление жидкости на дно и стенки сосуда. В этом случае закон Бернулли является обобщением для формулы гидростатического давления. Пусть имеется сосуд с жидкостью высотой h. Точка, находящаяся наверху, характеризуется давлением p1 = pатм., высотой h1 равной h и скоростью U1. Для точки на дне параметры будут следующие: p2 = p, h2 = 0, U2 = 0. Скорости принимаются равными нулевому значению, так как рассматриваемая жидкость находится в состоянии покоя.
Данные следует подставить в уравнение. В итоге получится равенство: pатм + ρ * g * h + 0 = p + 0 + 0. Из него несложно найти неизвестное: p = pатм + ρ * g * h. Полученный ответ является формулой гидростатического давления и подтверждает закон Паскаля.
Аналогично уравнение Бернулли для потока реальной жидкости используется при расчёте расхода в карбюраторе, пульверизаторе, учёте статического и динамического давления.
Подъёмная сила
Самолёт летает благодаря тому, что набегающий на крыло напор воздуха создаёт подъёмную силу. Её можно рассчитать и оценить с помощью уравнения. Геометрически крыло можно представить в виде плоскости с углом a (угол атаки). На него действует поток воздуха со скоростью U. Частица воздуха ударяет в твёрдую поверхность и отражается от неё. Угол отражения равен углу атаки, а её скорость равняется U’. Нужно рассчитать подъёмную силу. Для этого необходимо выполнить три шага:
В результате получится, что на крыло действует сила, состоящая из двух компонентов: подъёмной силы Fy и аэродинамического сопротивления Fx. Fy = Cy * p * U 2 * S, а Fx = Cx * p * U 2 * S. В формулах С является коэффициентом, а S — площадью крыла.
Для расчёта используется уравнение Бернулли. Выглядеть оно будет следующим образом: Pп. к + (ρ * Uп. к) * 2 / 2 + ρ * g * hп. к = Pн. к + (ρ * Uн. к) * 2 / 2 + ρ * g * hн. к, где: п. к — под крылом, а н. к — над крылом. Это уравнение можно упростить, приняв, что давления над и под крылом примерно одинаковые, поэтому плотность будет также одинаковая. Кроме того, высота крыла довольно маленькая. Исходя из этого, формулу можно упростить, и она примет вид: pп. к-pн.к = (ρ * (Uн.к + Uп. к) * (Uн.к — Uп. к)) / 2 = 2 * U1 * U2. Теперь можно найти подъёмную силу. Для этого разность давлений нужно умножить на площадь крыла: Fy = (pп.к-pн. к) * S.
Таким образом, используя метод, можно рассчитать подъёмную силу, обусловленную эффектом Бернулли. Например, пусть дано, что площадь крыла равна 50 м². Скорость потока воздуха над крылом и под ним соответственно равны: U1 = 320 м/с, U2 = 290 м/с. Найти грузоподъёмность. Для решения задания нужно знать дифференциальную плотность воздуха. Это справочная величина, равная 1,29 кг/м3.
Используя уравнение Бернулли, можно записать: pп. к-pн.к = ρ * (U2н.к — U2п. к). Подъёмная сила равна площади крыла, умноженной на разность давления. Подставив одно выражение в другое, получим рабочую формулу: Fy = ρ * (U2н.к — U2п. к) * S / 2. После выполнения расчёта получится ответ 590 кН. То есть грузоподъёмность самолёта составит порядка 59 тонн.
Реальные вычисления для таких задач довольно сложные, поэтому часто используют онлайн-калькуляторы.