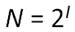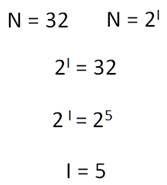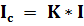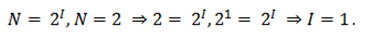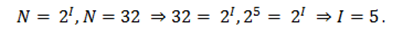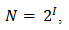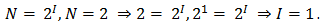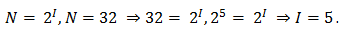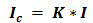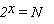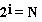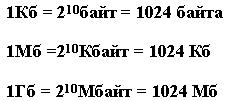в чем состоит алфавитный подход к оценке количества информации
Алфавитный подход к определению количества информации
Урок 6. Информатика 8 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Алфавитный подход к определению количества информации»
Содержательный подход к измерению информации рассматривает информацию с точки зрения человека, как уменьшение неопределенности наших знаний.
Однако любое техническое устройство не воспринимает содержание информации. Поэтому в вычислительной технике используется другой подход к определению количества информации. Он называется алфавитным подходом.
При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
Проще всего разобраться в этом на примере текста, написанного на каком-нибудь языке. Для нас удобнее, чтобы это был русский язык.
Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами.
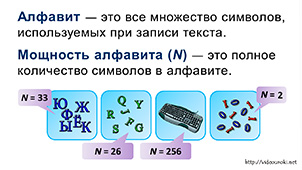
Алфавит — это множество символов, используемых при записи текста.
Мощность (размер) алфавита — это полное количество символов в алфавите.
Мощность алфавита обозначается буквой N.
· мощность алфавита из русских букв равна 33;
· мощность алфавита текста набранного с клавиатуры равна 256 (строчные и прописные латинские и русские буквы, цифры, знаки арифметических операций, скобки, знаки препинания и т.д.);
· мощность двоичного алфавита равна 2.
При алфавитном подходе считается, что каждый символ текста имеет информационную емкость. Информационная емкость знака зависит от мощности алфавита.
Алфавит, с помощью которого записано сообщение состоит из N знаков. В простейшем случае, когда длина кода сообщения составляет один знак, отправитель может послать одно из N возможных сообщений, которое будет нести количество информации I.
Тогда, из формулы можно определить количество информации, которое несет знак в двоичной знаковой системе
.
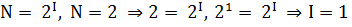
Информационная емкость знака двоичной знаковой системы составляет 1 бит.
Определите, какое количество информации несет буква русского алфавита (без буквы ё).
Буква русского алфавита несет 5 битов информации.
Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.
Количество информации в сообщении можно посчитать, умножив количество информации, которое несет один знак на количество знаков в сообщении.
где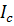 
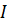
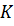
— количество информации в сообщении,
— количество информации, которое несет один знак,
— количество знаков в сообщении.
Какое количество информации содержит слово «ПРИВЕТ», если считать, что алфавит состоит из 32 букв?
Количество знаков в сообщении равно 6, а мощность данного алфавита равна 32.
Что нам нужно найти? Нам нужно найти какое количество информации содержит слово «ПРИВЕТ».
Посмотрим на наше сообщение, оно содержит несколько знаков, значит для того чтобы найти количество информации нашего сообщения, нам нужно умножив количество информации, которое несет один знак, на количество знаков в сообщении, т.е. воспользоваться формулой «и» суммарное равно «и» умножить на «к».
Но мы еще не можем воспользоваться формулой, т.к. не знаем какое количество информации несет один знак. Для этого воспользуемся формулой Хартли. Сообщение записано с помощью алфавита, мощность которого равна 32, т.е. N равно 32. Мы получили уравнение. Решив это уравнение, мы получили, что количество информации, которое несет один знак нашего алфавита, равно 5 бит. Зная количество информации, которое несет один знак нашего алфавита, и количество знаков в сообщении, мы можем найти, какое количество информации содержит наше сообщение.
Алфавитный подход к оценке количества информации. Формула Хартли
Вы будете перенаправлены на Автор24
Содержательный подход к оценке количества информации, который мы рассматривали ранее, измеряет ее количество, как уменьшение неопределенности наших знаний.
Однако любое техническое устройство не способно воспринимать непосредственно содержание информации, оно лишь понимает наличие или отсутствие электрических сигналов. Вследствие чего в вычислительной технике вынуждены использовать другой подход к оценке количества информации, который называется алфавитным.
Принцип алфавитного подхода к оценке количества информации
Алфавитный подход строится на принципе, утверждающем, что любое сообщение можно представить в виде кодов с помощью конечной последовательности символов, содержащейся в любом алфавите. Носители информации содержат любые последовательности символов, которые могут храниться, передаваться и обрабатываться как с помощью человека, так и с помощью технических устройств, в частности компьютера. Этот подход описал А.Н. Колмогоров, согласно которому, информативность, заключающаяся в последовательности символов, не может зависеть от содержания самого сообщения, а может определяться лишь минимальным количеством символов, необходимых для ее кодирования. Подобный подход к оценке количества информации носит объективный характер, так как не зависит от получателя, принимающего сообщения. Смысл же сообщений может учитываться только на этапе выбора алфавита кодирования либо не учитываться совсем.
В основу принципа этого подхода лег подсчет числа символов в сообщении, таким образом, важна только длина сообщения и совсем не учитывается его содержание. Однако на длину сообщения может влиять мощность алфавита используемого языка.
Мощность алфавита и информационная емкость. Формула Хартли
Все множество символов, из которых состоит язык, можно традиционно назвать алфавитом. Как правило, под алфавитом понимаются только буквы, но кроме них при написании текстов используются знаки препинания, цифры, скобки, пробелы, их тоже, в свою очередь, можно включить в алфавит.
Например:
Готовые работы на аналогичную тему
При алфавитном подходе считают, что каждый символ текста несет в себе определенную информационную емкость, которая, в свою очередь, зависит от мощности алфавита.
Хартли утверждал, что на количество информации, содержащейся в сообщении, может влиять фактор неожиданности, который, в свою очередь, зависит от вероятности получения сообщения. Если эта вероятность получения сообщения высокая, а неожиданность при этом низкая, то сообщение будет содержать мало полезной для человека информации.
Однако при создании своей формулы Р.Хартли полностью исключил фактор неожиданности. Формула Хартли работает только в том случае, когда появление символов равновероятно и они статистически независимы.
Например, с помощью приведенной формулы можно определить количество информации, которое несет знак в двоичной системе счисления:
Информационная емкость знака двоичной системы составляет 1 бит.
Необходимо определить информационную емкость буквы русского алфавита (без учета буквы «ё»).
Решение:
Представим себе, что текст к нам поступает последовательно, по одному знаку, словно бумажная лента, выползающая из телеграфного аппарата. Предположим, что каждый символ, который появляется на ленте, с равной вероятностью может быть любым символом алфавита. В действительности это не совсем так, но для упрощения примем такое предположение.
Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.
Количество информации в сообщении можно определить, используя формулу:
Рассмотрим пример решения задачи
Решение. Чтобы решить задачу, для начала определим количество знаков в сообщении и мощность используемого алфавита.
Необходимо определить какое количество информации содержит слово «Привет».
Однако мы не сможем воспользоваться этой формулой, поскольку нам не известно какое количество информации несет один знак ($I$).
Единицы измерения информации
Проведем несложный расчет и получим, что страница содержит:
$50 \cdot 60 = 3000$ байт информации.
Объем же информации, содержащейся в книге:
$3000 \cdot 50 = 150 \ 000$ байт.
Любая система единиц измерения содержит основные единицы и производные от них.
При измерении больших объемов информации на практике широко используются следующие производные от байта единицы, которые приведены в таблице:
Алфавитный подход к определению количества информации
Цели урока:
1) Обучающая: рассмотреть алфавитный подход к измерению количества информации, научиться вычислять количество информации с точки зрения алфавитного подхода.
2) Развивающая: развитие у учащихся самостоятельности и познавательной активности.
3) Воспитывающая: воспитывать дисциплинированность, аккуратность, собранность.
Литература:
1) Угринович Н. Д. «Информатика 8 класс»,
2) Заславская О. Ю., Левченко И. В. «Информатика: весь курс».
1) Угринович Н. Д. «Информатика 8 класс».
Тип урока: ознакомление с новым материалом
План урока:
1. Организационный этап.
2. Актуализация знаний.
3. Подготовка учащихся к усвоению нового материала.
4. Этап получения новых знаний.
5. Этап обобщения и закрепления нового материала.
7. Заключительный этап.
Ход урока
1. Организационный этап.
Здравствуйте. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.
2. Актуализация знаний.
1) В чём заключается содержательный подход к измерению информации? (Количество информации — мера уменьшения неопределённости знаний при получении информационных сообщений.)
2) Какую минимальную единицу информации используют для измерения количества информации? (Бит)
3) Какую формулу используют для определения количества информации? (Формулу Хартли)
4) Производится бросание симметричной четырехгранной пирамидки. Какое количество информации мы получаем в зрительном сообщении о ее падении на одну из граней? (2 бита)
6) Из непрозрачного мешочка вынимают шарики с номерами и известно, что информационное сообщение о номере шарика несет 5 битов информации. Определите количество шариков в мешочке. (35)
3. Этап получения новых знаний.
Скачать видеоурок «Алфавитный подход к определению количества информации»
Содержательный подход к измерению информации рассматривает информацию с точки зрения человека, как уменьшение неопределенности наших знаний.
Однако любое техническое устройство не воспринимает содержание информации. Поэтому в вычислительной технике используется другой подход к определению количества информации. Он называется алфавитным подходом.
При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
Проще всего разобраться в этом на примере текста, написанного на каком-нибудь языке. Для нас удобнее, чтобы это был русский язык.
Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, пропуск между словами.
Алфавит — это множество символов, используемых при записи текста.
Мощность (размер) алфавита — это полное количество символов в алфавите.
Мощность алфавита обозначается буквой N.
· мощность алфавита из русских букв равна 33;
· мощность алфавита из латинских букв — 26;
· мощность алфавита текста набранного с клавиатуры равна 256 (строчные и прописные латинские и русские буквы, цифры, знаки арифметических операций, скобки, знаки препинания );
· мощность двоичного алфавита равна 2.
При алфавитном подходе считается, что каждый символ текста имеет информационную емкость. Информационная емкость знака зависит от мощности алфавита.
Алфавит, с помощью которого записано сообщение состоит из N знаков. В простейшем случае, когда длина кода сообщения составляет один знак, отправитель может послать одно из N возможных сообщений, которое будет нести количество информации I.
N — количество знаков в алфавите знаковой системы, I — количество информации, которое несет каждый знак.
Например, из формулы можно определить количество информации, которое несет знак в двоичной знаковой системе
Информационная емкость знака двоичной знаковой системы составляет 1 бит.
Задача 1. Определите, какое количество информации несет буква русского алфавита (без буквы ё).
Буква русского алфавита несет 5 битов информации.
Формула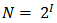 
связывает между собой количество возможных событий и количество информации, которое несёт полученное сообщение. В рассматриваемой ситуации N — это количество знаков в алфавите, знаковой системы, а I — количество информации, которое несёт один знак.
Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.
Количество информации в сообщении можно посчитать, умножив количество информации, которое несет один знак на количество знаков в сообщении.
где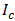 
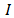
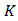
— количество информации в сообщении
— количество информации, которое несет один знак
— количество знаков в сообщении
Давайте решим с вами задачу.
Задача 2. Какое количество информации содержит слово «ПРИВЕТ», если считать, что алфавит состоит из 32 букв?
Решение. Что нам требуется найти в данной задаче? Нам нужно найти какое количество информации содержит слово «ПРИВЕТ».
Что нам для этого дано?
Дано: количество знаков в сообщение и мощность алфавита.
Количество знаков в сообщении равно 6, а мощность данного алфавита равна 32.
Что нам нужно найти? Нам нужно найти какое количество информации содержит слово «ПРИВЕТ».
Посмотрим на наше сообщение, оно содержит несколько знаков, значит для того чтобы найти количество информации нашего сообщения, нам нужно умножив количество информации, которое несет один знак, на количество знаков в сообщении, воспользоваться формулой «и» суммарное равно «и» умножить на «к».
Но мы еще не можем воспользоваться формулой, т.к. не знаем какое количество информации несет один знак. Для этого воспользуемся формулой Хартли. Сообщение записано с помощью алфавита, мощность которого равна 32, N равно 32. Мы получили уравнение. Решив это уравнение, мы получили, что количество информации, которое несет один знак нашего алфавита, равно 5 бит. Зная количество информации, которое несет один знак нашего алфавита, и количество знаков в сообщении, мы можем найти какое количество информации содержит наше сообщение.
Итак, наше сообщение содержит 30 бит.
4. Этап обобщения и закрепления нового материала.
1) Какое количество информации содержит слово «ИНФОРМАТИКА», если считать, что алфавит состоит из 32 букв? (55 битов)
2) Определить количество информации, содержащееся в слове из 10 символов, если известно, что мощность алфавита равна 32 символам. (50 бит)
3) Сколько бит информации содержится в сообщении, состоящем из 5 символов, при использовании алфавита, состоящего из 64 символов. (6 битов)
4) Определить информативность сообщения «А + В = С», если для описания математических формул необходимо воспользоваться 64-символьным алфавитом. (30 бит)
5) Для представления числовых данных используют 16-ричный алфавит, включающий знаки математических действий. Сколько битов информации содержит выражение «32 * 5 = 160»? (32 бита)
6) Практическая работа № 2. «Тренировка ввода текстовой и числовой информации с помощью клавиатурного тренажера»
5. Рефлексия.
Измерение информации. Алфавитный подход к измерению информации. Мощность алфавита. Информационный объем текста
Алфавитный подход к измерению информации Вам хорошо известно, что для измерения таких величин, как, например, расстояние, масса, время, существуют эталонные единицы. Для расстояния — это метр, для массы — килограмм, для времени — секунда. Измерение происходит путем сопоставления измеряемой величины с эталонной единицей. Сколько раз эталонная единица укладывается в измеряемой величине, таков и результат измерения. Следовательно, и для измерения информации должна быть введена своя эталонная единица. Алфавитный подход позволяет измерять информационный объем текста на некотором языке (естественном или формальном), не связанный с содержанием этого текста.
Алфавит. Мощность алфавита
Под алфавитом мы будем понимать набор букв, знаков препинания, цифр, скобок и др. символов, используемых в тексте. В алфавит также следует включить и пробел, т. е. пропуск между словами.
Полное число символов в алфавите принято называть мощностью алфавита. Будем обозначать эту величину буквой N. Например, мощность алфавита из русских букв и отмеченных дополнительных символов равна 54:33 буквы + 10 цифр + 11 знаков препинания, скобки, пробел.
Информационный вес символа
При алфавитном подходе считается, что каждый символ текста имеет определенный информационный вес. Информационный вес символа зависит от мощности алфавита. А каким может быть наименьшее число символов в алфавите? Оно равно двум! Скоро вы узнаете, что такой алфавит используется в компьютере. Он содержит всего 2 символа, которые обозначаются цифрами «0» и «1». Его называют двоичным алфавитом. Изучая устройство и работу компьютера, вы узнаете, как с помощью всего двух символов можно представить любую информацию.
Информационный вес символа двоичного алфавита принят за единицу информации и называется 1 бит.
Алфавитный подход к определению количества информации
Тип урока: Объяснение нового материала (01.10.08)
Формировать у учащихся понимание алфавитного подхода к измерению информации.
Развивать операциональное мышление и коммуникативную компетентность при обработке информации.
Воспитывать восприятие компьютера как инструмента информационной деятельности человека и бережного отношения к компьютеру.
I. Организационный момент.
II. Актуализация знаний.
III. Изложение нового материала.
V. Подведение итогов урока.
VI. Домашнее задание.
Урок проводится в компьютерном классе, доска, мел.
Основные понятия: алфавит, мощность алфавита, информационный вес символа в алфавите, производные единицы измерения информации.
I. Организационный момент
Учитель приветствует учащихся и отмечает отсутствующих.
II. Актуализация знаний
• Какое событие можно назвать информативным?
(событие информативно при условии:
1) произошло как минимум одно из двух возможных событий;
2) информация понятна, достоверна, объективна, полезна.)
• В чем заключается содержательный подход к измерению информации?
(в содержательном подходе рассматривается информативность равновероятностных событий.)
• Какую формулу используют для нахождения количества информации?
(Для нахождения количества информации используют формулу:
где N – количество всех возможных событий;
х – количество информации, содержащееся в данном сообщении.)•
Какую минимальную единицу используют для измерения количества информации?
(в качестве минимальной единицы информации используется 1 бит информации.)
Учитель предлагает детям ответить на следующие вопросы:
Сколько символов в компьютерном алфавите?
Как найти количество информации в тексте?
III. Изложение нового материала.
Вы научились определять количество информации, которое содержится в сообщениях, уменьшающих неопределенность наших, т.е. мы рассматривали информацию со своей точки зрения – с позиции человека. Для нас количество информации зависит от ее содержания, понятности и новизны. Однако любое техническое устройство не воспринимает содержание информации. Здесь не работают «неопределенность знаний» и «вероятность информации». Поэтому в вычислительной технике используется другой подход к измерению информации – алфавитный.
Алфавитный подход к измерению информации позволяет определить количество информации, заключенной тексте. Алфавитный подход является объективным, т.е. он не зависит от субъекта (человека), воспринимающего текст.
Множество символов, используемых при записи текста, называется алфавитом. Полное количество символов в алфавите называется мощностью (размером) алфавита. Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле:
Если весь текст состоит из К символов, то при алфавитном подходе размер содержащейся в нем информации равен:
где i — информационный вес одного символа в используемом алфавите,
К— количество символов в тексте,
I – количество информации, содержащейся в тексте (информационный объем текста).
Сравнивая объемы информации русского текста и английского, мы видим, что на английском языке информации меньше, чем на русском. Но ведь содержание не изменилось! Следовательно, при алфавитном подходе к измерению информации ее количество не зависит от содержания, а зависит от мощности алфавита и количества символов в тексте. С точки зрения алфавитного подхода, в толстой книге информации больше, чем в тонкой. При этом содержание книги не учитывается.
Правило для измерения информации с точки зрения алфавитного подхода:
1) Найти мощность алфавита – N
2) Найти информационный вес одного символа i из уравнения 
4) Найти количество информации – I (информационный объем всего сообщения)
Для измерения больших объемов информации используют следующие единицы:
Книга, набранная с помощью компьютера содержит 150 страниц; на каждой странице – 40 строк, в каждой строке – 60 символов. Каков объем информации в книге?
Значит, страница содержит 40*60=2400 байт информации.
Объем всей информации в книге (в разных единицах):
2 400*150=360 000 байт; 360 000/1024=351,5625Кб; 351,5625/1024=0,34332275Мб
Ответьте на вопросы, поставленные в начале урока.
1) Сколько символов в компьютерном алфавите?
(Алфавит из 256 символов используется для представления текстов в компьютере).
2) Как найти количество информации в тексте?
(Чтобы найти количество информации в тексте надо:
1. Найти мощность алфавита – N
2. Найти информационный вес одного символа i из уравнения
4. Найти количество информации – I (информационный объем всего сообщения)
Вычислите информационный объем сообщения: Наступили холода, при условии, что один символ кодируется 1 байтом.
(Решение: K = 16, i = 1 байт, следовательно I = 16 байт = 16*8 бит = 128 бит)
3Кб в байтах и битах (3*1024байт = 3072байт*8 = 24576 бит)
5920 бит в байтах и Кб (5920 бит/8 =740 байт/1024=0,72Кб)
1. Наиболее объективным методом измерения информации является алфавитный подход
2. Информативность сообщения зависит от мощности используемого алфавита
3. При измерении информации рассматриваются объекты окружающего мира, описанные языковыми средствами.
VI. Подведение итогов урока.
Учитель выставляет оценки учащимся, выполнявшим задания у доски, комментируя их.
VII. Домашнее задание.
И.Семакин «Информатика» Базовый курс Учебник 7-9 классы § 4. Вопросы и задания стр. 24-25.
По желанию, выполнить творческое задание:
Составить кроссворд по теме «Определение количества информации».
Место работы: школьный медиокласс по расписанию его работы.