в чем смысл бутылки клейна
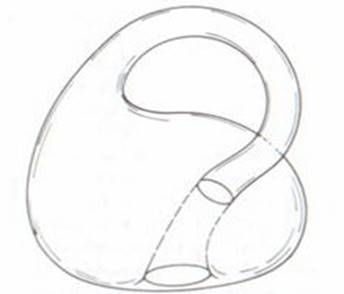
Бутылка Кляйна
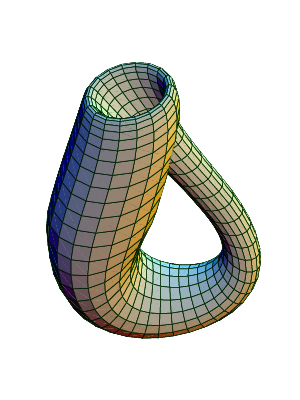
Кстати, бытует мнение, что бутылка — на самом деле не «бутылка» (нем. Flasche), а созвучное ей слово «поверхность» (Fläche).
В чем особенность бутылки Клейна и отличие ее от обычной бутылки? «Нормальная» бутылка имеет традиционное устройство: две поверхности (внутреннюю и наружную) и край (горлышко). Бутылка Клейна лишена и первого, и второго, и третьего: ее наружная поверхность «незаметно» (непрерывно) превращается во внутреннюю, подобно тому, как одна поверхность листа Мебиуса неожиданно для нас становится другой.
Несмотря на то, что трехмерное пространство не допускает существования бутылки Клейна (в этом случае непременно бутылка должна будет пересекаться с собой), всегда есть возможность получить ее в своем воображении. Для этого представим себе трубку, в одном конце которой предусмотрено отверстие. В него, предварительно слегка оттянув и загнув вверх, вставим противоположный край. После этого необходимо склеить концы и любоваться удивительным явлением — бутылкой Клейна, возможной без самопересечения только в четырехмерном пространстве.
Писатель-фантаст Стифен Барр, не смирившийся с невозможностью увидеть наяву настоящую бутылку Клейна, придумал «складывать» ее из обычного листа бумаги. Конечно, эта конструкция также не будет являться бутылкой Клейна в полном смысле слова (ну никуда нам не деться из трехмерного пространства!), однако, в отличие от попыток на стекле — некоторые высококлассные стеклодувы создают стеклянные псевдо-бутылки, делая дополнительное отверстие в стенке — бумага скроет обязательное отверстие — место самопересечения бутылки. Для того чтобы получить бумажную бутылку Клейна, сначала следует склеить края листа бумаги, предварительно перегнутого пополам, чтобы получилась трубка. Одну из половинок листа необходимо прорезать перпендикулярно склеенным сторонам таким образом, чтобы расстояние между прорезью и верхним краем трубки соответствовало приблизительно ¼ листа. Затем, согнув «конструкцию» пополам, нужно провести ее нижний край в прорезь, после чего склеить верхнее и нижнее основания.
Эксперименты с бутылкой Клейна
Дата публикации: 25.11.2014 2014-11-25
Статья просмотрена: 3648 раз
Библиографическое описание:
Первушкина, Е. А. Эксперименты с бутылкой Клейна / Е. А. Первушкина, Т. Д. Марушина. — Текст : непосредственный // Молодой ученый. — 2014. — № 21.1 (80.1). — С. 244-246. — URL: https://moluch.ru/archive/80/13829/ (дата обращения: 08.12.2021).
В данной статье представлены опыты с бутылкой Клейна. Поставлена проблема и решена экспериментально, прогнозирования экспериментов с разрезанием модели бутылки Клейна. Были выявлены ее свойства.
Ключевые слова: бутылка Клейна, лист Мебиуса, трехмерное пространство, топологическая поверхность.
Abstract. The article presents a series of experiments with the Klein bottle. Solves the problem of forecasting the result of the experiment with cutting the Klein bottle. We have also identified its properties.
Keywords: The Klein bottle, the Möbius strip, a three-dimensional space, topological surface.
Бутылка Клейна была описана немецким ученым Ф. Клейном в 1882 году.
С бутылкой Клейна знакомятся в высших учебных заведениях в курсе геометрии. Эта модель интересна тем, что ее свойства нельзя увидеть без проведения опытов, так как она не может существовать в нашем трехмерном пространстве. Модели, которые мы видим в магазинах, как сувенир имеют отдаленное представление о бутылки Клейна. Интересна возможность выявления свойств бутылки Клейна с помощью экспериментов.
Рис.1. Бутылка Клейна
Бутылка Клейна – это неориентируемая определённая поверхность [1, с. 352]. Она частично связана с лентой Мёбиуса (прямоугольная лента, полученная склеиванием противоположных сторон с поворотом на 180 градусов [3]) и проективной плоскостью.
Изготовление бутылки Клейна




 |  |
 |
Рис. 2. Изготовление бутылки Клейна
Сложите квадрат пополам и соедините его стороны, обозначенные пунктиром на рис.1 а). Сделайте прорезь на обращенной к вам половине квадрата, перпендикулярно склеенным сторонам рис.1 б). Между верхним краем и прорезью трубки должно быть расстояние равное четверти стороны квадрата. Перегнув модель пополам вдоль прямой А, протащите нижний край трубки сквозь прорезь, верхнее и нижнее основания трубки склейте друг с другом в соответствии со стрелками рис.1 в).
Видим, что склеить бутылку Клейна довольно сложно. Из прозрачного материала эта модель будет более наглядной. Далее проведем ряд экспериментов с бутылкой Клейна, описанных в таблице 1.
Вначале будут сделаны предположения, какой будет результат, затем проводится проверка высказанных нами предположений.
Разрезание бутылки Клейна


 |
Высказанное предположение подтвердилось.


 |
Высказанное предположение подтвердилось.

В результате мы получили два листа Мебиуса и цилиндр.
1. Склеили Бутылку Клейна и выполнили разрез посередине. Перед этим было высказано предположение, что результатом будет два листа Мебиуса. Данное высказывание подтвердилось.
2. Склеили бутылку Клейна, выполнили разрез по краю. Перед этим было высказано предположение, что получиться лист Мебиуса. Данное высказывание подтвердилось.
3. Склеили модель, выполнили два разреза по краям. Перед этим было высказано предположение, что результатом станет три листа Мебиуса. Высказанное предположение не подтвердилось. В результате были получены 2 листа Мебиуса и цилиндр.
Из проведенных нами опытов можно выделить следующие свойства бутылки Клейна:
2. Число Бетти – это число разрезов, которые можно провести так, чтобы поверхность не распалась на два отдельных куска [2, с. 507]. Так как бутылка Клейна не имеет краев (то есть поверхность замкнутая), то каждый разрез должен иметь форму какой-нибудь простой замкнутой кривой, поэтому число Бетти для нашей модели равно 2.
3. Хроматическое число (минимальное число цветов, в которые можно раскрасить модель так, чтобы концы любого ребра имели разные цвета) [5, с. 74]. Хроматическое число бутылки Клейна равно шести. Это означает, что на данной поверхности можно так расположить 6 областей разных цветов, чтобы 5 областей имели общие границы с шестой областью.
4. Бутылка Клейна является двумерным дифференцируемым неориентируемым многообразием [6, с. 208]. Она, в отличие от листа Мёбиуса, является замкнутым многообразием, то есть компактным многообразием без края.
5. Она не может быть вложена в трёхмерное евклидово пространство Е3 (только погружена), но вкладывается в Е4.
6. Бутылка Клейна может быть получена склеиванием по краю двух лент Мёбиуса. Но в обычном трехмерном евклидовом пространстве Е3 сделать это невозможно, не создав самопересечения.
Выполняя опыты, мы наблюдали затем, что происходит с бутылкой Клейна и делали правильные предположения. В то время как изначально наши предположения могли быть неверными. Значит, именно проведенные нами опыты делают свойства построенной поверхности более доступными для понимания.
В результате проведенных опытов, мы убедились, что действительно бутылка Клейна не может существовать в трехмерном пространстве, а лишь в четырехмерном. В наше время её можно встретить в магазинах, в рекламе, а также в шоу фокусников (иллюзионист, забравшись в бутылку, остается на половину погруженным в нее) [4, с. 28]. Изготовить бутылку Клейна из стекла достаточно сложно, поэтому она имеет высокую стоимость и применяется крайне редко.
1. Атанасян Л.С., Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. инс-ов. Ч-2. – М.: Просвещение, 1987. – 352 с.
2. Гарднер М. Математические головоломки и развлечения. – М.: Мир, 1971. – 507 с.
3. Марушина Т.Д. Разрезание лент // Исследования в области естественных наук. 2014. № 7 [Электронный ресурс]. URL: http://science.snauka.ru/2014/07/7567 (дата обращения: 09.08.2014).
4. Пономарева Е.И., Первушкина Е.А. Развитие креативности школьников при обучение математике в 5-6 классах с использованием интерактивных геометрических средств // Перспективы науки. – 2011. – № 16. – С. 27-34.
6. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. – М.: МИРОС.КПЦ «Марта», 1992. – 208 с.
Чем необычна бутылка Клейна? и зачем её сделали
Впервые упоминание о нем появилось в 1882 году, а автором был немецкий математик Феликс Клейн, создатель нового направления в геометрии.
А с точки зрения физики?
Как представить себе, на что похожа поразительная «бутылка» в реальности?
Оказывается, невозможно построить абсолютно правильную модель этого объекта в нашем трехмерном мире: здесь будет наблюдаться пересечение поверхности, что напрочь отсутствует в четырехмерном измерении.
Вывод: истинная «бутылка Клейна» может существовать только в четырехмерном измерении!
http://www.liveinternet.ru/users/s200170/post168142680
Тебе Википедию забанили?
Бутылка Клейна — неориентируемая (односторонняя) поверхность, впервые описанная в 1882 году немецким математиком Ф. Клейном. Она тесно связана с лентой Мёбиуса и проективной плоскостью. Название, по-видимому, происходит от неправильного перевода немецкого слова Fläche (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка); затем это название вернулось в таком виде в немецкий.
Чтобы построить модель бутылки Клейна, понадобится бутылка с двумя дополнительными отверстиями: в донышке и в стенке. Горлышко бутылки нужно вытянуть, изогнуть вниз и, продев его через отверстие в стенке, присоединить к отверстию на дне бутылки. Для настоящей бутылки Клейна в четырёхмерном пространстве отверстие в стенке не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве.
В отличие от обыкновенного стакана, у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара, можно пройти путь изнутри наружу, не пересекая поверхность (то есть на самом деле у этого объекта нет «внутри» и нет «снаружи»).
Кстати, воду в бутылку Клейна налить все-таки можно.
Бутылка Клейна не имеет края и к ней неприменимы понятия «внутри» и «снаружи» и может существовать только в четырехмерном измерении!
Методическая публикация «Ф. Клейн и его бутылка»
Муниципальное бюджетное учреждение дополнительного образования Собинского района
Детский (подростковый) центр г. Лакинска
Удивительная Бутылка Клейна
педагог дополнительного образования
Мартынова Елена Викторовна
Феликс Христиан Клейн (1849-1925)
Научная карьера Феликса Клейна развивалась так стремительно, как ни одна другая в немецкой истории.
Он стал ординарным профессором, достиг вершины научной иерархии, когда ему исполнилось всего двадцать три года.
Клейн напечатал ряд работ о решении уравнений 5-й, 6-й и 7-й степеней, об интегрировании дифференциальных уравнений, об абелевых функциях, о неевклидовой геометрии, исследовал теорию волчка.
Знаменитый математик был избран иностранным членом Петербургской академии наук, член-корр. Берлинской академии наук, тайным советником и представителем Университета в верхней палате Парламента Пруссии.
В 1872 году Клейн становится профессором Эрлангенского университета. Здесь он опубликовал свою знаменитую » Эрлангенского программу» («Сравнительное рассмотрение новых геометрических исследований»). Программа привлекла внимание математиков всей Европы. Клейн доказал непротиворечивость геометрии Лобачевского.
Влияние «Эрлангенской программы» на дальнейшее развитие геометрии было исключительно велико.
После «Эрлангенской программы» Клейн обращается к теории алгебраических функций.
Он опубликовал более 20 работ по неевклидовой геометрии, теории групп Ли, теории многогранников и эллиптическим функциям.
Он построил пример односторонней поверхности – «бутылку Клейна», начал издавать « Энциклопедию математических наук ».
В Мюнхенском университете ему удалось организовать комплексное обучение инженеров, кроме технических знаний они получали сведения из точных и естественнонаучных дисциплин.
Клейн организовал в Мюнхене « Математический кружок », где встречались математики и представители крупной промышленности и бизнеса.
Феликс Клейн работал в университетах Гёттингена, Берлина, Эрлангена, Мюнхена, Лейпцига. В 1888 году он вновь вернулся в Гёттинген, где работал до конца своей жизни.
Ф.Клейн вел факультативные курсы по разным предметам, от теории чисел до технической механики. Лекции Клейна пользовались исключительным успехом, он увлекал слушателей научными перспективами и показывал романтику и интригу математических исследований.
В начале XX века Клейн принял активное участие в реформе школьного образования в ряде стран.
И в книгах, и на лекциях Клейн неустанно подчеркивал, что математика должна заниматься не только задачами, которые рождаются внутри нее самой, но распространяться на все области знания, принося туда идеи порядка и оформляя закономерности реальной жизни на своем универсальном языке.
В 1915 году Феликса Клейна увлекли новые физические идеи А.Эйнштейна. Он начал читать курс лекций по теории инвариантов и их приложениям в классической и специальной теории относительности. Результатом его изысканий стала серия статей.
Всю свою жизнь Клейн старался раскрыть внутренние связи между отдельными ветвями математики, между математикой, физикой и техникой.
Многогранна организационная и общественная деятельность Клейна. 50 лет руководил он изданием одного из основных математических журналов «Mathematische Annalen». Своеобразной лебединой песней Клейна стали его «Лекции о развитии математики в XIX столетии».
Значительную часть времени и сил тратил Клейн на разработку проблем школьного преподавания математики и подготовку учителей, чем до него не занимался ни один математик такого масштаба.
Ещё при жизни Клейна вышел трёхтомник его сочинений.
Именем Феликса Клейна названы:
Математический центр в Германии;
Кратер на обратной стороне Луны;
Приз Европейского математического общества;
Медаль Международной комиссии по математическому образованию.
Имя Клейна носят математические объекты:
модель (интерпретация) Клейна;
бутылка (поверхность) Клейна.
Медаль имени Ф.Клейна
Невероятная Бутылка Клейна
Топологический объект «Бутылка Клейна» поражает своей необычностью, названа в честь автора – немецкого математика Феликса Клейна.
Бутылка Клейна и лист Мёбиуса. Сходство и различия
Свойства бутылки Клейна
Свойства листа Мёбиуса
1. Односторонняя поверхность
2. Непрерывная поверхность.
Любую точку поверхности можно соединить с другой, не отрываясь от поверхности
2. Непрерывная поверхность
3. Хроматический равен 6. Хроматический номер показывает, какое максимальное число областей на поверхности можно создать, чтобы у любой из них была общая граница со всеми другими.
3. Хроматический номер равен 6
Характеризуется числом Бетти
Число Бетти равно 2
Связность, или двухмерность, заключается в том, что при разрезании поверхность остается цельной.
Число Бетти равно 2
5. Поверхность не ориентируема
5. Поверхность не ориентируема
6. Является замкнутым двумерным многообразием без края.
7. Не может быть вложена в трёхмерное пространство (только погружена), но вкладывается в четырёхмерное пространство.
7. Вложен в трёхмерное пространство, а в двухмерное – погружен.
8. Может быть получена склеиванием по краю двух лент Мёбиуса.
8. Может быть получен разрезанием бутылки Клейна вдоль
9.Замкнутость и отсутствие края не связаны с понятием «расстояние»
9. Замкнутость и отсутствие края не связаны с понятием «расстояние»
10 . Ограничивает собой нулевой объём
Авторские модели Бутылки Клейна
1. Бутылка Клейна из пряжи . Для изготовления бутылки этим способом мы связали полотно, расширяющееся снизу и сверху с зауженной средней частью. Сшили его вдоль, оставив в шве отверстие для протягивания верхней части и загиба средней узкой части полотна – горлышка. Верхний и нижний края оставили круговыми отверстиями. Вывернули сшитое полотно, протянули верхнюю часть через отверстие, расправили и соединили открытое дно и верхнюю часть сшитого полотна. Бутылка Клейна готова!
ММы увлекли своим проектом ребят из объединений нашего центра. Вот такую бутылку Клейна из цветного пластилина сделали обучающиеся объединения «Умелые ручки» вместе с участниками проекта.
Ребята из объединения «Керамика» со своим педагогом Страздинь А.Е. помогли нам сделать бутылку Клейна из глины
А ещё мы сделали бутылку Клейна из двух пластиковых бутылок и гибкого шланга.
Где можно увидеть бутылку Клейна
Очень трудно предположить, какое применение может быть у бутылки Клейна. Но…
Аналог бутылки Клейна для трехмерного измерения можно изготовить в реальности. На прилавках сувенирных магазинов встречаются, например, стеклянные бутылки Клейна разных размеров, изготовленные умельцами-стеклодувами.
Это здание , похожее на бутылку Клейна, построено в городе Франкфурт-на-Майне.
Некоторые рукодельницы наловчились вязать шапочки в виде бутылки Клейна . Обычно они идут в комплекте с шарфиками, скрепленными в ленту Мебиуса.
Презентация по математике на тему «Эта загадочная Бутылка Клейна»
Описание презентации по отдельным слайдам:
Окружная научная конференция школьников Эта загадочная Бутылка Клейна Автор работы: Макарова Анастасия Константиновна Студентка 1 курса ГБПОУ СО СГТ Научный руководитель : Макаричева Наталья Вячеславовна преподаватель ГБПОУ СО СГТ
Цель Сконструировать модель бутылки Клейна, определить и проверить удивительные свойства бутылки Клейна Задачи: 1. Изучить литературу 2. Изучить историю изобретения бутылки Клейна 3. Описать бутылку Клейна и процессы её изготовления 4. Показать использование бутылки Клейна на практике 5. Сравнить бутылку Клейна с листом Мёбиуса
Объект исследования Бутылка Клейна как модель односторонней поверхности Предмет исследования Свойства односторонней поверхности на примере бутылки Клейна
Что такое бутылка Клейна Бутылка Клейна — определенная неориентируемая поверхность первого рода, т.е. поверхность, у которой нет различия между внутренней и внешней сторонами, и которая, таким образом, в пространстве ограничивает собой нулевой объем
История изобретения бутылки Клейна Феликс Христиан Клейн – немецкий математик
Сравнительная характеристика бутылки Клейна и листа Мёбиуса Бутылка Клейна Лист Мёбиуса 1. Хроматический номер 2. Непрерывность 3. Ориентированность 4. Односторонность
Лента Мебиуса Лист Мёбиуса, петля Мёбиуса —топологический объект, простейшая неориентируемая поверхность с краем, односторонняя при вложении в обычное трёхмерное Евклидово пространство R3
Топологические свойства бутылки Клейна 1.Хроматический номер 2. Непрерывность 3. Ориентированность
Конструирование бутылки Клейна Способ № 1. Получение бутылки Клейна из бумаги Способ № 2. Получение бутылки Клейна из стандартной пластмассовой бутылки Способ № 3. Получение бутылки Клейна из одного цилиндра
Конструирование бутылки Клейна Способ № 4. Получение бутылки Клейна из ткани Способ № 5. Получение бутылки Клейна склеиванием двух листов Мёбиуса Способ № 6. Получение бутылки Клейна из пластилина
Применение бутылки Клейна В качестве сувениров Соревнования по изготовлению бутылок
Эта загадочная Бутылка Клейна Автор работы: Макарова Анастасия Константиновна Студентка 1 курса ГБПОУ СО СГТ Научный руководитель : Макаричева Наталья Вячеславовна преподаватель ГБПОУ СО СГТ
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1374149
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
В России предложили учредить День семейного волонтерства
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
В России планируют создавать пространства для подростков
Время чтения: 2 минуты
В Москве новогодние утренники в школах и детсадах пройдут без родителей
Время чтения: 1 минута
Утверждено стратегическое направление цифровой трансформации образования
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.