в чем разница у гармонических и затухающих колебаний

Механические колебания: гармонические, затухающие и вынужденные колебания

Механические колебания

Содержание

1. Механические колебания

1.1 Механические колебания: гармонические, затухающие и вынужденные колебания

1.3 Разложение колебаний в гармонический спектр. Применение гармонического анализа для обработки диагностических данных

1.4 Механические волны, их виды и скорость распространения

1.5 Энергетические характеристики волны

Список использованных источников

Механические колебания

Механические колебания: гармонические, затухающие и вынужденные колебания

Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости (качание маятника часов, колебания струны или ножек камертона, напряжение между обкладками конденсатора в контуре радиоприемника, работа сердца).

В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т.д. Мы будем рассматривать механические колебания. Колебания, происходящие при отсутствии трения и внешних сил, называются собственными; их частота зависит только от свойств системы.

Простейшими являются гармонические колебания, т.е. такие колебания, при которых колеблющаяся величина (например, отклонение маятника) изменяется со временем по закону синуса или косинуса.

Дифференциальное уравнение гармонического колебания

Рассмотрим простейшую колебательную систему: шарик массой m подвешен на пружине.

В этом случае упругая сила F1 уравновешивает силу тяжести mg. Если сместить шарик на расстояние х, то на него будет действовать большая упругая сила (F1 +F). Изменение упругой силы по закону Гука пропорционально изменению длины пружины или смещению шарика х:

где k — жесткость пружины. Знак «-» отражает то обстоятельство, что смещение и сила имеют противоположные направления.

Сила F обладает следующими свойствами: 1) она пропорциональна смещению шарика из положения равновесия; 2) она всегда направлена к положению равновесия.

Уравнение второго закона Ньютона для шарика имеет вид:

, или .

Так как k и m — обе величины положительные, то их отношение можно приравнять квадрату некоторой величины w0, т.е. мы можем ввести обозначение . Тогда получим

Таким образом, движение шарика под действием силы вида (1) описывается линейным однородным дифференциальным уравнением второго порядка.

Легко убедиться подстановкой, что решение уравнения имеет вид:

где (w₀ t + a₀) = a — фаза колебаний; a₀ — начальная фаза при t = 0; w₀ — круговая частота колебаний; A — их амплитуда.

Итак, смещение x изменяется со временем по закону косинуса.

График гармонического колебания показан на рисунке. Период этих колебаний находится из формулы:

.

Для пружинного маятника получаем:

.

Круговая частота связана с обычной n соотношением: .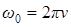

Энергия при гармоническом колебании

Выясним, как изменяется со временем кинетическая Еk и потенциальная Еп энергия гармонического колебания. Кинетическая энергия равна:

, (4)

Потенциальную энергию находим из формулы потенциальной энергии для упругой деформации и используя (3):

E_П. (5)

Складывая (4) и (5), с учетом соотношения , получим:

E = E_K + E_П = . (6)

Таким образом, полная энергия гармонического колебания остается постоянной в отсутствие сил трения, во время колебательного процесса кинетическая энергия переходит в потенциальную и наоборот.

Колебания, происходящие в системе при отсутствии внешних сил (но при наличии потерь на трение или излучение), называются свободными. Частота свободных колебаний зависит от свойств системы и интенсивности потерь.

Наличие трения приводит к затухающим колебаниям. Колебания с убывающей амплитудой называются затухающими.

Допустим, что на систему, кроме квазиупругой силы, действуют силы сопротивления среды (трения), тогда второй закон Ньютона имеет вид:

. (7)

Ограничимся рассмотрением малых колебаний, тогда и скорость системы будет малой, а при небольших скоростях сила сопротивления пропорциональна величине скорости:

, (8)

Подставим (8) в (7). Тогда

или

,

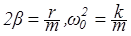
где b — коэффициент затухания, w₀ — круговая частота собственных колебаний. Тогда

График этой функции дан на рисунке.

Рис. 2. Затухающие колебания.

Период затухающих колебаний зависит от коэффициента трения и равен:

(11)

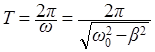
Вынужденные колебания. Резонанс

При составлении уравнения движения нужно учесть, кроме вынуждающей силы, также те силы, которые действуют в системе при свободных колебаниях, то есть квазиупругую силу и силу сопротивления среды. Тогда уравнение движения (второй закон Ньютона) запишется следующим образом:

.

Разделив это уравнение на m и перенеся члены с dx и d 2 x в левую часть получим неоднородное линейное дифференциальное уравнение второго порядка:

где — коэффициент затухания, — собственная частота колебаний системы. Решением этого уравнения будет:

Расчет дает значение резонансной частоты:

w_рез =

А_рез = . (14)

Чтобы определить резонансную частоту w_рез, нужно найти максимум функции (2.13) или, что то же самое, минимум выражения, стоящего под корнем в знаменателе. Продифференцировав это выражение по W и приравняв нулю, мы получим условие, определяющее w_рез:

Это уравнение имеет три решения: W = 0 и .

Решение, равное нулю, соответствует максимуму знаменателя. Из остальных двух решений отрицательное должно быть отброшено, как не имеющее физического смысла (частота не может быть отрицательной). Таким образом, для резонансной частоты получается одно значение: w_рез = . Подставив это значение частоты в (13), получим выражение для амплитуды при резонансе:

А_рез =

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы (частоты колебаний) показана графически на рисунке: b₁

Автоколебания

Источник