в чем разница между log и lg

03.01.202408.04.2022 admin 0 Comments

lg log в чем разница

Ответ

Проверено экспертом

Log — это обозначение любого логарифма
так

логарифм числа 5 по основанию6

а есть два уникальных особенных
— натуральный логарифм по основанию числа е
и десятичный

т.е. lg — это десятичный логарифм, один особенный случай логарифма log

Определение. Десятичный логарифм — логарифм по основанию 10.

Калькулятор десятичных логарифмов

Свойства десятичного логарифмов

lg x = log₁₀ x — так как основание десятичного логарифма равно 10.

lg( x · y ) = lg x + lg y

lg x y = lg x — lg y

lg 100 = lg 10 2 = 2

lg 1000 = lg 10 3 = 3

Запишем очевидное равенство:

lg b · lg a = lg a · lg ab

Возведем 10 в соответствующие степени

10 lg b · lg a = 10 lg a · lg b

(10 lg b ) lg a = (10 lg a ) lg b

Используем формулы логарифма произведения и степени получим:

lg 6 = lg (2·3)= lg 2 + lg 3 = a + b ;

lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c ;

Вычислить log₉ 5 · log₂₅ 27.

Перейдем к основе 10:

log₉ 5 · log₂₅ 27 = lg 5 lg 9 · lg 27 lg 25

Используем свойство логарифма степени lg x n = n lg x :

lg 5 lg 9 · lg 27 lg 25 = lg 5 lg 3 2 · lg 3 3 lg 5 2 = lg 5 2 lg 3 · 3 lg 3 2 lg 5 = 3 4

Перейдем к основе 10:

log ₃₀ 8 = lg 8 lg 30 = lg 2 3 lg (3 · 10) =

Используем свойство логарифма степени, произведения, частного и то что 2= 10 5 :

= 3 lg 2 lg 3 + lg 10 = 3 lg 2 lg 3 + 1 = 3 lg 10 5 lg 3 + 1 = 3(lg 10 — lg 5) lg 3 + 1 = 3(1 — lg 5) lg 3 + 1 =

log₃₀ 8 = 3(1 — a ) b + 1

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Если b = a c c = log_ab, a,b,c принадлежат к действительным числам, b > 0, a > 0, a ≠ 1
a основа логарифма
Например: 2 3 = 8 => log₂8 = 3

Свойства логарифма

$log_a(b cdot c) = log_ab + log_ac$ показать пример

$log_afrac = log_ab — log_ac$ показать пример

$log_ab^n = n cdot log_ab$ показать пример

log_a(b ± c) — формула не существует

Антилогаритмуване

log_ab = log_ac ⇔ b = c
log_ab = c ⇔ a c = b, который b > 0, a > 0 и a ≠ 1

log_ab > log_ac ⇔ если a > 1, то b > c,
если 0 2 =

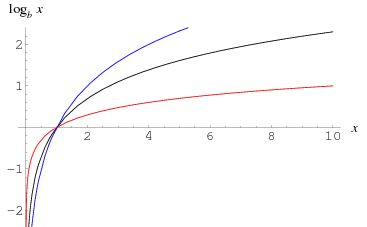
График логарифма

Источник

Десятичные и натуральные логарифмы

п.1. Десятичный логарифм и его свойства

Основание десятичных логарифмов $10\gt 1$, поэтому они обладают всеми свойствами логарифмов с основанием больше единицы (см. §30 данного справочника).

Но у десятичных логарифмов есть также целых ряд дополнительных свойств, благодаря которым в докомпьютерную эпоху они широко использовались для трудоемких вычислений. Роль калькулятора тогда выполняли логарифмическая таблица и логарифмическая линейка.

Число b	Стандартный вид	Характеристика	Мантисса b	Унифицированная запись	Логарифм числа $\lg b$
420	4,2·10 2	2	0,623	2,623	2,623
42	4,2·10 1	1	0,623	1,623	1,623
4,2	4,2	2	0	0,623	0,623
0,42	4,2·10 –1	–1	0,623	$\overline<1>,623$	–0,377
0,042	4,2·10 –2	–2	0,623	$\overline<2>,623$	–1,377

Если использовать унифицированную запись, как в представленной таблице, то мантисса всегда лежит в промежутке $0\lt \lg a\lt 1$. У чисел, отличающихся только порядком, мантисса одинакова. Можно составить таблицы мантисс и пользоваться ими для умножения и деления, «разбавляя» их несложным сложением и вычитанием целых характеристик по необходимости.

Первые таблицы логарифмов были изданы в 1617 году оксфордским математиком Бригсом. Таблицы пересчитывались, дополнялись и переиздавались вплоть до 70-х гг. ХХ века, когда на столах стали появляться калькуляторы.
Таблицы Брадиса, которыми по традиции пользуются наши школьники с 1921 года, издаются до сих пор и постепенно перекочевывают в Интернет.

Непосредственная связь десятичных логарифмов с десятичной системой исчисления делает их удобным инструментом для оценки порядка числа и сравнения чисел.

В практике приближенных вычислений используется следующая оценочная таблица:

Относительная погрешность этих приближений (кроме $\lg 3)$ $\delta\sim 0,5\text<%>$

Например:
Сравним $\log_23$ и $log_5⁡8$
Сравнивая с помощью оценки, получаем: \begin \log_23=\frac<\lg 3><\lg 2>\approx\frac<0,5><0,3>=\frac53,\ \ \log_58=\frac<\lg 8><\lg 5>\approx\frac<0,9><0,7>=\frac97\\ \frac<35><21>\gt \frac<27><21>\Rightarrow \frac53\gt \frac97\Rightarrow\log_23\gt\log_58 \end

п.2. Натуральный логарифм и его свойства

Основание натуральных логарифмов e>1, поэтому они обладают всеми свойствами логарифмов с основанием больше единицы (см. §30 данного справочника).

Для приближенного вычисления значения натурального логарифма используется «ряд Меркатора»:

Например:
С точностью до первого слагаемого: $\ln 1,3=\ln(1+0,3)\approx 0,3$
До второго слагаемого: $\ln 0,3\approx 0,3-\frac<0,3^2><2>=0,255$
До третьего слагаемого: $\ln 0,3\approx 0,3-\frac<0,3^2><2>+\frac<0,3^3><3>=0,264$ и т.д.

Натуральные логарифмы настолько распространены в различных областях научных исследований, что когда вообще речь заходит «логарифмах», по умолчанию подразумевают именно их. Если же у вас в работе какие-то другие «логарифмы» (по основанию 2 или 10, например), это нужно уточнять.

п.3. Примеры

Пример 1. Найдите $x$:
a) $ \lg x=2\lg a+\lg 7 $
$\lg x=\lg a^2+\lg 7=\lg(7a^2)$
$x=7a^2$

Пример 2. Прологарифмируйте по основанию 10:
a) $x=\frac<3a^2\sqrt[3]>$ \begin \lg x=\lg\frac<3a^2\sqrt[3]>=\lg 3+\lg a^2+\lg\sqrt[3]-\lg c^5-\lg(a-b)=\\ =\lg 3+2\lg a+\frac73\lg b-5\lg c-\lg(a-b) \end

Расчет относительной погрешности приближения на границах окрестностей $|x|\lt 0,1$ и $|x|\lt 0,2$ представлен в таблице:

Источник

Логарифмы и их свойства

Обычно определение логарифма дают очень сложно и запутанно. Мы постараемся сделать это очень просто и наглядно.

Для того, чтобы разобраться, что такое логарифм, давайте рассмотрим пример:

Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.

Теперь при помощи этой таблицы введем понятие логарифма.

Логарифм от числа 32 по основанию 2 ($log_<2>(32)$) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:

Аналогично, глядя в таблицу получим, что:

Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.

Теперь дадим определение логарифма в общем виде:

Логарифмом положительного числа $b$ по основанию положительно числа $a$ называется степень $c$, в которую нужно возвести число $a$, чтобы получить $b$

Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:

Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:

Или логарифм шести по основанию 4:

На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!

Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм $log_<4>(6)$. Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6ке:

Значит $log_<4>(6)$ принадлежите промежутку от 1 до 2:

Как посчитать логарифм

Почему так? Это следует из определения показательной функций. Показательная функция не может быть $0$. А основание не равно $1$, потому что тогда логарифм теряет смысл – ведь $1$ в любой степени это будет $1$.

При этих ограничениях логарифм существует.

В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.

Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.

Теперь давайте разберем общий алгоритм вычисления логарифмов:

Давайте разберем на примерах.

Пример 1. Посчитать логарифм $9$ по основанию $3$: $log_<3>(9)$

Пример 2. Вычислить логарифм $\frac<1><125>$ по основанию $5$: $log_<5>(\frac<1><125>)$

Пример 3. Вычислить логарифм $4$ по основанию $64$: $log_<64>(4)$

Пример 4. Вычислить логарифм $1$ по основанию $8$: $log_<8>(1)$

Пример 5. Вычислить логарифм $15$ по основанию $5$: $log_<5>(15)$

Как понять, что некоторое число $a$ не будет являться степенью другого числа $b$. Это довольно просто – нужно разложить $a$ на простые множители.

$16$ разложили, как произведение четырех двоек, значит $16$ будет степенью двойки.

Разложив $48$ на простые множители, видно, что у нас есть два множителя $2$ и $3$, значит $48$ не будет степенью.

Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.

Десятичный логарифм

Натуральный логарифм

Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.

У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.

Свойства логарифмов

Давайте разберем несколько примеров на свойства логарифмов.

Пример 8. Воспользоваться формулой $3$. Логарифм от произведения – это сумма логарифмов.

Пример 9. Воспользоваться формулой $4$. Логарифм от частного – это разность логарифмов.

Пример 10. Формула $5,6$. Свойства степени.

Логично, что будет выполняться и такое соотношение:

Пример 11. Формулы $7,8$. Переход к другому основанию.

Источник

lg log в чем разница

Ответ

Проверено экспертом

Log — это обозначение любого логарифма
так

логарифм числа 5 по основанию6

а есть два уникальных особенных
— натуральный логарифм по основанию числа е
и десятичный

т.е. lg — это десятичный логарифм, один особенный случай логарифма log

Определение. Десятичный логарифм — логарифм по основанию 10.

Калькулятор десятичных логарифмов

Свойства десятичного логарифмов

lg x = log₁₀ x — так как основание десятичного логарифма равно 10.

lg( x · y ) = lg x + lg y

lg x y = lg x — lg y

lg 100 = lg 10 2 = 2

lg 1000 = lg 10 3 = 3

Запишем очевидное равенство:

lg b · lg a = lg a · lg ab

Возведем 10 в соответствующие степени

10 lg b · lg a = 10 lg a · lg b

(10 lg b ) lg a = (10 lg a ) lg b

Используем формулы логарифма произведения и степени получим:

lg 6 = lg (2·3)= lg 2 + lg 3 = a + b ;

lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c ;

Вычислить log₉ 5 · log₂₅ 27.

Перейдем к основе 10:

log₉ 5 · log₂₅ 27 = lg 5 lg 9 · lg 27 lg 25

Используем свойство логарифма степени lg x n = n lg x :

lg 5 lg 9 · lg 27 lg 25 = lg 5 lg 3 2 · lg 3 3 lg 5 2 = lg 5 2 lg 3 · 3 lg 3 2 lg 5 = 3 4

Перейдем к основе 10:

log ₃₀ 8 = lg 8 lg 30 = lg 2 3 lg (3 · 10) =

Используем свойство логарифма степени, произведения, частного и то что 2= 10 5 :

= 3 lg 2 lg 3 + lg 10 = 3 lg 2 lg 3 + 1 = 3 lg 10 5 lg 3 + 1 = 3(lg 10 — lg 5) lg 3 + 1 = 3(1 — lg 5) lg 3 + 1 =

log₃₀ 8 = 3(1 — a ) b + 1

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Если b = a c c = log_ab, a,b,c принадлежат к действительным числам, b > 0, a > 0, a ≠ 1
a основа логарифма
Например: 2 3 = 8 => log₂8 = 3

Свойства логарифма

$log_a(b cdot c) = log_ab + log_ac$ показать пример

$log_afrac = log_ab — log_ac$ показать пример

$log_ab^n = n cdot log_ab$ показать пример

log_a(b ± c) — формула не существует

Антилогаритмуване

log_ab = log_ac ⇔ b = c
log_ab = c ⇔ a c = b, который b > 0, a > 0 и a ≠ 1

log_ab > log_ac ⇔ если a > 1, то b > c,
если 0 2 =

График логарифма

Источник

Логарифмы

Определение логарифма

Понятие логарифма и основного логарифмичесгого тождества

Понятие логарифма и основного логарифмическое тождества состоят в тесной зависимости, т.к. определение логарифма в математической записи и является основным логарифмическим тождеством.

Основное логарифмическое тождество вытекает из определения логарифма:

Логарифмом называют показатель степени n, при возведении в которую числа а получают число b.

Показательное уравнение a^n=b при a > 0, a ne 1 не имеет решений при неположительном b и имеет единственный корень при положительном b. Этот корень называется логарифмом числа b по основанию а и записывают:

Основное логарифмическое тождество

4 log₂ 7 =2 2 log₂ 7 = (2 log₂ 7 ) 2 = 7 2 = 49

2 1 + log₂ 7 = 2 · 2 log₂ 7 = 2 · 7 = 14

Что такое логарифм и как его посчитать

Логарифм имеет следующий вид:

где a – это основание логарифма,

b – это аргумент логарифма

Чтобы узнать значение логарифма приравняем его к X. и преобразовываем в и преобразовываем в Запомните, что именно основание (оно выделено красным) возводится в степень.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!

Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:

Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.

Два очевидных следствия определения логарифма

log a 1 = 0 ( a > 0, a ≠ 1 )

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень – единицу.

Логарифм. Свойства логарифма (корень логарифма, смена основания).

Корень логарифма из положительного числа равен логарифму подкоренного выражения, деленному на показатель корня/Логарифм. Свойства логарифма (корень логарифма, смена основания).
Использование свойств логарифмов при решении логарифмических уравнений и неравенств
Для того, чтобы не ошибаться при решении логарифмических уравнений и неравенств, свойства логарифмов, перечисленные в предыдущем разделе, следует применять внимательно и аккуратно.
Например, если при решении уравнения или неравенства требуется преобразовать выражение
следует применять формулу
поскольку в противном случае можно потерять корни.
По той же причине при преобразовании выражений
log_a ( f (x) g (x)) и
следует использовать формулы:
Степень можно выносить за знак логарифма
И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:
log a ( f ( x ) 2 = 2 log a f ( x )
Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть – только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Логарифмы со специальным обозначением
Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.
Виды логарифмов
log_a b – логарифм числа b по основанию a ( a > 0, a ≠ 1, b > 0)
lg b – десятичный логарифм (логарифм по основанию 10, a = 10).
Сумма логарифмов. Разница логарифмов
Логарифмы с одинаковыми основаниями можно складывать: Логарифмы с одинаковыми основаниями можно вычитать: Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!
Вынесение показателя степени из логарифма
Вынесение показателя степени из логарифма:

Переход к новому основанию
Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.
Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.
Разберем на примере.
Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:
Теперь применим переход к новому основанию для второго логарифма: Подставим полученные результаты в исходное выражение:
Десятичные и натуральные логарифмы
Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log₁₀x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например,
lg ( x y ) = lg x + lg y ( x > 0, y > 0 )
Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e – иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам:
log a b = lg b lg a = ln b ln a ( a > 0, a ≠ 1, b > 0 )
Вычисление логарифма равносильно решению показательного уравнения
при условии a > 0, a ≠ 1; b > 0, где
при условии a > 0, a ≠ 1; b > 0, где
Найти логарифм: log ₄ 8
Обозначим log₄ 8 через x :
Перейдем к показательному уравнению:
Сведем показательное уравнение к основе 2 и решим его:
Найти x если : log _x 125 = 3 2
За определением логарифма имеем:
x = (5 3 ) 2/3 = 5 3·2/3 = 5 2 = 25
Формулировки и доказательства свойств
Покажем примеры использования свойства логарифма произведения: log₅(2·3)=log₅2+log₅3 и .
Приведем пример использования этого свойства логарифма: .
Вот пример использования этого свойства: .
Покажем пару примеров применения этого свойства логарифмов: и .
Также часто используется формула , которая удобна при нахождении значений логарифмов. Для подтверждения своих слов покажем, как с ее помощью вычисляется значение логарифма вида . Имеем . Для доказательства формулы достаточно воспользоваться формулой перехода к новому основанию логарифма a : .
Осталось доказать свойства сравнения логарифмов.
Область допустимых значений (ОДЗ) логарифма
Теперь поговорим об ограничениях (ОДЗ – область допустимых значений переменных).
Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:
Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
– это явно неверно, так как основание не может быть отрицательным, то есть корень – «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
10 примеров логарифмов с решением
1. Найти значение выражения 2. Найти значение выражения 3. Найти значение выражения 3. Найти значение выражения 4. Найти значение выражения 5. Найти значение выражения 5. Найти значение выражения 6. Найти значение выражения Сначала найдем значение Сначала найдем значение Для этого приравняем его к Х:Тогда изначальное выражение принимает вид:
7. Найти значение выражения 7. Найти значение выражения Преобразуем наше выражение: Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выражения 8. Найти значение выражения Так как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов: 9. Найти значение выражения 9. Найти значение выражения Так как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:
10. Найти значение выражения Обращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄: Обращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄:
Надеюсь, теперь вы разобрались, что такое логарифм.
Источник