в чем разница между кучей и стеком
Основные принципы программирования: стек и куча
Авторизуйтесь
Основные принципы программирования: стек и куча
Мы используем всё более продвинутые языки программирования, которые позволяют нам писать меньше кода и получать отличные результаты. За это приходится платить. Поскольку мы всё реже занимаемся низкоуровневыми вещами, нормальным становится то, что многие из нас не вполне понимают, что такое стек и куча, как на самом деле происходит компиляция, в чём разница между статической и динамической типизацией, и т.д. Я не говорю, что все программисты не знают об этих понятиях — я лишь считаю, что порой стоит возвращаться к таким олдскульным вещам.
Сегодня мы поговорим лишь об одной теме: стек и куча. И стек, и куча относятся к различным местоположениям, где происходит управление памятью, но стратегия этого управления кардинально отличается.
Стек — это область оперативной памяти, которая создаётся для каждого потока. Он работает в порядке LIFO (Last In, First Out), то есть последний добавленный в стек кусок памяти будет первым в очереди на вывод из стека. Каждый раз, когда функция объявляет новую переменную, она добавляется в стек, а когда эта переменная пропадает из области видимости (например, когда функция заканчивается), она автоматически удаляется из стека. Когда стековая переменная освобождается, эта область памяти становится доступной для других стековых переменных.
Из-за такой природы стека управление памятью оказывается весьма логичным и простым для выполнения на ЦП; это приводит к высокой скорости, в особенности потому, что время цикла обновления байта стека очень мало, т.е. этот байт скорее всего привязан к кэшу процессора. Тем не менее, у такой строгой формы управления есть и недостатки. Размер стека — это фиксированная величина, и превышение лимита выделенной на стеке памяти приведёт к переполнению стека. Размер задаётся при создании потока, и у каждой переменной есть максимальный размер, зависящий от типа данных. Это позволяет ограничивать размер некоторых переменных (например, целочисленных), и вынуждает заранее объявлять размер более сложных типов данных (например, массивов), поскольку стек не позволит им изменить его. Кроме того, переменные, расположенные на стеке, всегда являются локальными.
В итоге стек позволяет управлять памятью наиболее эффективным образом — но если вам нужно использовать динамические структуры данных или глобальные переменные, то стоит обратить внимание на кучу.
Куча — это хранилище памяти, также расположенное в ОЗУ, которое допускает динамическое выделение памяти и не работает по принципу стека: это просто склад для ваших переменных. Когда вы выделяете в куче участок памяти для хранения переменной, к ней можно обратиться не только в потоке, но и во всем приложении. Именно так определяются глобальные переменные. По завершении приложения все выделенные участки памяти освобождаются. Размер кучи задаётся при запуске приложения, но, в отличие от стека, он ограничен лишь физически, и это позволяет создавать динамические переменные.
Вы взаимодействуете с кучей посредством ссылок, обычно называемых указателями — это переменные, чьи значения являются адресами других переменных. Создавая указатель, вы указываете на местоположение памяти в куче, что задаёт начальное значение переменной и говорит программе, где получить доступ к этому значению. Из-за динамической природы кучи ЦП не принимает участия в контроле над ней; в языках без сборщика мусора (C, C++) разработчику нужно вручную освобождать участки памяти, которые больше не нужны. Если этого не делать, могут возникнуть утечки и фрагментация памяти, что существенно замедлит работу кучи.
В сравнении со стеком, куча работает медленнее, поскольку переменные разбросаны по памяти, а не сидят на верхушке стека. Некорректное управление памятью в куче приводит к замедлению её работы; тем не менее, это не уменьшает её важности — если вам нужно работать с динамическими или глобальными переменными, пользуйтесь кучей.
Заключение
Вот вы и познакомились с понятиями стека и кучи. Вкратце, стек — это очень быстрое хранилище памяти, работающее по принципу LIFO и управляемое процессором. Но эти преимущества приводят к ограниченному размеру стека и специальному способу получения значений. Для того, чтобы избежать этих ограничений, можно пользоваться кучей — она позволяет создавать динамические и глобальные переменные — но управлять памятью должен либо сборщик мусора, либо сам программист, да и работает куча медленнее.
Структуры данных. Неформальный гайд
Конечно, можно быть успешным программистом и без сакрального знания структур данных, однако они совершенно незаменимы в некоторых приложениях. Например, когда нужно вычислить кратчайший путь между двумя точками на карте, или найти имя в телефонной книжке, содержащей, скажем, миллион записей. Не говоря уже о том, что структуры данных постоянно используются в спортивном программировании. Рассмотрим некоторые из них более подробно.
Очередь
Итак, поздоровайтесь с Лупи!
Лупи обожает играть в хоккей со своей семьей. И под “игрой”, я подразумеваю:
Когда черепашки залетают в ворота, их выбрасывает на верх стопки. Заметьте, первая черепашка, добавленная в стопку — первой ее покидает. Это называется Очередь. Так же, как и в тех очередях, что мы видим в повседневной жизни, первый добавленный в список элемент — первым его покидает. Еще эту структуру называют FIFO (First In First Out).
Как насчет операций вставки и удаления?
После такой веселой игры в хоккей, Лупи делает для всех блинчики. Она кладет их в одну стопку.
Когда все блинчики готовы, Лупи подает их всей семье, один за одним.
Заметьте, что первый сделанный ею блинчик — будет подан последним. Это называется Стек. Последний элемент, добавленный в список — покинет его первым. Также эту структуру данных называют LIFO (Last In First Out).
Добавление и удаление элементов?
Вы когда-нибудь видели башню плотности?
Все элементы сверху донизу расположились по своим местам, согласно их плотности. Что случится, если бросить внутрь новый объект?
Он займет место, в зависимости от своей плотности.
Примерно так работает Куча.
Куча — двоичное дерево. А это значит, что каждый родительский элемент имеет два дочерних. И хотя мы называем эту структуру данных кучей, но выражается она через обычный массив.
Также куча всегда имеет высоту logn, где n — количество элементов
На рисунке представлена куча типа max-heap, основанная на следующем правиле: дочерние элементы меньше родительского. Существуют также кучи min-heap, где дочерние элементы всегда больше родительского.
Несколько простых функций для работы с кучами:
Добавление элемента в существующую кучу
Для начала, мы добавляем элемент в самый низ кучи, т.е. в конец массива. Затем мы меняем его местами с родительским элементом до тех пор, пока он не встанет на свое место.
Максимальное количество проходов цикла while равно высоте дерева, или logn, следовательно, трудоемкость алгоритма — O(logn).
Извлечение максимального элемента кучи
Первый элемент в куче — всегда максимальный, так что мы просто удалим его (предварительно запомнив), и заменим самым нижним. Затем мы приведем кучу в правильный порядок, используя функцию:
И вновь максимальное количество вызовов функции maxHeapify равно высоте дерева, или logn, а значит трудоемкость алгоритма — O(logn).
Делаем кучу из любого рандомного массива
Окей, есть два пути сделать это. Первый — поочередно вставлять каждый элемент в кучу. Это просто, но совершенно неэффективно. Трудоемкость алгоритма в этом случае будет O(nlogn), т.к. функция O(logn) будет выполняться n раз.
Более эффективный способ — применить функцию maxHeapify для ‘под-кучи’, от (currSize/2) до первого элемента.
Сложность получится O(n), и доказательство этого утверждения, к сожалению, выходит за рамки данной статьи. Просто поймите, что элементы, находящиеся в части кучи от currSize/2 до currSize, не имеют потомков, и большинство образованных таким образом ‘под-куч’ будут высотой меньше, чем logn.
Действительно, зачем это все?
Кучи нужны для реализации особого типа сортировки, называемого, как ни странно, “сортировка кучей”. В отличие от менее эффективных “сортировки вставками” и “сортировки пузырьком”, с их ужасной сложностью в O(n 2 ), “сортировка кучей” имеет сложность O(nlogn).
Реализация до неприличия проста. Просто продолжайте последовательно извлекать из кучи максимальный (корневой) элемент, и записывайте его в массив, пока куча не опустеет.
Чтобы обобщить все вышесказанное, я написала несколько строчек кода, содержащего функции для работы с кучей, а для фанатов ООП оформила все в виде класса.
Легко, не правда ли? А вот и празднующая Лупи!
Лупи хочет научить своих детишек различать фигуры и цвета. Для этого она принесла домой огромное количество разноцветных фигур.
Через некоторое время черепашки окончательно запутались
Поэтому она достала еще одну игрушку, чтобы немного упростить процесс
Стало намного легче, ведь черепашки уже знали, что фигуры рассортированы по форме. А что, если мы пометим каждый столб?
Черепашкам теперь нужно проверить столб с определенным номером, и выбрать из гораздо меньшего количества фигурок нужную. А если еще и для каждой комбинации формы и цвета у нас отдельный столб?
Допустим, номер столба вычисляется следующим образом:
Фиолетовый треугольник
ф+и+о+т+р+е = 22+10+16+20+18+6 = Столб 92
Красный прямоугольник
к+р+а+п+р+я = 12+18+1+17+18+33 = Столб 99
Мы знаем, что 6*33 = 198 возможных комбинаций, значит нам нужно 198 столбов.
Назовем эту формулу для вычисления номера столба — Хеш-функцией.
(с кириллицей немного сложнее, но я оставил так для простоты. — прим.пер.)
Теперь, если нам нужно будет узнать, где хранится розовый квадрат, мы сможем вычислить:
Это пример хеш-таблицы, где местоположение элементов определяется хеш-функцией.
При таком подходе время, затраченное на поиск любого элемента, не зависит от количества элементов, т.е. O(1). Другими словами, время поиска в хеш-таблице — константная величина.
Ладно, но допустим мы ищем “карамельный прямоугольник” (если, конечно, цвет “карамельный” существует).
вернет нам 99, что совпадает с номером для красного прямоугольника. Это называется “Коллизия”. Для разрешения коллизии мы используем “Метод цепочек”, подразумевающий, что каждый столб хранит список, в котором мы ищем нужную нам запись.
Поэтому мы просто кладем карамельный прямоугольник на красный, и выбираем один из них, когда хеш-функция указывает на этот столб.
Ключ к хорошей хеш-таблице — выбрать подходящую хеш-функцию. Бесспорно, это самая важная вещь в создании хеш-таблицы, и люди тратят огромное количество времени на разработку качественных хеш-функций.
В хороших таблицах ни одна позиция не содержит более 2-3 элементов, в обратном случае, хеширование работает плохо, и нужно менять хеш-функцию.
Еще раз, поиск, не зависящий от количества элементов! Мы можем использовать хеш-таблицы для всего, что имеет гигантские размеры.
Хеш-таблицы также используются для поиска строк и подстрок в больших кусках текста, используя алгоритм Рабина-Карпа или алгоритм Кнута-Морриса-Пратта, что полезно, например, для определения плагиата в научных работах.
На этом, думаю, можно заканчивать. В будущем я планирую рассмотреть более сложные структуры данных, например Фибоначчиеву кучу и Дерево отрезков. Надеюсь, этот неформальный гайд получился интересным и полезным.
Переведено для Хабра запертым на чердаке программистом.
Русские Блоги
Разница между кучей и стеком
1. Куча и стек в разделе памяти программы
1.1 Введение
Стек автоматически выделяется и освобождается операционной системой, он используется для хранения значений параметров функции и локальных переменных, его действие аналогично стеку в структуре данных. Обратитесь к следующему коду:
Среди них локальные переменные, определенные в функции, помещаются в стек в определенном порядке, то есть между переменными соседних переменных не будет других переменных. Адрес стековой памяти растет в противоположном направлении от кучи, от верхнего к низу, поэтому адрес переменной, определенный позже, ниже первой определенной переменной.Например, адрес переменной s в приведенном выше коде меньше адреса переменной b, а адрес p2 меньше адреса s. Жизненный цикл данных, хранящихся в стеке, заканчивается выполнением функции.
1.2 Введение
Куча распределяется и освобождается программистом. Если программист не освобождает его, ОС перезапустит его в конце программы. Метод выделения аналогичен связанному списку. Обратитесь к следующему коду:
10-байтовое пространство памяти, на которое указывает p1, и 10-байтовое пространство памяти, на которое указывает p2, существуют в куче. Направление роста адресов памяти кучи противоположно направлению стека, от низкого к высокому, но следует отметить, что пространство памяти, примененное позже, не обязательно следует за пространством памяти, примененным для первого, то есть адрес, на который указывает p2, не обязательно больше, чем тот, на который указывает p1 Причина заключается в том, что, как только пространство памяти, к которому применяется, освобождается первым, пространство памяти, к которому применяется позднее, будет использовать ранее освобожденную память, в результате чего не будет никакой связи между выделенным пространством памяти по адресу. Если данные, хранящиеся в куче, не освобождаются, их жизненный цикл эквивалентен жизненному циклу программы.
2.3 Разница между кучей и стеком
Куча и стек фактически являются двумя способами для операционной системы управлять пространством памяти, занимаемым процессом.
(1) Методы управления разные. Стек автоматически выделяется и освобождается операционной системой без нашего ручного управления, применение и освобождение кучи контролируется программистом, который подвержен утечкам памяти;
(2) Размер пространства отличается. Размер стека, принадлежащего каждому процессу, намного меньше размера кучи. Теоретически, размер кучи, к которому может обратиться программист, равен размеру виртуальной памяти, размер стека процесса составляет 64 МБ, для Windows по умолчанию 1 МБ, и 64 бита для Linux по умолчанию 10 МБ;
(3) Направление роста другое. Направление роста кучи вверх, адрес памяти от низкого до высокого, направление роста стека вниз, а адрес памяти от высокого к низкому.
(4) Способ распределения другой. Куча выделяется динамически, статически не выделяется куча. У стека есть два метода размещения: статическое и динамическое. Статическое распределение выполняется операционной системой, например, распределение локальных переменных. Динамическое распределение выделяется функцией alloca, но динамическое выделение стека и кучи различаются. Его динамическое распределение освобождается операционной системой без нашей ручной реализации.
(6) Содержимое хранилища отличается. Содержимое хранится в стеке, адрес возврата функции, связанные параметры, локальные переменные и содержимое регистра. Когда основная функция вызывает другую функцию, чтобы сохранить текущую точку останова выполнения функции, вам необходимо использовать стек для ее достижения: адрес следующего оператора основной функции, то есть содержимого расширенного регистра указателя (EIP), а затем Нижний адрес текущего фрейма стека, то есть содержимое расширенного регистра базового указателя (EBP), затем фактические параметры вызываемой функции и т. Д. В общем случае он помещается в стек в порядке справа налево, а затем в локальную часть вызываемой функции. Переменные, обратите внимание, что статические переменные хранятся в сегменте данных или сегменте BSS и не помещаются в стек. Порядок выталкивания стека как раз противоположен.Наконец, вершина стека указывает на адрес следующего оператора основной функции, и основная программа начинает выполняться с этого адреса. Куча, как правило, верхняя часть кучи использует байтовое пространство для хранения размера кучи, а конкретное содержимое хранилища в куче заполняется программистом.
Как видно из вышесказанного, по сравнению с кучей и стеком, из-за использования большого количества malloc () / free () или new / delete, легко вызывать большую фрагментацию памяти и может вызывать переключение между пользовательским режимом и режимом ядра, а эффективность ниже. По сравнению с кучей, стек более широко используется в программе. Наиболее распространенным является то, что процесс вызова функции реализуется стеком. Адрес возврата функции, EBP, фактические параметры и локальные переменные хранятся в стеке. Хотя стек имеет много преимуществ, но поскольку он не такой гибкий по сравнению с кучей, иногда выделяется большой объем памяти, в основном с использованием кучи.
Будь то куча или стек, необходимо предотвратить незаконные выходы за пределы памяти при использовании памяти. Нелегальный доступ к памяти, вызванный выходом за пределы границ, может уничтожить данные программы в куче и стеке. Это может привести к тому, что программа будет работать в неопределенном состоянии, и ожидаемый результат не может быть получен. Причиной аварийного сбоя программы является то, на что мы должны обратить внимание при работе с памятью при программировании.
2. Куча и стек в структуре данных
В структуре данных куча и стек являются двумя общими структурами данных. Понимание определения, использования и различий между ними может использовать кучу и стек для решения многих практических задач.
2.1 Введение в стек
Существует два типа стеков: последовательный стек и цепной стек. Стек представляет собой линейную структуру, поэтому вы можете использовать массивы или связанные списки (односвязные списки, двусвязные списки или круговые связанные списки) в качестве базовой структуры данных. Стек, реализованный с использованием массива, называется последовательным стеком, а стек, реализованный с использованием связанного списка, называется цепочечным стеком.Различие между ними состоит в том, что адрес элементов в последовательном стеке является непрерывным, а адрес элементов в связном стеке не является непрерывным.
Структура стека показана ниже:
Основные операции стека включают в себя инициализацию, определение того, является ли стек пустым, проталкивание в и из стека и получение верхнего элемента стека. Далее в качестве примера используется последовательный стек, использующий язык C для простой реализации.
Запустите вышеуказанную программу и выведите результат:
2.2 Введение в кучу
2.2.1 Природа кучи
2.2.2 Основные операции кучи
(1) Учреждение
Если взять в качестве примера минимальную кучу, если для хранения элементов используется массив, массив имеет соответствующее представление дерева, но дерево не удовлетворяет условиям кучи, и элементы необходимо переставить. Дерево».
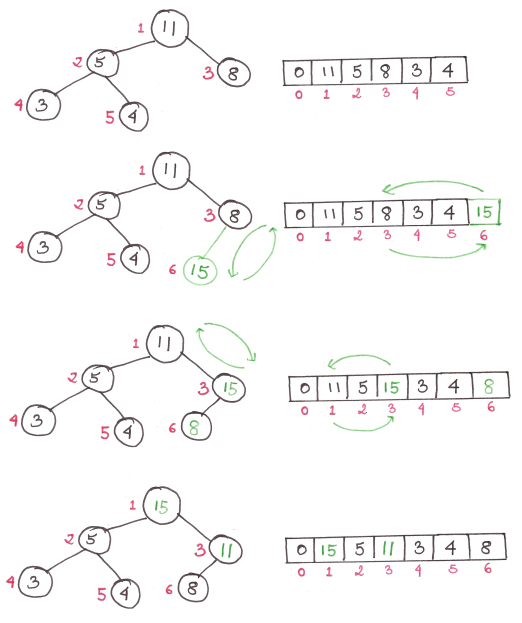
(2) Вставить
При вставке нового элемента в конец таблицы, то есть в конец массива, если вновь сформированное двоичное дерево не соответствует природе кучи, элементы необходимо переставить. На следующем рисунке показана вставка кучи на 15 Настройка.
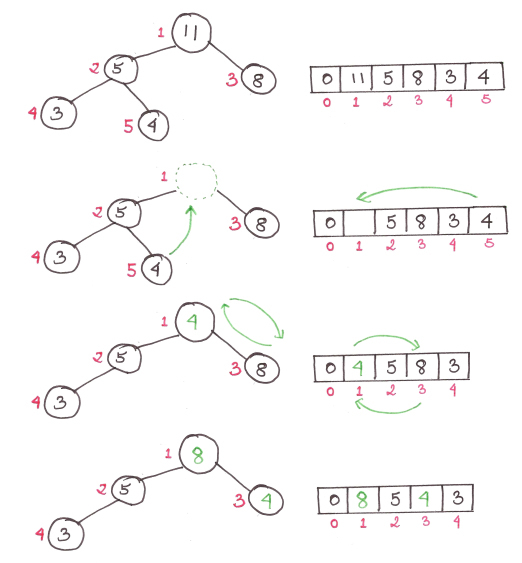
(3) Удалить.
При сортировке кучи удаление элемента всегда происходит в верхней части кучи, поскольку элемент в верхней части кучи является наименьшим (в маленькой верхней куче). Последний элемент в таблице используется для заполнения вакантной позиции, а дерево результатов обновляется в соответствии с условиями кучи.
2.2.3 Реализация операции кучи
(1) Введите код для достижения
Каждая вставка помещает новые данные в конец массива. Можно обнаружить, что родительский узел для корневого узла этих новых данных должен быть упорядоченной последовательностью. Теперь задача состоит в том, чтобы вставить эти новые данные в эти упорядоченные данные, что аналогично вставке данных в сортировку прямой вставкой. В упорядоченный интервал это «плавающая» настройка узла. Нетрудно написать код настройки кучи при вставке новых данных:
Поэтому при вставке данных в минимальную кучу:
(2) Удалить код для достижения
По определению, только 0-ые данные могут быть удалены из кучи каждый раз. Чтобы облегчить восстановление кучи, фактическая операция состоит в том, чтобы настроить последние данные массива и корневого узла, а затем выполнить корректировку от корневого узла сверху вниз.
При корректировке сначала найдите наименьший из левого и правого дочерних узлов. Если родительский узел не больше, чем наименьший дочерний узел, это означает, что корректировка не требуется. В противном случае измените наименьший дочерний узел на позицию родительского узла. В настоящее время родительский узел фактически не нужно менять на позицию наименьшего дочернего узла, поскольку это не конечная позиция родительского узла. Но логически, родительский узел заменяет наименьший дочерний узел, а затем учитывает влияние родительского узла на последующие узлы. Это эквивалентно процессу «утечки» данных из корневого узла. Код приведен ниже:
Согласно идее, могут быть разные версии кода. Выше приведена версия, обсуждаемая с одноклассником Сунь Рином. Спасибо за участие, читатель может дать его отдельно. Лично я предлагаю вам написать собственный код, основанный на вашем понимании процесса настройки кучи.Не смотрите на пример кода, чтобы понять алгоритм, но пишите код в соответствии с идеей алгоритма, иначе вы скоро забудете.
(3) укладка
После вставки и удаления кучи, подумайте, как накапливать данные. Вам нужно взять данные из массива один за другим, чтобы построить кучу, нет! Сначала посмотрите на массив, как показано ниже:
Напишите код для массива heaped:
2.2.4 Куча, специфичная для кучи приложений-сортировка
Поэтому операция вставки, описанная выше, не используется для завершения сортировки кучи, а только для операций построения кучи и корректировки узлов вниз. Операция сортировки кучи заключается в следующем:
(1) Стабильность. Сортировка кучи нестабильна.
(2) Анализ производительности сортировки кучи. Поскольку временная сложность восстановления кучи каждый раз составляет O (logN), всего N-1 операций регулировки кучи плюс N / 2 нисходящих корректировок, когда куча была установлена ранее, каждая сложность времени регулировки также равна O ( LogN). Добавление двух времен операции по-прежнему равно O (N * logN). Следовательно, временная сложность сортировки кучи составляет O (N * logN).
В худшем случае: если сортируемый массив упорядочен, операция сравнения со сложностью O (N * logN) все еще требуется, но отсутствует только операция перемещения;
Наилучший случай: если сортируемый массив расположен в обратном порядке, это касается не только операции сравнения сложности O (N * logN), но и операции обмена сложности O (N * logN). Общая сложность по времени все еще O (N * logN).
Следовательно, сортировка кучи и быстрая сортировка схожи по эффективности, но важный момент, который заключается в том, что сортировка кучи обычно лучше, чем быстрая сортировка, заключается в том, что первоначальное распределение данных не оказывает существенного влияния на эффективность сортировки кучи.