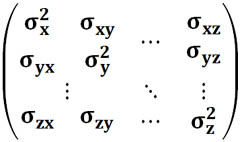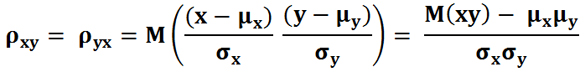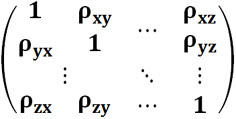в чем разница между корреляцией и ковариацией
Ковариация
которая может быть получена из первой формулы, используя свойства математического ожидания. Перечислим основные свойства ковариации.
1. Ковариация случайной величины с самой собой есть ее дисперсия.
2. Ковариация симметрична.
$$cov\left(X,\ Y\right)=cov\left(Y,\ X\right).$$
4. Постоянный множитель можно выносить за знак ковариации.
$$cov\left(cX,\ Y\right)=cov\left(X,\ cY\right)=c\cdot cov\left(X,\ Y\right).$$
5. Ковариация не изменится, если к одной из случайных величин (или двум сразу) прибавить постоянную величину:
$$cov\left(X+c,\ Y\right)=cov\left(X,\ Y+c\right)=cov\left(X+x,\ Y+c\right)=cov\left(X,\ Y\right).$$
9. Дисперсия суммы (разности) случайных величин равна сумме их дисперсий плюс (минус) удвоенная ковариация этих случайных величин:
$$D\left(X\pm Y\right)=D\left(X\right)+D\left(Y\right)\pm 2cov\left(X,\ Y\right).$$
$$M\left(X\right)=\sum^n_
$$M\left(Y\right)=\sum^n_
$$M\left(XY\right)=\sum_
Корреляция
Перечислим основные свойства коэффициента корреляции.
При копировании материала с сайта, обратная ссылка обязательна!
Повторение статистики для начала путешествия по науке о данных
Введение
Предположим, у нас есть диаграмма рассеяния, на которой каждая точка — это человек. На одной оси показан его профессиональный опыт в годах, на другой — доход.
В соответствии с диаграммой справа можно заключить, что между опытом и доходом нет никакой связи, то есть определенный опыт оплачивается по-разному.
Слева, наоборот, между признаками существует четкая линейная зависимость.
Ковариация и корреляция показывают, насколько тесно между собой связаны переменные набора данных.
N.B: в приведенном примере представлен двумерный вид данных (с двумя переменными). На практике статистики используют многомерные данные (со множеством переменных).
Ковариация
Ковариация — это мера зависимости между двумя или более случайных переменных.
С английского «covariance» = «co» (совместность/соединение) + «variance» (дисперсия). То есть ковариация похожа на дисперсию, но она применяется для сравнения двух переменных, где вместо суммы квадратов, мы получаем сумму векторного произведения.
Дисперсия показывает, насколько определенная переменная отличается от среднего значения, а ковариация — насколько две переменные отличаются друг от друга. Таким образом, можно утверждать следующее:
Ковариация измеряет дисперсию между двумя переменными.
Ковариация может быть отрицательной, положительной и нулевой: положительное значение показывает, что две переменные изменяются в одном направлении (если одна переменная увеличивается, то и вторая тоже увеличивается); отрицательное значение показывает, что две переменные изменяются в разных направлениях (одна увеличивается, вторая уменьшается); нулевая ковариация означает, что они изменяются независимо друг от друга.
Формула
Формулу сложно объяснить, но важно понять, что она означает:
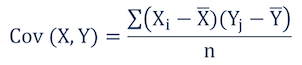
Предположим, что набор данных со случайными переменными представлен в виде вектора. Тогда в прошлом примере у нас есть два вектора для опыта и дохода. Ниже приведен порядок действий:
На втором этапе измеряется угол между двумя векторами. Если угол острый, то переменные тесно связаны между собой.
Ограниченность
Следует отметить, что несмотря на то, что ковариация измеряет зависимость между направлениями двух переменных, она не показывает тесноту этой зависимости.
На практике самая большая проблема с этой мерой заключается в том, что она зависит от используемой единицы измерения. Например, необходимо перевести годы опыта в месяцы. Тогда ковариация будет в 12 раз больше.
В этом случае на помощь приходит корреляция!
Корреляция
Корреляция — одна из наиболее распространенных мер в статистике, описывающая тесноту взаимосвязи между двумя случайными переменными. Она считается нормализованной версией ковариации. Давайте рассмотрим, почему…
Формула
Корреляция (обозначаемая греческой буквой «ро» — ρ) рассчитывается по следующей формуле:
Обратите внимание, что функциональная связь редко встречается на практике, так как две случайные переменные обычно не сопоставляются друг с другом на основе постоянного значения.
Корреляция, равная 0, означает, что между двумя переменными нет линейной зависимости. Тогда может быть отношение x = y².
Ключевые свойства
Корреляция — безразмерная величина, указывающая не только на направление взаимосвязи, но и на ее тесноту (в зависимости от того, насколько большим является абсолютное значение). Единицы измерения исключены из-за того, что ковариацию разделили на среднеквадратическое отклонение.
Напоследок необходимо запомнить, что корреляция не является причинно-следственной связью. Высокая корреляция между двумя случайными переменными просто означает, что они связаны друг с другом, но их взаимоотношение не обязательно должен иметь причинно-следственный характер. Доказать причинно-следственную связь можно только с помощью контролируемых экспериментов, при которых внешние переменные исключаются и эффекты двух данных переменных изолируются.
Русские Блоги
Популярное объяснение ковариации и коэффициента корреляции
Что такое ковариация (ковариация)?
Ковариация представляет собой общую ошибку двух переменных, которая отличается от дисперсии только одной переменной. Если тенденции изменения двух переменных одинаковы, то есть если одна из них больше, чем ее собственное ожидаемое значение, а другая также больше, чем ее собственное ожидаемое значение, то ковариация между двумя переменными положительна. Если тенденции изменения двух переменных противоположны, то есть одна из них больше, чем ее собственное ожидаемое значение, а другая меньше, чем ее собственное ожидаемое значение, то ковариация между двумя переменными отрицательна.
Это объяснение некой энциклопедии. и многое другое! Это еще более непонятно? Как для студентов нетехнических специальностей ясно и наглядно понять математические концепции ковариации и коэффициента корреляции? Это не имеет значения. Сегодня Red Stone использует яркие примеры, чтобы объяснить коэффициенты ковариации и корреляции простым для понимания образом.
1. Как возникает ковариация?
Проще говоря, ковариация отражает взаимосвязь между двумя переменными X и Y. Этот вид корреляции можно условно разделить на три типа: положительная корреляция, отрицательная корреляция и нерелевантность.
Что такое положительная корреляция? Например, чем больше площадь дома (X), тем выше общая цена дома (Y), а площадь дома положительно коррелирует с общей ценой дома;
Что такое отрицательная корреляция? Например, чем больше времени студент проводит за играми (X), тем хуже его успеваемость (Y), тогда игровое время и успеваемость имеют отрицательную корреляцию;
Что не имеет значения? Например, степень черного и белого цвета кожи человека (X) не имеет очевидной связи с его физическим здоровьем (Y), поэтому не имеет значения.
Давайте сначала рассмотрим первый случай, пусть переменная X и переменная Y будут соответственно:
X = [11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]
Y = [12 15 17 21 22 21 18 23 26 25 22 28 24 28 30 33 28 34 36 35]
Постройте совместное распределение X и Y по координатам:
Очевидно, что общий тренд Y увеличивается с увеличением X, то есть изменения Y и X происходят в одном направлении. В этом случае мы говорим, что X и Y положительно коррелированы.
Давайте снова рассмотрим второй случай, пусть переменная X и переменная Y будут соответственно:
X = [11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]
Y = [35 35 29 29 28 28 27 26 26 23 21 22 25 19 16 19 20 16 15 16]
Постройте совместное распределение X и Y по координатам:
Очевидно, что общая тенденция Y уменьшается с увеличением X, то есть изменения Y и X меняются местами. В этом случае мы говорим, что X и Y отрицательно коррелированы.
Давайте снова рассмотрим третий случай, пусть переменная X и переменная Y будут соответственно:
X = [11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]
Y = [16 16 28 17 20 26 20 17 21 15 12 29 24 25 16 15 21 13 17 25]
Постройте совместное распределение X и Y по координатам:
Очевидно, что нет никакой положительной или отрицательной корреляции между Y и X в общем тренде. В этом случае мы говорим, что X и Y не связаны.
На приведенном выше рисунке вся область разделена на четыре области I, II, III и IV посредством EX и EY, и большая часть X и Y распределена в областях I и III, и только небольшая часть распределена в областях II. и IV.
В области I, если выполняются X> EX и Y> EY, то (X-EX) (Y-EY)> 0;
В области II, если выполняется X EY, то (X-EX) (Y-EY) 0;
В области IV, если выполняются X> EX и Y 0; в областях II и IV (X-EX) (Y-EY) E ( X − E X ) ( Y − E Y ) > 0 E(X-EX)(Y-EY)>0 E ( X − E X ) ( Y − E Y ) > 0
Приведенная выше формула означает, что ожидание (X-EX) (Y-EY) больше нуля, то есть среднее значение (X-EX) (Y-EY) больше нуля.
Затем давайте посмотрим на отрицательную корреляцию между X и Y:
На приведенном выше рисунке большая часть X и Y распределена в областях II и IV, и только небольшая часть распределена в областях I и III.
Точно так же в регионах I и III (X-EX) (Y-EY)> 0; в областях II и IV (X-EX) (Y-EY) E ( X − E X ) ( Y − E Y ) 0 E(X-EX)(Y-EY) E ( X − E X ) ( Y − E Y ) 0
Приведенная выше формула означает, что математическое ожидание (X-EX) (Y-EY) меньше нуля, то есть среднее значение (X-EX) (Y-EY) меньше нуля.
Наконец, давайте посмотрим на ситуацию, когда X и Y не связаны:
На приведенном выше рисунке X и Y примерно равномерно распределены в областях I, II, III и IV.
Точно так же в регионах I и III (X-EX) (Y-EY)> 0; в областях II и IV (X-EX) (Y-EY) E ( X − E X ) ( Y − E Y ) = 0 E(X-EX)(Y-EY)=0 E ( X − E X ) ( Y − E Y ) = 0
Приведенная выше формула означает, что математическое ожидание (X-EX) (Y-EY) равно нулю, то есть среднее значение (X-EX) (Y-EY) равно нулю.
В итоге можно сделать следующие выводы:
Когда X и Y положительно коррелируют: E ( X − E X ) ( Y − E Y ) > 0 E(X-EX)(Y-EY)>0 E ( X − E X ) ( Y − E Y ) > 0
Когда X и Y отрицательно коррелируют: E ( X − E X ) ( Y − E Y ) 0 E(X-EX)(Y-EY) E ( X − E X ) ( Y − E Y ) 0
Когда X и Y не связаны: E ( X − E X ) ( Y − E Y ) = 0 E(X-EX)(Y-EY)=0 E ( X − E X ) ( Y − E Y ) = 0
Поэтому мы ввели понятие ковариации, которая представляет собой числовую характеристику, которая выражает взаимосвязь между X и Y. Мы определяем ковариацию как:
По результатам предыдущего обсуждения,
Когда Cov (X, Y)> 0, X и Y положительно коррелируют;
Здесь причиной деления на N-1 вместо N является объективная оценка общего ожидания выборки. Кстати, если Y = X, то ковариация представляет собой дисперсию X.
Ниже мы вычисляем ковариацию X и Y в трех вышеупомянутых случаях соответственно по формуле ковариации.
Когда X и Y положительно коррелированы, Cov (X, Y) = 37,3684;
2. Какая связь между коэффициентом корреляции и ковариацией?
Мы уже знаем, что такое ковариация и откуда берется формула ковариации. Если мы знаем взаимосвязь между ковариацией двух переменных X и Y и нуля, мы можем сделать вывод, являются ли X и Y коррелированными положительно, отрицательно или некоррелированными. Тогда возникает вопрос: отражает ли величина ковариации степень корреляции? То есть, если ковариация равна 100, обязательно ли она сильнее, чем положительная корреляция с ковариацией 10?
Взгляните на пример ниже!
Переменные X1 и Y1:
X1 = [11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]
Y1 = [12 12 13 15 16 16 17 19 21 22 22 23 23 26 25 28 29 29 31 32]
Переменные X2 и Y2:
X2 = [110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 260 270 280 290 300]
Y2 = [113 172 202 206 180 184 242 180 256 209 288 255 240 278 319 322 345 289 333 372]
Диаграммы совместного распределения X1, Y1 и X2, Y2 следующие:
Очевидно, из рисунка видно, что X1, Y1 и X2, Y2 все положительно коррелируют, и степень положительной корреляции между X1 и Y1, очевидно, больше, чем у X2 и Y2. Затем мы вычисляем ковариацию двух графиков, чтобы увидеть, так ли это.
авария! Ковариация X2 и Y2 в 100 раз больше, чем ковариация X1 и Y1. Не похоже, что чем больше ковариация, тем выше степень положительной корреляции. Это, в конце концов, почему?
Фактически, причина такой ситуации в том, что величины числовых изменений в двух ситуациях различаются (или различаются размеры). При вычислении ковариации мы не учитывали разницу в амплитуде различных переменных, и не существует единого стандарта измерения при сравнении ковариации.
Следовательно, чтобы устранить этот эффект, чтобы точно получить степень сходства между переменными, нам необходимо разделить ковариацию на стандартное отклонение соответствующих переменных. Таким образом получается выражение коэффициента корреляции:
Можно видеть, что коэффициент корреляции делится на стандартное отклонение переменных X и Y на основе ковариации. Формула для расчета стандартного отклонения:
Почему деление на стандартное отклонение соответствующих переменных устраняет влияние амплитуды? Это связано с тем, что само стандартное отклонение отражает степень изменения амплитуды переменной.Деление на стандартное отклонение может просто компенсировать его и стандартизировать ковариацию. Таким образом, диапазон коэффициента корреляции нормализуется до [-1,1].
Затем мы вычислим коэффициенты корреляции X1, Y1 и X2, Y2 в приведенном выше примере.
Итак, мы получаем, что коэффициент корреляции между X1 и Y1 больше, чем коэффициент корреляции между X2 и Y2. Это соответствует реальной ситуации. Другими словами, исходя из коэффициента корреляции, мы можем определить степень корреляции между двумя переменными и сделать следующие выводы:
Коэффициент корреляции больше нуля, это означает, что две переменные положительно коррелированы, и чем больше коэффициент корреляции, тем выше положительная корреляция;
Коэффициент корреляции меньше нуля, это означает, что две переменные имеют отрицательную корреляцию, и чем меньше коэффициент корреляции, тем выше отрицательная корреляция;
Коэффициент корреляции равен нулю, что означает, что две переменные не коррелированы.
Как бы вы объяснили разницу между корреляцией и ковариацией?
Подобно упомянутому вопросу, предпочтение отдается отсутствию формул.
Проблема с ковариациями заключается в том, что их трудно сравнивать: когда вы вычисляете ковариацию набора высот и весов, выраженную в (соответственно) метрах и килограммах, вы получите другую ковариацию, чем когда вы делаете это в других единицах ( что уже создает проблему для людей, делающих то же самое с метрической системой или без нее!), но также будет трудно сказать, если (например) рост и вес «больше равняются», чем, скажем, длина пальцев рук и ног просто потому, что «масштаб», на котором рассчитана ковариация, отличается.
Примечание: вышеизложенное предполагает, что читатель уже понимает понятие ковариации.
Требования этих типов вопросов кажутся мне немного странными. Вот математическая концепция / формула, но я хочу поговорить об этом в некотором контексте, полностью лишенном математических символов. Я также думаю, что следует заявить, что фактическая алгебра, необходимая для понимания формул, я думаю, должна преподаваться большинству людей до высшего образования (не требуется понимания матричной алгебры, достаточно простой алгебры).
Итак, сначала вместо того, чтобы полностью игнорировать формулу и говорить о ней в некоторых магических и эвристических аналогиях, давайте просто посмотрим на формулу и попытаемся объяснить отдельные компоненты небольшими шагами. Разница в терминах ковариации и корреляции при взгляде на формулы должна стать очевидной. Принимая во внимание, что если говорить с точки зрения аналогий и эвристики, я подозреваю, что эти два относительно простых понятия и их различия во многих ситуациях будут скрыты.
Итак, давайте начнем с формулы для выборочной ковариации (это я только что взял и принял из википедии);
1 n − 1 ∑ i = 1 n ( x i − x ¯ ) ( y i − y ¯ ) ‘ role=»presentation»> 1 n − 1 ∑ i = 1 n ( x i − x ¯ ) ( y i − y ¯ )
Чтобы ускорить процесс, давайте четко определим все элементы и операции в формуле.
На этом этапе я мог бы представить простой пример, чтобы, так сказать, взглянуть на элементы и операции. Так, например, давайте просто составим таблицу, в которой каждая строка соответствует наблюдению (а и помечены соответствующим образом). Вероятно, можно было бы сделать эти примеры более конкретными (например, скажем, представляет возраст, а представляет вес), но для нашего обсуждения здесь это не имеет значения. x ‘ role=»presentation»> x y ‘ role=»presentation»> y x ‘ role=»presentation»> x y ‘ role=»presentation»> y
Обратите внимание на то, что происходит при умножении, если два наблюдения оба находятся на большом расстоянии выше среднего, результирующее наблюдение будет иметь еще большее положительное значение (то же самое верно, если оба наблюдения находятся на большом расстоянии ниже среднего, так как умножение двух негативов равно положительному). Также обратите внимание, что если одно наблюдение намного выше среднего, а другое значительно ниже среднего, результирующее значение будет большим (в абсолютном выражении) и отрицательным (в положительное время отрицательное равно отрицательному числу). В заключение отметим, что когда значение очень близко к среднему для любого наблюдения, умножение двух значений приведет к небольшому числу. Опять же, мы можем просто представить эту операцию в виде таблицы.
В этот момент вы можете уточнить, откуда исходит 5, но это должно быть так же просто, как вернуться к таблице и подсчитать количество наблюдений (давайте снова оставим разницу между выборкой и популяцией в другое время).
Корреляция и Ковариация
Линейная корреляционная связь
Таких статистических связей может быть очень много самых разных. Для трейдера самым важным видом статистической связи является корреляционная связь.
Корреляционная связь, это когда каждому значению одной переменной соответствует определенное математическое ожидание другой переменной. То есть при изменении значения одной переменной, математическое ожидание другой переменной меняется закономерным образом.
А если при изменении значения одной переменной, закономерным образом меняется не только матожидание второй переменной, но и другие характеристики плотности распределения второй переменной (например, дисперсия, асимметрия и т.д.), то такая связь не является корреляционной. Хотя такая связь тоже является статистической.
Корреляционная связь между случайными переменными x и y называется линейной корреляционной связью, если матожидание переменной y линейно зависит от значений переменной x, и, одновременно, матожидание переменной x тоже линейно зависит от значений переменной y. То есть такая взаимная линейность корреляционных связей. Далее здесь рассматривается только линейная корреляционная связь.
Ковариация
Для независимых случайных величин X и Y всегда матожидание произведения случайных величин равно произведению их матожиданий по отдельности:
А для зависимых случайных величин это равенство не выполняется.
Ковариация, это отклонение математического ожидания произведения двух случайных величин от произведения их математических ожиданий:
Ковариация характеризует отклонение матожидания произведения двух случайных величин от произведения матожиданий этих величин. Так как это отклонение бывает только для зависимых величин, то ковариация характеризует степень этой зависимости. Чем она больше отличается от нуля, тем больше зависимость.
Коэффициент линейной корреляции
Ковариация неудобна тем, что имеет размерность квадрата случайных величин. Кроме того, ковариация маленькой статистической зависимости двух случайных величин с большой дисперсией (у хотя бы одной из этих величин) получается такой же, как большая статистическая зависимость у двух других случайных величин с маленькими дисперсиями. Поэтому ковариацию удобно нормировать на среднеквадратичные отклонения.
Коэффициент корреляции, это ковариация, нормированная на среднеквадратичные отклонения двух случайных величин.
Примеры
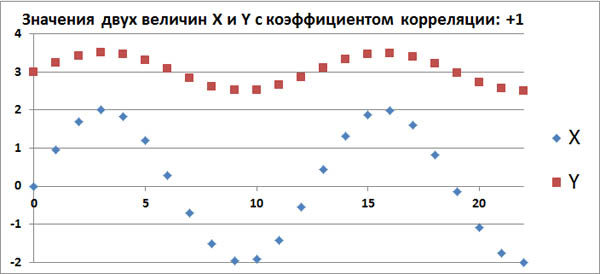
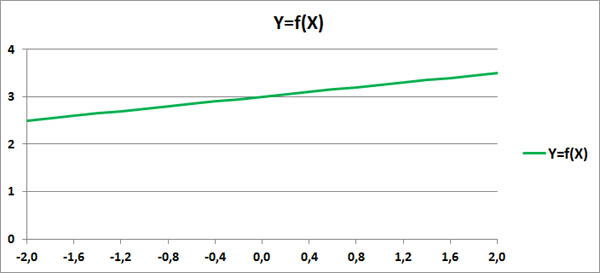
Допустим, в каком-то эксперименте в равные промежутки времени измеряют две величины, X и Y. Если их значения меняются, как на этом графике, то это полностью коррелированные величины с коэффициентом корреляции, равным +1.
Этот факт говорит о том, что между величинами X и Y имеется строгая функциональная зависимость: Y=f(X).
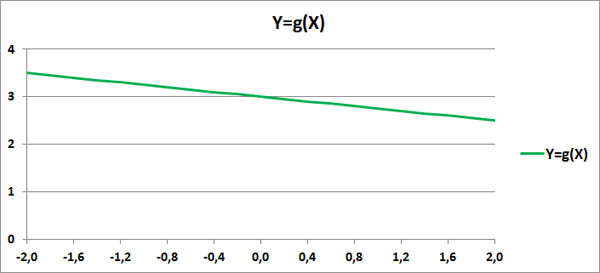
Этот факт также говорит о том, что между величинами X и Y имеется какая-то строгая функциональная зависимость: Y=g(X).
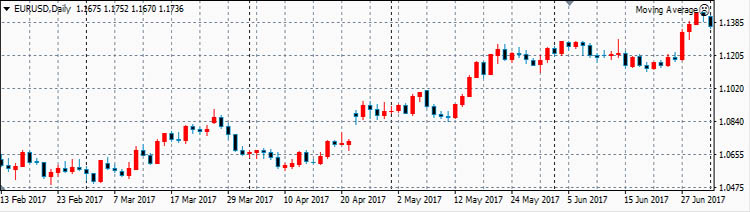
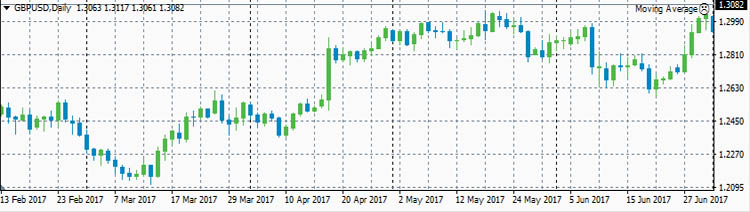
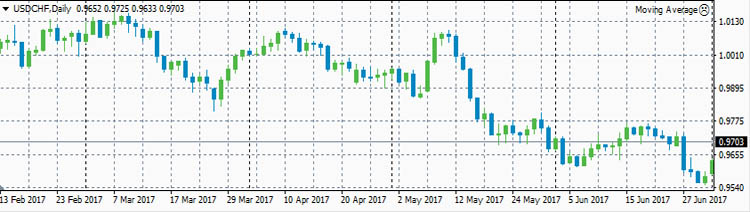
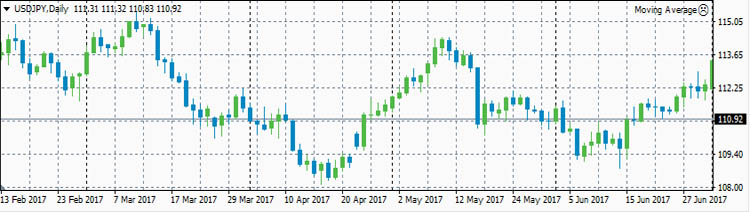
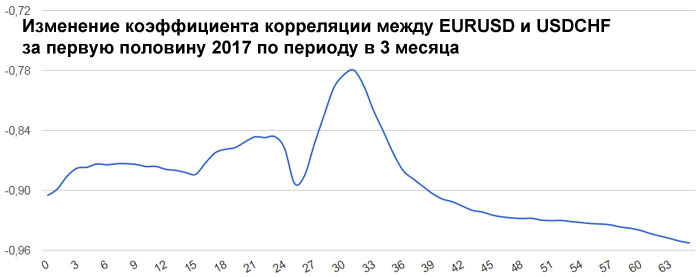
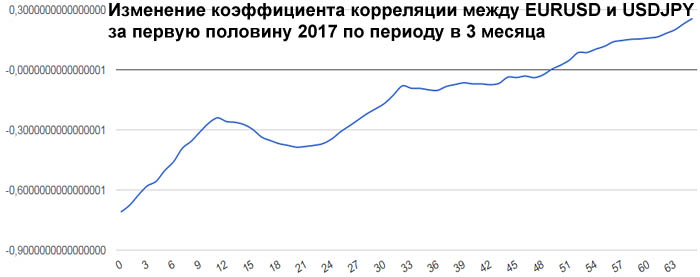
Теперь рассмотрим реальные цены. Для примера рассмотрим коэффициенты корреляции между ценами валютной пары EURUSD и ценами валютных пар GBPUSD, USDCHF и USDJPY. Для расчета возьмем дневные графики за первую половину 2017 года.
Эти коэффициенты корреляции достаточно ожидаемые.
Достаточно сильная корреляция между EURUSD и GBPUSD объясняется достаточно сильными связями экономики ЕвроЗоны и экономики Британии. Очень сильная антикорреляция между EURUSD и USDCHF объясняется еще более сильной связью между экономиками ЕвроЗоны и Швейцарии. А знак минус получился потому что в валютной паре USDCHF швейцарский франк стоит в знаменателе, в то время как в валютной паре EURUSD евро стоит в числителе.
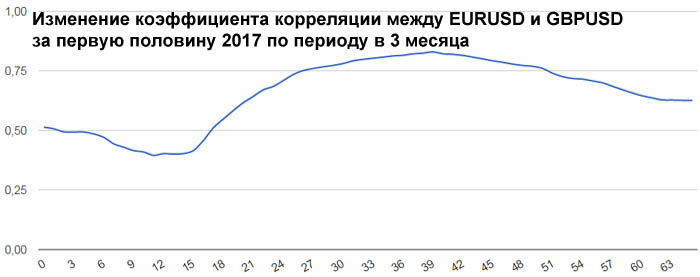
Интересно посмотреть не только коэффициенты корреляции разных валютных пар, но и то, как эти коэффициенты изменяются со временем. Для этого возьмем внутри полугодового периода трехмесячный период и посмотрим, как меняется коэффициент корреляции, если сдвигать этот трехмесячный период от начала полугодового периода до его конца. Всего за полгода будет 65 таких сдвижек.
В начале 2017 года корреляция между EURUSD и GBPUSD была небольшой и она даже немного уменьшалась. Но в середине полугодия корреляция между евро и фунтом усилилась. Таким образом, в определенное время фунт может не слишком хорошо коррелировать с евро.