в чем разница между дифракцией и интерференцией

Что такое интерференция и дифракция?

Разглядывая сияющее голографическое изображение, большинство из нас вряд ли вспоминает физические термины «дифракция» и «интерференция световых волн».

Но именно благодаря изучению этих понятий появилась возможность создавать голограммы.

Что такое дифракция света?

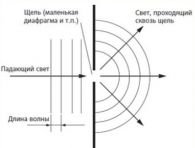
Слово «дифракция» образовано от латинского «diffractus», что означает в дословном переводе «огибание волнами препятствия». Как известно, свет имеет волновую природу, и его лучи подчиняются волновым законам. Дифракцией в физике называют оптические явления, возникающие, когда световые волны распространяются в оптически неоднородной среде с непрозрачными включениями.

Волновая природа света определяет его поведение при огибании препятствий. Если препятствие во много раз больше длины световой волны, свет не огибает его, образуя зону тени. Но в случаях, когда размеры препятствий соразмерны с длиной волны, возникает явление дифракции. В принципе, любое отклонение от геометрических оптических законов можно отнести к дифракции.

Интерференция волн

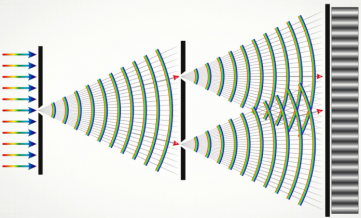
Если мы установим перед источником света непрозрачный экран и проделаем в нём точечное отверстие, то проникающие через эту точку лучи света на следующем экране, расположенном параллельно первому, отобразятся в виде концентрических колец с чередованием светлых и тёмных окружностей. Это явление в физике называют дифракцией Френеля, по имени учёного, который впервые обнаружил его и описал.

Изменив форму отверстия и сделав его щелеобразным, мы получим на втором экране другую картину. Световые лучи расположатся в виде ряда светлых и тёмных полосок, как на магазинном штрих-коде. Дифракцию света на щелеобразном отверстии впервые описал немецкий физик Фраунгофер, именем которого она называется до сих пор.

Объяснить разложение световой волны на светлые и тёмные участки учёные смогли при помощи понятия интерференции. Несколько источников волновых колебаний, если частоты их колебаний когерентны (одинаковы либо кратны друг другу), могут усиливать излучение друг друга, но могут и ослаблять, в зависимости от совпадения фаз колебаний. При огибании препятствий и возникновении вторичных волн вступает в действие их интерференция. На участках, где фазы волн совпадают, наблюдается повышенная освещённость (яркие светлые полоски либо окружности), а там, где не совпадают – освещённость снижена (тёмные участки).

Дифракционная решётка

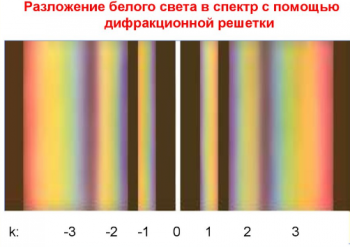
Если взять прозрачную пластинку и нанести на неё ряд параллельных непрозрачных чёрточек на одинаковом расстоянии друг от друга, то мы получим дифракционную решётку. При пропускании через неё плоского светового фронта образуется дифракция на непрозрачных штрихах. Вторичные волны, взаимно ослабляясь и усиливаясь, образуют дифракционные минимумы и максимумы, что легко обнаружить на экране, поставленном за решёткой.

При этом происходит не только отклонение световых лучей, но и разложение белого света на цветовые спектральные составляющие. В природе нужная для маскировки окраска крыльев бабочек, оперения птиц, змеиной чешуи часто образуется благодаря использованию дифракционных и интерференционных оптических явлений, а не из-за пигментов.

Голограммы

Принцип голограммы был изобретён в 1947 году физиком Д. Габором, который впоследствии получил за его изобретение Нобелевскую премию. Трёхмерное, т.е. объёмное изображение объекта можно снять и записать, а затем воспроизвести, если использовать лазерные лучи. Одна из световых волн называется опорной и испускается источником, а вторая – объектной и отражается от записываемого объекта.

На фотопластинке либо другом материале, предназначенном для записи, фиксируется сочетание светлых и тёмных полос и пятен, которые отображают интерференцию электромагнитных волн в этой зоне пространства. Если на фотопластинку направляют свет с длиной волны, соответствующей характеристикам опорной волны, то происходит его преобразование в световую волну, по характеристикам близкую к объектной. Таким образом, в световом потоке получается объёмное изображение зафиксированного объекта.

Сегодня неподвижные голограммы можно записывать и воспроизводить даже в домашних условиях. Для этого нужен лазерный луч, фотопластина и каркас, который надёжно удерживает в неподвижности эти приспособления, а также объект записи. Для домашней голограммы отлично подойдёт луч лазерной указки со снятой фокусирующей линзой.

Источник

Дифракция света

теория по физике 🧲 оптика

Дифракция — явление, присущее всем волновым процессам подобно интерференции. Чтобы лучше понять, в чем заключается явление дифракции света, сначала рассмотрим дифракцию механических волн.

Дифракция механических волн

Иногда на пути волны встречаются препятствия разных размеров. Если препятствия небольшие, волны легко их огибают и смыкаются за ними. Поэтому морские волны свободно огибают выглядывающие из воды камни и распространяются за ними так, как если бы их не было совсем. Если размер препятствия больше длины волны, за ним образуется «тень» — область, в которую волны проникнуть не могут.

На рисунке ниже видно, что за мелкими камнями волны распространяются так же, как если бы их не было. Но за большой глыбой поверхность воды спокойная — волны в эту область не проникают.

Внимание! Малыми препятствиями будем считать те, размеры которых намного меньше длины распространяющейся волны или сравнимы с ней.

Способность волн огибать препятствия является следствием отклонения распространения волн от их прямолинейного распространения. Такой способностью обладают не только волны на поверхности воды, но и звуковые волны. Вы услышите, как сигналит автомобиль за домом, который стоит между ним и вами препятствием именно благодаря дифракции. Звуковая волна обогнет дом и продолжит распространяться за ним. По этой же причине в лесу так далеко распространяется клик «Ау!» — деревья для звуковой волны не являются серьезным препятствием, и она их легко огибает.

Дифракция — явление отклонения от прямолинейного распространения волн.

Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней. Это явление встречается в природе, но его также можно вызвать искусственно. К примеру, дифракцию волн на поверхности воды можно наблюдать, налив воду в ванночку и поставив на пути возбуждаемых волн искусственное препятствие.

Если на пути распространения волн поставить экран с узкой щелью, размеры которой меньше длины волны, то увидим, что за ней начинает распространяться круговая волна. Такая же волна получилась, если бы в щели экрана находилось колеблющееся тело — источник волн.

Если же на пути распространения волны поставить экран с широкой щелью, за ним будет распространяться волна почти такой же формы. Волновая поверхность в этом случае искривляется только по краям щели.

Понять, почему появляется явление дифракции волн, помогает принцип Гюйгенса. Согласно ему, каждая точка волновой поверхности является источником вторичных волн. Вторичные волны, испускаемые участками среды, проникают за края препятствия, расположенного на пути распространения волны.

Дифракция световых волн

Если свет — это волна, то ему тоже должно быть присуще явление дифракции. Однако наблюдать дифракцию света сложно. Ведь дифракцию можно наблюдать тогда, когда препятствие сравнимо с длиной волны или меньше ее. А длина световой волны очень мала. Поэтому чтобы наблюдать дифракцию света, нужны очень малые препятствия.

Дифракция света на узкой щели

Наблюдать отклонение от прямолинейного распространения света можно, если пропустить пучок световых волн через узкую щель. При этом светлое пятно на экране будет больше, чем сама щель. Это возможно только в случае, если свет отклоняется от своего прямолинейного распространения.

Опыт Юнга

В 1802 г. Т. Юнг, который открыл интерференцию света, поставил классический опыт по наблюдению дифракции. В непрозрачной ширме он проколол булавкой два небольших отверстия В и С на малом расстоянии друг от друга. Эти отверстия он осветил узким световым пучком, прошедшим через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, определила успех эксперимента. Интерферируют ведь только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А вызвала в отверстиях В и С образование когерентных источников световых волн. Вследствие дифракции от отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции этих двух световых волн на экране появлялись картина, состоящая из чередующихся светлых и темных полос.

Закрыв одно из отверстий, Юнг обнаружил, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые ученый измерил длины волн, соответствующие световым лучам разного цвета. И ему удалось сделать это с высокой точностью.

Принцип Гюйгенса — Френеля

Исследование дифракции завершил французский ученый О. Френель. Он занимался детальным исследованием различных случаев дифракции, что позволило ему разработать количественную теорию дифракции. Она помогла физику получить точные расчеты дифракционной картины, которая возникала при огибании светом различных препятствий. Френелю также удалось впервые объяснить, почему в однородной среде свет распространяется прямолинейно.

Успех Френеля объясняется тем, что он стал первым, кто решил объединить принцип Гюйгенса с идеей интерференции вторичных волн. В результате зародилась теория, которая получила название принципа Гюйгенса — Френеля:

Волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.

Чтобы вычислить амплитуду световой волны в любой точке пространства, необходимо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду колебаний в рассматриваемой точке пространства. Такие расчеты дали объяснение тому, как свет от точечного источника S, являющегося источником сферических волн, достигает любой точки В пространства.

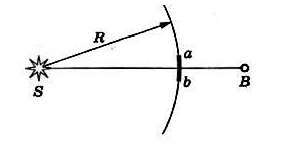
Если рассмотреть вторичные источники на сферической волновой поверхности радиусом R, то результат сложения вторичных волн от этих источников в точке В оказывается таким, как если бы только вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, распространяющие от источников, расположенных на остальной части поверхности, гасят друг друга в результате сложения. Поэтому все происходит так, как если бы свет распространялся вдоль прямой SB, т. е. прямолинейно. Эта теория Френеля доказала закон прямолинейного распространения света в однородной среде и позволила рассмотреть дифракцию с количественной точки зрения.

Внимание! Закон прямолинейного распространения света и другие законы геометрической оптики выполняются достаточно точно лишь в том случае, если размеры препятствий на пути распространения света много больше длины световой волны.

Дифракционные картины от различных препятствий

Расчеты Френеля получили экспериментальное подтверждение. Из-за малой длины световой волны угол ее отклонения от прямолинейного направления распространения небольшой. Поэтому наблюдать дифракцию можно только при использовании очень маленьких препятствий. Другой вариант наблюдения этого явления — расположение экрана вдали от препятствия.

Так, чтобы наблюдать дифракцию при расстоянии между экраном и препятствием в 1 м, размеры этого препятствия должны составлять сотые доли миллиметра. Если расстояние от препятствия до экрана увеличить до нескольких сотен метров, то размеры препятствия могут быть несколько сантиметров. Если расстояние между экраном и препятствием будет составлять несколько километров, дифракцию можно будет наблюдать при размерах препятствия в несколько метров.

Дифракционная картина — картина на экране, полученная в результате интерференции вторичных световых волн.

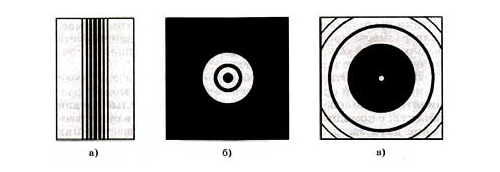
Подобную картину вы уже видели на картинке, иллюстрирующей опыт Юнга. Так, дифракционная картина от двух малых щелей — это чередующиеся темные и светлые полосы. Если использовать другие препятствия, картина будет меняться. На рисунке ниже схематично показаны дифракционные картины от различных препятствий: а — от тонкой проволочки; б — от круглого отверстия; в — от круглого экрана.

Вместо тени проволочка оставляет на экране светлые и темные полосы. В центре дифракционной картины, полученного от отверстия, появляется темное пятно, окруженное светлыми и темными кольцами. В центре тени, образованной круглым экраном, видно светлое пятнышко, а сама тень окружена темными кольцами. Если изменять диаметр отверстия, в центре дифракционной картины можно получить как светлое, так и темное пятно, окруженное либо темными, либо светлыми кольцами соответственно.

Дифракционная решетка

Дифракционная решетка — оптический прибор, принцип действия которого основан на явлении дифракции.

Дифракционная решетка представляет собой совокупность большого числа очень узких щелей, разделенных непрозрачными промежутками. Ее изготавливают путем нанесения на стекло штрихов. Их число может доходить до нескольких тысяч на 1 мм. Общее их число часто превышает 100 тысяч. Решетку также можно получить из металла, на котором чередуются участки, отражающие и рассеивающие свет.

Период дифракционной решетки равен сумме ширины прозрачных щелей и ширины непрозрачных промежутков:

Внимание! Обычно изготавливают дифракционные решетки с периодом в 10 мкм.

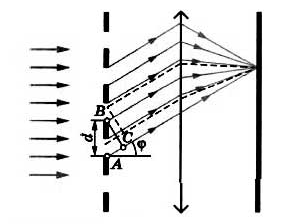
Пусть на дифракционную решетку с периодом d падает плоская монохроматическая волна, длина волны которой составляет λ.

При этом вторичные источники, расположенные в щелях решетки, создают световые волны, распространяющиеся по всем направлениям. Найдем условие, при котором идущие от щелей волны усиливают друг друга (складываются). Для этого рассмотрим волны, распространяющиеся в направлении под углом φ к дифракционной решетке.

Разность хода между волнами от краев соседних щелей равна длине отрезка АС. Если на этом отрезке вмещается целое число длин волн, то волны от всех щелей при сложении будут усиливать друг друга. Из треугольника АВС найдем длину катета АС:

При этом максимумы будут наблюдаться под углом φ в соответствии с условием:

где величина k = 0, 1, 2, … определяет порядок спектра.

Нужно учитывать, что при выполнении условия друг друга усиливают как волны, распространяющиеся от нижних краев щелей, так и волны, распространяющиеся от всех других точек щелей. Каждой точке в первой щели соответствует точка во второй щели, находящаяся на расстоянии d от первой точки. Поэтому разность хода испущенных этими точками вторичных волн равна kλ, и эти волны взаимно усиливаются.

Рассмотрим следующий случай. За решеткой поместим собирающую линзу, а за ней — экран на фокусном расстоянии от линзы. Линза фокусирует лучи, идущие параллельно, в одной точке (в фокусе). В этой точке волны складываются и взаимно усиливаются. Углы φ, удовлетворяющие условию, определяют положение так главных максимумов на экране (соответствующих 1, 2 и т.д. порядку).

Наряду с картиной, получаемой в результате дифракции света, в случае дифракционной решетки наблюдается дифракционная картина и от отдельных щелей. Интенсивности максимумов в ней меньше интенсивности главных максимумов. Так как положение максимумов (кроме центрального, соответствующего k = 0) зависит от длины волны, то решетка разлагает белый свет в спектр. Чем больше λ, тем дальше от центрального максимума располагается тот или иной максимум, соответствующий данной длине волны.

Каждому значению k соответствует свой порядок спектра. Между максимумами расположены минимумы освещенности. Чем больше число щелей, тем более резко очерчены максимумы и тем более широкими минимумами они разделены.

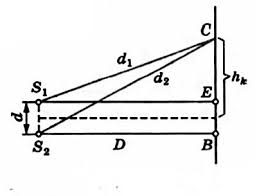
Пример №1. В опыте Юнга по дифракции расстояние между щелями равно d = 7∙10 –4 м. Расстояние от двойной щели до экрана равно D = 2 м. При освещении прибора зеленым светом расстояние между соседними светлыми дифракционными полосами оказалось равным ∆h = 16∙10 –2 м. Вычислите длину волны.

В некоторой точке С экрана будет наблюдаться максимум освещенности при выполнении условия:

где величина k = 0, 1, 2, … — целые числа.

Применим теорему Пифагора к треугольникам S₁CE и S_sCB:

Вычитая из первого равенства второе, получаем:

d 2 2 − d 2 1 = 2 h k d

( d 2 + d 1 ) ( d 2 − d 1 ) = 2 h k d

Так как расстояние между щелями много меньше расстояния между ними и экраном, то можем считать, что:

Отсюда можем найти расстояние k-той светлой полосы от центра экрана:

Расстояние между соседними полосами равно:

На плоскую непрозрачную пластину с узкими параллельными щелями падает по нормали плоская монохроматическая волна из красной части видимого спектра. За пластиной на параллельном ей экране наблюдается интерференционная картина, содержащая большое число полос. При переходе на монохроматический свет из синей части видимого спектра

а) расстояние между интерференционными полосами увеличится

б) расстояние между интерференционными полосами уменьшится

в) расстояние между интерференционными полосами не изменится

г) интерференционная картина станет невидимой для глаза

Алгоритм решения

Решение

Зависимость расстояния между интерференционными полосами от частоты световых лучей удалось установить экспериментально. Было выяснено, что чем выше частота, тем меньше расстояние между ними. Частота света из синего части спектра больше частоты из красной части спектра. Поэтому при переходе из красной части спектра в синюю часть расстояние между полосами интерференционной картины уменьшится.

pазбирался: Алиса Никитина | обсудить разбор | оценить

В прозрачном сосуде, заполненном водой, находится дифракционная решётка. Решётка освещается лучом света лазерной указки, падающим перпендикулярно её поверхности через боковую стенку сосуда. Как изменятся частота световой волны, длина волны, падающей на решётку, и угол между падающим лучом и первым дифракционным максимумом при удалении воды из сосуда?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Когда воды в сосуде не станет, изменится оптическая плотность среды — ею будет воздух, имеющий абсолютный показатель преломления 1 (у воды он равен 1,33).

Частота световой волны — величина постоянная. Она не меняется при изменении любых величин.

Длина световой волны меняется с учетом оптической плотности среды. Она определяется формулой:

В оптически более плотной среде скорость распространения волны уменьшается. Но когда их сосуда была удалена вода, оптическая плотность уменьшилась, значит, скорость волны увеличилась. Так как частота волны — постоянная, а длина волны прямо пропорциональна ее скорости, то при увеличении скорости длина волны тоже увеличится.

В оптически более плотной среде волны отклоняются от прямолинейного распространения сильнее в сторону нормали. Поэтому при удалении воды, когда оптическая среда станет менее плотной, лучи отклонятся от нормали. В этом случае угол между нормалью к решётке и первым дифракционным максимумом увеличится.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Дифракционная решётка с периодом 10 –5 м расположена параллельно экрану на расстоянии 0,75 м от него. На решётку по нормали к ней падает пучок света с длиной волны 0,4 мкм. Какого порядка максимум в спектре будет наблюдаться на экране на расстоянии 3 см от центра дифракционной картины? Считать sina ≈ tga.

Источник

В чем разница между дифракцией и интерференцией

В связи с тем, что раздел «Оптика» в школьном курсе физики является наиболее сложным, более глубокому усвоению и пониманию материала способствует решение задач и выполнение лабораторных работ.

Содержание курса «Оптика»

Экспериментальные факты: опыт Герца, опыт Юнга, кольца Ньютона и др.

Основные понятия: электромагнитные волны, когерентность, интерференция и дифракция света, оптическая разность хода, дисперсия и поглощение света; геометрическая оптика: световой луч, показатель преломления среды.

Законы и уравнения: законы отражения и преломления света, формула тонкой линзы, закон дисперсии, закон Малюса.

Выводы теории и их практическое применение: получение условий максимума и минимума при интерференции света, цвета тонких пленок, применение интерференции в технике: проверка качества обрабатываемой поверхности, просветление оптики, определение длины волны, использование дифракционной решетки в спектрографе для спектрального анализа, оптические приборы (лупа, микроскоп, телескоп) и их практическое применение.

Электромагнитные волны

В теме «Электромагнитные волны» должны быть, прежде всего, рассмотрены такие вопросы как понятие электромагнитных волн, их экспериментальное обнаружение, свойства электромагнитных волн, шкала электромагнитных волн.

1. Следует подчеркнуть, что существование электромагнитных волн было теоретически предсказано английским физиком Джеймсом Кларком Максвеллом. На основе своих уравнений он пришел к выводу, что в вакууме и диэлектриках произвольные возмущения электромагнитного поля распространяются в виде электромагнитной волны.

Максвелл показал, что скорость электромагнитных волн в диэлектриках равна:

Скорость электромагнитной волны в вакууме

2. Электромагнитная волна является поперечной, так как векторы (напряженность электрического поля) и (напряженность магнитного поля) перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис. 1).

3. Электромагнитные волны, как и другие волны, переносят энергию. Эта энергия заключена в распространяющихся электрическом и магнитном полях. Показано, что объемные плотности энергии электрического и магнитного полей:

Тогда плотность энергии электромагнитной волны:

Следует обратить внимание учащихся на то, что эта формула характеризует плотность энергии в любой момент времени в любой точке пространства.

Модули векторов электрического Е и магнитного Н у электромагнитной волны связаны соотношением:

Определим энергию, переносимую электромагнитной волной в единицу времени через единичную площадку (плотность потока энергии электромагнитного излучения). Вектор плотности электромагнитной энергии можно представить как векторное произведение и :

Вектор — вектор Пойтинга. Направление вектора совпадает с направлением переноса энергии, то есть совпадает с направлением распространения электромагнитной волны в вакууме.

4. Электромагнитная волна должна обладать импульсом, а поэтому оказывать давление на тела. Давление электромагнитной волны:

где — коэффициент отражения, — среднее значение плотности энергии.

Впервые опыты с электромагнитными волнами были осуществлены в 1888 г. Генрихом Герцем. Дальнейшие исследования электромагнитных волн показали, что они обладают способностью испытывать отражение, преломление, дифракцию, интерференцию и поляризацию.

На основании связи напряженностей магнитного Н и электрического поля Е имеем:

Магнитная индукция . Тогда, используя (1), имеем:

так как в вакууме

Величина среднего значения вектора Пойтинга , так как .

Отсюда

Подставляя численные значения, получим:

Ответ:

Как видно из этого примера, численное значение В очень мало по сравнению со значением Е.

Интерференция света

Рассмотрение вопросов волновой оптики очень важно для понимания физической сущности световых явлений. Наиболее отчетливо волновые свойства света проявляются в явлениях интерференции и дифракции.

В теме «Интерференция света» должны быть рассмотрены основные условия наблюдения интерференции света, способы получения когерентных источников в оптике, расчет интерференционной картины (опыт Юнга), интерференция в тонких пленках, практическое применение интерференции.

Следует подчеркнуть, что интерференционную картину невозможно получить с помощью обычных источников, например, электрических лампочек. Включение еще одной лампочки приводит к увеличению освещенности поверхности, а не к чередованию максимумов и минимумов освещенности. Это объясняется тем, что естественные источники света не когерентны. Интерферировать могут только когерентные волны.

Основная трудность в осуществлении интерференции света состоит в получении когерентных световых волн. Экспериментальные методы получения когерентных пучков из одного светового пучка можно разделить на два класса:

1) метод деления волнового фронта.

2) метод деления амплитуды.

В методе деления волнового фронта пучок света пропускается, например, через два близко расположенных отверстия в непрозрачном экране (опыт Юнга) (рис. 2).

Эти два отверстия бесконечно малого диаметра, расстояние между ними d > d, то Х >> , то есть интерференционные полосы хорошо различимы. Если L d, то X . Для световых волн, длины волн которых порядка долей микрона, интерференционные полосы неразличимы глазом и для их наблюдения используется микроскоп.

Следует обратить внимание на то, что положение максимума зависит от длины волны . Если в качестве источника света используется белый свет, то только нулевой (k = 0) максимум окажется белым, а все остальные максимумы будут окрашены.

Максимумы для коротких (фиолетовых) длин волн будут расположены ближе к нулевому максимуму, чем максимумы для больших длин волн (красных). Образующийся интерференционный спектр первого порядка будет обращен своей фиолетовой частью к середине экрана. Интерференционные спектры более высоких порядков могут значительно перекрывать друг друга.

Решение. Ширина интерференционной полосы . Поскольку при смене светофильтров L и d не изменялись, то

Таким образом, расстояние между соседними интерференционными полосами при замене зеленого светофильтра на красный увеличится в 1,3 раза.

Решение. В опыте Юнга две щели (точки А и В на рис. 3) являются когерентными источниками, дающими на экране интерференционную картину. Предположим, что эти источники точечные. Тогда интерференционная картина рассчитывается по формулам для максимума и минимума интенсивности. Сместим источники вверх на расстояние d₀. Интерференционная картина сместится также вверх на расстояние d₀. Рассмотрим суммарную интерференционную картину от четырех точечных источников, расположенных в точках А и А’, В и В’.

Она будет состоять из двух интерференционных картин, сдвинутых одна относительно другой на расстояние d₀. Если это расстояние меньше расстояния между соседними светлой и темной полосами, которое равно L/(2d), то суммарная интерференционная картина получится отчетливой.

Пусть теперь имеется два неточечных когерентных источника (щели шириной АА’ = ВВ’ = d₀ ). Согласно сказанному, суммарная интерференционная картина отчетлива, если выполняется условие , то есть

Ответ:

Далее следует указать, что интерференцию света можно наблюдать не только в лабораторных условиях (применяя для этого различные оптические установки), но и в повседневной жизни. Например, радужные переливы мыльных пузырей, тонких пленок нефти на поверхности воды, или пленок окислов, возникающих на поверхности металла при закалке.

Для объяснения этого явления необходимо рассмотреть плоскопараллельную пластинку с показателем преломления n, толщиной d, на которую падает плоская световая волна с длиной волны под углом к нормали к поверхности пластинки. При освещении пленки происходит наложение световых волн от одного и того же источника, отразившихся от передней и задней поверхностей тонкой пленки. Результат их интерференции зависит от оптической разности хода, приобретенной этими волнами.

Интерференционная картина, образованная отраженными под разными углами плоскими волнами от поверхностей плоскопараллельной пластинки, получила название интерференционных полос равного наклона.

Интерференция наблюдается не только в отраженном, но и в проходящем сквозь пленку свете, причем максимумам интерференции в отраженном свете соответствуют минимумы в проходящем свете, и наоборот.

В заключение следует обратить внимание учащихся на задачи по теме «Кольца Ньютона», которые отсутствуют в школьных задачниках.

где k = 1, 2. Полагая k = 1, 2…, получим ряд значений для длин волн ₁ = 682 нм, ₂ = 136,4 м и т.д.

Следует обратить внимание учащихся на то, что последующие значения ₂, ₃ и т.д. не соответствуют видимой области спектра.

Ответ: = 682 нм.

Пример 3. На поверхности стеклянной пластинки с показателем преломления n₁ = 1,2 нанесена пленка толщиной d = 150 нм с показателем преломления n₂ = 1,45. Для какой длины волны видимого света коэффициент отражения будет максимальным?

Решение. Для того чтобы коэффициент отражения был максимальным, необходимо, чтобы лучи отражения от верхней и нижней поверхностей пленки, нанесенной на стекло, усиливали друг друга. Это будет иметь место при условии:

Ответ: = 435 нм (сине-фиолетовый цвет).

Дифракция света

При рассмотрении явления дифракции света необходимо определить это явление, рассмотреть принцип Гюйгенса-Френеля, метод зон Френеля для объяснения дифракции сферической волны на круглом отверстии, дифракции в параллельных лучах и дифракционную решетку.

Качественное проникновение света в область геометрической тени можно объяснить с помощью принципа Гюйгенса. Однако принцип Гюйгенса не дает никаких указаний об интенсивности волн, распространяющихся в разных направлениях. Этот принцип, дополненный Френелем представлением об интерференции вторичных волн, получил название принципа Гюйгенса-Френеля. Для нахождения результата интерференции вторичных волн Френель предложил оригинальный метод деления волновой поверхности на зоны, так называемый метод зон Френеля (рис. 4). Способ построения зон Френеля достаточно прост. Расчеты показывают, что площади зон Френеля одинаковы, а колебание, возбуждаемое в точке наблюдения двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон равна . Тогда можно показать, что амплитуда колебания, создаваемого открытым фронтом сферической волны, равна половине амплитуды колебания, создаваемого одной центральной зоной Френеля (). Следовательно, можно считать, что в свободном пространстве свет распространяется прямолинейно, так как размеры зон для световой волны малы.

Следует обратить внимание учащихся на то, что с помощью зон Френеля решаются задачи о дифракции света на непрозрачном диске и другие более сложные задачи. Но данный метод является приближенным расчетным приемом, заменяющим строгое решение задачи о распространении света.

Пример. На круглое отверстие диаметром d = 3 мм падает нормально плоская монохроматическая световая волна (параллельный пучок). На расстоянии b = 0,6 м от отверстия расположен экран. Определите число зон Френеля, укладывающихся в отверстии. Длина световой волны = 0,6 мкм.

Решение. Число зон, укладывающихся в отверстии, получим, разделив площадь отверстия на площадь одной зоны:

Тогда площадь одной зоны .

Число зон .

Ответ: на экране укладывается примерно 6 зон (то есть наблюдается почти полное гашение света).

Дифракция Фраунгофера имеет место, когда на препятствие падает плоская волна, или параллельные лучи. Необходимо подчеркнуть, что наблюдение распределения интенсивности ведется там, где пересекаются параллельные дифрагированные лучи, то есть теоретически на бесконечности, а практически в фокальной плоскости линзы. Практический интерес представляет дифракция на большом количестве щелей, то есть на дифракционной решетке.

Дифракционная решетка используется для измерения длин световых волн, для анализа спектрального состава сложного излучения.

Рассмотрим пример. На дифракционную решетку нормально к ее поверхности падает монохроматический свет длиной волны = 0,45 мкм. Постоянная решетки d = 0,2 мкм. Определите, сколько максимумов дает дифракционная решетка.

Условие главного максимума . Отсюда

В заключение следует обратить внимание на тот факт, что между дифракцией и интерференцией нет принципиального различия. Оба этих явления заключаются в перераспределении светового потока при суперпозиции (наложении) когерентных волн. По историческим причинам мы говорим об интерференции, когда речь идет о перераспределении интенсивности в результате суперпозиции волн, возбуждаемых конечным (обычно небольшим) числом когерентных источников. Перераспределение интенсивности, возникшее при суперпозиции волн когерентных источников, расположенных непрерывно, принято называть дифракцией.

Дисперсия и поглощение света

Если свет проходит через стеклянную призму, то выходящий пучок света не будет параллелен падающему, а отклонится на некоторый угол от первоначального направления. На экране появятся окрашенные полосы, от красного до фиолетового цвета. Впервые разложение белого света в спектр было получено И. Ньютоном еще в 1666 г. Эти опыты показали, что фиолетовые лучи отклоняются от первоначального направления сильнее, чем красные.

Следует подчеркнуть, что этот закон фактически справедлив только для газов, так как при выводе не учитывалось взаимодействие между молекулами. Однако для качественного объяснения явления дисперсии его можно использовать и для жидкостей, и для твердых тел.

Далее рассматривается явление поглощения света и его качественное объяснение с помощью упрощенной электронной теории. Подчеркивается, что под действием внешнего электромагнитного поля электроны в атомах совершают вынужденные колебания. Если частота этой электромагнитной (световой) волны совпадает с частотой собственных колебаний электрона, то, как известно из теории колебаний, возникает явление резонанса. Оно и обусловливает поглощение света. Рассмотрите графическую зависимость коэффициента поглощения от длины волны. Следует обратить внимание учащихся на то, что максимально поглощаются световые волны в области аномальной дисперсии. Подробно механизм поглощения света атомами и молекулами рассматривается в квантовой механике, что выходит за рамки школьного курса.

В заключение следует отметить, что цвет тела (не самосветящегося) зависит не только от его оптических свойств, но и от того, каким светом оно освещается. Так, например, если данное тело способно отражать только лучи красного цвета, то при освещении его зелеными лучами оно будет казаться нам просто черным. Если же это тело освещать белым светом, то оно отражает красные лучи, входящие в состав белого света и будет казаться нам красным.

Объясните, какого цвета будет видеть наблюдатель лист красной бумаги при освещении его: 1) белым светом; 2) белым светом, но смотреть на него наблюдатель будет через а) красный светофильтр, б) зеленый светофильтр.

Поляризация света

При изучении явлений интерференции и дифракции света вопрос о том, являются ли световые волны продольными или поперечными, не имел значения. Однако существуют процессы, в которых проявляется различие между поперечными и продольными волнами.

Из электромагнитной теории света следует, что свет представляет собой поперечную волну, то есть векторы . Следует обратить внимание учащихся на то, что обычные источники света (солнце, лампа накаливания, фонарь и т.п.) испускают свет, в котором электрический вектор совершает колебание в самых разных направлениях в плоскости, перпендикулярной к скорости распространения волны. Такой свет называется естественным или неполяризованным.

Поляризованным, в отличие от естественного света, называется свет, в котором направление колебаний электрического вектора сохраняется неизменным.

Необходимо рассмотреть способы получения поляризованного света из естественного. Одним из таких способов является прохождение света через кристалл турмалина. Турмалин обладает свойством дихроизма: пропускает лучи, электрический вектор которых параллелен оптической оси, поглощая лучи, у которых электрический вектор перпендикулярен к оптической оси турмалина. Поэтому естественный свет, пройдя через пластинку турмалина, становится линейно поляризованным.

Далее рассматриваются две прямоугольные пластинки из турмалина, вырезанные так, что одна из сторон прямоугольника совпадает с оптической осью кристалла. В зависимости от того, как ориентированы друг относительно друга обе пластинки, меняется интенсивность прошедшего через них света. Первая пластина турмалина переводит естественный свет в линейно поляризованный (поляризатор), а вторая анализирует полученные колебания (анализатор).

При повороте одной из пластин турмалина на 360 o интенсивность пучка, прошедшего через обе пластинки, два раза достигает максимума и два раза проходит через минимум. Математически этот результат был описан Малюсом:

то есть . Таким образом, после прохождения света через два поляроида интенсивность его уменьшилась в восемь раз.

Отметим, что поляризация света наблюдается и в других случаях, например, при отражении и преломлении света на границе двух диэлектриков.

В заключение подчеркнем, что интерференция и дифракция наблюдаются с волнами любой природы и, что важно, как с продольными, так и поперечными. Поляризация же является отличительной чертой именно поперечных волн.

Геометрическая оптика

Все задачи оптики можно решить на основе волнового представления, но это требует применения громоздкого математического аппарата. Однако задолго до того, как были выяснены волновые свойства света, ученые пользовались геометрическими методами решения задач на построение изображений в зеркалах и линзах, при расчете оптических приборов.

Геометрическая оптика базируется на трех законах: законе прямолинейного распространения света, законе независимости световых лучей, законах отражения и преломления света. Основным понятием геометрической оптики является световой луч. Под световым лучом понимается линия, указывающая направление распространения световой энергии. Обратите внимание, что это не физическая модель, а чисто геометрическое понятие, облегчающее решение оптических задач методами геометрической оптики.

Далее излагается принцип Ферма, сформулированный еще в 1660 г. французским ученым П. Ферма, и показывается, что основные законы геометрической оптики можно получить, используя лишь принцип Ферма и предположение о постоянстве скорости света в однородной среде.

Обратить внимание учащихся на формулу тонкой линзы в такой записи:

Целесообразно поставить перед школьниками вопрос: можно ли с помощью двояковогнутой линзы получить действительное изображение предмета?

Оптические приборы

Говоря об оптических приборах, надо прежде всего проанализировать работу глаза, его строение. Далее необходимо подчеркнуть, что глаз должен одинаково хорошо видеть предметы, расположенные на разных расстояниях от него. На сетчатке должно получится четкое изображение при изменении расстояния d от предмета до глаза. Это возможно только в том случае, если одновременно меняется фокусное расстояние оптической системы. Как следует из формулы тонкой линзы, это происходит за счет радиусов кривизны поверхности хрусталика. Это явление называется аккомодацией.

Размер изображения предмета на сетчатке h определяется углом зрения с вершиной в оптическом центре глаза и лучами, направленными на крайние точки предмета. Угол зрения можно увеличить, приблизив предмет к глазу, но при этом глаз устает. Далее вводится понятие расстояния наилучшего зрения. Возрастание изображения ограничено расстоянием наилучшего зрения (

25 см для нормального глаза).

Телескоп служит для увеличения угла зрения при рассмотрении удаленных предметов, например, планет, звезд.

В заключение следует рассмотреть понятие разрешающей способности оптических приборов (телескопа, микроскопа), подчеркнуть, что дифракция света накладывает ограничения на разрешающую способность этих приборов.

Источник