в чем разница между диаметром и радиусом
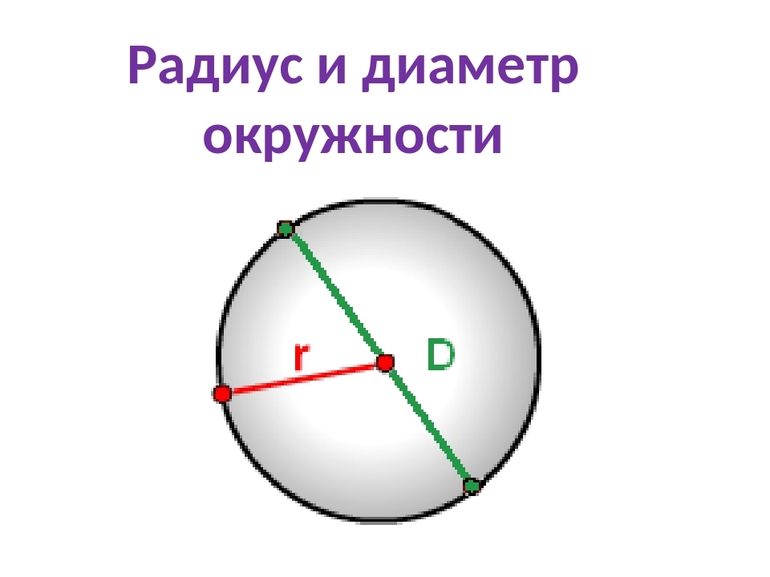
Разница между радиусом и диаметром
Окружность представляет собой кривую линию, которая образована из всех точек, равноудаленных от одной определенной точки, которую называют центром окружности. По-другому можно дать такое определение окружности: кривая, которая замкнута на плоскости, и все точки которой, лежащие в той же плоскости, что и кривая, удалены от центра на одинаковое расстояние. Каждая точка окружности находится от центра окружности на одинаковом расстоянии.
Определение
Радиус — это отрезок прямой, который соединяет каждую точку окружности, которая находится на равном расстоянии от центра окружности, с центром окружности.
Диаметр — это отрезок прямой линии, который соединяет любые две удаленные друг от друга точки окружности и всегда должен проходить через центр этой окружности.
Сравнение
Радиусом называют отрезок прямой, который соединяет каждую точку окружности, которая находится на равном расстоянии от центра окружности, с центром окружности. Радиус обозначают буквой R. Он показывает длину этого отрезка. Центр окружности обозначается буквой O.
Диаметром называют отрезок прямой, который всегда должен проходить через центр окружности, и соединять две любые удаленные друг от друга точки окружности. Любой такой отрезок прямой называют диаметром и обозначают буквой D. Длину диаметра также обозначают буквой D.
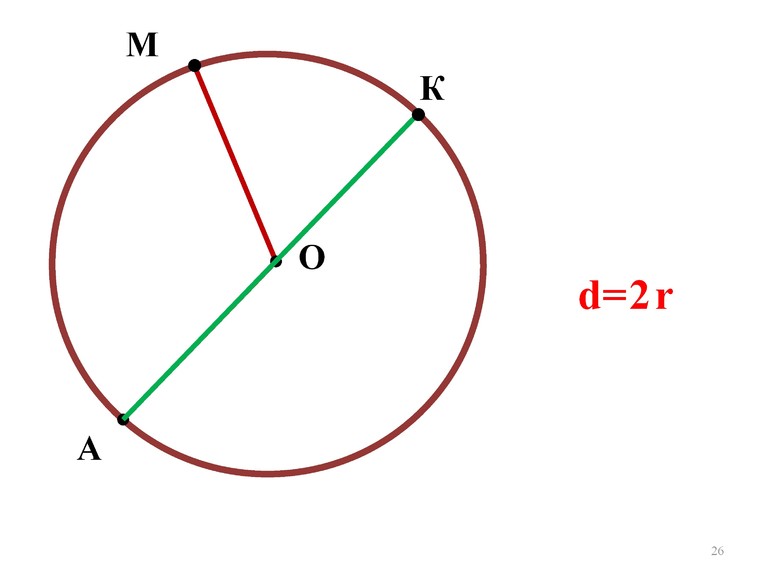
Пусть точки A, B находятся на самой окружности, тогда отрезки OA, OB — это радиусы этой окружности.
Их длины равны: OB=OA.
Диаметр будет равняться двум радиусам. D = 2R. Соответственно, радиус будет равняться половине диаметра: R = D/2.
что такое радиус и диаметр?
Свернуть
WLE Austria Logo (no text).svgФотоконкурс «Вики любит Землю»: Ваш взгляд на российские природные памятники!
Диаметр
[править | править вики-текст] Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 февраля 2016; проверки требуют 12 правок.
Диа́метр в изначальном значении термина — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.
Содержание [убрать]
1Диаметр геометрических фигур
2Символ диаметра
2.1Сопряжённые диаметры эллипса и гиперболы
2.2Сопряжённые диаметры эллипса
2.3Сопряжённые диаметры гиперболы
3Вариации и обобщения
4Некоторые окружности, построенные в треугольнике на одном отрезке, как на диаметре
5См. также
6Литература
Диаметр геометрических фигур [править | править вики-текст]
Радиус (r) и диаметр (d) окружности
Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.
Символ диаметра [править | править вики-текст]
Символы со сходным начертанием: Ø · ∅
Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как ⌀ или ⌀). Этот символ не присутствует в стандартных раскладках, поэтому для его ввода при компьютерном наборе необходимо использовать вспомогательные средства — например, приложение «Таблица символов» в Windows, программу «Таблица символов Юникода» (gucharmap) в GNOME, команду «Вставка» → «Символ…» в программах Microsoft Office и т. д. Специализированные программы могут предоставлять пользователю свои способы ввода этого символа: к примеру, в САПР AutoCAD для ввода символа диаметра используется сочетание символов %%c (буква c — латинская) или \U+2205 в текстовой строке.
Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.
Сопряжённые диаметры эллипса и гиперболы [править | править вики-текст]
Сопряжённые диаметры эллипса [править | править вики-текст]
Пара сопряжённых диаметров эллипса. Если в точках касания диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу и четыре таких касательных ко всем четырем концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм
Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
На рисунке представлена пара сопряженных диаметров (красный и синий). Если в точках касания диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу, и четыре таких касательных ко всем четырем концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм (зеленые линии на рисунке).
Расстояния r_1 и r_2 от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
Радиус эллипса в данной точке (расстояние от его
Радиус и диаметр окружности — определение двух отрезков
На практике в жизни с окружностью сталкивается каждый человек. Это может быть обруч, который крутят на уроке физкультуры либо на занятиях фитнеса, а также арена цирка либо просто украшение на пальце — кольцо. Радиус и диаметр окружности — взаимосвязанные математические понятия, которые необходимо выучить детям в школьной программе еще в начальной школе.
Определения понятий
Чтобы изобразить фигуру, достаточно обвести контур карандашом вокруг круглого предмета либо начертить при помощи циркуля. На месте прокола циркуля ставят точку, что и будет центром окружности.
Окружность — геометрическое место точек плоскости, в котором длина от точек к центру одинаковая. По-другому можно описать определение, что это замкнутая кривая, в которой править будут равные отрезки, проведенные от центра до краев фигуры. Круг — часть плоскости, которая ограничена окружностью.
Если поставить точку на окружности и соединить ее с центром, в результате получится отрезок. Таких отрезков можно нарисовать не один, сколько точек на окружности поставить — столько и будет таких отрезков, то есть бесчисленное количество.
Отрезок, который равен расстоянию от центра до границ окружности имеет название радиуса. Этот термин с латинскими корнями и в переводе означает луч либо спица колеса.
Первый раз о термине заговорили в 1569 году, и примерно через 100 лет он стал общепринятым. И не удивительно, так как в обиходе люди часто говорят, к примеру, «пожар в радиусе 10 км уничтожил все», «в радиусе 5 м нет видимости» и так далее.
Диаметром называется отрезок, который соединяет 2 точки окружности и проходит обязательно через центр круга. Такой отрезок делит круг на 2 части. По-другому — хорда, которая проходит через центр круга. Этот отрезок самый больший, который можно изобразить в круге, что и будет отличаться от других отрезков. Их можно изобразить в фигуре бесконечное число.
Обозначения и свойства
Понятия имеют принятые обозначения. Буквой d обозначают диаметр (в некоторых источниках обозначается перечеркнутой буквой о), а r — радиус. Для измерения используют:
Диаметр состоит из 2 радиусов, а это значит, если необходимо узнать, чему равен радиус, необходимо длину диаметра разделить напополам. То есть разница между ними в 2 раза. Не всегда два радиуса образуют диаметр: только при условии, если они находятся на одной прямой.
Для решений задач можно использовать формулу: d =2*r. Естественно, формула работает в обратном направлении, она будет выглядеть следующим образом: r = d/2.
Дано: r =80 мм, определить, на сколько сантиметров диаметр длиннее. Для решения задачи используют формулу d=2*r. Но для начала необходимо перевести миллиметры в сантиметры. 80 мм=8 см. Далее d=2*8=16 см. Чтобы вычислить отличие, необходимо 16−8=8 см. Ответ — на 8 см длиннее.
Дополнительные сведения
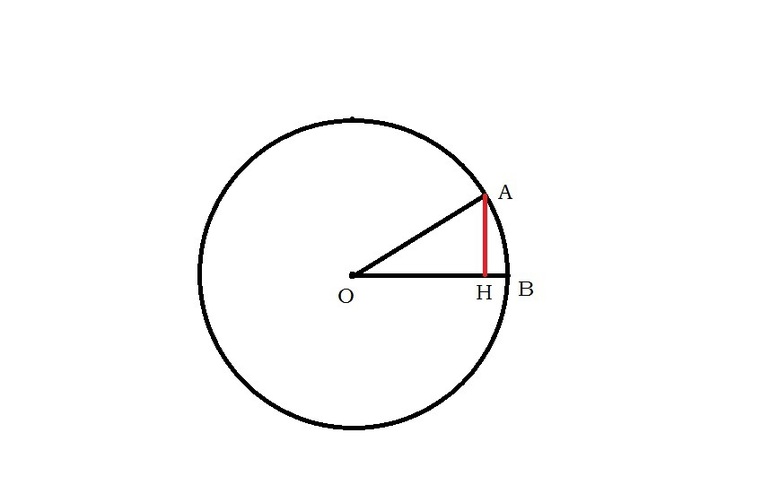
Если в окружности провести 2 радиуса, то в результате круг будет разделен на 2 части, которые называются секторами. Отрезки образуют центральный угол.
В чем разница между диаметра и радиуса?
Круг — плоская фигура, ограниченная окружностью, как апельсин и тарелка. Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
В чем разница между диаметром и радиусом?
Радиус — это отрезок прямой, который соединяет каждую точку окружности, которая находится на равном расстоянии от центра окружности, с центром окружности. Диаметр — это отрезок прямой линии, который соединяет любые две удаленные друг от друга точки окружности и всегда должен проходить через центр этой окружности.
В чем разница между радиусом и диаметром окружности?
Радиус: расстояние от центра окружности до его границы. Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам. Периметр (длина окружности): длина границы окружности.
Чем отличается диаметр от длины?
Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы). Также диаметром называют длину этого отрезка.
Что больше диаметр или окружность?
1. Длина окружности больше диаметра в 3,14 раза или в значение π.
Как провести диаметр окружности?
Если вам известна длина окружности, то, для того чтобы вычислить диаметр, разделите ее на π. Число π равно примерно 3,14; но чтобы получить наиболее точное значение, вам следует воспользоваться калькулятором. Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.
Как найти диаметр и радиус окружности?
R = D : 2, где D — диаметр. Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Как найти длину круга?
Формула Чтобы найти длину окружности, нужно либо диаметр окружности умножить на π≈3,1415926535…, либо найти удвоенное произведение радиуса и числа π. Здесь r — это радиус заданной окружности, а d — диаметр, π≈3,1415926535…. Радиусом окружности — отрезок, который соединяет центр окружности с точкой окружности.
Как называется хорда которая проходит через центр окружности?
Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы). Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. … Хорда, проходящая через центр окружности, является её диаметром.
Что касательная к окружности?
Касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания. … б) прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам. Пусть AB и AC — касательные к окружности с центром O.
Как пишется сокращенно диаметр?
Диаметр – это длинна отрезка прямой соединяющей поверхности окружности. Отрезок диаметра, в любом случае проходит только через центр окружности. Обозначают его обычно латинской буквой « D » или знаком « Ø ».
Чем отличается круг от окружности?
Окружность — это замкнутая кривая, все точки которой одинаково удалены от центра. Круг – это геометрическая фигура, которая ограничена окружностью. Радиус- это отрезок, соединяющий центр окружности с любой точкой на окружности.
Чему равен диаметр окружности если ее длина равна 1 31 4см?
Что такое диаметр и радиус окружности?
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Сколько радиусов может иметь окружность?
Вывод: в окружности можно построить сколько угодно радиусов. Все радиусы одной окружности равны.
Какой буквой обозначается окружность?
Окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности. Это расстояние называется радиус и в записях обозначается буквой R. Центр окружности чаще всего обозначают буквой O.
Определения понятий
Чтобы изобразить фигуру, достаточно обвести контур карандашом вокруг круглого предмета либо начертить при помощи циркуля. На месте прокола циркуля ставят точку, что и будет центром окружности.
Окружность — геометрическое место точек плоскости, в котором длина от точек к центру одинаковая. По-другому можно описать определение, что это замкнутая кривая, в которой править будут равные отрезки, проведенные от центра до краев фигуры. Круг — часть плоскости, которая ограничена окружностью.
Если поставить точку на окружности и соединить ее с центром, в результате получится отрезок. Таких отрезков можно нарисовать не один, сколько точек на окружности поставить — столько и будет таких отрезков, то есть бесчисленное количество.
Отрезок, который равен расстоянию от центра до границ окружности имеет название радиуса. Этот термин с латинскими корнями и в переводе означает луч либо спица колеса.
Первый раз о термине заговорили в 1569 году, и примерно через 100 лет он стал общепринятым. И не удивительно, так как в обиходе люди часто говорят, к примеру, «пожар в радиусе 10 км уничтожил все», «в радиусе 5 м нет видимости» и так далее.
Диаметром называется отрезок, который соединяет 2 точки окружности и проходит обязательно через центр круга. Такой отрезок делит круг на 2 части. По-другому — хорда, которая проходит через центр круга. Этот отрезок самый больший, который можно изобразить в круге, что и будет отличаться от других отрезков. Их можно изобразить в фигуре бесконечное число.
Обозначения и свойства
Понятия имеют принятые обозначения. Буквой d обозначают диаметр (в некоторых источниках обозначается перечеркнутой буквой о), а r — радиус. Для измерения используют:
Диаметр состоит из 2 радиусов, а это значит, если необходимо узнать, чему равен радиус, необходимо длину диаметра разделить напополам. То есть разница между ними в 2 раза. Не всегда два радиуса образуют диаметр: только при условии, если они находятся на одной прямой.
Для решений задач можно использовать формулу: d =2*r. Естественно, формула работает в обратном направлении, она будет выглядеть следующим образом: r = d/2.
Дано: r =80 мм, определить, на сколько сантиметров диаметр длиннее. Для решения задачи используют формулу d=2*r. Но для начала необходимо перевести миллиметры в сантиметры. 80 мм=8 см. Далее d=2*8=16 см. Чтобы вычислить отличие, необходимо 16−8=8 см. Ответ — на 8 см длиннее.
Дополнительные сведения
Если в окружности провести 2 радиуса, то в результате круг будет разделен на 2 части, которые называются секторами. Отрезки образуют центральный угол.