в чем различие медианы и биссектрисы треугольника
Треугольник. Важные факты о высоте, биссектрисе и медиане
Определения
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
Доказательство
Для других медиан треугольника \(ABC\) требуемое свойство доказывается аналогично.
Теорема
Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).
Доказательство
Теорема
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.
Доказательство
Теорема
Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:
Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
Доказательство
Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть \[\dfrac
Теорема
Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.
Доказательство
Треугольник
Рис. 1. Треугольник (общий случай)
Треугольник — замкнутая геометрическая фигура, состоящая из трёх отрезков (в общем случае, разных). В физике эти отрезки классически называются буквами латинского алфавита ( и т.д.), в отличие от обозначений в геометрии.
В случае, если у треугольника равны две стороны, данный треугольник называется равнобедренным.
В случае, если у треугольника все стороны одинаковы, он называется равносторонним.
В случае, если у треугольника один и углов прямой ( ), он называется прямоугольным.
Для произвольного треугольника вводят ряд отрезков, характеризующих треугольник и обладающих собственными свойствами:
Для разных типов треугольников поиск длин параметров треугольника может происходить по-разному. Для физических задач использование конкретной формулы диктуется конкретными данными задачи.
Рис. 2. Треугольник (биссектриса)
Биссектриса угла — геометрическое место точек, равноудалённых от сторон этого угла. Т.е. биссектриса — это линия, которая делит угол треугольника пополам (рис. 2). Известно, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
Для нахождения биссектрисы угла через различные данные можно пользоваться следующими соотношениями:
Медиана треугольника — отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Все медианы треугольника пересекаются в одной точке: данная точка делит медианы в соотношении 2 к 1, считая от вершины (рис. 3).
Рис. 3. Треугольник (медиана)
Для нахождения медианы треугольника через различные данные можно пользоваться следующими соотношениями:
Рис. 4. Треугольник (высота)
Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону или на её продолжение (рис. 4).
Для нахождения высоты треугольника через различные данные можно пользоваться следующими соотношениями:
Важно: то, какую формулу выбрать для решения конкретной задачи, зависит от того, что легче найти, исходя из дано.
Геометрия. 7 класс
Конспект урока
Медианы треугольника. Биссектрисы треугольника. Высоты треугольника
Перечень рассматриваемых вопросов:
Биссектриса угла – это луч, исходящий из вершины угла и делящий его на два равных угла.
Биссектриса угла треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Теоретический материал для самостоятельного изучения.
Вы уже знакомы с такими понятиями как треугольник, угол, биссектриса угла.
Разберем, как построить биссектрису треугольника, а также узнаем, что такое медиана и высота треугольника.
Начнём с понятия биссектриса угла треугольника. Это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. AF – биссектриса ∠A треугольника ABC.
В любом треугольнике биссектрисы пересекаются в одной точке.
Введём понятие медианы треугольника.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
BM – медиана треугольника ABC.
В любом треугольнике медианы пересекаются в одной точке.
Введём понятие высоты треугольника.
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
AH – высота треугольника ABC.
В любом треугольнике высоты или их продолжения пересекаются в одной точке.
Итак, сегодня мы узнали, какие отрезки называются медианой, биссектрисой, высотой треугольника, и научились их изображать с помощью чертёжных инструментов.
Рассмотрим, как можно решить задачу на доказательство, используя понятие «медиана треугольника».
На рисунке изображён треугольник ABC, при этом AD – медиана ∆ABC продолжена за сторону BC, так что AD = DE.
Докажем, что треугольники ABD и CED равны.
По условию в треугольниках ABD и CED: сторона AD равна стороне DE. Т. к. АD – медиана ∆ABC, то, по определению медианы, BD = DC.
∠ADB = ∠CDE (по свойству вертикальных углов).
Следовательно, ∆ABD = ∆CED (по первому признаку равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны).
Что и требовалось доказать.
Разбор решения заданий тренировочного модуля.
В треугольнике ABC проведены биссектрисы AD и BM, которые пересекаются в точке O. Найдите углы треугольника ABO, если ∠BAC = 50°, ∠ABC = 80°, а сумма углов треугольника ABO равна 180°.
1.Нарисуем рисунок по условию задачи.
2.По условию AD и BM – биссектрисы ∆ABC.
∠BAC = 50°, ∠BAC = 2∠BAO =50° → ∠BAO = 25°
∠ABC = 80°, ∠ABC= 2∠ABO = 80°→∠ABO = 40°
3.Т. к. сумма углов треугольника ABO равна 180°, то ∠ABO + ∠BAO + ∠AOB = 180°.
5.∠AOB = 180° – (25° + 40°) = 115°.
Ответ: ∠BAO = 25°, ∠ABO = 40°, ∠AOB = 115°.
В треугольнике COD: ∠O = 90°. Найдите ∠МОВ, если ОА – биссектриса угла ∠СОM, при этом ∠COА = 20°, а ВО– биссектриса ∠МОD.
1.По условию ∠СОD = 90°.
Кроме того, ОА – биссектриса угла ∠СОM → ∠МОА = ∠СОА = 20°.
2.ВО – биссектриса ∠МОD→∠ВОD = ∠МОВ.
3. ∠СОD = ∠МОА + ∠СОА + ∠ВОD + ∠МОВ = 20° + 20° + 2∠МОВ = 40° + 2∠МОВ = 90°.
Треугольник. Медиана, биссектриса, высота, средняя линия.
теория по математике 📈 планиметрия
Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
| Разносторонний | Равнобедренный | Равносторонний |
| Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС. | Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС. | Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС. |
 |  |  |
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.
По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.
По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.
По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.
Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
Теперь найдем CD=AC-AD=54-24=30
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
pазбирался: Даниил Романович | обсудить разбор | оценить
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0
pазбирался: Даниил Романович | обсудить разбор | оценить
Свойства медианы и биссектрисы треугольника планиметрия геометрия 10
Свойства медианы и биссектрисы треугольника
Свойства медианы и биссектрисы треугольника
Выполнил:
Ученик 10 «В» класса
Шраер Семен
Учитель: Дюпина Е.А.
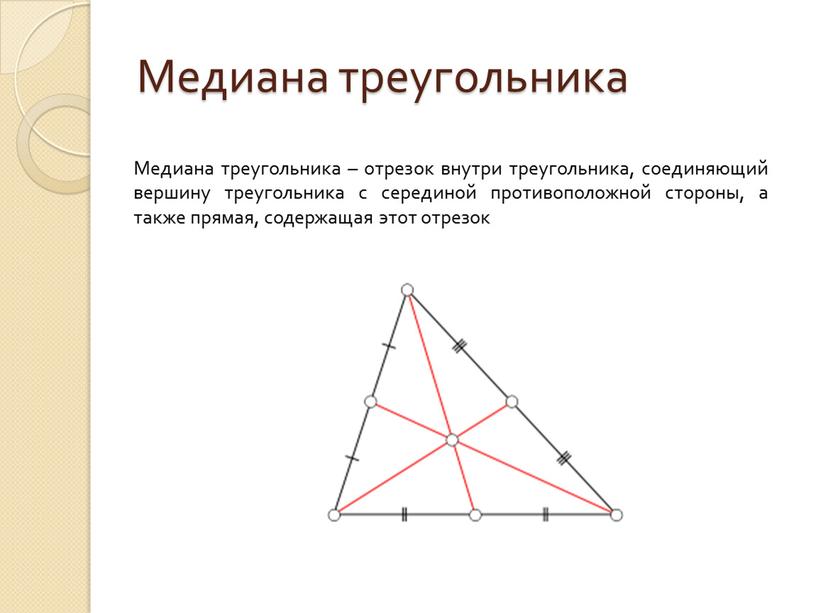
Медиана треугольника Медиана треугольника – отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок
Медиана треугольника – отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок
Свойства медианы треугольника 1
Свойства медианы треугольника
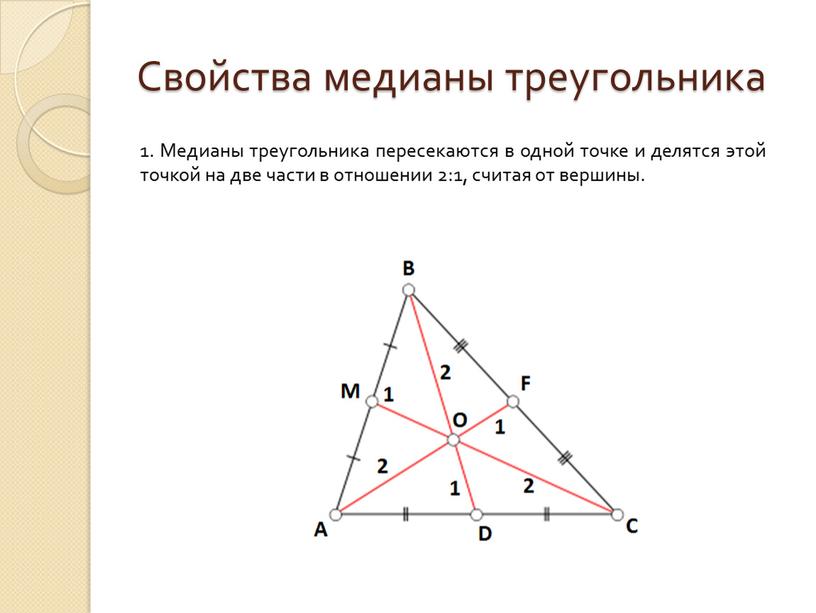
1. Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Свойства медианы треугольника 2
Свойства медианы треугольника
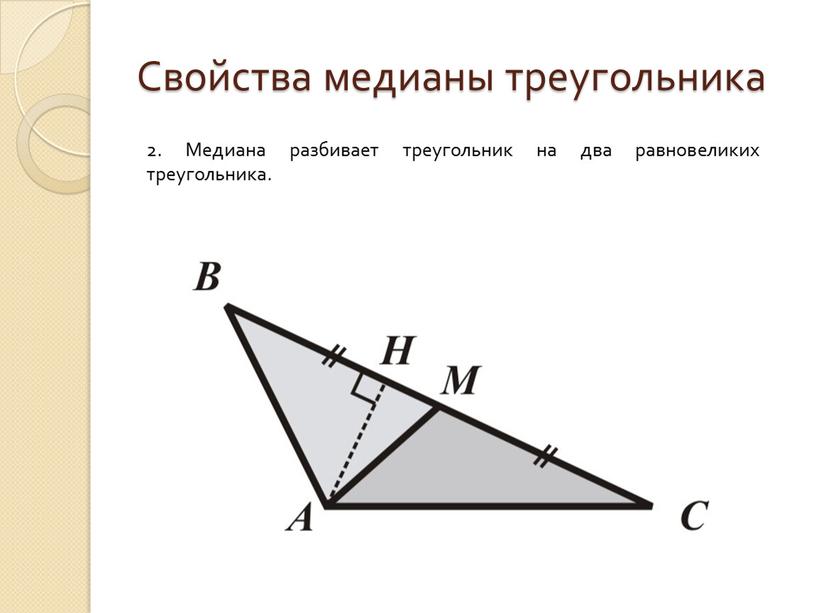
2. Медиана разбивает треугольник на два равновеликих треугольника.
Свойства медианы треугольника 3
Свойства медианы треугольника
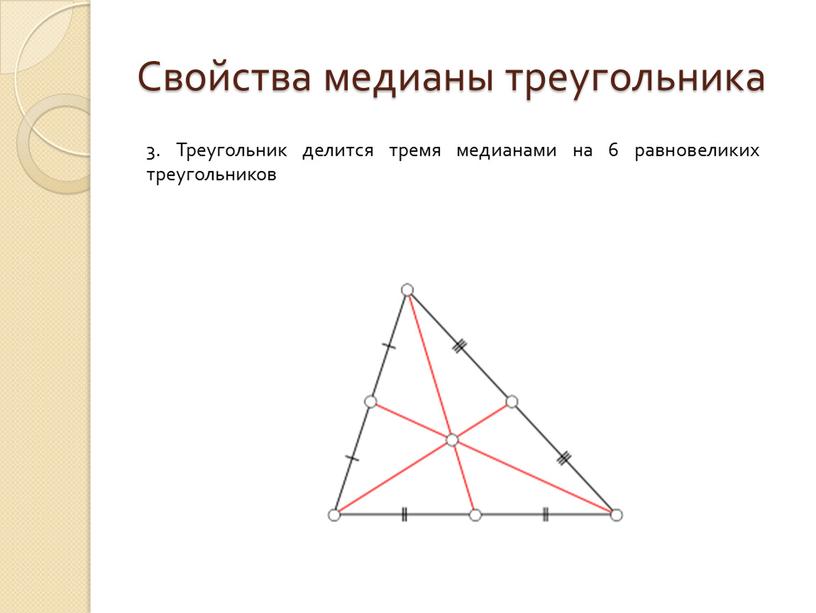
3. Треугольник делится тремя медианами на 6 равновеликих треугольников
Свойства медианы треугольника 4
Свойства медианы треугольника
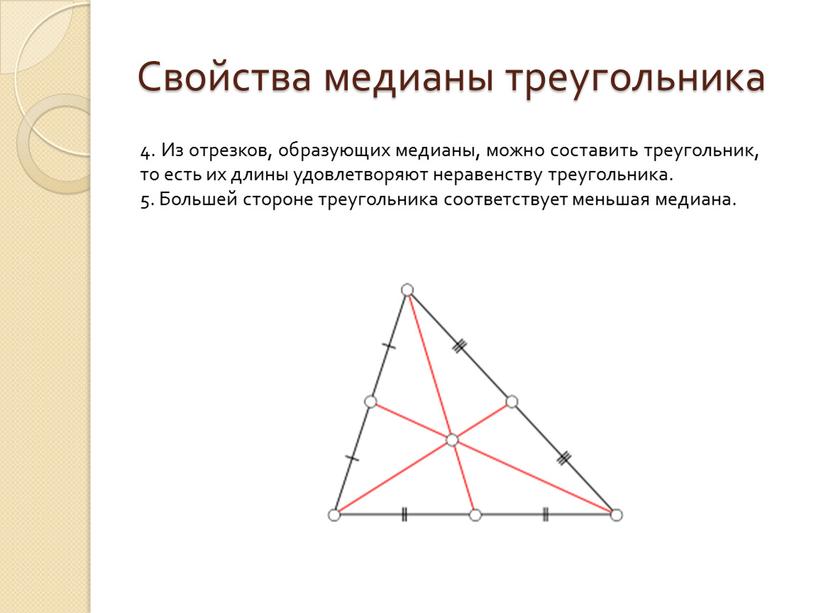
4. Из отрезков, образующих медианы, можно составить треугольник, то есть их длины удовлетворяют неравенству треугольника.
5. Большей стороне треугольника соответствует меньшая медиана.
Свойства медианы треугольника 6
Свойства медианы треугольника
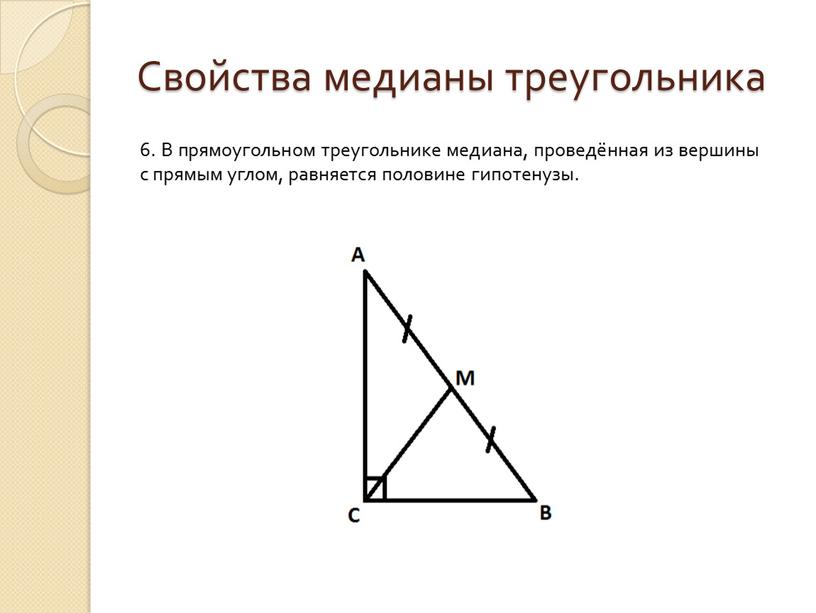
6. В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.