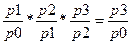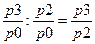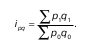в чем проявляется взаимосвязь цепных и базисных индивидуальных индексов
Цепные и базисные индексы
ИНДЕКСЫ
1.Общее понятие об индексах.
3.Общие (агрегатные) индексы.
4.Цепные и базисные индексы.
1. Общее понятие об индексах.
Индекс – это относительная величина, характеризующая изменение сложных общественных явлений во времени, пространстве или по сравнению с планом.
Индекс = величина сравнения (факт, отчет)
база сравнения (план, базис)
Выбор базы зависит от цели исследования. Если изучается динамика, то за базисную величину может быть взят размер показателя в периоде, предшествующем отчетному. Если необходимо осуществить территориальное сравнение, то за базу можно принять данные другой территории. За базу сравнения могут приниматься плановые показатели, если необходимо использовать индексы как показатели выполнения плана.
Статистика изучает в основном сложные экономические явления, которые состоят из элементов непосредственно несоизмеримых. Так, если электромеханический завод производит несколько видов продукции, то данные о выпуске продукции в натуральном выражении суммировать нельзя. Для того, чтобы показать общее изменение выпуска по нескольким видам продукции и вычисляются индексы. С их помощью можно дать обобщенную характеристику изменения себестоимости, цен, выпуска по нескольким видам продукции.
Индексы позволяют выявить степень изменения изучаемых социально-экономических явлений. С помощью индексов анализируется выполнение планов или нормативов, определяется влияние отдельных факторов на анализируемый показатель и др.
Индексы измеряются в коэффициентах или %-ах.
Индексы бывают индивидуальными и общими (агрегатными).
Для удобства применения индексного метода, составления формул индексов применяются условные обозначения:
i – индивидуальный индекс
I –общий (агрегатный) индекс
pi – цена за единицу продукции
qi – кол-во продукции одного вида в натуральном выражении
zi – себестоимость единицы продукции
Знак внизу справа означает период: 0 – базисный, 1 – отчетный.
2. Индивидуальные индексы.
Индивидуальные индексы –служат для характеристики изменения отдельных элементов сложного явления. Они характеризуют изменение индексируемой величины в текущм периоде по сравнению с базисным, т.е. во сколько раз она возросла или уменьшилась либо сколько % составляет ее рост или снижение. Можно выделить:
| Индивидуальный индекс физического объема | – это отношение количества товара одного вида, проданного в отчетном периоде, к количеству того же товара, проданного в базисном периоде. |
Поскольку базисный уровень индексируемого показателя приравнивается к 1 или 100%, то разность между полученным индексом и 1 или 100% характеризует относительную величину изменения количества проданного товара. По этому индексу можно определить и абсолютное изменение количества проданного товара в натуральном выражении как разность между числителем и знаменателем индекса.
| Индивидуальный индекс цен | – это отношение цены отдельного товара в отчетном периоде к цене его в базисном периоде. |
Разность между числителем и знаменателем его покажет абсолютное изменение цены за единицу товара в рублях.
| Индивидуальный индекс товарооборота (стоимости) | характеризует изменение товарооборота по одному товару и строится как отношение товарооборота отчетного периода к товарообороту базисного периода |
Разница между числителем и знаменателем его покажет абсолютное изменение товарооборота в рублях за счет двух факторов: изменения количества проданного товара и изменения цены этого товара.
Индивидуальные индексы взаимосвязаны между собой: индекс товарооборота равен произведению индекса физического объема на индекс цен, то есть
| Индивидуальный индекс себестоимости продукции | – это отношение себестоимости отдельного товара в отчетном периоде к его себестоимости в базисном периоде. |
Разница между числителем и знаменателем его покажет абсолютное изменение себестоимости единицы продукции в рублях.
3. Общие (агрегатные) индексы.
Общие индексы используются для сопоставления непосредственно несоизмеримых, разнородных явлений; они характеризуют изменение не отдельного элемента сложного явления, а всего явления в целом.
Например, с помощью общих индексов можно охарактеризовать динамику объемов всей выпускаемой продукции на мебельной фабрике, изготавливающей различные виды продукции: столы, стулья, диваны, шкафы. Однако нельзя просто сложить объемы продукции различных видов за два периода. Такое суммирование бессмысленно не только из-за различных единиц измерения (тонны, штуки, метры), но и из-за того, что каждый продукт имеет свое назначение и произведен с разными затратами средств и времени.
Чтобы сделать сопоставимыми несоизмеримые элементы, нужно выразить их общей мерой: стоимостью, трудовыми затратами и т.п. Эта задача решается построением и расчетом общих индексов.
Основной формой общих индексов являются агрегатные индексы.
Агрегатный индекс характеризует общее изменение объема производства, объема продаж, уровней цен и т.д. в целом по всей совокупности. Выделяют:
| Агрегатный индекс физического объема | — это отношение условной стоимости произведенных в текущем периоде товаров в ценах базисного периода к фактической стоимости товаров, произведенных в базисном периоде; |
| — характеризует, как изменился в среднем общий объем продукции. |

В основном при построении агрегатного индекса физического объема продукции в качестве соизмерителей применяются сопоставимые, неизменные, фиксированные цены на уровне базисного периода, что позволяет устранить влияние изменения цен на динамику количества продукции.
Абсолютное изменение физического объема:
| Агрегатный индекс цен | — изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде; |
| — характеризует, как изменились в среднем цены на различные виды продукции (фактическую экономию или перерасход). |
Абсолютное изменение цен:
| Агрегатный индекс стоимости продукции | — это отношение стоимости продукции текущего периода к стоимости базисного периода; |
| — характеризует изменение фактической стоимости произведенной или реализованной продукции. |
Абсолютное изменение стоимости в отчетном периоде по сравнению с базисным одновременно за счет изменения физического объема продаж и изменения цен:
Взаимосвязь индексов можно представить в виде:
4. Цепные и базисные индексы.
Если при исчислении индексов сравниваемых периодов три и более, то возникает вопрос о выборе базы сравнения. В зависимости от базы сравнения различают:
Выбор системы индексов определяется задачами анализа. Для оценки скорости происходящих изменений от периода к периоду используют цепные индексы. Если же необходимо определить общие изменения экономического явления за конкретный исторический период, рассчитывают базисные индексы.
Цепные и базисные индексы могут быть как индивидуальные, так и общие.
Базисные индивидуальные индексы физического объема:



Цепные индивидуальные индексы физического объема:



Базисный агрегатный индекс физического объема продукции:


Цепной агрегатный индекс физического объема продукции:


Цепные и базисные индексы



Для более глубокого изучения динамики экономических процессов, выявления закономерностей и тенденций их развития недостаточно рассчитать индекс только за отчетный год, для этого проводятся сопоставления индексов за ряд последовательных периодов. В этом случае следует различать цепные и базисные индексы.
Цепные индексы – это система индексов в ряду динамики, рассчитанных последовательно как отношение текущего уровня ряда к предыдущему уровню ряда. Индексируемая величина каждый раз меняется и представляет собой каждый следующий период. Базисная величина также меняется и представляет собой величину, непосредственно стоящую перед индексируемой величиной.
Базисные индексы – это система индексов в ряду динамики, рассчитанных последовательно как отношение каждого последующего уровня к одной и той же базисной величине. В качестве базисной величины обычно применяется начальный уровень динамического ряда.
Цепные индексы применяются для оценки скорости изменения изучаемого явления от периода к периоду. Базисные же индексы применяются для оценки степени изменения явления за большой промежуток времени, включающий в себя несколько отчетных периодов.
Система цепных и базисных индексов может быть исчислена как для отдельного элемента сложной совокупности – это индивидуальные индексы, так и для всей совокупности – это общие индексы.
Рассчитать цепные и базисные индивидуальные индексы, характеризующие изменение остатков готовой продукции организации на складе.
Таблица 34 – Запасы готовой продукции вида «А» на складе
по состоянию на начало кварталов
| Квартал | Отчетный год | 1 квартал следующего года | |
| 1 кв. | 2 кв. | 3 кв. | 4 кв. |
| Объем запаса на начало квартала, ед. |
1) Рассчитаем цепные индексы динамики:
– 2-ой кв. по отношению к 1-му: 545 / 540 = 1,009 или 100,9%
– 3-ий кв. по отношению ко 2-му: 552 / 545 = 1,013 или 101,3%
– 4-ый кв. по отношению к 3-му: 562 / 552 = 1,018 или 101,8%
– 1-ый кв. сл. года к 4-му кв.: 580 / 562 = 1,032 или 103,2 %
Изучая уровни ряда, мы уже можем отметить негативную тенденцию изменения запасов готовой продукции – они возрастают от квартала к кварталу. Кроме того, цепные индексы показали возрастающую скорость увеличения запасов готовой продукции. Если во втором квартале запас возрос только на 0,9 %, то в первом квартале следующего года – уже на 3,2 %. Это подтверждает негативную тенденцию сокращения рынка сбыта данной продукции.
2) Рассчитаем базисные индексы динамики по отношению к первому кварталу:
– 2-ой кв.: 545 / 540 = 1,009 или 100,9 %
– 3-ий кв.: 552 / 540 = 1,022 или 102,2 %
– 4-ый кв.: 562 / 540 = 1,041 или 104,1 %
– 1-ый кв. сл. года: 580 / 540 = 107,4 %
Базисные индексы также показывают возрастающую скорость увеличения запасов. Если по сравнению с первым кварталом запас возрос во втором квартале только на 0,9 %, то в первом квартале следующего года – уже на 7,4 %. В течение всего года объем запаса накапливался и за весь год возрос на 7,4 %.
Цепные и базисные индивидуальные индексы имеют следующую взаимосвязь:
– последовательное произведение цепных индексов n-периода и всех предыдущих периодов дает базисный индекс n- периода в анализируемом ряду:
– отношение базисного индекса n-периода к предыдущему индексу n-1 периода дает цепной индекс n-периода:
в 3-ем квартале: 1,022 / 1,009 = 1,013 или 101,3 %
в 4-ом квартале: 1,041 / 1,022 = 1,018 или 101,8 %
в 1-ом квартале сл. года: 1,074 / 1,041 =1,032 или 103,2 %.
Аналогичные правила приемлемы и для агрегатных индексов с постоянными весами. Приведем несколько последовательных формул расчета цепных агрегатных индексов физического объема продукции:
Формулы расчета базисных агрегатных индексов физического объема продукции:
Произведение цепных агрегатных индексов дает базисный индекс:
Отношение двух соседних базисных агрегатных индексов дает цепной агрегатный индекс, например:
Базисные и цепные индексы, их взаимосвязь



Для изучения динамики показателя за ряд последовательных периодов рассчитывается система цепных и базисных индексов.
Базисные индексы характеризуют относительное изменение уровня изучаемого явления в какой-то определенный период по сравнению с периодом, принятым за базу сравнения.
Цепные индексы характеризуют относительное изменение уровня изучаемого явления по сравнению с предшествующим периодом. Система цепных и базисных индексов может быть исчислена как для отдельного элемента сложного явления (индивидуальные индексы), так и для всего сложного явления (общие индексы).
Для индивидуальных индексов цен, физического объема справедливо следующее правило:
1. Произведение цепных индексов за определенный период дает базисный индекс за этот же период.




2. Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода.
Ip=
40. Индивидуальные базисные и цепные индексы. Общие индексы
40. Индивидуальные базисные и цепные индексы. Общие индексы
Для определения статистических индексов нужно иметь данные за два периода или два сравниваемых уровня.
Если существуют данные за определенный ряд периодов или уровней, то в качестве базы для сравнения можно принять один и тот же начальный уровень или уровень предыдущего периода. В первом случае получим индексы с постоянной базой – базисные, а во втором – индексы с переменной базой – цепные.
В экономическом анализе базисные и цепные индексы обладают определенными значениями.
Базисные экономические индексы характеризуют изменение статистических процессов за длительный период времени по отношению к одной отправной точке, но если возникнет необходимость следить за текущими изменениями статистического процесса, то применяются цепные индексы.
Если на основе базисных и цепных индексов исследуется один и тот же период, то это обозначает, что между ними есть взаимосвязь – это произведение цепных индексов, равное базисному. Такая взаимосвязь принесет возможность вычислить базисные индексы по данным цепных индексов, и наоборот.
Общие индексы характеризуют соотношение совокупности статистических процессов или явлений, состоящей из разнородных, непосредственно несоизмеримых элементов. Для определения общей стоимости различных видов продукции в качестве соизмерителя используется обычно цена за единицу продукции, для определения общей себестоимости или производственных затрат – себестоимость единицы продукции, общих затрат труда – затраты труда на производство единицы продукции и т. д.
Общее изменение товарооборота от стоимости проданных товаров можно определять, сопоставив общую стоимость проданных товаров в отчетном периоде по ценам отчетного периода с общей стоимостью проданных товаров в базисном периоде по ценам базисного периода.
Формула общего индекса товарооборота:
Аналогично индексу товарооборота рассчитываются индексы продукции, потребления и т. д.
Приведенная выше формула индекса товарооборота называется агрегатной (от лат. aggrega – «присоединяю»). Агрегатными называются индексы, числители и знаменатели которых представляют собой суммы, произведения или суммы произведений уровней изучаемого статистического явления. Агрегатная формула индекса – основная и наиболее распространенная формула экономических индексов. Агрегатная формула индекса показывает относительное изменение исследуемого экономического процесса и абсолютные размеры этого изменения.
Расчет агрегатного индекса цен был предложен немецким экономистом Г. Пааше.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
Индексы российского рынка
Индексы российского рынка Шансы того, сохранится или нет тенденция движения акции, равны пятьдесят на пятьдесят. Адам Смит. Биржа – игра на деньги Важность расчета индекса трудно переоценить, однако для его повсеместного признания важную роль играет то, кем
Фондовые индексы
Фондовые индексы Фондовый индекс – это средняя величина курсов акций по определенной группе компаний по отношению к базовой величине.Фондовый индекс позволяет отслеживать общее направление движения рынка. Кроме того, индексное инвестирование (вложение денег в акции
Рынок и индексы
Рынок и индексы Итак, что такое рынок ценных бумаг? Это место, где торгуют ценными бумагами, или, иначе, фондовая биржа (stock exchange). Долгое время фондовые биржи были физическими местами, где собирались вместе торговцы ценными бумагами – брокеры. Физически эти места есть и
40. Средние индексы
40. Средние индексы В зависимости от методологии расчета индивиду–альных и сводных индексов различают средние ариф–метические и средние гармонические индексы. Други–ми словами, общий индекс, построенный на базе индивидуального индекса, принимает форму среднего
49. Биржевые индексы
49. Биржевые индексы Биржевые индексы – это ключевые показатели, используемые для оценки, исследования и прогнозирования общего положения в фондовой торговле и в отдельных отраслях.Исчисление биржевых индексов можно производить по разной методике.Одни индексы
4. Индексы и уровни цен
4. Индексы и уровни цен Для начала определим, что ВВП может иметь две формы: номинальную и реальную. Номинальный ВВП соответственно рассчитывается посредством учета текущего уровня цен, а реальный – в базисных ценах, что позволяет оценить изменения в объеме
3. Рыночная власть фирмы, ее индексы
3. Рыночная власть фирмы, ее индексы Фирмы-производители поставляют на рынок товаров и услуг различные блага для удовлетворения потребностей общественных масс. Соответственно они осуществляют свою деятельность под воздействием величины и структуры потребительского
2. Агрегатные индексы качественных показателей
2. Агрегатные индексы качественных показателей Каждый качественный показатель связан с тем или иным объемным показателем, в расчете на единицу измерения которого он исчисляется (или к единице измерения которого относится). Так, цена единицы товара связана с его
3. Агрегатные индексы объемных показателей
3. Агрегатные индексы объемных показателей Объемные показатели могут быть соизмеримыми (объем продукции или товаров одного вида) и несоизмеримыми (объем продукции или товаров разного вида – Q). Соизмеримые объемные показатели могут непосредственно суммироваться, и
6. Средние индексы
6. Средние индексы В зависимости от методологии расчета индивидуальных и сводных индексов различают средние арифметические и средние гармонические индексы. Другими словами, общий индекс, построенный на базе индивидуального индекса, принимает форму среднего
Вопрос 61 Биржевые индексы
Вопрос 61 Биржевые индексы Ответ Биржевые индексы представляют собой агрегированные показатели движения биржевых курсов акций.Индекс ММВБ является взвешенным по эффективной капитализации показателем рынка наиболее ликвидных акций российских эмитентов, допущенных к
39. Понятие об индексах. Индивидуальные индексы
39. Понятие об индексах. Индивидуальные индексы Индекс (Index) означает указатель, показатель.В статистике индекс – это относительная величина, характеризующая изменения во времени и в пространстве уровня изучаемого общественного явления (процесса), или степень выполнения
ЛЕКЦИЯ № 11. Индексы
ЛЕКЦИЯ № 11. Индексы 1. Понятие об индексах Особым видом относительных величин являются индексы. Индекс (Index) означает указатель, показатель. Особенности индексов в том, что:1) с помощью индексов одним числом можно выразить соотношение разнородных явлений, показатели
2. Индивидуальные индексы
2. Индивидуальные индексы Индивидуальные индексы характеризуют соотношение отдельных элементов совокупности.Примером индивидуальных индексов может быть процент выполнения плана или динамика выпуска одного вида продукции, процент выполнения плана или динамика
4. Другие агрегатные индексы
4. Другие агрегатные индексы Рассмотрим некоторые из агрегатных индексов.1. Индекс себестоимости продукции показывает, во сколько раз себестоимость в отчетном периоде в среднем выше или ниже базисной или плановой себестоимости, а также абсолютный размер экономии или