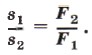в чем проигрывают пользуясь рычагом дающим выигрыш в силе

Простые механизмы.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.

Рычаг.

Рис. 1. Рычаг

Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.

Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).

Неподвижный блок.

Важной разновидностью рычага является блок — укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.

На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).

Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.

Подвижный блок.

Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).

Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.

Наклонная плоскость.

Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.

Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:

Проектируем на ось :

Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.

Широко применяемыми разновидностями наклонной плоскости являются клин и винт.

Золотое правило механики.

Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.

т. е. той же величине, что и без использования рычага.

т. е. ту же самую, что и при вертикальном поднятии груза.

Данные факты служат проявлениями так называемого золотого правила механики.

Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.

Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.

КПД механизма.

На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн,
которая совершается для тех же целей в реальной ситуации.

Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.

Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.

Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:

КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.

Ускорения нет, поэтому силы, действующие на груз, уравновешены:

Проектируем на ось X:

Проектируем на ось Y:

Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:

Источник

§ 62. Равенство работ при использовании простых механизмов. «Золотое правило» механики

Рассмотренные нами простые механизмы применяют при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу.

Естественно, возникает вопрос: позволяя получить выигрыш в силе или в пути, нельзя ли с помощью простых механизмов получить выигрыш и в работе? Для ответа на поставленный вопрос проделаем опыт.

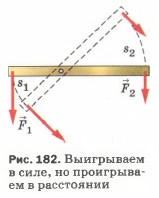
Уравновесив на рычаге две какие-нибудь разные по модулю силы F₁ и F₂ (рис. 182), приводят рычаг в движение. При этом оказывается, что за одно и то же время точка приложения меньшей силы F₂ проходит больший путь s₂, а точка приложения большей силы F₁ — меньший путь s₁. Измерив эти пути и модули сил, находят, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам:

Таким образом, действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути.

Произведение силы F на путь s есть работа. Наши опыты показывают, что работы, совершаемые силами, приложенными к рычагу, равны друг другу:

Итак, при использовании рычага выигрыша в работе не получают.

Пользуясь рычагом, мы можем выиграть или в силе, или в расстоянии. Если мы силу приложим к длинному плечу, то выиграем в силе, но во столько же раз проиграем в расстоянии. Действуя же силой на короткое плечо рычага, мы выиграем в расстоянии, но во столько же раз проиграем в силе.

Существует легенда, что Архимед, восхищённый открытием правила рычага, воскликнул: «Дайте мне точку опоры, и я подниму Землю!»

Конечно, Архимед не мог бы справиться с такой задачей, если бы даже ему и дали точку опоры (которая должна была бы находиться вне Земли) и рычаг нужной длины.

Не даёт выигрыша в работе и неподвижный блок, в чём легко убедиться на опыте (см. рис. 168). Пути, проходимые точками приложения сил F₁ и F₂, одинаковы, одинаковы и силы, а значит, одинаковы и работы.

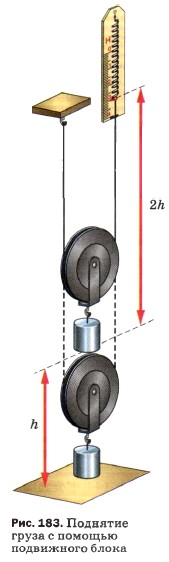
Можно измерить и сравнить между собой работы, совершаемые с помощью подвижного блока. Чтобы при помощи подвижного блока поднять груз на высоту h, необходимо конец верёвки, к которому прикреплён динамометр, как показывает опыт (рис. 183), переместить на высоту 2h.

Таким образом, получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути, следовательно, и подвижный блок не даёт выигрыша в работе.

Многовековая практика показала, что ни один из механизмов не даёт выигрыша в работе. Применяют же различные механизмы для того, чтобы в зависимости от условий работы выиграть в силе или в пути.

Уже древним учёным было известно правило, применимое ко всем механизмам: во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии. Это правило назвали «золотым правилом» механики.

Вопросы

1. Какое соотношение существует между силами, действующими на рычаг, и плечами этих сил (см. рис. 167)?
2. Какое соотношение существует между путями, пройденными точками приложения сил на рычаге, и этими силами?
3. В чём проигрывают, пользуясь рычагом, дающим выигрыш в силе?
4. Во сколько раз проигрывают в пути, используя для поднятия грузов подвижный блок?
5. В чём состоит «золотое правило» механики?

Упражнение 33

1. С помощью подвижного блока груз подняли на высоту 1,5 м. На какую длину при этом был вытянут свободный конец верёвки?

2. Рабочий с помощью подвижного блока поднял груз на высоту 7 м, прилагая к свободному концу верёвки силу 160 Н. Какую работу он совершил? (Вес блока и силу трения не учитывать.)

3. Как применить блок для выигрыша в расстоянии?

4. Как можно соединить друг с другом неподвижные и подвижные блоки, чтобы получить выигрыш в силе в 4 раза; в 6 раз?

5. Решите задачу 2, учитывая вес блока, равный 20 Н.

Источник