в чем преимущества выборочного наблюдения перед сплошным
Выборочное наблюдение и Виды совокупности
Выборочное наблюдение
Выборочное наблюдение есть такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, затем отобранная часть изучается, а далее результаты распространяются на всю исходную совокупность. В задачах по статистике наблюдение происходит таким образом, что эта часть отобранных единиц в уменьшенном масштабе представляет всю совокупность.
Виды совокупности
Генеральная совокупность — это совокупность, из которой производится отбор. Все обобщающие показатели данной совокупности называются генеральными.
Выборочная совокупность — это совокупность отобранных единиц. Все ее обобщающие показатели получили название выборочных.
Преимущества выборочного метода над сплошным
Главные причины, по которым во многих случаях выборочному наблюдению отдают предпочтение перед сплошным:
Основные этапы проведения выборочного наблюдения
Виды выборки по методу
Повторная выборка имеет место в схеме возвратного шара. Она характеризуется тем, что численность единиц генеральной совокупности в процессе выборки остается постоянной. Определенную единицу, попавшую в выборку, после регистрации опять возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц снова попасть в выборку. Данный вид выборки очень редко можно встретить в социально-экономической жизни. Вероятность попадания любой единицы в выборку равна 1/N, и она остается постоянной на протяжении всей процедуры отбора.
Доля выборки
Доля выборки рассчитывается как отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности и определяется по формуле:
где N — объем генеральной совокупности (число входящих в нее единиц);
n — объем выборки (число обследованных единиц).
Выборочная доля
Выборочная доля (или частность) рассчитывается как отношение числа единиц, которые обладают изучаемым признаком m, к общему числу единиц выборочной совокупности n и определяется по формуле:
ЛЕКЦИЯ №6. Выборочное наблюдение
ЛЕКЦИЯ №6. Выборочное наблюдение
1. Общее понятие о выборочном наблюдении
Статистическое наблюдение можно организовать как сплошное и несплошное. Сплошное предусматривает обследование всех единиц изучаемой совокупности явления, несплошное – лишь ее части. К несплошному относится и выборочное наблюдение.
Выборочное наблюдение является одним из наиболее широко применяемых видов несплошного наблюдения. В основе этого наблюдения лежит идея о том, что отобранная в случайном порядке некоторая часть единиц может представлять всю изучаемую совокупность явления по интересующим исследователя признакам. Целью выборочного наблюдения является получение информации прежде всего для определения сводных обобщающих характеристик всей изучаемой совокупности. По своей цели выборочное наблюдение совпадает с одной из задач сплошного наблюдения, и поэтому речь может идти о том, какое из двух видов наблюдения – сплошное или выборочное – целесообразнее провести.
При решении этого вопроса необходимо исходить из следующих основных требований, предъявляемых к статистическому наблюдению:
1) информация должна быть достоверной, т. е. максимально соответствовать реальной действительности;
2) сведения должны быть достаточно полными для решения задач исследования;
3) отбор информации должен быть проведен в максимально сжатые сроки для обеспечения ее использования в оперативных целях;
4) денежные и трудовые затраты на организацию и проведение должны быть минимальными.
При выборочном наблюдении эти требования обеспечиваются в большей мере, чем при сплошном. Преимущества выборочного наблюдения по сравнению со сплошным в полной мере можно оценить, если оно организовано и проведено в строгом соответствии с научными принципами теории выборочного метода. Таким принципом является обеспечение случайности отбора единиц и достаточного их числа. Соблюдение принципа позволяет получить такую совокупность единиц, которая по интересующим исследователя признакам представляет всю изучаемую совокупность, т. е. является репрезентативной (представительной).
При проведении выборочного наблюдения обследуются не все единицы изучаемого объекта, т. е. не все единицы генеральной совокупности, а лишь ее некоторая часть, специальным образом отобранная. Первый принцип отбора – обеспечение случайности – заключается в том, что при отборе каждой из единиц изучаемой совокупности обеспечивается равная возможность попасть в выборку. Случайный отбор – это не беспорядочный отбор. Случайный отбор можно обеспечить только при соблюдении определенной методики (например, осуществляя отбор по жребию, применяя таблицы случайных чисел и т. д.).
Второй принцип отбора – обеспечение достаточного числа отобранных единиц – тесно связан с понятием репрезентативности выборки. Понятие репрезентативности отобранной совокупности единиц не следует понимать как ее представительность во всех отношениях, т. е. по всем признакам изучаемой совокупности. Такое представительство обеспечить практически невозможно. Любое выборочное наблюдение проводится с определенной целью и четко сформулированными конкретными задачами, и понятие репрезентативности должно быть связано с целью и задачами исследования. Отобранная из всей изучаемой совокупности часть должна быть репрезентативной прежде всего в отношении тех признаков, которые изучаются или оказывают существенное влияние на формирование сводных обобщающих характеристик.
Введем некоторые понятия, используемые в выборочном наблюдении. Генеральной совокупностью называется вся изучаемая совокупность единиц, подлежащая изучению по интересующим исследователя признакам. Выборочной совокупностью называется отобранная в случайном порядке из генеральной совокупности некоторая ее часть. К данной выборке предъявляется требование репрезентативности, что означает возможность, изучая лишь часть генеральной совокупности, распространять полученные выводы на всю совокупность. Характеристиками генеральной и выборочной совокупностей могут служить средние значения изучаемых признаков, их дисперсии и средние квадратические отклонения, мода и медиана и др.
Исследователя могут интересовать и распределения единиц по изучаемым признакам в генеральной и выборочной совокупностях. В этом случае частоты называются соответственно генеральными и выборочными.
Система правил отбора и способов характеристики единиц изучаемой совокупности составляет содержание выборочного метода. Суть выборочного метода состоит в получении первичных данных, осуществляемых наблюдением выборки с последующим обобщением, анализом и их распространением на всю генеральную совокупность с целью получения достоверной информации об исследуемом явлении.
Репрезентативность выборки обеспечивается соблюдением принципа случайности отбора объектов совокупности в выборку. Если совокупность является качественно однородной, то принцип случайности реализуется простым случайным отбором объектов выборки. Простым случайным отбором называют такую процедуру образования выборки, которая обеспечивает одинаковую вероятность для каждой единицы совокупности быть выбранной для наблюдения, для любой выборки заданного объема.
Итак, цель выборочного метода – сделать вывод о значении признаков генеральной совокупности на основе информации от случайной выборки из этой совокупности.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
Наблюдение за моделями
Наблюдение за моделями Когда люди – или рынки – кажутся вам иррациональными, весьма вероятно, что вы просто не в состоянии понять их язык. Сны, лепет маленьких детей, произведения искусства – очень часто проникновенная истина преподносится способами, наделенными скорее
69. Первичное наблюдение
69. Первичное наблюдение Первичное наблюдение – основа функционирования хозяйственного учета. Оно охватывает:• оценку и критерии отбора фактов хозяйственной жизни;• однозначное объявление объектов и событий, отражаемых в учете;• совмещение во времени оформления
Наблюдение за конкурентами
Наблюдение за конкурентами Итак, мы выяснили, что примерно три четверти менеджеров регулярно собирают информацию о своих конкурентах (в первую очередь, ценовую). Это наблюдение за действиями конкурентов может стимулировать имитацию чужих, более успешных стратегий или,
ЛЕКЦИЯ № 2. Статистическое наблюдение
ЛЕКЦИЯ № 2. Статистическое наблюдение 1. Понятие о статистическом наблюдении, этапы его проведения Глубокое всестороннее исследование любого экономического или социального процесса предполагает измерение его количественной стороны и характеристику его качественной
ЛЕКЦИЯ №6. Выборочное наблюдение
ЛЕКЦИЯ №6. Выборочное наблюдение 1. Общее понятие о выборочном наблюдении Статистическое наблюдение можно организовать как сплошное и несплошное. Сплошное предусматривает обследование всех единиц изучаемой совокупности явления, несплошное – лишь ее части. К
Наблюдение за состоянием рынка
Наблюдение за состоянием рынка Каждая из вышеуказанных стратегий работает лучше всего в свое время – когда цены движутся определенным образом или сам рынок находится в определенном состоянии. Как показано на рисунке 2–1, спекулятивные рынки могут быть в одном из
ЛЕКЦИЯ № 2. Статистическое наблюдение
ЛЕКЦИЯ № 2. Статистическое наблюдение 1. Организация статистического наблюдения Статистическое наблюдение – это организованная работа по сбору первичных сведений об изучаемых массовых явлениях и процессах общественной жизни. Статистическое наблюдение проводится
Наблюдение
Наблюдение Третий способ учиться на примере других людей – это умение наблюдать. Наблюдайте что делают люди, добившиеся успеха. Почему? Потому что успех оставляет ключи к разгадке. Понаблюдайте, как преуспевающий человек пожимает кому-то руку. Понаблюдайте, как
Наблюдение 1. Продавать нужно так же, как вы покупаете
Наблюдение 1. Продавать нужно так же, как вы покупаете Загляните в свою папку со спамом в электронной почте. Да, вы. Да, сейчас.Я подожду…Так-так. Вы вернулись. Отлично.Вы видели предложение от компании, занимающейся заправкой картриджей? А презентацию по поисковой
Наблюдение
Наблюдение Наблюдать – означает изучать работников за работой, подмечая, что они делают, как они это делают и сколько времени на это уходит. Этот метод больше всего подходит для рутинной административной роли или роли, связанной с физическим трудом, но он редко
Наблюдение
Наблюдение Самые пытливые учатся с помощью наблюдения. Вы можете понаблюдать за теми, чья работа вам нравится, и попробовать сделать так же, как они. Вы можете поэкспериментировать с новой моделью поведения, наблюдая за реакцией окружающих. Если вы предпочитаете молчать,
Простейший метод – личное наблюдение
Простейший метод – личное наблюдение Один из основных способов сбора информации, а также один из самых простых – персональное наблюдение. Отслеживая события или поведение людей из других компаний, лично делая покупки, вы получаете возможность осознать факторы,
Выборочное тестирование
Выборочное тестирование Когда я обсуждал эту историю с коллегами, Екатерина Мальчук предложила свой вариант решения:«По поводу обсуждаемого случая с магазином светильников мне хочется предложить несколько другой вариант. Суть в общем-то, та же, в повышении цены на
За монитором: виртуальное наблюдение
За монитором: виртуальное наблюдение За исключением редких технологий, которыми могут пользоваться разве что правительственные организации, проследить за поведением онлайн-покупателей нереально. Однако у интернет-магазинов есть огромное количество данных помимо
5. СОВЕТ: Тайное наблюдение
5. СОВЕТ: Тайное наблюдение На чем бы ни базировалась информация – на поведении или на чем-то еще, – важно уточнить, знают ли потребители, что изучается в исследовании. Если им известен его предмет, то вероятность, что этот факт повлияет на их реакцию, невероятно
2. Наблюдение за экспертом
2. Наблюдение за экспертом Вспоминается недавний разговор с одной нашей клиенткой, обучающей сотрудников международной компании стоимостью несколько миллиардов долларов. Мы попросили ее поделиться впечатлениями об онлайн-обучении и вспомнить, трудно ли было его
Выборочное наблюдение. Его преимущества и недостатки
Выборочное наблюдение– метод получения данных, при котором информация собирается не со всех элементов объекта исследования (генеральной совокупности), а только с его относительно малой части. Что это дает? Какие здесь плюсы и минусы? Для ответов на эти и другие вопросы создана отдельная рубрика о выборочном наблюдении и проверке статистических гипотез. Данная статья является вводной, где читатель в основных чертах познакомится с выборочным наблюдением, его преимуществами и недостатками.
Главная причина – это доступность, что выражается в относительно небольших затратах на проведение (по сравнению со сплошным наблюдением). Нет необходимости задействовать большое количество людей. На свод и обработку данных также не требуется много времени (опять же относительно сплошного наблюдения). Такой расклад делает выборочное наблюдение весьма привлекательным методом для многих исследователей (социологов, маркетологов, экономистов, контролеров качества, ньюсмейкеров и т.д и т.п.).
Второй причиной широкого использования выборок я бы назвал тот факт, что выборка часто являться единственным способом сбора данных, т.к. сплошное наблюдение в некоторых ситуациях вообще недоступно. Например, невозможно проверить эффективность лекарства на всех пациентах, которые будут его принимать в будущем. Невозможно также подсчитать количество животных или растений в лесу путем их тотального пересчета или количество проросших семян на поле в несколько гектар. Поэтому к выборочному методу прибегают еще и вынуждено, а не только из-за экономии. Есть и другие причины, но это были основные. Я считаю.
Теперь обозначим главные недостатки выборочного метода. Недостаток, по сути один. Он заключается в том, что показатели, рассчитанные по выборке, всегда ошибочны. Вот так, немного и немало – они всегда неверны относительно истинного (неявного) показателя из генеральной совокупности данных. Чтобы мы не рассчитали по выборке, это всегда неправда, точнее сказать – не совсем правда. Если показатель, рассчитанный по генеральной совокупности, отражает истинное состояние дел (при точных замерах, разумеется), то выборка всегда дает погрешность. Такова цена за все те возможности, которые она дает.
Почему же выборка дает ошибку? Потому что структура данных выборки всегда хоть немного, но отличается от структуры генеральной совокупности. Отсюда все значения показателей, рассчитанных по выборке, будут хоть немного, но отличаться от аналогичных показателей, рассчитанных по генеральной совокупности. В этом легко убедиться, если несколько раз подбросить монетку и подсчитать количество выпавших орлов и решек. Маловероятно, что их соотношение будет 50/50. Хотя в генеральной совокупности (бесконечно большого количества подбрасываний) соотношение именно 50/50.
Почему тогда используют выборку, если она всегда дает ошибочные результаты? Да потому что лучше иметь неточные данные, чем не иметь вообще никаких. При этом правильное проведение выборочного наблюдения может дать довольно таки приемлемые по точности результаты. Допустим, мы не знаем истинное соотношение выпадения орлов и решек (настоящей вероятности). Но, сделав 100 подбрасываний и получив, к примеру, соотношение 55/45 у нас уже будет неплохой ориентир. То есть 55/45 гораздо ближе к 50/50, чем, скажем, 10/90, если сделать такое предположение наугад. Далее эти результаты можно уточнить или сделать определенные допуски на разброс. Для анализа выборочных данных разработана специальная технология, которая выдвигает ряд требований и правил для того, чтобы результаты были насколько это возможно точными и трактовались насколько возможно корректно.
Самое первое требование относится к исходным данным. Они должны быть репрезентативными, то есть содержать в себе всю информацию о качестве генеральной совокупности. Внутренняя структура выборки должна соответствовать структуре данных в генеральной совокупности. Образно выражаясь, выборка должна быть максимально точной уменьшенной копией оригинального объекта исследования. Имея в наличии такую уменьшенную модель, можно проводить различные опыты и результаты распространять на оригинал. Как, например, перед строительством корабля вначале делают уменьшенную копию и проверяют в специальном бассейне с волнами и штормами. Если модель при испытаниях не переворачивается, тогда есть надежда, что и корабль не потонет.
Теория вероятностей утверждает, что для сохранения исходной структуры данных отбор следует производить в случайном порядке из всей генеральной совокупности. Ключевое слово – в случайном порядке. Это значит, что любой элемент может быть отобран с одинаковой вероятностью.
Далее по выборочным данным рассчитывают различные показатели, которые на самом деле называются оценками. Исследователь пытаетсяоценить значение показателя по выборочным данным и получает что-то близкое к истинному значению, но всегда с некоторым отклонением (что-то вроде соотношения 55/45 вместо реального 50/50 при подбрасывании монеты). Совпадение может произойти исключительно по чистой случайности. Это первое важное понятие, которое нужно зазубрить на всю жизнь. Оценка показателя – это всего лишь оценка и при повторном проведении эксперимента (выборки) обязательно будет другой.
И быть беде, если бы ошибка выборки была абсолютно непредсказуема и не имела пределов. Результаты выборочных измерений были бы равносильны методу «пальцем в небо». К всеобщему счастью это не так. Оценки, рассчитанные по репрезентативной выборке, обладают рядом полезных свойств, которые с той или иной вероятностью определяют границы их возможных изменений, то есть интервал, в пределах которого находится истинный показатель по генеральной совокупности. Хорошее понимание таких свойств позволяет исследователю делать достаточно правдивые заключения обо всей генеральной совокупности. Естественно, делая поправку на погрешность.
Оценка показателя не всегда рассчитывается по той же формуле, что и сам показатель. Например, средняя арифметическая, будучи оценкой математического ожидания, имеет по сути ту же формулу – сумма произведений отдельных значений на их вероятности (частоты). Это хорошо видно по формуле средней арифметической взвешенной, если все слагаемые в числителе разделить на знаменатель (сумму весов). А вот формула дисперсии по выборке немного отличается от формулы дисперсии по генеральной совокупности. Если этот момент проигнорировать, то дисперсия по малой выборке получится слегка заниженной. В общем формулы показателей и их оценок лучше не путать. Хотя при выборке размером более 50 наблюдений, разница практически исчезает.
Индекс объема
2) для бесповторной выборки:
где N – количество единиц всей генеральной совокупности. Из приведенных формул видно, что бесповторная выборка обеспечивает более точные результаты, чем повторная, поскольку множитель (1-n/N) всегда меньше единицы, то есть он уменьшает величину ошибки бесповторной выборки. Поэтому на практике используют преимущественно бесповторную выборку. Величина предельной ошибки выборки зависит от таких факторов: вариации признака в генеральной
обратно пропорциональна. Поэтому, чтобы уменьшить ошибку выборки, например, в 2 раза, объем выборки должен возрасти в 4 раза..
Понятие выборочного наблюдения и его преимущества
Статистическая методология исследования массовых явлений различает, как известно, два способа наблюдения в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное.
Под выборочным наблюдениемпонимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные в определенном порядке.
Цель выборочного наблюдения состоит в том, чтобы по характеристикам отобранной части единиц судить о характеристиках всей совокупности.
Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами средств и труда.
В проведение ряда исследований выборочный метод является единственно возможным, например, при контроле качества продукции, если проверка сопровождается уничтожением или разложением исследуемых образцов (определение качества продукта, установление носкости обуви, прочности ткани на разрыв).
При соблюдении правил научной организации выборочный метод дает достаточно точные результаты, поэтому его целесообразно применять для проверки данных сплошного учета.
Для того чтобы по выборке можно делать вывод она должно быть репрезентативной (представительной), т.е. полно и адекватно представлять свойства генеральной совокупности. Репрезентативность выборки может быть обеспеченна только при объективности отбора данных.
При контроле качества товаров в экономических исследованиях эксперимент может проводиться на основе малой выборки.
Под малой выборкой понимается несплошное статистическое обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Объем малой выборки обычно не превышает 30 единиц и может доходить до 4 — 5 единиц.
Отбор единиц в выборочную совокупность может быть повторным и бесповторным.
При повторной выборке общая численность единиц генеральной совокупности в процессе выборки остается неизменной. Ту или иную единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц вновь попасть в выборку («отбор по схеме возвращенного шара»). Например, при исследовании магазина один и тот же покупатель может совершить дважды покупку. Повторная выборка в социально-экономической жизни встречается редко. Обычно выборку организуют по схеме бесповторной выборки.
При бесповторной выборке единица совокупности, попавшая выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует; т.е. последующую выборку делают из генеральной совокупности уже без отобранных ранее единиц («отбор по схеме невозвращенного шара»). Таким образом, при бесповторной выборке численность единиц генеральной совокупности сокращается в процессе исследования. Но получаемые при этом результаты являются более точными, чем при повторной выборке.
Основные характеристики параметров генеральной и выборочной совокупностей обозначаются символами:
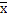
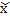
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Сплошное и выборочное наблюдение: теоретический аспект
Рубрика: 14. Экономика и организация предприятия, управление предприятием
Дата публикации: 01.11.2016
Статья просмотрена: 8712 раз
Библиографическое описание:
Григорьева, Н. В. Сплошное и выборочное наблюдение: теоретический аспект / Н. В. Григорьева. — Текст : непосредственный // Проблемы и перспективы экономики и управления : материалы V Междунар. науч. конф. (г. Санкт-Петербург, декабрь 2016 г.). — Санкт-Петербург : Свое издательство, 2016. — С. 107-110. — URL: https://moluch.ru/conf/econ/archive/219/10945/ (дата обращения: 05.12.2021).
В данной работе рассмотрены два вида выборочного наблюдения: сплошное и выборочное. Выделены основные положительные стороны каждого метода. Рассмотрена одна из форм сплошного наблюдения и виды выборочного наблюдения. Кратко рассмотрены применение каждого метода в конкретных случаях.
Ключевые слова: статистическое наблюдение, сплошное наблюдение, единовременный учет, выборочное наблюдение, ошибки регистрации
Успех дела сбора качественных и полных данных об исследуемой совокупности, прежде всего, зависит от выбора вида статистического наблюдения. Сама статистика имеет многовековую историю. Она возникла на основе общественных потребностей: подсчет населения, учет земельных угодий, учет имущества. В статистической практике применяются два вида статистического наблюдения. К ним относится сплошное и выборочное наблюдение. В зависимости от поставленных задач выбирают тот или иной вид наблюдения.
По обхвату объема единиц обследуемой совокупности различают сплошное и несплошное наблюдение.
Сплошное наблюдение ̶ это такой вид наблюдения, в ходе которого обследованию подвергаются все единицы изучаемой совокупности [2, 125 с.]. Сплошное наблюдение является генеральной совокупностью. К примерам сплошного наблюдения можно отнести: перепись населения за определенный период и перепись мелкой промышленности. Текущая статистика, которая базируется на отчетности, относится к сплошному наблюдению. Это может быть из-за того, что она, текущая статистика, в целях контроля выполнения государственного плана охватывает все без исключения предприятия и организации.
К форме сплошного наблюдения можно отнести единовременные учёты. Единовременный учет ̶ это организованное наблюдение, которое проводится единовременно или же периодически [2, 129 с.]. Данный учёт характеризует массовое явление на определенный момент времени. Применяется он для получения детальных сведений, уточнения данных, которые были получены на основе других источников. Так, например, во время Великой Отечественной Войны в СССР производили единовременный учет служащих и рабочих промышленных предприятий. А все полученные данные были использованы для рационального распределения и использование кадров.
При проведении сплошного наблюдения могут возникнуть ошибки регистрации. Ошибки регистрации ̶ это несоответствие между установленными наблюдениями и фактическими значениями изучаемых величин [2, 131 с.].
В настоящее время различают два вида шибок: [3]
Контроль материалов сплошного наблюдения осуществляется с точки зрения полноты охвата объекта и с точки зрения качества. Основная цель сплошного наблюдения ̶ это формирование официальной статистической информации, которая содержит комплексную и детализированную характеристику экономической деятельности хозяйств субъектов. Сплошное наблюдение нужно для того, чтобы улучшить качество социально-экономического прогнозирования, а также выработке мер по повышению эффективности функционирование российской экономики.
Предпосылкой для возникновения сплошного наблюдения является определение подлежащих регистрации признаков.
На сегодняшний день статистическая практика применения сплошного наблюдения ограничена в связи с ее недостатками.
Основные недостатки сплошного наблюдения в статистических исследованиях:
Факторы, от которых зависит процент не обследуемых единиц:
Также для некоторой совокупности данного наблюдения оказывается невозможным. Например, когда обследование приводит к порче изучаемой единицы ̶ исследование качества продукции.
Если мы не можем изучить единицу совокупности с помощью сплошного наблюдения, то мы прибегаем к выборочному наблюдению. В ходе которого обследуются части единиц. Выборочное наблюдение – это вид несплошного наблюдения, при котором характеристика всей совокупности (генеральной) дается по некоторой ее части (по выборке), отобранной в случайном порядке [1, 98 с.]. Выборочное наблюдение имеет несколько положить сторон в отличие от сплошного наблюдения. Например, представленное наблюдение является наиболее совершенным. Кроме этого выборочное наблюдение является обоснованным научным способом. Теоретическая основа выборочного метода –это теория вероятностей и закон больших чисел [1, 101 с.]. Ей посвящены работы П. Л. Чебышева, А. М. Ляпунова, П. Лапласа, А. А. Макарова. В этих работах доказывается, что при случайном отборе единиц совокупности среднее значение изучаемого признака в этой совокупности стремиться к характеристикам генеральной совокупности. Иными словами, по величине среднего значения признака в выборочной совокупности можно судить о среднем значении данного признака в генеральной совокупности.
Таким образом, появилась возможность судить о всей генеральной совокупности на основе изучения выборки. Это доказывается тем, что генеральная и выборочная средняя различаются на величину ошибки выборки. Следовательно, задача метода состоит в изучении и измерении случайных ошибок репрезентативности.
Показатели генеральной и выборочной совокупности:
− Генеральная совокупность(N) – это совокупность единиц социально-экономического явлении, которые обладают изучаемым признаком;
− Генеральная доля(p) – наблюдение альтернативных признаков;
− Выборочная совокупность (n) – число отобранных для наблюдения единиц генеральной совокупности;
− Выборочная доля (Ѡ) – наблюдение альтернативных признаков.
Рассматриваемое выборочное наблюдение проходит по определенной схеме. Рассмотрим данную схему:
На сегодняшний день существует несколько способов случайного отбора. Они могут различаться схемой отбора единиц из генеральной совокупности, а так же видом указанного метода. В каждом конкретном случае выбор того или иного способа зависит от сущности изучаемого явления, объема совокупности, вариации ее признаков, финансовых возможностей исследователей.
Выделяют две схемы отбора. Первая – это повторный отбор, а второй –это бесповторный отбор. Виды выборочного метода наблюдения различаются по способу организации. К ним относят: собственно случайный, механический, типический и серийный.
Дадим небольшую характеристику каждому виду выборочного наблюдения.
Серийно-случайный отбор. Представляет собой отбор единиц из генеральной совокупности. Отбор проходит случайно при условии вероятности выбора любой единицы из генеральной совокупности. Этот отбор проводится путем жеребьевки, отбора на основе таблиц случайных чисел и другие. Случайно-серийный отбор может быть как повторный, так и бесповторный.
Механический отбор. Данный отбор предполагает, упорядоченно расположенные единицы совокупности отбирают по одной через определенный интервал. Этот интервал называется — интервал выборки. Этот отбор осуществляется только бесповторным способом. При данном отборе отобранные единицы не имеют вероятностного характера. Случайные ошибки обусловлены наличием случайности в расположении к материалу изучаемой совокупности.
Типичный (районированный) отбор. Представленный отбор имеет свою определенную организацию. На первой стадии генеральная совокупность разбивается на однородные группы. А уже на второй стадии из каждой выделенной группы в случайном порядке или же механически отбираются отдельные единицы. Выбирается, как правило, в объеме, пропорциональном численности единиц по группам в генеральной совокупности.
Серийная (гнездовая) выборка. Данная выборка обеспечивает наименьшую репрезентативность. Является наименее трудоемким способом организации отбора. В серийной выборке выбираются целые серии. Внутри отобранной серии обследуют все единицы совокупности. Данный отбор удобен в том случае, когда единицы совокупности объединены в небольшие группы.
Задачи, которые возникают при применении выборочного наблюдения: [4, 81 с.]
− для точности результатов, с заданной вероятностью, определяют объема выборки;
− определение возможного предела ошибки репрезентативности, гарантированного с заданной вероятностью, и сравнение его с величиной допустимой погрешности;
− определение вероятности того, что ошибка выборки не превысит допустимой погрешности.
Если сравнивать сплошное и выборочное наблюдение, то можно заметить, что выборочное наблюдение имеет больше преимуществ перед сплошным наблюдением. Кратко рассмотрим основные преимущества выборочного наблюдения.
Преимущества выборочного наблюдения: [4, 93 с.]
− это конечно же экономия затрат труда и средств;
− уничтожения обследуемых единиц.
Таким образом, на основе всего сказанного, можно сделать вывод, о том, что в статистическом наблюдении выделяю выборочное и сплошное наблюдение. В зависимости от целей и поставленных задач, выбирают тот или иной вид наблюдения. Каждый вид наблюдения имеет свою определенную характеристику и изучает различные статистические единицы. С помощью сплошного наблюдения можно изучить, например, перепись населения, а с помощью выборочного наблюдения можно изучить, качество продукции.
Ключевые слова
Похожие статьи
Участие студентов в спортивной жизни университета на примере.
Генеральной совокупностью статистического наблюдения (N) являлись студенты второго курса, а выборочная совокупность (n) заранее не планировалась (студентам было предложено пройти опрос по желанию).
Исследование предпочтений студентов к виду транспорта
В данной статье рассмотрены результаты выборочного наблюдения на тему «Исследование предпочтений студентов к виду транспорта».
Ключевые слова: статистическое исследование, выборка, анкетирование, респонденты, вид транспорта.
Вариационный ряд антропометрических признаков студенток.
Математическая статистика — наука, которая изучает вопросы соотношения генеральной совокупности и выборок.
В том случае, если в выборке число наблюдений менее 60, значения признака не группируют в классы.
Методы математической статистики в технических исследованиях
Одним из основных понятий является выборочная совокупность – понятие, лежащее в основе всех статистических методов, и представляющее собой часть объектов из генеральной совокупности, отобранных для изучения.
Статистическая обработка результатов гидравлического.
Сплошное и выборочное наблюдение: теоретический аспект.
Представляет собой отбор единиц из генеральной совокупности. Этот интервал называется — интервал выборки.
Проблемы применения статистических критериев проверки.
Ключевые слова:выборка, генеральная совокупность
Рассмотрим выборочный вектор х=(x1. xn) из генеральной совокупности, характеризуемой случайной величиной Х=(X1,…,Xn).
можно представить в виде: где d — наибольший общий делитель n и m.
Сочетание и комбинирование методов сбора информации.
При осуществлении метода наблюдения (и в первую очередь включенного) параллельно проводится специально организованный опрос.
В итоге исследователи получают данные из разных источников и в разном виде. Это вынуждает специалистов уделять особое внимание.
К задаче распознавания образов без учителя в технической.
Выборочное наблюдение – это вид несплошного наблюдения, при котором характеристика всей совокупности (генеральной) дается по некоторой ее части (по выборке), отобранной в случайном порядке [1, 98 с.