в чем особенность диаграммы растяжения хрупкого материала

Диаграммы растяжения для пластичных и хрупких материалов

Диаграммы растяжения для пластичных и хрупких материалов

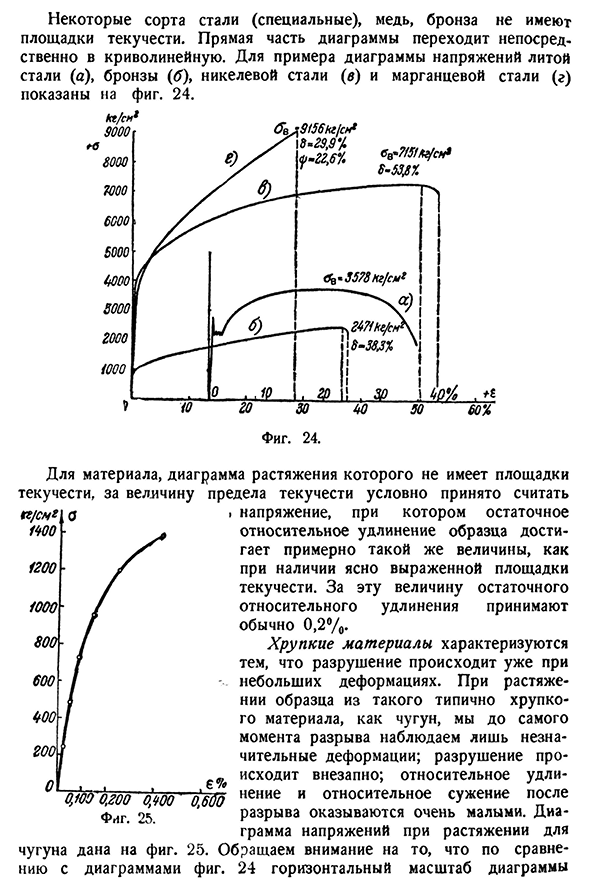
как показано на рисунке. 21.56 экспериментальное исследование[гл.] Некоторые марки стали (специальные), меди, бронзы не имеют предела текучести.

Прямая часть диаграммы переходит непосредственно в криволинейную часть. Например, диаграмма Людмила Фирмаль

напряжений литой стали (a), бронзы (tf), никелевой стали (b) и марганцевой стали (d) показана на рисунке. 24. Если диаграмма растяжения представляет собой материал, который не имеет предела текучести, предел текучести считается обычным К / см * около 140ОБУТ > Тысяча. Шесть сотен.- Шесть сотен. Четыреста. Две сотни. Одна тысяча двести Отчет 0>У0 0,200 0,400 ″ 0,600 Фигура. Двадцать

пять Напряжение, когда остаточное удлинение образца достигает приблизительно той же величины, что и при наличии четко определенной точки текучести. Для этого значение остаточного удлинения обычно составляет 0,2%. Хрупкий материал характеризуется тем, что разрушение происходит уже при небольших деформациях. При растяжении образца обычно хрупкого материала,

пластмассы. Зависимость деформации от растягивающего напряжения хрупкого материала обычно недостаточна по закону крюка, и на рисунке вместо прямой части при малых напряжениях образуется слегка изогнутая линия. Таким образом, модуль упругости, равный касательной (§ 12) угла наклона относительно оси поперечной оси в контакте с диаграммой напряжений, фактически не может рассматриваться как постоянная величина такого материала. Из-за этих напряжений непосредственный модуль упругости из-за криволинейной выпуклости будет отличаться. Но

в пределах этих напряжений Между силой упругости е, Или Людмила Фирмаль

напряжение тока и co- Материал обычно функционирует в структурах, но отклонения от наблюдаемого закона крюка незначительны. Итак, в реальном расчете мы заменяем криволинейную часть рисунка соответствующим кодом(рис. 26) и постоянное рассмотрение модуля Е. Это связано с тем, что механические свойства хрупкого материала позволяют варьировать по отдельным образцам в более широком диапазоне, чем свойства пластического материала, можно определить взаимосвязь между напряжением и деформацией.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Виды диаграмм растяжения

Виды диаграмм растяжения

Различные материалы по-разному ведут себя под нагрузкой, характер деформаций и разрушения зависит от типа материалов.

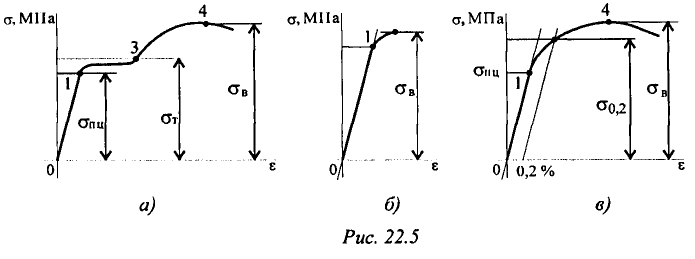
Принято делить материалы по типу их диаграмм растяжения на три группы. К первой группе относят пластичные материалы, эти материалы имеют на диаграмме растяжения площадку текучести (диаграммы первого типа) (рис. 22.5а). Ко второй группе относятся хрупкие материалы, эти материалы мало деформируются, разрушаются по хрупкому типу. На диаграмме нет площадки текучести (рис. 22.56).

К третьей группе относят материалы, не имеющие площадку текучести, но значительно деформирующиеся под нагрузкой, их называют пластично-хрупкими (рис. 22.5в).

Таким образом, хрупкий и пластично-хрупкий материалы не имеют площадки текучести, а в справочниках отсутствует характеристика «предел текучести». По этой особенности их можно узнать.

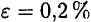
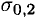
Пластично-хрупкие материалы значительно деформируются, этого нельзя допустить в работающей конструкции. Поэтому их деформацию обычно ограничивают. Максимально возможная относительная деформация . По величине максимально возможной деформации определяется соответствующее нормальное напряжение , которое принимают за предельное.

Эта теория взята со страницы решения задач по предмету «техническая механика»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Диаграммы растяжения для пластичных и хрупких материалов

Лекция 6

В предыдущих параграфах рассмотрена физическая картина явлений при растяжении образцов из пластичного материала типа малоуглеродистой стали. Для других видов материалов, дающих при растяжении пластическую деформацию, получаются диаграммы напряжений примерно того же вида, что и на рис.16.Некоторые сорта стали (специальные), медь, бронза не имеют площадки текучести. Прямая часть диаграммы переходит непосредственно в криволинейную. Для примера диаграммы напряжений литой стали (а), бронзы (б), никелевой стали (в) и марганцовистой стали (г) показаны на рис. 20.

Для материала, диаграмма растяжения которого не имеет площадки текучести, за величину предела текучести условно принято считать напряжение, при котором остаточное относительное удлинение образца достигает примерно такой же величины, как при наличии ясно выраженной площадки текучести. За эту величину остаточного относительного удлинения принимают обычно 0,2%.

Хрупкие материалы характеризуются тем, что разрушение происходит уже при небольших деформациях. При растяжении образца из такого типично хрупкого материала, как чугун, мы до самого момента разрыва наблюдаем лишь незначительные деформации; разрушение происходит внезапно; относительное удлинение и относительное сужение после разрыва оказываются очень малыми. Диаграмма напряжений при растяжении для чугуна дана на рис.21. Обращаем внимание на то, что по сравнению с диаграммами рис.20 горизонтальный масштаб диаграммы рис.21 увеличен примерно в 40 раз, а вертикальный — примерно в 6 раз.

Как правило, хрупкие материалы плохо сопротивляются растяжению; их предел прочности на разрыв оказывается малым по сравнению с пределом прочности пластичных материалов.

Зависимость деформаций от напряжений при растяжении хрупких материалов обычно плохо изображается законом Гука; на диаграмме вместо прямолинейного участка мы уже при низких напряжениях получаем слегка искривленную линию, т. е. не наблюдается строго линейной пропорциональности между силой или напряжением и соответствующей деформацией.

Таким образом, модуль упругости Е, равный (§ 11) тангенсу угла наклона относительно оси абсцисс касательной к диаграмме напря­жений, собственно говоря, нельзя считать для таких материалов постоянной величиной; он меняется в зависимости от величины того напряжения, для которого мы вычисляем деформацию. Чем эти напряжения больше, тем модуль меньше или больше, в зависимости оттого, куда направлена выпуклость кривой диаграммы — вверх или вниз.

Однако в пределах тех напряжений, при которых материал обычно работает в сооружениях, наблюдающиеся отклонения от закона Гука незначительны. Поэтому при практических расчетах заменяют криволинейную часть диаграммы соответствующей хордой (рис. 22) и считают модуль Е постоянным. Это тем более допустимо, что механические характеристики хрупких материалов изменяются для отдельных образцов в более широких пределах, чем характеристики пластичных материалов; поэтому нет смысла пользоваться более точными выражениями зависимости между напряжениями и деформациями

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Диаграмма растяжения хрупкого материала

Пластичность – способность материала без разрушения получать большие остаточные деформации.

Хрупкость – способность материала разрушаться при очень малых остаточных деформациях.

Две основные характеристики пластичности:

1) относительное удлинение образца при разрыве,

2) относительное сужение поперечного сечения образца при разрыве.

Относительное удлинение образца при разрыве – отношение абсолютного удлинения образца при разрыве к его первоначальной длине (рис. 14):

где 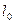– длина расчетной части образца до начала нагружения (первоначальная длина); – суммарная длина обоих участков расчетной части образца после разрыва.

Рис. 14. Определение относительного удлинения образца при разрыве

Величину можно определить по формуле для вычисления , предварительно определив по диаграмме. Экспериментально находят, сложив обе части разорванного образца по месту разрыва и измерив штангенциркулем длину между нанесёнными до проведения испытаний рисками.

Рис. 15. Определение суммарной длины обоих участков расчетной части образца после разрыва и диаметра шейки в месте разрыва

Условно принято, что если то материал пластичный (малоуглеродистая сталь, алюминий, латунь), а если то хрупкий (чугун, высокоуглеродистая инструментальная сталь).

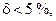
Относительное сужение поперечного сечения образца при разрыве – отношение абсолютного уменьшения площади поперечного сечения образца при разрыве к его первоначальной площади:

где – первоначальная площадь поперечного сечения образца ( – начальный диаметр расчетной части образца);

– конечная площадь поперечного сечения шейки образца после разрыва ( –диаметр шейки образца в месте разрыва).

Диаграмма растяжения хрупкого материала (чугун, высокоуглеродистая сталь) не имеет площадки текучести и зоны упрочнения (рис. 16). Шейка на образце из хрупкого материала не образуется. Поэтому основная механическая характеристика хрупкого материала – предел прочности .

Рис. 16. Диаграмма растяжения хрупкого материала

Контрольные вопросы

1. Дайте определение центрального растяжения (сжатия) стержня.

2. Сформулируйте правило знаков при центральном растяжении (сжатии).

3. Что такое абсолютная продольная деформация стержня?

4. Что такое относительная продольная деформация стержня?

5. Дайте определение относительной поперечной деформации стержня.

6. Напишите формулу, выражающую зависимость между относительной поперечной и относительной продольной деформацией.

7. Что называют коэффициентом Пуассона?

8. В каких пределах изменяется коэффициент Пуассона для изотропных материалов? В каких пределах находятся его значения для большинства металлов и сплавов?

9. Сформулируйте закон Гука. Границы применимости закона Гука.

10. В каких пределах изменяется модуль Юнга для сталей?

11. По какой формуле определяются нормальные напряжения при растяжении (сжатии)?

12. По какой формуле определяется абсолютное удлинение однородного стержня при постоянной нормальной силе и постоянной площади сечения?

13. При каких условиях проводятся испытания на растяжение?

14. Как выглядят образцы для испытаний на растяжение?

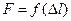
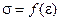
15. С какой целью диаграмму растяжения вида перестраивают в диаграмму ?

16. Нарисуйте диаграмму растяжения малоуглеродистой стали. Назовите все участки диаграммы растяжения малоуглеродистой стали.

17. Какие относительные продольные деформации называют упругими, а какие – пластическими?

18. Что такое предел пропорциональности?

19. Что такое предел упругости?

20. Что такое предел текучести?

21. Для каких материалов наблюдается отсутствие площадки текучести? Как выглядит при этом диаграмма растяжения?

22. Что такое условный предел текучести? Когда используют это понятие?

23. Чем объясняется появление на образце линий Чернова – Людерса?

24. В чём состоит суть процесса образования пластических деформаций?

25. Что такое предел прочности?

26. Образец был нагружен до точки К, лежащей на площадке текучести диаграммы растяжения малоуглеродистой стали, а затем разгружен. Покажите, как пройдет линия разгрузки? Покажите на этой диаграмме упругие и пластические относительные продольные деформации?

27. Образец был нагружен до точки К, лежащей в зоне упрочнения диаграммы растяжения малоуглеродистой стали, а затем разгружен. Покажите, как пройдет линия разгрузки? Покажите на этой диаграмме упругие и пластические относительные продольные деформации?

28. Чем диаграмма растяжения малоуглеродистой стали отличается от диаграммы сжатия малоуглеродистой стали? Как происходит сжатие пластичного образца, растяжение пластичного образца?

29. Чем отличаются диаграммы растяжения пластичного и хрупкого материалов и почему?

30. Чем отличаются диаграммы сжатия пластичного и хрупкого материалов и почему?

31. Чем отличаются диаграммы растяжения и сжатия хрупкого образца?

32. Образец был нагружен до точки К, лежащей в зоне упрочнения диаграммы растяжения малоуглеродистой стали, затем разгружен, а потом снова нагружен. Как видоизменится диаграмма растяжения при повторном нагружении образца?

33. В чем заключается явление наклёпа?

34. Объясните явление наклепа с помощью диаграммы растяжения малоуглеродистой стали.

35. Дайте определения понятиям «пластичность», «хрупкость».

36. Какие показатели пластичности вы знаете? Напишите формулы для их вычисления.

Порядок проведения работы

1. Замерить штангенциркулем начальные размеры рабочей части образца: диаметр и длину, подсчитать начальную площадь поперечного сечения .

2. Поместить образец в захваты испытательной машины.

3. Включить машину. Плавно увеличивая нагрузку, довести образец до разрушения.

4. Снять диаграмму растяжения с диаграммного аппарата.

5. Подсчитать с учётом масштаба значения усилий:

F_пц – продольная сила при пределе пропорциональности;

F_т – продольная сила при пределе текучести;

F_max – продольная сила при пределе прочности;

F_р – продольная сила при разрыве образца.

Разделив значения этих усилий на – первоначальную площадь образца, определить значения σ_пц, σт, σ_B, σ_р.

6. Подсчитать с учётом масштаба значения абсолютных деформаций:

∆l_пц – продольная сила при пределе пропорциональности;

∆l _т – продольная сила при пределе текучести;

∆l _в – продольная сила при пределе прочности;

∆l _р – продольная сила при разрыве образца.

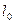
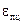
Разделив значения этих абсолютных деформаций на – начальную расчетную длину образца, определить соответствующие относительные продольные деформации , , , .

7. Определить модуль Юнга, разделив σ_пцна .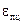

8. Выбрав произвольную точку К в зоне упрочнения диаграммы растяжения и предположив, что нагрузка образца проводится до этой точки, построить линию разгрузки. Определить 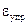–упругую деформацию, – остаточную (пластическую) деформацию, – полную относительную продольную деформацию.

9. Из точки D, соответствующей разрыву образца, провести прямую DL, параллельную начальному участку ОА, до пересечения с осью абсцисс. Измерив отрезок ОL, определить – относительное удлинение образца при разрыве.

10. Вынуть части разорванного образца из захватов испытательной машины. Сложить обе части разорванного образца по месту разрыва и измерить – суммарную длину обоих участков расчетной части образца после разрыва и – диаметр шейки в месте разрыва. Найти относительное сужение поперечного сечения образца при разрыве .

СПИСОК ЛИТЕРАТУРЫ

Буланов Э.А., Тарасов А.С., Зубарев А.А. Лабораторный практикум по курсу «Прикладная механика». Раздел «Сопротивление материалов». – М.: МГТУ им. А.Н. Косыгина, 2001. – 31 с.

Епифанов А.П., Морозов А.Н. Виртуальные лабораторные работы по сопротивлению материалов и прикладной механике. – Красноярск: КФ ИрГУПС, 2005. – 34 с.

Ицкович Г.М. Сопротивление материалов: Учеб. для техникумов. – 4-е изд., перераб. и доп. – М.: Высш. шк., 1970. – 488 с.

Карцов С.К. Журнал лабораторных работ по курсу «Сопротивление материалов». – М.: МАДИ (ГТУ), 2007. – 17 с.

Морозов А.Н. Лабораторный практикум по сопротивлению материалов и прикладной механике. – Красноярск: КФ ИрГУПС, 2003. – 82 с.

Сопротивление материалов. Под ред. А.Ф. Смирнова: Учеб. для вузов. – 3-е изд., перераб. и доп. – М.: Высш. шк., 1975. – 480 с.

Стёпин П.А. Сопротивление материалов: Учеб. для вузов. – 7-е изд. – М.: Высш. шк., 1983. – 303 с.

Шинкин В.Н. Сопротивление материалов. Простые и сложные виды деформаций: Курс лекций. – М.: Издательский Дом МИСиС, 2008. – 307 с.

Источник

Большая Энциклопедия Нефти и Газа

Диаграмма растяжения хрупких материалов показана на рис. 7.23. Здесь не наблюдается площадки текучести и разрушению не предшествует ниспадающая ветвь. Такая диаграмма характерна для чугуна. Ряд пластичных материалов не обладает площадкой текучести и ярко выраженным пределом упругости. [1]

Диаграммы растяжения хрупких материалов значительно отличаются от приведенных выше диаграмм растяжения пластичных материалов. В них осутствует площадка текучести, разрушение образцов происходит при ничтожно малых остаточных деформациях без образования шейки. Хрупкие материалы плохо сопротивляются растяжению. Однако в пределах тех напряжений, при которых хрупкий материал работает в конструкциях на растяжение, указанное отклонение невелико и при расчетах не учитывается. [2]

Диаграмма растяжения хрупких материалов показана на рис. 7.23. Здесь не наблюдается площадки текучести и разрушению не предшествует ниспадающая ветвь. Такая диаграмма характерна для чугуна. Ряд пластичных материалов не обладает площадкой текучести и ярко выраженным пределом упругости. [3]

Диаграмма растяжения хрупких материалов показана на рис. 92, г, где отклонение от закона Гука начинается при малых значениях деформирующей силы. Эта диаграмма не имеет площадки текучести. Образцы разрушаются при очень малой остаточной деформации без образования шейки. За характеристику прочности хрупких материалов, как и в случае растяжения, принимается временное сопротивление. [4]

Диаграмма растяжения хрупких материалов 3 не имеет площади текучести и зоны упрочнения. У таких материалов величина удлинения при разрыве не превышает 2 %, а в ряде случаев измеряется долями процента. К хрупким материалам относятся чугун, высокоуглеродистая сталь. [6]

Диаграмма растяжения хрупкого материала ( рис. 224) значительно отличается от диаграммы для пластичного материала. Площадка текучести отсутствует; разрушение образца происходит при весьма малых остаточных деформациях, без образования шейки. [7]

Диаграмма растяжения хрупкого материала ( рис. 2.25) значительно отличается от диаграммы для пластичного материала: площадка текучести отсутствует; разрушение образца происходит при весьма малых остаточных деформациях, без образования шейки. Основной механической характеристикой является предел прочности. [8]

Диаграммы растяжения хрупких материалов значительно отличаются от приведенной выше диаграммы пластичного материала. В них отсутствует площадка текучести, разрушение образцов происходит при ничтожно малых остаточных деформациях без образования шейки. Хрупкие материалы плохо сопротивляются растяжению. [9]

Материалы, обладающие очень малой пластичностью, называются хрупкими Диаграмма растяжения хрупких материалов не имеет площадки текучести, у них при разрушении не образуется шейка. [10]

Материалы, обладающие очень малой пластичностью, называются хрупкими. Диаграмма растяжения хрупких материалов не имеет площадки текучести, у них при разрушении не образуется шейка. [11]

Материалы, обладающие очень малой пластичностью, называют хрупкими. Диаграмма растяжения хрупких материалов не имеет площадки текучести, у них при разрушении не образуется шейка. [12]

Материалы, обладающие очень малой пластичностью, называются хрупкими. Диаграмма растяжения хрупких материалов не имеет площадки текучести, у них при разрушении не образуется шейка. [13]

Материалы, обладающие очень малой пластичностью, называют хрупкими. Диаграмма растяжения хрупких материалов не имеет площадки текучести, у них при разрушении не образуется шейка. [14]

Источник